Abstract
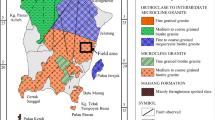
The objective of this paper is to investigate the applicability of artificial neural networks in inverting quasi-3D DC resistivity imaging data. An electrical resistivity imaging survey was carried out along seven parallel lines using a dipole-dipole array to confirm the validation of the results of an inversion using an artificial neural network technique. The model used to produce synthetic data to train the artificial neural network was a homogeneous medium of 100Ωm resistivity with an embedded anomalous body of 1000Ωm resistivity. The network was trained using 21 datasets (comprising 12159 data points) and tested on another 11 synthetic datasets (comprising 6369 data points) and on real field data. Another 24 test datasets (comprising 13896 data points) consisting of different resistivities for the background and the anomalous bodies were used in order to test the interpolation and extrapolation of network properties. Different learning paradigms were tried in the training process of the neural network, with the resilient propagation paradigm being the most efficient. The number of nodes, hidden layers, and efficient values for learning rate and momentum coefficient have been studied. Although a significant correlation between results of the neural network and the conventional robust inversion technique was found, the ANN results show more details of the subsurface structure, and the RMS misfits for the results of the neural network are less than seen with conventional methods. The interpreted results show that the trained network was able to invert quasi-3D electrical resistivity imaging data obtained by dipole-dipole configuration both rapidly and accurately.
Similar content being viewed by others
References
Aristodemou E, Pain C, De Oliveira C, Goddard T and Harris C 2005 Inversion of nuclear well-logging data using neural networks; Geophys. Prospect. 53 103–120.
Battiti R 1992 First and second order methods for learning: Between steepest descent and Newton’s method; Neural Computation 4(2) 141–166.
Baum E and Hausler D 1989 what size net gives valid generalization? In: Advances in Neural Information Processing Systems I (ed.) D. Touretzky, 80–90. Morgan Kaufman.
Claerbout J F and Muir F 1973 Robust modeling with erratic data; Geophysics 38 826–844.
Cranganu C 2007 Using Artificial Neural Networks to predict the presence of overpressured Zones in the Anadarko Basin, Oklahoma; Pure Appl. Geophys. 164 2067–2081.
Dahlin T 1996 2D resistivity surveying for environmental and engineering applications; First Break 14 275–284.
Dahlin T and Loke M H 1997 Quasi-3D resistivity imagingmapping of three dimensional structures using two dimensional DC resistivity techniques; Proceedings of the 3rd Meeting of the Environmental and Engineering Geophysical Society, Aarhus, Denmark, 143–146.
Edwards L S 1977 A modified pseudosection for resistivity and induced-polarization; Geophysics 42 1020–1036.
El-Qady G and Ushijima K 2001 Inversion of DC resistivity data using neural networks; Geophys. Prospect. 49 417–430.
Hagan M T and Menhaj M 1994 Training feed forward networks with the Marquardt algorithms; IEEE Transactions on Neural Networks 5(6) 989–993.
Hagan M T, Demuth H B and Beale M H 1996 Neural Network Design, Boston, MA: PWS Publishing, chapter 10–12.
Irie B and Miyake S 1988 Capabilities of three-layered perceptrons; In: Proceedings of the 1st IEEE International Conference on Neural Networks, SOSPrinting, San Diego, CA 1 (eds) Caudill M and Butler C, 641–648.
Loke M H and Barker R D 1996a Practical techniques for 3D resistivity surveys and data inversion; Geophys. Prospect. 44 499–523.
Loke M H and Barker R D 1996b Rapid least-squares inversion of apparent resistivity Pseudo-sections using quasi-Newton method; Geophys. Prospect. 44 131–152.
Loke M H 2009 Tutorial: 2-D and 3-D electrical imaging surveys. www.geoelectrical.com
Practical Guide to 2D and 3D Surveys. http://www.terrajp.co.jp/lokenote.pdf.
McGillivray P R and Oldenburg D W 1990 Methods for calculating Frechet derivatives and sensitivities for the nonlinear inverse problem: A comparative study; Geophys. Prospect. 38 499–524.
Minsky M L and Papert S A 1969 Perceptron: MIT press.
Mochales T, Casas A M, Pueyo E L, Pueyo O, Roman M T, Pocovi A, Soriano M A and Anson D 2008 Detection of underground cavities by combining gravity, magnetic and ground penetrating radar surveys: A case study from the Zaragoza area, NE Spain; Environ. Geol. 53 1067–1077.
Poulton M and El-Fouly A 1991 Preprocessing GPR signatures for cascading neural network classification; 61st SEG meeting, Houston, USA, Expanded Abstracts 507–509.
Poulton M, Sternberg K and Glass C 1992 Neural network pattern recognition of subsurface EM images; J. Appl. Geophys. 29 21–36.
Powell M J D 1977 Restart procedures for the conjugate gradient method; Math. Program. 12 241–254.
Riedmiller M 1993 Proceedings of the IEEE International Conference on Neural Networks (ICNN), San Francisco 586–591.
Rosenblatt F 1962 Principles of neuro-dynamics: Spartan books.
Scales L E 1985 Introduction to non-linear optimization (New York: Springer-Verlag).
Singh U K, Somvanshi V K, Tiwari R K and Singh S B 2002 Inversion of DC resistivity data using neural network approach; In: Proceedings of the International Groundwater Conference, Dindigul, India, IGC-2002, 57–64.
Singh U K, Tiwari R K and Singh S B 2005 One-dimensional inversion of geoelectrical resistivity sounding data using artificial neural networks — a case study; Comput. Geosci. 31 99–108.
Spichak V V and Popova I V 2000 Artificial neural network inversion of MT — data in terms of 3D earth macro — parameters; Geoph. J. Int. 42 15–26.
Spitzer K 1998 The three-dimensional DC sensitivity for surface and subsurface sources; Geophys. J. Int. 134 736–746.
Thomas G 2004 Inversion Methods and Resolution Analysis for the 2D/3D Reconstruction of Resistivity Structures from DC Measurements. Ph.D thesis, University of Freiberg, pp. 160
Tohon D S, Vannesta K, Sintubin M, Muchez P and Waelkens M 2004 Two-dimensional resistivity imaging: a tool in archaeoseismology: An example from Ancient Sagalassos (Southwest Turkey); Archaeol. Prospect. 11 1–18.
Tsourlos P and Ogilvy R 1999 An algorithm for the 3-D Inversion of Tomographic Resistivity and Induced Polarization data: Preliminary Results; J. Balkan Geophys. Soc. 2(2) 30–45.
Wolke R and Schwetlick H 1988 Iteratively reweighted least squares algorithms, convergence analysis, and numerical comparisons: SIAM Journal of Scientific and Statistical Computations 9 907–921.
Zhao S and Yedlin M J 1996 Some refinements on the finitedifference method for 3-D dc resistivity modeling; Geophysics 61 1301–1307.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Neyamadpour, A., Wan Abdullah, W.A.T. & Taib, S. Inversion of quasi-3D DC resistivity imaging data using artificial neural networks. J Earth Syst Sci 119, 27–40 (2010). https://doi.org/10.1007/s12040-009-0061-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12040-009-0061-2