Skip to main content
SpringerLink
Log in

Bifurcations and new exact travelling wave solutions for the bidirectional wave equations

  • Published:
Pramana Aims and scope Submit manuscript

Abstract

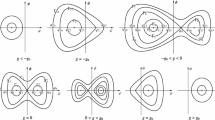
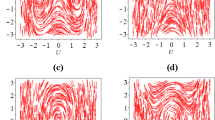
By using the method of dynamical system, the bidirectional wave equations are considered. Based on this method, all kinds of phase portraits of the reduced travelling wave system in the parametric space are given. All possible bounded travelling wave solutions such as dark soliton solutions, bright soliton solutions and periodic travelling wave solutions are obtained. With the aid of Maple software, numerical simulations are conducted for dark soliton solutions, bright soliton solutions and periodic travelling wave solutions to the bidirectional wave equations. The results presented in this paper improve the related previous studies.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Figure 1
Figure 2
Figure 3
Figure 4
Figure 5
Figure 6
Figure 7
Figure 8
Figure 9
Figure 10

Similar content being viewed by others

References

  1. J Lee and R Sakthivel, Pramana – J. Phys. 76, 819 (2011)

    Article  ADS  Google Scholar 

  2. B Anitha, S Rathakrishnan, P Sagayaraj, and A J A Pragasam, Chin. J. Phys. 52, 939 (2014)

    Google Scholar 

  3. C Chun and R Sakthivel, Comput. Phys. Commun. 181, 1021 (2010)

    Article  ADS  MathSciNet  Google Scholar 

  4. R Sakthivel, C Chun, and J Lee, Z. Naturforsch. A 65, 633 (2010)

    ADS  Google Scholar 

  5. J Lee and R Sakthivel, Pramana – J. Phys. 81(6), 893 (2013)

    Article  ADS  Google Scholar 

  6. M Chen, Appl. Math. Lett. 11, 45 (1998)

    Article  Google Scholar 

  7. Jibin Li, Singular nonlinear travelling wave equations: Bifurcations and exact solutions (Science Press, Beijing, 2013)

  8. Jibin Li and Huihui Dai, On the study of singular nonlinear travelling equations: Dynamical system approach (Science Press, Beijing, 2007)

  9. Shaolong Xie, Lin Wang, and Yuzhong Zhang, Commun. Nonlinear Sci. Numer. Simulat. 17, 1130 (2012)

  10. Heng Wang and Shuhua Zheng, Chaos, Solitons and Fractals 82, 83 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  11. P M Byrd and M D Friedmann, Handbook for elliptic integrals for engineers and scientists (Springer, Berlin, 1971)

Download references

Acknowledgements

The authors gratefully acknowledge the support of the National Science Foundation of China under Grant No. 11261049 and the National Science Foundation of China under Grant No. 11161038.

Author information

Authors and Affiliations

  1. College of Global Change and Earth System Science, Beijing Normal University, Beijing, 100875, People’s Republic of China

    HENG WANG

  2. Investment and Development Department, Market and Investment Center, Yunnan Water Investment Co., Limited (06839.HK), Kunming, 650106, People’s Republic of China

    SHUHUA ZHENG

  3. College of Statistics and Mathematics, Yunnan University of Finance and Economics, Kunming, 650221, People’s Republic of China

    LONGWEI CHEN & XIAOCHUN HONG

Authors
  1. HENG WANG
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. SHUHUA ZHENG
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. LONGWEI CHEN
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. XIAOCHUN HONG
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

WANG, H., ZHENG, S., CHEN, L. et al. Bifurcations and new exact travelling wave solutions for the bidirectional wave equations. Pramana - J Phys 87, 77 (2016). https://doi.org/10.1007/s12043-016-1274-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12043-016-1274-y

Keywords

PACS Nos

Search

Navigation