Introduction

The dependence on groundwater has gone up over the years in most of the urban areas due to inadequacy of surface water resources to meet the water requirements. Majority of Indian states are withdrawing groundwater for both agricultural and industrial purposes at a rate more than what can be recharged (Jat et al. 2008). Groundwater problems to a great extent are the consequence of human activities like uncontrolled withdrawal of borewell water at a high rate compared to recharge rate (Kazi et al. 2009). In any area, the characteristics of groundwater are due to natural and anthropogenic processes, which have the capability to alter these systems by contaminating them or modifying the hydrological cycle (Helena et al. 2000; Kumar et al. 2017). When pollution of groundwater in aquifers happens, it perseveres for a long time as a result of slow movement of water in them. The harmful impacts of rural and modern exercises and urban advancement on adjoining groundwater have incited examinations on the nature of these sources (Dawoud and Raouf 2009). It is consequently desirable to ensure that groundwater quality is secured for its utilization in different purposes (Jammel and Hussain 2003; Tirkey et al. 2017). To protect groundwater quality for drinking, periodical monitoring of its quality is essential in urban regions. But testing of different water quality parameters is costly, takes lot of time and is a tedious process. Also measurement of all the parameters at a consistent interim is not required since this will not give extra data on the water quality aspect (Mustapha and Aris 2012a). In order to aid the administration to prioritize and to make informed decisions so as to improve the groundwater quality, it is very important to reduce the apprehensions involved in the dataset by interpreting the spatial and temporal variations in water quality (Wang et al. 2008) and also to locate hidden pollution sources (Zhang et al. 2009).

In recent years, few data-driven approaches like the projection pursuit technique and neural networks have been used for assessing the water quality (Salman and Ruka’h 1999). Water Quality Index (WQI) is regarded as one of the most effective way to communicate water quality (Sadat-Noori et al. 2014). Horton (1965) suggested that various water quality data could be aggregated into an overall index. However, multivariate statistical techniques can be employed for analyzing huge water quality datasets with minimal loss of important information (Juahir et al. 2011; Samson and Elangovan 2017; Shrestha and Kazama 2007). Multivariate statistical techniques, such as cluster analysis (CA), principal component analysis (PCA), factor analysis (FA) and discriminant analysis (DA) can interpret complex data matrices for improved understanding of water quality and other environmental systems by allowing the identification of possible factors/sources thus serving as a worthy tool for quickly solving pollution problems (Vega et al. 1998; Lee et al. 2001; Wunderlin et al. 2001; Reghunath et al. 2002; Simeonov et al. 2003, 2004; Ravikumar and Somashekar 2017). Principal component analysis (PCA) has been utilized to take out the noise from huge data matrix and classify the variables into measurable components, discriminant analysis (DA) recognizes the most segregating measurable element/variable according to goodness and cluster analysis (CA) chooses the identical group inside a specific data set. Characterization and evaluation of surface and freshwater quality performed by multivariate statistical techniques has proved to be useful in verifying spatial and temporal variations caused naturally and due to human induced factors also (Helena et al. 2000; Singh et al. 2004, 2005; Hassen et al. 2016).

Bengaluru has suddenly overgrown its size after the Information Technology boom. Consequent to this the city and the district administration is struggling to provide necessary infrastructure. The demand for water supply in particular requires scientific planning and effective management of water resources, especially the groundwater in the district (CGWB 2012). In this study, groundwater quality data measured during pre and post monsoon on 14 parameters from 67 sites distributed across the western half of the Bengaluru city were subjected to different multivariate statistical approaches (CA, DA, PCA/FA) in order to evaluate the temporal and spatial variations in groundwater quality caused by parameters and to recognize the likely factors causing variation in groundwater quality.

Materials and methods

Study area

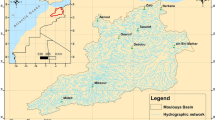
The study area (Fig. 1) is situated in the northwestern and southwestern corner of Bengaluru city, between 12°48′24.52″ and 12°53′59.85″ North latitude and 77°24′59.95″ to 77°30′6.72″ East Longitude and spreads over a region of 241 km2. It gets precipitation from both upper east and the southwest storms with yearly aggregate precipitation of around 900 mm. Bengaluru city is for the most part depleted by part of the Arkavathi river catchment toward the west and South Pennar river toward the east. The versatility, presence and aquifer refill of groundwater event are dominated by the measure of weathering, fracture pattern, geomorphological setup and rainfall. The Bangalore urban district contains crystalline storm cellar, fundamentally gneisses and rocks meddled by essential dykes. These arrangements have been modified to laterite along the eastern edge of the city. The city is intensely reliant on groundwater for its household and commercial needs. The appraisal of groundwater asset demonstrates that the asset is over misused. As a result of this overuse, groundwater quality has additionally disintegrated (DMG 2003, 2011).

Fig. 1
figure 1

Location map of the study area

Full size image

Hydrogeology

Granites and Gneisses of peninsular gneissic group form the primary aquifers in the study region. Laterites of tertiary age occur as isolated patches capping crystalline rocks. Alluvium of limited thickness and aerial extent 20–25 m thick occur along the river courses possessing substantial groundwater potential. Groundwater occurs in phreatic conditions or unconfined conditions in the weathered zone and under semi-confined to confined conditions in fractured and jointed rock formations. Groundwater movement and recharge of aquifers are controlled by various factors like fracture pattern, degree of weathering, geo-morphological setup and amount of rainfall received. The resistivity examinations uncovered the presence of an exceedingly weathered rock (permeable) reaching out up to a depth of 30 m. The principal aquifer exists between 25 and 30 m depth. There are aquifers even past 60 m depth. The area is sloping towards west. Streams of various watersheds start from this area. Significant piece of the study zone is possessed by streams streaming towards west from this region (DMG 2011; CGWB 2012).

Monitored parameters

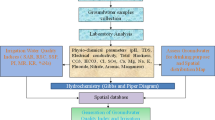
A total of 67 groundwater samples were collected in the month of March (2014) for pre-monsoon and November (2014) for post-monsoon seasons. The sampling locations were selected with a view to cover residential, industrial and commercial areas so as to achieve a good sampling representation over the study area. The samples were collected from bore wells after 10 min of pumping in pre-cleaned sterilized plastic bottles and stored in an ice box. The samples collected were analyzed for 14 physico-chemical parameters, namely pH, total dissolved solids (TDS), electrical conductivity (EC), nitrate (NO3−), chloride (Cl–), sulfate (SO42−) magnesium (Mg2+), sodium (Na+), calcium (Ca2+), potassium (K+), iron (Fe), alkalinity (HCO ⎯3 ), total hardness(TH) and fluoride (F–). Electrical conductivity and pH were measured in the field immediately after sampling and the remaining parameters were determined in laboratory within 24 h.

Analysis methods

The sampling, preservation, transportation and analysis of water samples were performed according to standard methods (APHA 2005). The analytical data quality was ensured through careful standardization, procedural blank measurements and spiked and duplicate samples. Calcium and magnesium were determined by EDTA titrations method, sodium and potassium by flame emission photometry, iron by phenanthroline spectrophotometry, bicarbonate and carbonate by titrimetry, chloride by argnetometric titration, nitrate by UV spectrometry, sulfate by nephelometry, total dissolved solids by gravimetry, total hardness by potentiometry and flouride by ion selection electrode method. pH and electrical conductivity were measured in situ using digital portable water analyser (Systronics –371). pH meter was calibrated by immersing the probe using two standard solutions (pH 4 and 10 buffers) while electrical conductivity meter was calibrated by immersing the probe in standard KCl solution (0.1 N). The accuracy of the chemical analysis was verified by calculating ion-balance errors using Aquachem, where the errors were generally around 5%.

Data pretreatment

The statistical analysis of data was carried out using SPSS software, v 20.0. The methods, such as CA and FA, require variables to conform to a normal distribution. Normal distribution of data is an essential requirement for multivariate statistical analyses because the analyses will be valid only if the standard deviations (variances) are low (very close to 0). Else, the parameters with the highest variances will influence the analysis (Güler et al. 2002; Cloutier et al. 2008; Yidana et al. 2011; Boateng et al. 2016). The raw data indicated that Ca, Na, HCO3− and SO42− were very close to normal distribution, but the distribution pattern of other parameters was not normal. Hence these parameters were log transformed to make the data to have normal distribution (Zhang et al. 2009). The standard z-scores of all the parameters were then used for the multivariate statistical analysis to lessen the effects of differences in the units used for measurement and variance and to render the data dimensionless (Singh et al. 2005; Yidana et al. 2011). The z scores were calculated as in Eq. (1):

$$z = \frac{{x - { \bar{x} } }}{s},$$
(1)

where x represents the value, \({ \bar{x}}\)represents the mean and s represents the standard deviation of the parameter, at a given sampling site.

Water quality index (WQI)

A WQI is a single number (like a grade) that expresses overall water quality at a certain location and time based on several water quality parameters. The main purpose of WQI is to turn complex water quality data into information that is understandable and usable by the public. WQI is a single unit less number of 100-point scale that provides a pointer to the quality of water source (Pradhan et al. 2001; Pius et al. 2012). According to this water quality index, the maximum permissible value is 100. Values greater than 100 indicate pollution and are unfit for human consumption. The methodology considered for development of the WQI is adopted from Tiwari and Mishra (1985) as in Eq. (2):

$${\text{WQI}} = {\text{Anti log}}\left[ {\mathop \sum \nolimits {\text{W}}_{{{\text{n}} = 1}}^{\text{n}} \log_{10} qn} \right],$$
(2)

where weightage factor (W) is computed using Wn = K/Sn and K is proportionality constant derived from Eq. (3):

$${\text{K}} = \left[ {{1 \mathord{\left/ {\vphantom {1 {\mathop \sum \limits_{n = 1}^{n} 1/{\text{si}}}}} \right. \kern-0pt} {\mathop \sum \limits_{n = 1}^{n} 1/{\text{si}}}}} \right],$$
(3)

where Sn and Si are the WHO/ICMR standard values of the water quality parameter. Quality rating (q) is calculated using qni = {[(Vactual − Videal)/(Vstandard − Videal)] × 100},where qni = quality rating of ith parameter for a total of n water quality parameters, Vactual = value of the water quality parameter obtained from laboratory analysis, Videal = value of water quality parameter that can be obtained from the standard tables, Videal for pH 7 and for other parameters is equivalent to zero, Vstandard = WHO/ICMR standard of the water quality parameter. Based on the above WQI values, the ground water quality is rated as excellent, good, poor, very poor and unfit for human consumption (Table 3).

Cluster analysis (CA)

CA is one of the multivariate techniques, which groups the objects based on their characteristics. It arranges the objects, such that every object is same as the others in the cluster according to a predefined selection criterion. The clusters of objects obtained should then display high internal (within-cluster) resemblance and high external (between clusters) diversity. Hierarchical agglomerative clustering is the most commonly used approach (Massart and Kaufman 1983), which supplies with instinctive similarity relationships between any one sample and the entire data set. It is represented by a dendrogram (tree diagram) (McKenna 2003). The dendrogram displays a visual summary of the clustering processes, presenting a picture of the groups and their proximity, with a reasonable lessening in dimensionality of the original data. The Euclidean distance shows the similarity between two samples and a distance can be represented by the difference between analytical values from the samples (Forina et al. 2002; Taoufik et al. 2017).

Using Ward’s method on the normalized data set, hierarchical agglomerative cluster analysis was conducted in this study. To measure the similarity squared euclidean distance was used. The ward’s method makes use of an analysis of variance approach for evaluating the distances between clusters, in order to minimize the sum of squares (SS) of any two clusters that can be formed at each step (Willet 1987; Adams 1998; Otto 1998: Tziritis et al. 2016). Using the linkage distance, the spatial variability of groundwater quality for the study area was determined from cluster analysis, which is reported as Dlink/Dmax. Dlink/Dmax represents the quotient between the linkage distances for a particular case divided by the maximal linkage distance. To standardize the linkage distance, which is represented on the y-axis, the quotient is then multiplied by 100 (Simeonov et al. 2003; Singh et al. 2005).

Discriminant analysis (DA)

DA is a supervised pattern recognition technique, which is used for the classification of objects or cases into exhaustive and mutually exclusive groups based on a set of independent variables. It is a suitable statistical technique when the dependent variable is a categorical variable and the independent variables are metric (Mustapha and Aris 2012). The purpose of DA is to increase the similarity between-group relative to the within-group variance. DA finds out the variables that discriminate between two or more expected occurring groups (Johnson and Wichern 1992). It also forms a discriminant function (DF) for each group as in Eq. (4):

$$f(G_{i} ) = k_{i} + \mathop \sum \limits_{j = 1}^{n} w_{ij} p_{ij} ,$$
(4)

where i is the number of groups (G), k i the constant inherent to each group, n the number of parameters used to classify a set of data into a given group, w j the weight coefficient, assigned by DA to a given selected parameter (p j ).

In the present study, DA was carried out on raw data using three different modes: standard, forward stepwise and backward stepwise to construct discriminant functions (DFs) and to assess both temporal and spatial variations in groundwater quality. Temporal DA was done taking the monitoring period (pre-monsoon and post-monsoon) as the grouping variable and the 14 measured groundwater quality parameters as the independent variables. Spatial DA was done in the same way as temporal DA, by taking the spatial clusters obtained in cluster analysis as the grouping variable and the 14 measured water quality parameters as the independent variables.

Principal component analysis/factor analysis

PCA is a technique, which converts the original variables into new uncorrelated variables (axes), known as principal components, which are linear combinations of the original variables (Sarbu and Pop 2005). The new axes lie in the directions where variance is maximum (Hossain et al. 2015). PCA supplies the details of most significant parameters, which describes the whole data set thereby reducing the data with minimal loss of original information (Helena et al. 2000). The principal component (PC) can be expressed as in Eq. (5):

$$z_{ij} = a_{i1} x_{1j} + a_{i2} x_{2j} + a_{i3} x_{3j} + \cdots + a_{im} x_{mj} ,$$
(5)

where a is the component loading, z the component score, x the measured value of a variable, I the component number, j the sample number and m the total number of variables.

PCA is continued with factor analysis. The objective of factor analysis is to lessen the inputs from unimportant variables in order to further simplify the data structure obtained from PCA (Aris et al. 2012; Noshadi and Ghafourian 2016). This objective can be accomplished by rotating the axis defined by PCA, according to well-established rules, and generating new variables, called varifactors (VF). A principal component is a linear combination of observable water quality variables, whereas varifactor can include unobservable, hypothetical, latent variables (Vega et al. 1998; Helena et al. 2000; Qian et al. 2016). PCA of the normalized variables was carried out to extract significant principal components and to further reduce the contribution of less significant variables. Then the extracted principal components were subjected to varimax rotation (raw) generating varifactors (Brumelis et al. 2000; Love et al. 2004; Abdul-Wahab et al. 2005). As a result, a small number of factors will usually account for approximately the same amount of information as do the much larger set of original observations. In FA, the basic concept is expressed as in Eq. (6):

$$z_{ji} = a_{f1} f_{1i} + a_{f2} f_{2i} + a_{f3} f_{3i} + \cdots + a_{\text{fm}} f_{\text{mi}} + e_{\text{fi}} ,$$
(6)

where z is the measured value of a variable, a the factor loading, f the factor score, e the residual term accounting for errors or other sources of variation, i the sample number, j the variable number and m the total number of factors.

Results and discussion

Groundwater chemistry

Basic statistics of the respective values for all the physico-chemical parameters in the pre and post-monsoon groundwater samples from the study area and corresponding permissible limits as specified by the Bureau of Indian Standards (2012) are presented in Table 1 and as box plot in Fig. 2a–c. The values of pH in groundwater of study area vary from 6.07 to 8.13 in pre-monsoon and 5.8 to 7.7 in post-monsoon, indicating slightly acidic to alkaline nature. This shows that there is little seasonal fluctuation in pH values in the area that islower than the permissible limit of 6.5⎯8.5. The electrical conductivity of groundwater varies widely, ranging from 240 to 4230 μS/cm in pre-monsoon and 254 to 4483 μS/cm in post-monsoon. The total dissolved solids values varied between 152 and 2242 mg/L in pre-monsoon and 162 and 2869 mg/L in post-monsoon. The electrical conductivity and total dissolved solids values in all the samples were well above their respective desirable limits of 1400 μS/cm and 500 mg/L indicating the presence and dissolution of higher salt content.

Table 1 Basic statistics of groundwater quality data of the study region
Full size table
Fig. 2
figure 2figure 2figure 2

a Box plots of groundwater quality parameters Ca, Mg, Na, K, Fe, HCO3. b Box plots of groundwater quality parameters Cl, Fe, NO3, SO4, TDS, EC. c Box plots of groundwater quality parameters TH, pH, F

Full size image

Water hardness is caused primarily by the presence of cations, such as calcium and magnesium and anions, such as carbonate, bicarbonate, chloride and sulfates in water. Water hardness varied between 48 and 1784 mg/L for the pre-monsoon period and 50 and 1873 mg/L during post-monsoon period thereby exceeding the desirable limit of 300 mg/L in many samples. Among the alkaline earths, the concentration of calcium is in the range of 6–312 mg/L in pre-monsoon and 6–316 mg/L in post-monsoon, while magnesium content ranges between 8–3244 mg/L in pre-monsoon and 8–268 mg/L in post-monsoon seasons, their higher concentrations indicating hardness in groundwater. Bicarbonate is the predominant anion in both pre and post-monsoon seasons, whose concentration varied from 88 to 505 mg/L in pre-monsoon and 92 to 530 mg/L in post-monsoon. Higher concentration of bicarbonate may be attributed to leaching of mineral substances in the soil and atmosphere during natural filtration of water from sewage (Ravikumar et al. 2012).

Chlorides are in the range of 19–607 mg/L and 20–667 mg/L, respectively, during pre-monsoon and post-monsoon, indicating that there is not much difference in chloride concentration between seasons. Presence of chloride in the groundwater of the study area is due to seepage from sewers, septic tanks and industrial effluents. The nitrate concentration in the study area ranges from 2 to 252 mg/L in pre-monsoon and 2 to 262 mg/L in post-monsoon seasons. Majority of the samples among pre-monsoon samples showed nitrate concentration above the permissible limit of 45 mg/L, which can be attributed to contamination from septic tank and sewage effluent as there is no agricultural activity nor application of nitrogenous fertilizers as it is an urban area. Further, the fluoride concentration was found to vary from 0.11 to 1.38 mg/L in pre-monsoon and 0.11 to 1.40 in post-monsoon, which is exceeding the desirable limit of 1 mg/L in the study area. The geology of the study area is predominated by granites/gneisses with intensive presence of pegmatites, which contributes to the occurrence of fluoride in bore wells.

Estimation of water quality index

In the present study, 12 water quality parameters, pH, TDS, Hardness, F, Fe, Na, SO4, NO3, Cl, Na, Ca, Mg were considered for computing WQI. It is well known that the more harmful a given pollutant is, the smaller is its permissible value for the standard recommended for drinking water. So, the “weights” for various water quality parameters are assumed to be inversely proportional to the recommended standards for the corresponding parameters (Pius et al. 2012). Calculated relative weight (Wi) values of each parameter are given in Table 2.

Table 2 Water quality parameters, their standards and unit weights
Full size table

Water quality types were determined on the basis of WQI. The computed WQI values range from 19 to 145 and 24 to 164 for pre-monsoon and post-monsoon, respectively. The WQI range, type of water and calculation of WQI for percentage samples are classified in Table 3. It can be observed that out of 67 groundwater quality data points 24 stations (35%) fall in the “excellent” category, 16 stations (23%) in “good” category, 18 stations (26%) in “poor” category, 7 stations (10%) in “very poor” category and 3 stations (4%) in unfit category for pre-monsoon season. During post-monsoon, 20 stations (30%) fall in the “excellent” category, 16 stations (23%) in “good” category, 16 stations (23%) in “poor” category 9 stations (13%) in “very poor” category and 5 stations (7%) in unfit category for post-monsoon dataset. The post-monsoon samples show signs of poor quality in drinking purpose compared to pre-monsoon. Rainfall data published by Indian Meteorology Department (IMD) revealed that Bangalore region received comparatively higher pre-monsoon rainfall and normal monsoon rainfall while the rainfall in the post-monsoon season was about 31% deficient, when the data were collected. Thus the dilution effect of rainfall recharge is observed to be higher in the pre-monsoon season. Also, when the rainfall is deficient, there is a risk of higher concentration of surface pollutants getting infiltrated into the groundwater.

Table 3 The WQI range, type of water and percentage wise water quality index area distribution
Full size table

Spatial similarity and site grouping

CA for pre-monsoon and post-monsoon data provided a dendrogram grouping the 67 sampling sites into two statistically important clusters (cluster 1 and cluster 2), containing 36 and 31 sites for cluster 1 and 34 and 33 sites for cluster 2, respectively, at (Dlink/Dmax) × 100 < 25 as shown in Fig. 3a, b. From the cluster characteristics given in Table 4 it was observed that, for both pre-monsoon and post-monsoon data, the classification of sampling sites in cluster 1 showed higher level of pollution as compared to cluster 2. While the parameter concentrations in cluster 2 are comparatively lower, some parameters still exceeded the desirable limits. Thus cluster 1 represents high pollution sites and cluster 2 represents low pollution sites. It can be seen that the CA technique is helpful in giving out valid classification of groundwater in the entire region. This will help in designing a future spatial sampling strategy in an optimal manner reducing the number of sampling sites in the monitoring network, which will reduce the cost without affecting the significance of the outcome.

Fig. 3
figure 3

Dendrogram showing sampling site clusters for a pre-monsoon data and b post-monsoon data

Full size image
Table 4 Cluster characteristics
Full size table

Spatial and temporal variations in groundwater quality

Discriminant analysis was used in order to identify the most important parameters influencing the spatial and temporal variations in groundwater quality. Only 12 parameters were considered for DA excluding TDS and EC to avoid multicollinearity. Discriminant functions (DFs) and classification matrices (CMs) were derived from the standard, forward stepwise and backward stepwise modes of DA. Temporal DA was performed on raw data taking season (pre-monsoon and post-monsoon) as the grouping variable and the measured parameters as the independent variables. The classification functions obtained are given in Table 5 and the classification matrix is given in Table 6.

Table 5 Classification functions for temporal DA
Full size table
Table 6 Classification matrix for temporal DA
Full size table

Standard mode DA constructed DFs using all 12 parameters to give 76% correct assignation of cases in the CM. The forward stepwise mode used only six parameters (K, Fe, HCO3, NO3, pH and F) giving 74% correct assignation and the backward stepwise mode gave 72% correct assignation of cases using only one parameter (pH). Thus temporal DA indicated that pH is the most important parameter, which discriminates between the water quality in the pre-monsoon and post-monsoon seasons, followed by K, Fe, HCO3, NO3 and F.

Spatial DA was performed on raw data taking cluster (1 and 2) as the grouping variable and the measured parameters as the independent variables. The classification functions obtained are given in Table 7 and the classification matrix is given in Table 8. Standard mode DA constructed DFs using all 12 parameters to give 91% correct assignation of cases in the CM. The forward stepwise mode used seven parameters (Mg, K, HCO3, Cl, NO3, SO4 and F) giving 90% correct assignation and the backward stepwise mode gave 89% correct assignation of cases using only three parameters (Mg, Cl and NO3). Thus spatial DA identified Mg, Cl and NO3 as the three most important parameters, which cause the discrimination between the two clusters, followed by K, HCO3, SO4 and F.

Table 7 Classification functions for spatial DA
Full size table
Table 8 Classification matrix for spatial DA
Full size table

Data structure determination and source identification

Principal component analysis was applied to standardized datasets separately for the two clusters delineated by CA in order to identify and compare the factors influencing the high and low pollution clusters. Before carrying out PCA, the Kaiser–Meyer–Olkin (KMO) and Bartlett’s sphericity tests were performed on the parameter correlation matrix in order to examine the validity of the PCA (Mustapha et al. 2012). For cluster 1, KMO value of 0.697 > 0.6 and Bartlett’s Sphericity test significance p < 0.05 confirmed suitability for PCA. The parameters K, NO3, Fe and pH were excluded from the analysis due to communalities < 0.5. PCA with varimax rotation was applied to the standardized datasets of the remaining ten parameters. For cluster 2, KMO value of 0.691 > 0.6 and Bartlett’s Sphericity test significance p < 0.05 confirmed suitability for PCA. The parameters K, NO3, Fe and pH were excluded from the analysis due to communalities < 0.5. PCA with varimax rotation was applied to the standardized datasets of the remaining ten parameters.

PCA of the high and low pollution cluster datasets (cluster 1 and cluster 2) yielded three PCs for both the high and low pollution sites with eigenvalues greater than 1, explaining 85 and 84% of the total variance in the respective groundwater quality data sets. Eigenvalue is important in measuring the significance of the factor, i,e factors with the greater eigenvalues are considered to be most significant. Eigenvalues of 1.0 or greater are considered significant (Kim and Mueller 1987). Same number of VFs were obtained for two clusters by performing FA on the PCs. Variable loadings, explaining variance and corresponding VFs, are presented in Table 9. (Liu et al. 2003) designated the factor loadings as ‘weak’, ‘moderate’ and ‘strong’, with respect to the absolute loading values of 0.50–0.30, 0.75–0.50 and > 0.75, respectively.

Table 9 Varimax rotated factor loading on significant PCs of cluster 1 and cluster 2
Full size table

For the data set pertaining to cluster 1, VF1, which explained 47.4% of the total variance had strong positive loadings on Ca, Mg, TDS, EC and TH and moderate positive loading on Na. Thus VF1 mainly accounts for calcium and magnesium salts in water resulting in high hardness. Also it can be inferred that the high electrical conductivity and high dissolved solids’ content in the water samples are predominantly contributed by calcium and magnesium and to a lesser extent by sodium. VF2 explaining 20.9% of the total variance had strong positive loadings on Cl, Na and SO4. Thus VF2 indicates Na–Cl water type and also the presence of sodium sulfate in groundwater. VF3 explaining 17.1% of the total variance had strong positive loadings on HCO3 and F, moderate positive loading on Na and moderate negative loading on SO4. The strong positive loading on F and HCO3 indicates that dissolution of fluoride occurring in groundwater is favorable in alkaline environment.

For the data set representing cluster 2, among the three VFs, VF1, which explained 46.3% of the total variance had strong positive loadings on Ca, Cl, TDS, EC and TH; and moderate positive loadings on Mg and HCO3. Thus VF1 indicates that the presence of high hardness, electrical conductivity and dissolved solids in the groundwater is mainly due to the presence of calcium chlorides and bicarbonates and to a lesser extent due to magnesium chlorides and bicarbonates. VF2 explaining 23.3% of the total variance had strong positive loading on F, HCO3 and SO4; and moderate positive loadings on EC, TDS and Mg. Thus PC2 indicates higher dissolution of Flouride in alkaline environment. Also, the presence of sodium and magnesium sulfates is indicated. PC3 explaining 14.5% of the total variance had strong positive loading on Na and strong negative loading on Mg. Thus PC3 indicates salinity due to sodium ion possibly from sodium-containing rock formations. Also the low loading on HCO3 along with the negative loading on Mg may be due to removal of Mg from the groundwater in the form of Magnesium bicarbonate precipitate.

Conclusions

  • The present study demonstrated the importance of multivariate statistical analysis in groundwater studies. Basic statistics showed that most of the parameters were found to exceed the specified desirable limits while few parameters exceeded the permissible limits as well. The WQI calculated showed that the number of samples rated as poor, very poor and unfit constitute about 50% of the total samples thereby pointing out to the fact that the groundwater of these needs some degree of treatment before consumption, and it also needs to be protected from the perils of contamination. The results of WQI agree with the fact that many parameters exceeded the desirable limits as observed from basic statistical analysis.

  • Different multivariate statistical techniques were applied to evaluate spatial and temporal variations in groundwater quality of Bengaluru city. Hierarchical cluster analysis was useful in classifying the 67 sampling sites into two main clusters as high- and low-pollution areas. This helps in the identification of problematic zones in the area where remedial actions need to be focused. Also, grouping the areas having similar groundwater condition may be used to determine the number of sampling sites required for regular monitoring of groundwater quality.

  • DA was useful in identifying a few indicator parameters responsible for significant variations (spatial and temporal) in groundwater quality of the study area. pH was identified as the most important parameter, which discriminates between the groundwater quality in the pre-monsoon and post-monsoon seasons and accounts for 72% seasonal assignation of cases. Mg, Cl and NO3 were identified as the three most important parameters discriminating between the two clusters and accounting for 89% spatial assignation of cases.

  • Grouping of the measured parameters to identify the underlying factors or processes influencing the groundwater quality in the study region was achieved through PCA. Three principal components (PCs) each were identified for the two clusters. Dissolution of hardness causing Ca and Mg from bed rock and anthropogenic sources, fluoride dissolution from bedrock in alkaline environment and salinity from natural and anthropogenic sources were identified to be the main factors influencing the ground water quality in both the clusters.

  • Thus, the usefulness of multivariate statistical techniques for analysis and interpretation of complex data sets was illustrated in this study for groundwater quality assessment. The grouping information extracted from cluster analysis can be used to design optimal sampling strategy, which; could reduce the number of sampling stations and associated costs. DA provided with data reduction, by identifying the most important parameters, which; needs to be monitored in order to study the spatial and temporal variations in water quality. While PCA served as a means to identify those parameters, which; have greatest contribution to temporal variation in the groundwater quality and suggested possible sets of pollution sources. Overall the multivariate statistical techniques helped in understanding the temporal/spatial variations in groundwater quality, identification of pollution sources/factors as an effort towards a more effective groundwater quality management.