Introduction

Weather, climate and global water cycle have a fundamental relation. The precise prediction of stream flow is greatly influenced by the quality of input weather data for hydrology models (Duncan et al. 1993; Fekete et al. 2004). However, for numerous regions, like vast snow clad areas of Himalaya, which is at high altitude, uneven and inaccessible, there is a scanty distribution of weather stations and excellence of historical measurement is questionable. So there is a challenge of finding proper data for hydrological modeling. According to Konig et al. (2001) in recent decade, remote sensing through satellite has been used over remote areas for studying various processes related to hydrology because of its large contiguous coverage. Gridded data give global coverage compared to traditional ground observation data as well as freely accessible for scientific research and used for those regions where standard in place measurement is not possible just as the Himalayas Region. According to Berezowski et al. (2015), the finer-resolution regional datasets are better fitted for hydrological modeling than the global dataset having coarser resolution. The reanalysis data with higher spatial and temporal scale provide large assemble of climate variable including global extent over several decades (Rienecker et al. 2011; Mesinger et al. 2006). There is an inconsistency of observational network compared to constant assimilation scheme. Moreover, reanalysis data have a significant prospect for hydrology modeling (Choi et al. 2007; Fuka et al. 2013; Vu et al. 2012). Siam et al. 2013 used reanalysis datasets for simulating hydrology models to regenerate observed stream flow and prove the most exact process to examine how the hydrological simulations done by reanalysis forecast models. In high-altitude areas of Indus basins, gridded datasets use only a few station data having commonly available old observatories which don’t exhibit the topographic and contiguous variance of precipitation in those areas (Reggiani and Rientjes 2015). Tanaka and Kotsuki (2013) discussed estimation of Southeast Asia runoff using four precipitation datasets. Getirana et al. (2011) performed a research in Negro River Basin, Amazon, using different precipitation datasets including reanalysis data. For distributed earth system modeling, i.e., hydrology modeling, the high-resolution rainfall and temperature data are becoming highly demanded day by day. In case of rainfall–runoff models, e.g., ARCSWAT, WetSpa and TOPMODEL, precipitation can be used as (Arnold et al. 1998; Beven 1995; Liu and Smedt 2004) an important factor for hydrological processes (Berezowski et al. 2016). Vu et al. (2012) used ARCSWAT model for comparison of output using rainfall data from five different sources at Vietnam river basin and found that gridded dataset can capture hydrological responses in this basin perfectly. At a recent time, a lumped hydrology model was calibrated using weather data from CFSR, NARR, MERRA, ERA-Interim reanalysis and gridded observation database to estimate the stream flow in the continental USA. The study reveals that the performance of NARR forcing is better than gridded observations (Essou et al. 2016). The main focus of the study is to assess the impacts of ERA-Interim global climatic reanalysis data and gridded IMD dataset on ARCSWAT hydrological model simulation. The study also investigates the vigorous changes in extreme weather condition based on ERA-Interim reanalysis and gridded observation dataset (IMD gridded data). The research was conducted at Beas river basin to estimate snowmelt runoff and sediment yield at Pong dam. In catchments with less available data, the adequacy of the study is to validate the use of reanalysis dataset depending on high spatial variation of precipitation and temperature. The study evaluates the possible influence of climate change on stream flow and sediment yield of Beas river basin up to Pong dam using Geographical Information System and hydrological modeling tool. Spatial input data layers needed to run the model are weather data, digital elevation model (DEM), land use data and soil data. The DEM available from Advanced Spaceborne Thermal Emission and Reflection Radiometer Japanese sensor developed by joint operation by NASA and Japan’s Ministry of Economy is used for delineating the boundary and analyzing the drainage patterns of the watershed. Channel slope, slope length, stream length and stream width are derived from DEM. And National Bureau of Soil Survey and Land Use Planning (NBSS&LUP) at 1:250000 is used for deriving soil property. Model calibration was performed by SUFI-2 against observed data obtained by many gauging stations having potential to examine a considerable number of parameters. The IMD meteorological data of 1° × 1° are obtained by interpolating as ground inspections-based gridded data. Dee et al. (2011) first described configuration of reanalysis data ERA-Interim. The climate variables extracted from ERA-Interim are surface air temperature, precipitation, wind speed at 10 m, surface downwelling solar irradiance and relative humidity data. Depending on the variable, the temporal resolution of ERA-Interim is either 3 h (forecast) or 6 h (analysis) (Dee et al. 2011).

Study area

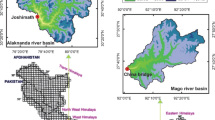
The area selected for the study is the Beas basin (up to Pong dam) that lies in the northwestern part of the Indian Himalayan Region (Fig. 1). The study area covers four districts of Himachal Pradesh, namely Kullu, Mandi, Kangra and Hamirpur (Lakhera et al. 2016). It has an elevation of 4361 m (14308 ft) and is situated at geographical coordinates 32°21′59″–31°16′09″N latitude and 77°05′08″E–74°58′31″E. Beas is a main tributary of Sutlej river, a perennial river originates from southern face of Rohtang Pass in Kullu district and flows about 470 km to join Satluj river in the state of Punjab (256 km up to Pong dam).

Fig. 1
figure 1

Study area of Beas river basin

Full size image

The Beas River is mainly fed by snowmelt during summer. Some major tributaries of the river are Tirthan, Parvati and Sainj rivers near Sabarimala (near Kullu), Larji and Bakhil Khad (near Pandoh dam). During winter, a considerable portion of river becomes snow-covered. The biggest glacier of this basin is Parvati glacier. The altitude of the basin varies from 802 m (near Pandoh dam) up to 6600 m (on Northwest Border) (Lakhera et al. 2016). The catchment area of Beas River is about 20,303 km2 out of which only 777 km2 is under permanent snow and glaciers (http://india-wris.nrsc.gov.in).

Data and methodology

Data used

The fundamental information required for modeling is a Soil and Water Assessment Tool (SWAT) model that includes digital elevation model (DEM) data, land cover data, soil data, hydrological data and meteorological data. For the study area, the datasets used are basin, elevation and slope derived from Aster DEM at 30-m resolution (Fig. 2a, b). Land use land cover data were obtained from NOAA-AVHRR, global 1 km land cover product (Fig. 2c). Soil data were obtained from National Bureau of Soil Survey and Land Use Planning (NBSS&LUP) at 1:250,000 scale (Fig. 2d) (Aggarwal et al. 2016). The vegetation classes for this study area obtained from AVHRR global 1 km land cover product are water, snow, grassland, orchards/vineyards, deciduous forest, evergreen forest, cropland and shrubland.

Fig. 2
figure 2

a DEM map, b slope map, c LULC map and d soil map of Beas basin

Full size image

Land cover classes are converted to their equivalent SWAT LULC classes (Table 1) to be compatible with the model’s LULC data input requirement. However, soil texture information from NBSS&LUP is used to generate the soil parameter. According to USDA taxonomy, viz. Typic Dystrudepts, Typic Cryopsamments, Typic Udorthents, rock outcrops, water bodies, and glaciers and rock outcrops, soil is classified into different categories.

Table 1 SWAT LULC classes corresponding to LULC classes from NOAA-AVHRR
Full size table

Elevation band parameters for SWAT model obtained from DEM (Fig. 3). ARCSWAT allow elevation band up to ten in each subbasin.

Fig. 3
figure 3

Elevation zone map of the basin

Full size image

The meteorological data used for the study are IMD dataset produced by the Indian Meteorological Department for the whole India from 1951 to 2007. Shepard method was used to interpolate the data from weather stations (Shepard 1968). The climate variables acquired from IMD weather data are maximum temperature, minimum temperature, rainfall, relative humidity and solar radiation. The spatial resolution for maximum, minimum temperature and solar radiation obtained from IMD is 1° × 1°. The maximum and minimum temperatures of IMD weather data vary from 11.5 to 35.5 °C and 2 to 25.5 °C from 1990 to 1996, and for ERA-Interim the values are 5–31 °C and − 12 to 22 °C, respectively.

The ERA-Interim (Dee et al. 2011) datasets are of high spatial and temporal resolution with multiple climate variables. The ERA-Interim produced by the ECMWF (European Centre for Medium-Range Weather Forecasts) is atmospheric reanalysis data available globally (Dee et al. 2011). The dataset is available from 1979 to 2016 on a daily basis. Maximum temperature, minimum temperature, rainfall, wind speed, relative humidity and snow water equivalent (SWE) are obtained from ERA-Interim with 0.125° resolution. The variation of maximum and minimum temperatures from 1990 to 1996 for both datasets is shown in Fig. 4a, b. Rainfall data obtained from IMD for this study are of 0.25° resolution. Figure 5a, b shows the spatial variation of rainfall at monsoon, post-monsoon and pre-monsoon period for both IMD (0.25°) and ERA-Interim datasets (0.125°).

Fig. 4
figure 4

Variation of maximum and minimum temperatures from a IMD, b ERA-Interim of Beas basin

Full size image
Fig. 5
figure 5

Spatial variation of a ERA-Interim and b IMD rainfall during monsoon (June–September), post-monsoon (October–January) and pre-monsoon (February–May)

Full size image

Daily precipitation, observed river discharge and sediment yield measurements for study area were obtained from BBMB (Bhakra Beas Management Board) covering the period 1989–2005 at two discharge stations, Pong dam and Pandoh dam. The observed rainfall data for two rain gauge stations, Pong dam (31.9676°N, 75.9471°E) and Pandoh dam (31.6721°N, 77.0662°E), are shown in Fig. 6a, b. Average annual rainfall of Pong dam and Pandoh dam for the study period is 1347.49 mm and 1348.66 mm, respectively.

Fig. 6
figure 6

Observed rainfall data from rain gauge station of Beas river basin of a Pong dam and b Pandoh dam

Full size image

Methodology used

Comparison of the IMD and ERA-Interim

For running a hydrological model like ARCSWAT, meteorological data have a great influence. In recent time, a major challenge is finding high-quality hydrometeorological data. This study investigates whether global reanalysis data products can replace observed hydrometeorological data for use in hydrological modeling for areas where there is a lack of observed data. Moreover, spatial resolution of regional climate models is definitely important in the mountainous areas (Ménégoz et al. 2013). It is a challenge to obtain improved quality precipitation data due to high heterogeneity in topography, sparse network and cold climate. There is an importance to evaluate spatial pattern and temporal variation of existing precipitation datasets. Glacierized basins are more sensitive to temperature because of positive lapse rate as the temperature decreases with elevation. When the temperature increases with elevation, it is negative, and the temperature is zero when it has no change with elevation. Moreover, at high-altitude topography, orographic lifting, a process which forces a mass of air upward can generate snowfall, cloudiness and rainfall. Here the performance of IMD and ERA-Interim datasets is compared with conventional ARCSWAT model. The ERA-Interim data are available at 3-hourly time step, and we calculated the daily mean for all climatic variables obtained from it. In glaciated Beas river basin where the altitude is high, we investigate the relationship between elevation, temperature and rainfall from these two datasets. ArcGIS software is used to carry out a zonal analysis between interpolated mean temperature and rainfall of climate dataset with elevation. The validation of ERA rainfall with observed rainfall data from rain gauge station has also done for three rain gauge stations.

Model setup, calibration and validation

ARCSWAT hydrology model has been utilized for this study to analyze snowmelt runoff and sediment yield of Beas river basin using IMD and ERA-Interim datasets. To get a successful ARCSWAT run, projection and coordinate system should be properly defined. Digital elevation model is used to extract river network. The minimum catchment area of 2000 ha (20 km2) was set to obtain suitable amount of subbasin and number of hydrological response units (HRUs). Thirty-five subbasins and 315 HRUs were finally generated by ARCSWAT. A 10% threshold was set to land use, soil type and slope gradient. According to Sindhu et al. (2013) for ARCSWAT, surface runoff was estimated by Soil Conservation Service Curve Number (SCS-CN) method. Penman–Monteith method was used to estimate evapotranspiration by ARCSWAT hydrology model. For ARCSWAT hydrology model, HRUs are segregated into several subwatersheds (Neitsch et al. 2005). HRUs are the combination of similar spatial units of similar hydrological properties and similar landforms (Neitsch et al. 2005). HRU is the cluster of similar LULC, soils and slopes for individual subbasins and based upon user-defined thresholds. The flow generated from SWAT model is routing of HRUs to watershed outlet. For estimating snowmelt runoff in ARCSWAT, we have to prepare elevation band up to ten from DEM. These elevation bands allow the model to describe the snowmelt process based on basin topography (Hartman et al. 1999). For estimating snowmelt runoff by ARCSWAT, we have to estimate certain variables from elevation band file (Table 2).

Table 2 SWAT input variables to estimate snowmelt runoff
Full size table

Lapse rate including the difference of average and gage elevation is used as a function for calculating maximum temperature, minimum temperature and precipitation for each band. By zonal statistics of DEM and classified DEM, elevation at centre of elevation band is calculated. Fraction of subbasin area within each elevation band is calculated by zonal statistics with shapefile of subbasin. Snow water equivalence obtained from ERA-Interim for each elevation band is calculated. The lapse rate is taken as − 6.5(°C/Km) is the decrease in atmospheric temperature with increase of altitude. According to Liu et al. (2007), Soil Loss Equation (MUSLE) was used for estimating sediment yield and replacing rainfall energy factor used in Universal Soil Loss Equation (USLE) with the runoff. Channel sediment routing computed by Bagnold’s stream power definition involves two concurrent processes, deposition and degradation (Williams 1980). SWAT model has been calibrated and validated for monthly simulated stream flows by comparing with the observed stream flows on the Pong dam and Pandoh dam gauge stations. The model was simulated for 1993–1996 and validated for 1999–2002. SWAT-CUP interface has been used for model sensitivity, uncertainty analysis, calibration and validation. For sensitivity analysis, a comparative change in model output is observed by changing input parameter one by one at one time. Sensitivity analysis leads to efficient calibration due to a significant effect on the simulation output. The simulation results at Pong dam and Pandoh dam include 15 sensitive parameters used for sensitivity analysis. Table 3 shows the parameters selected for the calibration.

Table 3 Parameters for sensitivity analysis in ARCSWAT
Full size table

Model evaluation

Model parameters were calibrated and validated for runoff and sediment yield using the simulation and observation. In addition to relative error, RMSE as an objective function, R2 and Nash–Sutcliffe efficiency (Eqs. 1, 2, 3) are computed.

$${\text{Relative}}\,{\text{error}} = 1/N\mathop \sum \limits_{i = 1}^{N} \left| {Q_{\text{obs}} - Q_{\text{sim}} } \right|/Q_{\text{obs}}$$
(1)
$${\text{RMSE}} = \sqrt {1/N\sum (Q_{\text{obs}} - Q_{\text{sim}} )^{2} }$$
(2)
$${\text{NSE}} = 1 - \left[ {\mathop \sum \limits_{I = 1}^{N} (Q_{\text{obs}} - Q_{\text{sim}} )^{2} /\mathop \sum \limits_{I = 1}^{N} (Q_{\text{obs}} - Q_{\text{obs}}^{\text{mean}} )^{2} } \right]$$
(3)

where RMSE and NSE are the root-mean-square error and Nash–Sutcliffe efficiency, Qobs is the observed stream flow, Qsim is the simulated stream flow, N is the total number of observations and \(Q_{\text{obs}}^{\text{mean}}\) is the average of the observed stream flow.

Results and discussion

A scatter plot between elevation and temperature from IMD and ERA-Interim shows a linear pattern for monsoon (June–September), pre-monsoon (February–May) and post-monsoon period (October–January). There is a decreasing trend of temperature with elevation for IMD with R2 value 0.50 at monsoon, 0.55 at pre-monsoon and 0.50 at post-monsoon period. For ERA-Interim data, we observe a sharp falling trend of temperature with R2 value 0.80 at monsoon, 0.79 at pre-monsoon and 0.81 at post-monsoon period (Fig. 7a–c, e–f). ERA-Interim temperature varies from 7 to 25 °C during pre-monsoon, − 6.65 to 13.25 during post-monsoon and − 2.70 to 19.48 during monsoon season with a elevation of 361 m to 6188 m. IMD temperature varies from 25.5 to 31.6 °C during summer, 13.5 to 15.50 °C during winter and 18.5 to 22.8 °C during monsoon with the same elevation range as ERA-Interim. After analyzing the result, a strong linear relationship has been observed between mean temperature and elevation for all three seasons. The regression coefficient is high, 0.81, during winter for ERA-Interim and for IMD it is high at monsoon, 0.55. The standard deviation of IMD and ERA-Interim mean temperature is 0.87 and 3.5 which indicates that ERA-Interim data have more variation. Over the flat topography, the precipitation decreases with latitude (Li et al. 2018). According to Uhlenbrook et al. (2004), the results of hydrology model were significantly influenced by topographic influence on the rainfall. We select annual rainfall of four months in each season to evaluate precipitation pattern of monsoon (June–September) and winter monsoon (October–January) against elevation. Figure 8a–d shows the variation of rainfall with elevation. According to Fig. 8, the precipitation has an increasing trend with elevation up to 2000 m. Beyond this elevation, the precipitation range becomes larger. A pattern of varying precipitation with elevation is clearer in monsoon than winter for both IMD and ERA-Interim. Precipitation from ERA-Interim varies from 1800 to 3600 mm during monsoon season and 300 to 1100 mm during winter season with the elevation range 361–6188 m. The variations of rainfall from IMD for these two seasons are less than ERA-Interim. The values are 700–2700 mm during monsoon and 250–450 mm, respectively, with elevation. In spite of a huge variance of ERA-Interim rainfall, a significant falling trend was observed for these two rainfall datasets at high elevation than in low elevation.

Fig. 7
figure 7

Variation of mean temperature with elevation for monsoon, pre-monsoon and post-monsoon period for IMD (a–c) and ERA-Interim (d–f)

Full size image
Fig. 8
figure 8

Variation of rainfall with elevation for monsoon and winter period for ERA-Interim (a, b) and IMD (c, d)

Full size image

The correlation between reanalysis and IMD data is below 0.5 during monsoon. There is a good correlation between ERA-Interim precipitation and observed rainfall data than IMD (R2 less than 0.5). Figure 9a, b shows the good match of ERA-Interim and observed rainfall datasets with regression coefficient (R2) of 0.60 and 0.70 at two rain gauge stations such as lower-magnitude station Pong dam and middle-altitude station Pandoh dam. There is a good trend obtained between precipitations from ERA-Interim and observed data for middle-altitude station Pandoh dam. It proves the authenticity of ERA-Interim precipitation data. Figure 10a–d shows the monthly rainfall from 1990 to 2004 for both ERA-Interim and well-known weather datasets at Pong dam and Pandoh dam. It can be observed from Fig. 10 that the variability in the dataset is not the same because maximum and minimum rainfall occurs in almost different years except in a less cases. The average annual rainfall from 1990 to 2004 for ERA-Interim is 2706.76 mm and 2061.196 mm where for IMD theses values are 1253.12 mm and 976.46 mm, respectively, at Pong dam and Pandoh dam.

Fig. 9
figure 9

Comparison of ERA-Interim rainfall data with observed rainfall data at a Pong dam and b Pandoh dam

Full size image
Fig. 10
figure 10

Monthly rainfall data from 1990 to 2004 from ERA-Interim data for a Pong dam and b Pandoh dam and IMD for c Pong dam and d Pandoh dam

Full size image

The calibration and validation of stream flow for Pong dam and Pandoh dam are shown in Figs. 11, 12, 13 and 14 for monthly time steps. According to Moriasi et al. (2007) model appraisal standard at both time steps for most hydrometric stations, it can be observed from Tables 4 and 5 that ERA-Interim dataset produces NSE and R2 values assessed to be satisfactory. However, relative errors are 17.34%, 87.34% for Pong dam and Pandoh dam during calibration, whereas 25.04% and 55.71% during validation for ERA-Interim. For IMD the relative error changed to 29.16% and 150.17% during calibration and 25.62% and 51.45% during validation for two observation stations. The result of ERA-Interim shows a better performance in terms of RMSE and relative error during both calibration and validation periods.

Fig. 11
figure 11

Hydrograph of the observed and calibrated monthly flow for the calibration period of Pong dam for a ERA-Interim and b IMD weather data

Full size image
Fig. 12
figure 12

Hydrograph of the observed and validated monthly flow for the validation period of Pong dam for a ERA-Interim and b IMD weather data

Full size image
Fig. 13
figure 13

Hydrograph of the observed and calibrated monthly flow for the calibration period of Pandoh dam for a ERA-Interim and b IMD weather data

Full size image
Fig. 14
figure 14

Hydrograph of the observed and calibrated monthly flow for the calibration period of Pandoh dam for a ERA-Interim and b IMD weather data

Full size image
Table 4 Relative error (%), RMSE (m3/s), NSE and R2 for simulated river discharge
Full size table
Table 5 Relative error (%), RMSE (m3/s), NSE and R2 for simulated river sediment yield
Full size table

The statistical indicators for sediment yield using ERA-Interim are R2 = 0.65, NSE = 0.42, relative error = 20.34, RMSE = 52.34 during calibration at Pong dam, and for Pandoh dam the values are R2 = 0.67, NSE = 0.52, relative error = 55.23, RMSE = 135.23. During validation R2, NSE, relative error and RMSE values found are 0.72, 0.50, 18.23 and 55.34, respectively, for Pong dam and 0.57, 0.48, 72.34% and 135.12 for Pandoh dam. For IMD the values are R2 = 0.50, 0.51, NSE = 0.38, 0.40, relative error = 30.23%, 73.34% and RMSE = 120.56, 190.56 for Pong dam and Pandoh dam during calibration, whereas during validation the values are R2 = 0.60, 0.47, NSE = 0.45, 0.40, relative error = 25.67%, 93.56% and RMSE = 92.34, 145.32, respectively, for two stations (Figs. 15, 16, 17, 18). The statistical indicator during calibration and validation justifies the model’s better execution using ERA-Interim data for sediment yield.

Fig. 15
figure 15

Observed and simulated monthly sediment yield for model calibration (1993–1996) of Pong dam for a ERA-Interim and b IMD weather data

Full size image
Fig. 16
figure 16

Observed and simulated monthly sediment yield for model validation (1999–2002) of Pong dam for a ERA-Interim and b IMD weather data

Full size image
Fig. 17
figure 17

Observed and simulated monthly sediment yield for model calibration (1996–1999) of Pandoh dam for a ERA-Interim and b IMD weather data

Full size image
Fig. 18
figure 18

Observed and simulated monthly sediment yield for model validation (2002–2005) of Pandoh dam for a ERA-Interim and b IMD weather data

Full size image

This study has been done in the time period of 1993–1996 for calibration and 1999–2002 for validation at Pong dam and 1996–1999 for calibration and 2002–2005 for validation at Pandoh dam as per observed data availability. The Nash–Sutcliffe efficiency and regression coefficient are always better for ERA-Interim than IMD at two locations for both stream flow and sediment yield. Moreover, the mean monthly stream flow and sediment yield during study period vary from 270–950 m3/s and 0–12 t/ha for Pong dam and 20–768 m3/s and 0–12.5 t/ha for Pandoh dam from observational data, whereas by using ERA-Interim and IMD dataset, the stream flow varies from 245 to 975 m3/s and 243 to 750 m3/s at Pong dam and from 0.78 to 375 m3/s and 0.45 to 380 m3/s at Pandoh dam. For sediment yield the values obtained are 0–9.5 t/ha and 0–7.8 t/ha at Pong dam and 0–12 t/ha and 0–7.5 t/ha at Pandoh dam, respectively. As a conclusion, the prediction of hydrological variables using ERA-Interim is quite satisfactory for Beas river basin up to Pong dam.

Conclusion

In this research, an attempt has been done to investigate the trend of ERA-Interim and IMD weather data with elevation and their variability. The ERA-Interim temperature and rainfall data give a satisfactory trend and variation with elevation than IMD for all time period in terms of standard deviation and correlation coefficient. To simulate stream flow of hydrology model accurately, it is essential to give accurate rainfall as input in hydrology model. A good power exponent relationship has been found between ERA-Interim and observed rainfall data for this study area. Moreover, in Beas river basin where snowmelt runoff has a great influence on generating river flow, snowmelt and corresponding runoff response can be modified by changes in air temperature. ERA-Interim which has a significant variation of temperature from − 2.70 to 25 °C has a great influence on snowmelt runoff generation. This current study is a very preliminary attempt that has taken to investigate the performance of ERA-Interim weather data for hydrology modeling by comparing stream flow and sediment yield. There are many other hydrology parameters also like ET, base flow, soil moisture, snow cover, etc. In the future study, these parameters will be tried to be analyzed by hydrology modeling. Moreover, SWAT hydrology model is a river basin scale hydrology model.