Introduction

The increasing population of cities and the development of industries have made the water supply to cities and the design of a distribution network appropriate to them important and complicated. Adequate and safe water supply required by each population is an important aspect of water resources management systems such as urban water distribution networks (Surendra et al. 2021). An urban water supply network must be able to meet the expectations and water demands of consumers in terms of quality [physical, chemical and bacteriological properties of water (Nouiri 2017)] and quantity (flow and water pressure) based on existing standards. Supplying the required water should be possible even in the worst temporal and spatial conditions and emergencies. The design of a water supply system will be satisfactory only if the designers, in addition to sufficient preliminary studies on the hydrological facilities of the site, the amount of available water, the amount of population growth and future industrial development, conduct detailed studies on physical and hydraulic constraints, design criteria and operating costs. Paying attention to these cases leads to the design of a suitable water supply system that meet the needs of that city and region for many years to come. Many efforts have been made to optimize water distribution networks, which have eventually led to the widespread use of modern optimization methods. Haghighi and Asl (2014) used the EPANET simulator model and the NSGA-II optimization algorithm to investigate the uncertainty of water distribution networks, which showed that small uncertainties in input variables can significantly affect network responses as well as reliability performance. They also concluded that NSGA-II plays an important role in systematically solving the problem and improving the computational efficiency of the entire network fuzzy analysis process. Abunada et al. (2014), by locating demand adjustment reservoirs, examined network optimization and reliability. They used a tool called NORAT, which determines demand volume adjustment, optimizes the pipe diameter and reservoir height, evaluates hydraulic reliability of the network and finally calculates the total cost. The achieved results proved the ability of the tool. Hajebi et al. (2014) analyzed the water distribution network using graphical structure partitioning and multi-objective optimization and utilized the water distribution clustering method to find the best arrangement of nodes. Alvisi and Franchini (2014) investigated the optimization of water distribution systems using linear energy balance equations in the framework of ranking-based optimization algorithms and found that this improves computational efficiency and speeds up reaching a near to optimal solution. Creaco and Pezzinga (2015) investigated how incorporating a local search algorithm (LS) such as iterative linear programming (LP) in multi-objective genetic algorithms (MOGA) could reduce search space and then improve the computational performance of MOGAs and proved this assertion through two case studies. Lan et al. (2015) proposed a sustainable optimization model for designing a water supply system by considering the risk of facility failure. The goal was to build facilities that would both save money and stabilize the system. The proposed model was equivalent to a large-scale integer linear program that had been solved by the Banders decomposition algorithm. The computational results describe the efficiency of the proposed algorithm and show that a fundamental improvement in system stability is achieved with a minimal increase in system cost. Di nardo et al. (2016) figured out that partitioning water supply network improves water network management, simplifies water cost calculations, and consequently identifies and reduces water losses. To this end, they used the Swanp software and through two different algorithms based on multi-level recursive and community structure methods, which introduced a multi-objective function and implemented it on a large Mexican network with a certain cost and energy efficiency. Mala-Jetmarava et al. (2017), by collecting two thousand journals from the last three decades that have been working on optimizing water distribution systems, found that mainly optimization has been done on the pump performance to minimize pumping costs and optimize water quality management to achieve standards in nodes. Moosavian (2017) used the multi-linear method for the hydraulic analysis of water distribution networks in several standard and real networks and the results showed that the convergence speed in this method is high and the computational efficiency is almost half the time of other methods. Awe et al. (2020), through a study, modeled and optimized the residential water distribution system of Abuja Post Office, in Nigeria, using the EPANET hydraulic simulation software and the LINGO optimization software, which resulted in a 38% reduction in the total cost of installing, operating and maintaining the water distribution system. Sitzenfrei et al. (2020), using combined network analysis, optimized water distribution networks through determining the optimal decision between costs and performance (e.g., flexibility and leakage) and presented a newly developed design approach. The results indicated that the obtained designs are comparable to the results obtained from evolutionary optimizations, and for large networks (e.g., 150,000 pipes), the execution time is significantly reduced.

Dai (2021) investigated the optimal location of pressure relief valves (PRVs) in water distribution systems by a new optimization model with complementary constraint (MPCCS) for two sample networks and one real network in Vietnam. The results showed the optimal performance of this method in comparison with other optimization methods.

In most researches, the multi-objective optimization of water distribution networks has been studied in a limited way. Also, in all the used methods, the cost objective function is calculated only based on the length and diameter of network pipes, and the cost of violation of the allowable pressure limits in nodes, which is an important factor in increasing the convergence speed of the algorithm, has not been paid attention. Therefore, the purpose of this research is to apply different methods to improve the network performance and modify the problem-solving structure in the form of the NSGA-II and MOPSO algorithms based on the cost and pressure objective functions. Finally, valuable suggestions are provided to extend the proposed method to other networks.

Methods and materials

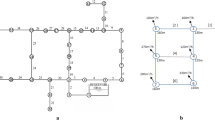
In this research, the hydraulic analysis of water supply networks is performed by the EPANET software and coding of multi-objective NSGA-II and MOPSO algorithms by the MATLAB software. EPANET analyzes the network using gradient method and demand-based analysis method. The network optimization was conducted by linking the MATLAB software to the body of the EPANET software using appropriate computational tools. The efficiency of multi-objective meta-exploration algorithms in solving the problem of the cost optimization and pressure deficit of water supply networks was done through two sample networks that have been studied in many types of research using different algorithms. The use of these two sample networks makes it possible to compare the efficiency of the method used in this research with methods used by other researchers. The first network, introduced by Alperovits and Shamir in 1977, is known as the two-looped network (Alperovits and Shamir, 1977). The network consists of 8 pipes, 7 nodes and a source. The length of all pipes is 1000 m, the Hazen–Williams coefficient is 130 m and the height of water at the source is 210 m. The numbers in parentheses for each node are the height of the node in (m) and the amount of demand in (l/s), respectively, and for each pipe, they are the number of pipes and the diameter of the pipe in (mm), respectively (Fig. 1a). Another sample network was used in 2001 by Lansey et al. (2001). This network has 16 pipes, 11 nodes and a tank. The numbers in parentheses for each node are the height of the node in (m) and the amount of demand in (l / s), respectively, and the network pipe information is given in Table 1 (Fig. 1b).

Fig. 1
figure 1

(a) Two-looped network. (b) Lansey network

Full size image
Table 1 Pipe data for Lansey network
Full size table

Optimization of water supply networks

The problem of multi-objective optimization in this study is defined in such a way that the first goal, i.e., minimizing the cost of network design versus the second goal, i.e., minimizing the total pressure deficit in the entire network.

Objective 1: minimizing network design costs

In order to evaluate the efficiency of the algorithms, the cost function is defined in two ways. In the first method, according to the conventional method in previous research, this function is defined as relation (1) and only considering the cost, diameter and length of pipes, which according to the mathematical relationship between diameter and cost per unit length according to Table 2, is converted to Eq. (2). In the second method, according to Eq. (3), the penalty for exceeding the allowable pressure range is added to the equation.

$$ {\text{Minimize}}\; \, F_{1} = \mathop \sum \limits_{i = 1}^{NL} C_{i} \left( {D_{i} } \right) \times L_{i} $$
(1)
$$ {\text{Minimize }}F_{1} = \mathop \sum \limits_{i = 1}^{NL} \left( {3.5712 \times \exp \left( {0.0081 \times \left( {D_{i} } \right)} \right)} \right) \times L_{i} $$
(2)
$$ {\text{Minimize }}\;F_{1} = ((\mathop \sum \limits_{i = 1}^{NL} \left( {3.5712 \times \exp \left( {0.0081 \times \left( {D_{i} } \right)} \right)} \right) \times L_{i} )/1000) + \, \left( {r \, \times \, \left( {c_{p} + \, c_{m} } \right)} \right) $$
(3)

where \({\text{C}}_{i} \left( {{\text{D}}_{i} } \right)\) is the cost of each unit length of pipe with the diameter Di, Li is the length of the pipe i and NL is the number of pipes in the network (Atiquzzaman et al. 2006).

Table 2 Cost and size of available pipes for network
Full size table

r is the penalty for violation of the allowable pressure range, which is a random number between zero and one hundred. First, different intervals are considered for generating r; then, by implementing algorithms in many iterations and examining the results obtained from different values of r, the best interval (i.e., range 0–100) that leads to the production of the desired optimal solution and higher convergence speed of the problem is chosen. Finally, the selection of r in this selected interval is done randomly each time the model is run. Cp is the cost resulted from the violation of the maximum allowable pressure, and Cm is the cost due to pressures lower than the minimum allowable limit.

$$ C_{p} = \, C_{{p_{ \circ } }} + \left( {\max (\left( {\frac{p}{{p_{{{\text{max}}}} }}} \right) - 1} \right), 0)^{2} $$
(4)
$$ C_{m} = \, C_{{m_{ \circ } }} + \left( {\max \left( {1 - \left( {\frac{p}{{p_{{{\text{min}}}} }}} \right)} \right), 0} \right)^{2} $$
(5)

CP˳ and Cm˳ are considered to be zero, because according to the formula, for a situation where the pressure at the node is considered equal to the minimum or maximum pressure, the cost of exceeding the maximum allowable pressure and the cost resulted by pressures lower than the minimum allowable limit become zero. Pmax and Pmin are considered to be 60 and 30 m, respectively. P is the pressure at the node.

Objective 2: minimizing the total pressure deficit in the network

For this purpose, Eq. (6) is used

$$ {\text{Minimize}}\;F2 = {\text{Minimize}}\mathop \sum \limits_{j = 1}^{NP} \left( {{\text{Max}}\left( {\left( {P_{j}^{{{\text{min}}}} - P_{j} } \right), 0} \right)} \right) $$
(6)

Pjmin is the minimum pressure required at node j, Pj is the computational pressure at node j and NP is the number of nodes in the network.

Constraints of the problem of the optimization of water distribution networks are divided into two categories. The first category, which is in the form of equations, is the continuity equation and the energy conservation equation, which are implemented automatically in the EPANET software and do not need to be defined explicitly in the evaluation function. The second category is unequal and includes diameter and velocity in pipes.

Velocity constraint

The velocity relationship should be as follows in network pipes (Montesinos et al. 1999).

$$ V_{i}^{\min } \le V_{i} \le V_{i}^{\max } \quad i = \, 1, \, 2, \ldots , \, NL $$
(7)

Vi is the velocity in the pipe, \({V}_{i}^{\mathrm{min}}\) is the minimum velocity in the pipe i, and \({V}_{i}^{\mathrm{max}}\) is the minimum velocity in the pipe i. The minimum and maximum velocities in the pipes were considered to be 0.3 and 2 m/s, respectively.

Diameter constraint

The diameter of each pipe must belong to the set of commercial diameters available in the market (Sedki and Ouazar 2012)

$$ D_{i} \in \left\{ D \right\}\quad\forall \;i \in NL $$
(8)

Di is the diameter of the pipe i, and D is the set of available commercial diameters shown in Table 2.

Continuity equation

The sum of the inflow to the node is equal to the sum of the outflow from the node (Sedki and Ouazar 2012).

$$ \mathop \sum \limits_{i = 1}^{NP} Q_{{{\text{in}}}} - \mathop \sum \limits_{i = 1}^{NP} Q_{{{\text{out}}}} = Q_{e} $$
(9)

Qin is the inflow to the node, Qout is the outflow from the node, and Qe is the demand at the node.

Energy conservation equation: The sum of head drops within each loop must be zero (Sedki and Ouazar 2012).

$$ \mathop \sum \limits_{{i \in {\text{loop}}\; l}} \Delta H_{i} = 0\quad\forall l \in NL $$
(10)

\({\Delta \mathrm{H}}_{\mathrm{i}}\) is the head drop within the pipe i.

NSGA-II algorithm

This algorithm was proposed by Deb et al. (2002) and addressed the weaknesses of classical optimization methods such as computational complexity, non-elitism and the need to specify a sharing parameter. It uses elitism to create an optimal Pareto front. The elitist method preserves the good members of the previous generation when applying the operators of the genetic algorithm to produce the new generation, which, in addition to accelerating the convergence to the optimal answer, also makes the search process more efficient. This algorithm, by observing the principle of elitism and with selective function, creates a new population from the combination of the parent and offspring populations by applying mutation and combination operators, and selects the best answers according to their fit and dispersion. In fact, in this algorithm, the responses are first ranked based on dominance and then sorted by the crowding distance (Ahmadianfar et al. 2017). In NSGA-II algorithm, the parameters maximum number of iterations, number of population, percent of crossover and percent of mutation were determined by trial and error. For example, the final value of these parameters in the two-looped network after repeated executions of the model was considered equal to 20, 16, 95 and 5, respectively.

The main structure of the algorithm is shown in Fig. 2 (Deb et al. 2002):

Fig. 2
figure 2

Main structure of the NSGA-II algorithm

Full size image

The implementation steps of the NSGA-II algorithm are as follows:

  1. (1)

    Creating a random initial population of P˳ with the size of N (initial generation of parent)

  2. (2)

    Sort the initial population based on non-dominated answers

  3. (3)

    Rank each non-post answer based on non-dominated balance

  4. (4)

    Apply the selection, combination and mutation operators on P˳ in order to create an offspring population of Q˳ with the size of N.

  5. (5)

    After the production of the first generation, which includes parent and offspring chromosomes, the new generation is produced as follows:

    • Combination of P˳ parent chromosomes and Q˳ offspring and production of the Rt generation with the size of 2 N.

    • Sorting the Rt generation based on the non-dominated classification method and identifying and classifying non-dominated fronts (F1, F2,…)

    • Generating the parent generation with the size of N for the next repetition (\({\mathrm{P}}_{\mathrm{t}+1}\)) using non-dominated fronts. At this stage, according to the number of chromosomes required for the parent generation (N), first the number of chromosomes of the first front for the parent generation is selected, and if this number does not correspond to the total number required by the parent generation, it is taken from fronts 2, 3, etc. to reach the number (N). If we need to select a limited number of chromosomes on one front, the ones with larger crowding distance are selected.

    • Applying the selection, combination and mutation operations on the new parent generation (\({\mathrm{P}}_{\mathrm{t}+1}\)) and the production of the offspring generation (\({\mathrm{Q}}_{\mathrm{t}+1}\)) with the size of N

    • Repeating from step 5 until reaching the stop condition

MOPSO algorithm

The MOPSO algorithm was introduced in 2002 by Coello et al. (2002). This algorithm is a generalized particle swarm optimization (PSO) algorithm that is used to solve multi-objective problems. In the MOPSO algorithm, there is a concept called an archive or storage, in which a set of unsuccessful answers which is an approximation of the Pareto front is archived. The particle swarm optimization algorithm acts based on collective intelligence. In this algorithm, each particle has specific characteristics of position, speed and direction of motion. Motion is important in this algorithm because it exchanges information and creates convergence between particles. Each particle has three sources of information to move, including the behavior that the particle has already shown and is trying to repeat its last activity, the best place it has experienced in the search space and the best place experienced by the whole particles in the search space. In MOPSO algorithm, the parameters of maximum number of iterations, number of population, number of repository and mutation rate were determined by trial and error. The final value of these parameters for two-looped network was (30, 16, 10 and 0.03) and for Lansey network was (250, 32, 10 and 0.03), respectively. The equations describing the particle behavior are as follows:

$$ v_{i} \left( {t + 1} \right) \, = w \times v_{i} (t) + c_{1} r_{1} (x{\text{best}}_{i} (t) - x_{i} (t)) + c_{2} r_{2} (xg{\text{best}}(t) - x_{i} (t)) $$
(11)
$$ x_{i} (t + 1) = x_{i} (t) + v_{i} (t + 1) $$
(12)

\({x}_{i}(t)\) represents the position of the particle i at the moment t, \({v}_{i}(t)\) represents the velocity of the particle i at the moment t, \({x\mathrm{best}}_{i}\) indicates the best previous position of the particle i, and xgbest indicates the position of the best particle in the whole space, so far \({r}_{1}\) and \({r}_{2}\) are random numbers between 0 and 1, c1 and c2 are the acceleration coefficient and w denotes the inertia coefficient.

The steps of implementing the MOPSO algorithm are as follows:

  1. (1)

    Creating an initial population

  2. (2)

    Separating undefeated members of the population and storing them in the storage

  3. (3)

    Tabulating the discovered target space (meaning that according to the minimum and maximum amount of obtained objective functions, divide each of these intervals according to the need into 5–10 equal parts).

  4. (4)

    Selecting a leader from among the storage for each particle and moving it

  5. (5)

    Updating the best personal memory of each particle

  6. (6)

    Adding undefeated members of the current population to the storage

  7. (7)

    Removing defeated members of the storage

  8. (8)

    Due to the lack of memory in the storage, we must reduce their number. If the number of storage members exceeds the specified capacity, we remove the extra members. Cells with larger populations are prioritized for deletion because it is a priority for us to maintain a variety of responses.

  9. (9)

    If the termination conditions are not met, we return to step 3, otherwise the end.

In this algorithm, the selection is done based on regions. The probability of the selection from each cell is calculated from the following equations:

Boltzman Method

$$ p_{i} \propto \exp ( - \beta n_{i} ) $$
(13)
$$ p_{i} = \frac{{e^{{ - \beta n_{i} }} }}{{\mathop \sum \nolimits_{i} e^{{ - \beta n_{i} }} }} $$
(14)

Inverse proportional Method

$$ p_{i} \propto \left( {\frac{1}{{n_{i} }}} \right)^{\beta } $$
(15)
$$ p_{i} = \frac{{(\frac{1}{{n_{i} }})^{\beta } }}{{\mathop \sum \nolimits_{i(} \frac{1}{{n_{i} }})^{\beta } }} $$
(16)

\({p}_{i}\) is the probability of the selection from the cell i, ni represents the number of members in cell i, and β denotes the selection pressure parameter.

To compare the new situation and the best memory of each particle (to update the personal memory in step 5), the following is done:

If the new situation overcomes the best memory, then the new situation replaces the best memory.

If the new situation is defeated by the best memory, nothing will be done.

If none of them defeats each other, one is randomly considered as the best memory.

Optimization–simulation process

EPANET is used for the system simulation and hydraulic analysis of networks. To optimize the network, the EPANET model is linked to each of the NSGA-II and MOPSO algorithms separately using communication tools and mathematical relations in the MATLAB environment. After defining the objective functions and problem constraints, the model is run to reach the set of optimal answers and extract the goal exchange curve until the last iteration of the algorithm. For more information on how to run the model, a summary of the implementation steps of each of these algorithms in linking with the EPANET hydraulic simulator is shown in Fig. 3.

Fig. 3
figure 3

Flowchart steps for run metaheuristic algorithms in connection with the EPANET model

Full size image

Results and discussion

The results of the optimization of sample networks using the NSGA-II and MOPSO algorithms are obtained in two ways. In the first method, the implementation of these algorithms is performed by defining cost functions based on the relationship between the diameter, cost and length of pipes and with the number of repetitions of 10,000 and 20,000. In the second method, the algorithms are implemented by considering the penalty of violation of the allowable pressure limit in the cost function with the number of repetitions that lead to the optimal answer, and the results of both methods are compared with each other and finally with the results of other researchers.

Results of two-looped network optimization

Results of two-looped network optimization in the first method by implementing the NSGA-II and MOPSO algorithms with 10,000 and 20,000 iterations and results of network optimization in the second method by implementing NSGA-II algorithm with 20 iterations, and MOPSO algorithm with 30 iterations by selecting the top 10 answers are shown in the form of Pareto diagrams (Fig. 4). According to Table 3, the selected solutions obtained from the implementation of the NSGA-II algorithm with both methods have a zero pressure deficit that the pressure at the nodes and the velocity in the pipes in the whole network are within the allowable range. The algorithm in the second method has the lowest cost, number of repetitions and execution time, and also has a higher number of near-optimal answers than the first method.

Fig. 4
figure 4

Pareto graphs NSGA-II and MOPSO algorithms in two-looped network

Full size image
Table 3 Top solution NSGA-II and MOPSO algorithms in two-looped network
Full size table

The selected solutions obtained from the implementation of the MOPSO algorithm with both methods have a zero pressure deficit that the pressure at the nodes in the whole network is within the allowable range. The velocity in the pipes in the second method with 30 repetitions is within the allowable range and in the first method with 10,000 and 20,000 repetitions in pipe number 8 and pipe number 4, respectively, and is less than the minimum allowable velocity. The minimum cost amount, number of repetitions and execution time, and maximum number of near-optimal answers are obtained in the second method with 30 repetitions.

This network has been optimized by many researchers with different algorithms. The minimum cost in this study is $ 419,000, and the pressure deficit is zero, which is also found in the present study, with the difference that in this study, in addition to the cost objective function, considering the pressure deficit as an objective function and considering the cost of exceeding the allowable pressure range in the cost function, the convergence rate increased significantly, and with a low number of repetitions, the optimal answer is obtained that demonstrates the superiority of the method used in this research over other research. Table 4 shows the comparison of the results of this study with the results of other researchers.

Table 4 Results from different methods for two-looped network
Full size table

Results of Lansey network optimization

The results of the NSGA-II and MOPSO algorithms in the Lansey network in the first method with 10,000 and 20,000 iterations and the results of the NSGA-II algorithm in the second method with 150 iterations and the MOPSO algorithm with 250 iterations are shown as the top 10 answers in the form of Pareto diagrams (Fig. 5). According to Table 5, the selected solutions obtained from the implementation of the NSGA-II algorithm in both methods have a zero pressure deficit that the pressure at the nodes in the whole network is within the allowable range. In the implementation of the algorithm in the first method, the velocities in pipes 5, 8 and 13 are less than the minimum allowable limit. In the implementation of the algorithm in the second method, the velocity in all network pipes is within the allowable range and the lowest cost, number of iterations and execution time are related to this method.

Fig. 5
figure 5

Pareto graphs NSGA-II and MOPSO algorithms in Lansey network

Full size image
Table 5 Top solution NSGA-II and MOPSO algorithms in Lansey network
Full size table

The selected solutions obtained from the implementation of the MOPSO algorithm in both methods have zero pressure deficit. In the implementation of the algorithm in the first method with 10,000 repetitions, the velocity in pipes 4, 7 and 13 is less than the minimum allowable velocity in the network. In the implementation of the algorithm in the first method with 20,000 repetitions, the velocity in pipes 4, 7, 8, 13 and 15 is less than the minimum allowable velocity. In the implementation of the algorithm in the second method, the velocity in all network pipes is within the allowable range and the lowest cost, number of iterations and execution time are related to this method. The Lansey sample grid, selected by Lansey et al. to reduce the effect of uncertainty on the various conditions of consumption in the grid using the genetic algorithm, with the diameter of the considered pipes costs $ 3,119,022, which after the optimization by the NSGA-II and MOPSO algorithms, a cost of $ 1,137,942, without any network pressure deficits and also high convergence speeds is achieved.

Conclusion

In this study, the optimization of two sample networks of water distribution was performed using the NSGA-II and MOPSO multi-objective algorithms. These algorithms were implemented with two objectives including minimizing cost functions and pressure deficit through two methods (once defining the cost function based on the relationship between diameter, cost and length of pipes, and again, considering the cost of exceeding the allowable pressure limits in the cost function). Their performance was evaluated based on the best response generation and convergence time for both sample networks. The results showed the high ability of algorithms to find optimal solutions. If these algorithms are implemented, by considering the cost of exceeding the minimum and maximum standard pressure threshold in the cost function, the convergence speed will increase significantly, and, in a low number of repetitions, the optimal answer is obtained. This approach will increase the number of near-optimal answers in the last iteration. The modification of the cost function structure in the body of optimization algorithms resulted in optimal results in less time and fewer repetitions in both sample networks than the results of other researchers. In the two-looped network, using the NSGA-II algorithm with 20 repetitions and a run time of 0.66 min, and in the MOPSO algorithm with 30 repetitions and a time of 0.8 min, the lowest cost and lack of pressure (419,000 and zero) are achieved. In the Lansey network, the NSGA-II algorithm after 150 repetitions and execution time of 5.7 min and the MOPSO algorithm with 250 repetitions and the execution time of 9.5 min reached the optimal cost and total lack of zero pressure in the network. Both algorithms offered a lower cost compared to the cost of the diameters proposed by Lansey et al. The results showed that modifying the cost objective function according to Eq. 3 in NSGA-II and MOPSO algorithms limits the search space and significantly reduces the problem-solving time. In this approach, adding a penalty of violation the allowable pressure range to the cost objective function by considering a random parameter in the structure of this function will achieve the optimal solution in the least iteration. This is very important in reducing problem-solving time in larger and more complex water distribution networks and is one of the achievements of this research. By extending this method to real networks with more pipes and more complex structures, the time to achieve the optimal design and modification of the network structure can be significantly improved.