Introduction

As a reservoir engineering method for prediction of development index and recoverable reserve, and dynamic analysis in the water-flooded reservoir, the water drive curves play important role in the oilfield development (Chen and Li 2001; Bondar and Blasingame 2002). Since Maкcимoв (1959) from the former Soviet Union firstly put forward the water drive curve in 1959, a lot of effort has been done worldwide in the research on the water drive curve, e.g. Haзapoв (1972) proposed type D water drive curve in 1972, Tong (1978) introduced the water drive curve proposed by Maкcимoв to China and named it as type A water drive curve in 1978, Caзoнoв (1973) and Tong (1981) conducted research on type B water drive curve and popularized it in the oilfield development, and Cилaчeв (1981) and Haзapoв (1982) proposed type C water drive curve. The researchers in China introduced the curves and conducted the theoretical extension and field application (Tong 1989). Chen (1985, 1993, 1994, 1995, 2000) and Yu and Jin (1995), Yu (1999a, 2000) completed theoretical derivation of formulas for type A, B, C, D, and other water drive curves based on oil–water flow in the porous medium. Zhang (1998) completed derivation of water drive curve that is applied widely in the oilfields. Gao and Xu (2007) also conducted theoretical research based on the ratio of oil and water flow in the porous medium. After decades of development, there are more than 50 types of water drive curves (Yu 2000), among which the conventional water drive curves, i.e. type A, B, C, and D ones, are most used in the oilfield development and chosen as four methods in the standard of China’s oil and gas industry (Yu et al. 1999b). The above four methods were derived theoretically based on the rule of flow in the semi-log linear relation between the ratio of oil and water relative permeability and the water saturation in the oil–water relative permeability curves (Chen 2002; Can and Kabir 2014). Field application showed that the linear relation is applicable in the oilfields at medium–high water cut stage. For the oilfields at ultra-high water cut stage, the rule of fluid flow in the formation has been changed fundamentally, and the ratio of oil and water permeability and the water saturation deviate from the linear relationship in the semi-log curve, showing the downwarping trend with nonlinear relation. Correspondingly, the conventional water drive curves are upwarping at ultra-high water cut stage without linear relationship. Thus, the conventional water drive curves are not applicable in the oilfields at ultra-high water cut stage (Chen and Tao 1997). The conventional water drive curves would result in higher recoverable reserve and recovery, creating the big error. Currently, there are few reports about the new formula of the relation between the ratio of oil and water permeability and the water saturation in oilfields at ultra-high water cut stage. Only Liu et al. (2011), Wang et al. (2013), Song et al. (2013), and Cui et al. (2015) in China proposed the exponential and binomial equations for the relation between the ratio of oil and water permeability and the water saturation, completed derivation of exponential, binomial, and inverse-proportion water drive curves, which have some limitations in prediction accuracy. Thus, it needs more effort to work out the water drive curve for the oilfields at ultra-high water cut stage. This paper aims at establishing the new formula of the relation between the ratio of oil and water permeability and the water saturation, based on which the new water drive curve is obtained. The numerical and field application confirmed the applicability of the new water drive curve in prediction of development index, recoverable reserve, and recovery, which is of significance to improvement of evaluation methods of oilfields at ultra-high water cut stage.

New formula of ln(K ro/K rw)−S w at ultra-high water cut stage

Characteristics of ln(K ro/K rw)−S w curve

The logarithm of ratio of oil and water relative permeability ln(K ro/K rw) decreases as the water saturation S w increases. The curve includes three stages: I is the low water cut stage, II is the medium–high water cut stage, and III is the ultra-high water cut stage. At the medium–high water cut stage, ln(K ro/K rw) and S w show the linear relation, based on which the conventional water drive curves are derived theoretically (Figs. 1, 2). The formula for II linear relation is expressed as (Craig 1971):

$$\ln \frac{{K_{\text{ro}} }}{{K_{\text{rw}} }} = \alpha - \beta S_{\text{w}}$$
(1)

namely:

$$\frac{{K_{\text{ro}} }}{{K_{\text{rw}} }} = ne^{{ - mS_{\text{w}} }}$$
(2)

where K ro is the oil relative permeability, decimal; K rw is the water relative permeability, decimal; S w is the water saturation at the outlet, decimal; α and β are the slope and the intercept, respectively; m and n are K ro/K rw and the constant of S w at the outlet, respectively.

Fig. 1
figure 1

Curves of oil and water relative permeability

Full size image
Fig. 2
figure 2

Water drive curves

Full size image

For the oilfields at ultra-high water cut stage, the curves of ln(K ro/K rw) and S w show the downwarping trend and transform from II linear relationship to III nonlinear relationship, and the water drive curves show the upwarping trend. The main reason is that as the water saturation increases, the oil of continuous phase in the formation transforms to partially continuous phase and non-continuous phase, causing the stronger Jamin effect, substantial reduction in oil permeability, and increment of water permeability, and thus resulting in the downwarping curve of ln(K ro/K rw) and S w which has the intrinsic rule consistent with conventional water drive curves showing upwarping trend at ultra-high water cut stage. Application of the conventional water drive curves in analysis of development dynamics of the oilfields at ultra-high water cut stage would result in big error of water cut and higher predicted recoverable reserves. Thus, the formula of ln(K ro/K rw) and S w characterizing oil and water flow in the oilfields at ultra-high water cut stage is needed to derive the new water drive curve, which is of significance to improvement of the evaluation methods of water-flooded reservoir at ultra-high water cut stage.

New formula of K ro/K rw−S w

Formula (1) describes the typical relation between ln(K ro/K rw) and S w at the medium–high water cut stage, but it could not be used in the oilfields at ultra-high water cut where ln(K ro/K rw) and S w deviate from the linear relation. The statistics of relative permeability data from 386 core samples in the Daqing Oilfield showed the obvious nonlinearity, e.g. the curve of ln(K ro/K rw) and S w showed the downwarping trend with water cut between 91 and 93% and inflection points with water cut between 93 and 94%. Normalization of relative permeability data from 15 samples of Nan_1 Block of Sanan Zone in the Daqing Oilfield, 21 samples of Xing_10 of Xingnan Zone, and 17 samples of Xing_5 Block of Xingbei Zone was conducted with average relative permeability method (Table 1), and the curve of K ro/K rw and S w was plotted (Fig. 3) in the semi-log coordinate by reference to data of oil–water relative permeability of Zhuang_19 Well Block in the Xifeng Oilfield (Song et al. 2013).

Table 1 Data of relative permeability from cores of different zones
Full size table
Fig. 3
figure 3

Curve of K ro/K rw and S w of cores from different zones

Full size image

It is shown in Fig. 3 that K ro/K rw and S w in the semi-log coordinate deviate from the linear relation in different degree at ultra-high water cut stage. With statistics of relative permeability data of cores, the formula of ln(K ro/K rw) and S w at ultra-high water cut stage was derived:

$$\ln \frac{{K_{\text{ro}} }}{{K_{\text{rw}} }} = a + b\left( {S_{\text{w}} - S_{\text{wc}} } \right) - c\left( {S_{\text{w}} - S_{\text{wc}} } \right)^{n}$$
(3)

where a, b, c, and n are constant, which are calculated with the methods in this paper; S w is the water saturation at the outlet, decimal; S wc is the irreducible water saturation, decimal.

The migration segment with ultra-high water cut in Fig. 3 was fitted using formula (3), which is shown in Fig. 4, and the new formula of K ro/K rw and S w was obtained through regression, which is shown in Table 2. The above figure and table showed the high precision of formula (3) fitting the relation between ln(K ro/K rw) and S w at ultra-high water cut stage and confirmed that formula 3 could characterize the relation between K ro/K rw and S w not only at ultra-high water cut stage but also at the high water cut stage, with more fitted data points and higher

correlation coefficient than the method in reference where the formula is ln(K ro/K rw) = −548.1S 2w +639.25S w−187.56 with correlation coefficient of 0.9950 (Song et al. 2013). Thus, formula (3) is applicable in theoretical derivation of new water drive curve and its field application. Moreover, formula 3, which characterizes the relation between K ro/K rw and S w at ultra-high water cut stage, has higher precision than formula 1 for medium–high water cut stage and the binomial equation of K ro/K rw and S w for the ultra-high water cut from reference Song et al. (2013).

Fig. 4
figure 4

Fitting of migration segment of K ro/K rw−S w curve

Full size image
Table 2 Result of fitting of migration segment of K ro/K rw−S w curve
Full size table

New water drive curve

Theoretical derivation of formula for new water drive curve

Based on the above formula of ln(K ro/K rw) and S w for the ultra-high water cut, derivation of corresponding water drive curve was done with the reservoir engineering method (Buckley and Leverett 1942).

According to the relation between the ratio of oil and water relative permeability and the water saturation in formula (3), the following formula was obtained:

$$\frac{{K_{\text{rw}} }}{{K_{\text{ro}} }} = \frac{{e^{{\left[ { - b\left( {S_{\text{w}} - S_{\text{wc}} } \right) + c\left( {S_{\text{w}} - S_{\text{wc}} } \right)^{n} } \right]}} }}{{e^{a} }}$$
(4)

In case of neglecting the gravitational effects and capillary force, the relation between the ratio of oil and water relative permeability and the oil–water production under the steady flow of water flooding is expressed as:

$$\frac{{K_{\text{rw}} }}{{K_{\text{ro}} }} = \frac{{Q_{\text{w}} \mu_{\text{w}} B_{\text{w}} \gamma_{\text{o}} }}{{Q_{\text{o}} \mu_{\text{o}} B_{\text{o}} \gamma_{\text{w}} }}$$
(5)
$$\frac{{Q_{\text{w}} }}{{Q_{\text{o}} }} = \frac{{f_{\text{w}} }}{{1 - f_{\text{w}} }}$$
(6)

where Q o is the oil production on the ground, t/d; Q o is the water production on the ground, t/d; μ o and μ w are the oil and water viscosity in the formation, respectively, mPa·s; B o and B w are the volume factors of oil and water in the formation, dimensionless; γ o and γ w are the relative densities of the degassed oil and the water on the ground, dimensionless; f w is the water cut, dimensionless.

With formulas (4), (5), and (6), the formula for water–oil ratio WOR is expressed as:

$${\text{WOR}} = \frac{{f_{\text{w}} }}{{1 - f_{\text{w}} }} = \frac{{Q_{\text{w}} }}{{Q_{\text{o}} }} = \frac{{\mu_{\text{o}} B_{\text{o}} \gamma_{\text{w}} }}{{\mu_{\text{w}} B_{\text{w}} \gamma_{\text{o}} }}\frac{{e^{{\left[ { - b\left( {S_{\text{w}} - S_{\text{wc}} } \right) + c\left( {S_{\text{w}} - S_{\text{wc}} } \right)^{n} } \right]}} }}{{e^{a} }} = \frac{{\mu_{\text{o}} B_{\text{o}} \gamma_{\text{w}} }}{{e^{a} \mu_{\text{w}} B_{\text{w}} \gamma_{\text{o}} }}e^{{\left[ { - b\left( {S_{\text{w}} - S_{\text{wc}} } \right) + c\left( {S_{\text{w}} - S_{\text{wc}} } \right)^{n} } \right]}}$$
(7)

Logarithm transformation on both sides of formula (7), then:

$$\lg {\text{WOR}} = \lg \frac{{\mu_{\text{o}} B_{\text{o}} \gamma_{\text{w}} }}{{e^{a} \mu_{\text{w}} B_{\text{w}} \gamma_{\text{o}} }} + 0.4343\left[ { - b\left( {S_{\text{w}} - S_{\text{wc}} } \right) + c\left( {S_{\text{w}} - S_{\text{wc}} } \right)^{n} } \right]$$
(8)

When the oilfields enter into the high water cut stage, especially the ultra-high water cut stage, the average water saturation in the oil layer is written as (Bondar and Blasingame 2002; Chen and Tao 1997):

$$\overline{{S_{\text{w}} }} = S_{\text{w}}$$
(9)

The accumulative oil production is expressed as:

$$N_{\text{p}} = 100Ah\phi \frac{{\gamma_{\text{o}} }}{{B_{\text{oi}} }}\left( {\overline{S}_{\text{w}} - S_{\text{wc}} } \right)$$
(10)

Thus, based on the matter balance equation and formula (10) for the accumulative oil production, the relation between the average water saturation and the recovery per cent is expressed as:

$$\overline{S}_{\text{w}} = \frac{{1 - S_{\text{wc}} }}{N}N_{\text{p}} + S_{\text{wc}} = \left( {1 - S_{\text{wc}} } \right)R + S_{\text{wc}}$$
(11)

where A is the area of oil reservoir, km2; h is the effective thickness of oil layer, m; ϕ is the porosity of reservoir; \(\overline{S}_{\text{w}}\) and S wc are the average water saturation and the irreducible water saturation, respectively; B oi is the initial volume factor of oil; N is the geological reserve, 106t; N p is the accumulative oil production, 106t; R is the recovery per cent of oilfield, dimensionless.

Combining formulas (9) and (11) yields:

$$S_{\text{w}} - S_{\text{wc}} = \frac{{1 - S_{\text{wc}} }}{N}N_{\text{p}}$$
(12)

Substituting formula (12) into formula (8) yields:

$$\begin{aligned} \lg {\text{WOR}} = \lg \frac{{\mu_{\text{o}} B_{\text{o}} \gamma_{\text{w}} }}{{e^{a} \mu_{\text{w}} B_{\text{w}} \gamma_{\text{o}} }} + 0.4343\left\{ { - b\frac{{1 - S_{\text{wc}} }}{N}N_{\text{p}} + c\left[ {\frac{{\left( {1 - S_{\text{wc}} } \right)}}{N}N_{\text{p}} } \right]^{n} } \right\} \\ = \lg \frac{{\mu_{\text{o}} B_{\text{o}} \gamma_{\text{w}} }}{{e^{a} \mu_{\text{w}} B_{\text{w}} \gamma_{\text{o}} }} - 0.4343b\frac{{1 - S_{\text{wc}} }}{N}N_{\text{p}} + 0.4343c\left( {\frac{{1 - S_{\text{wc}} }}{N}} \right)^{n} N_{\text{p}}^{n} \\ \end{aligned}$$
(13)

Define

$$A = \lg \frac{{\mu_{\text{o}} B_{\text{o}} \gamma_{\text{w}} }}{{e^{a} \mu_{\text{w}} B_{\text{w}} \gamma_{\text{o}} }},\quad B = - 0.4343b\frac{{1 - S_{\text{wc}} }}{N},\quad C = 0.4343c\left( {\frac{{1 - S_{\text{wc}} }}{N}} \right)^{n}$$
(14)

Substituting formula (14) into formula (13), the formula for water drive curve characterizing the oil–water seepage characteristics in the oilfields at ultra-high cut stage is expressed as:

$$\lg {\text{WOR}} = A + BN_{\text{p}} + CN_{\text{p}}^{n}$$
(15)

Assuming R = N p/N, then the formula between the water–oil ratio (WOR) and the recovery per cent (R) is expressed as:

$$\lg {\text{WOR}} = A_{1} + B_{1} R + C_{1} R^{n}$$
(16)

where A 1 = A, B 1 = BN, C 1 = CN n.

When n = 1, formula (15) is transformed into:

$$\lg {\text{WOR}} = A + \left( {B + C} \right)N_{\text{p}}$$
(17)

Defining B ′ = B + C, then

$$\lg {\text{WOR}} = A + B^{\prime} N_{\text{p}}$$
(18)

Formula (18) characterizes the conventional water drive curve. The new water drive curve is transformed to the conventional one when n = 1. The water drive curve derived in this paper integrates the water drive curve at the medium–high water cut stage and that at ultra-high water cut stage, and it is more universal than the conventional one.

When the oilfields reach the abandonment condition, i.e. f w = 98%, WORmax = 49, the formula for calculating the recoverable reserve of water-flooded oilfields is obtained with formula (15), then:

$$N_{\text{R}}^{n} = \frac{{1.69 - A - BN_{\text{R}} }}{C}$$
(19)

The recoverable reserve of water-flooded oilfield \(N_{\text{R}}\) in formula (19) is obtained with curve intersection method, and then the recovery of water-flooded oilfield is obtained with \(E_{\text{R}} = N_{\text{R}} /N\).

Solution to parameters

The new water drive curve is more complex and has more parameters than the conventional one, and it is difficult to calculate the parameters directly. Thus, the parameters of new water drive curves were derived with the new method.

Taking the derivative of the accumulative oil production N p on both sides of formula (15) yields:

$$\frac{{{\text{d}}\left( {\lg {\text{WOR}}} \right)}}{{{\text{d}}N_{\text{p}} }} = B + CnN_{\text{p}}^{n - 1}$$
(20)

namely

$$\frac{{{\text{d}}\left( {\lg {\text{WOR}}} \right)}}{{{\text{d}}N_{\text{p}} }} - B = CnN_{\text{p}}^{n - 1}$$
(21)

Logarithm transformation on both sides yields:

$$\lg \left[ {\frac{{{\text{d}}\left( {\lg {\text{WOR}}} \right)}}{{{\text{d}}N_{\text{p}} }} - B} \right] = \lg Cn + \left( {n - 1} \right)\lg N_{\text{p}}$$
(22)

The curve of \(\lg \left[ {\frac{{{\text{d}}\left( {\lg {\text{WOR}}} \right)}}{{{\text{d}}N_{\text{p}} }} - B} \right]\sim\lg N_{\text{p}}\), which meets the linear relation, was plotted. The value of B was defined with the trial and error method, which is shown in Fig. 5. n, C, and A were obtained according to straight slope, straight intercept, and dynamic data, respectively. The time t i when the better linear relation exists was chose, then A i = (lgWOR) ti−BN pti−C(N pti)n. After calculating the values of A i, the average value \(A = \sum\nolimits_{i = 0}^{n} {A_{\text{i}} } /n\) with higher precision was calculated. Thus, the parameters in the formula for the new water drive curve were obtained.

Fig. 5
figure 5

Parameters determining in new water drive curve by linear trial and error method

Full size image

Validation and analysis

Validation of numerical simulation

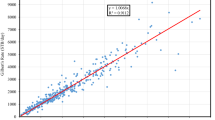
Based on the oil reservoir conditions of Pu_1 Formation of Xing_10 Block of Xingnan Zone in the Daqing Oilfield, the model of five-spot pattern with injector-producer well spacing of 254 m, grid number of 15 × 15 × 3 in IJK direction, and areal mesh size of 24 m was established. The dynamics of oilfields with different ratios of oil and water viscosity were predicted with reservoir numerical simulation, and fitting and comparison of the conventional water drive curve and the new water drive curve were conducted with production data. The fitting result is shown in Fig. 6.

Fig. 6
figure 6

Comparison of fitting with different water drive curve. a Conventional water drive curves, b new water drive curves

Full size image

It is shown in Fig. 6 and Table 3 that the conventional water drive curves are applicable only in the linear segment, not in the upwarping segment. The new water drive curve, however, could fit both linear segment and curving segment with correlation coefficient over 0.9976. Moreover, in terms of the recoverable reserve, all the values predicted by the conventional water drive curves are much larger than those predicted by numerical simulation, but the value predicted by the new water drive curve is closed to that predicted by numerical simulation with little error. It means that the new water drive curve could fit the data at the high water cut and ultra-high water cut stage with accurate recoverable reserve and has broad adaptability in the oilfields.

Table 3 Formula for water drive curves and calculation of recoverable reserve
Full size table

Examples

The accuracy and adaptability of the new water drive curve in the oilfields at ultra-high water cut stage were verified with actual data from reference Song et al. (2013), Cui et al. (2015).

Calculation according to Craig FF Jr

Given reference Craig (1971), Song et al. (2013), the original oil in place is 4.44 × 104t, the initial water saturation is 0.1, the well pattern is the five-spot pattern, and the ratio of oil and water viscosity is 2. The recovery per cent, accumulative oil production, accumulative water production, and other production data corresponding to different water saturation at the outlet are shown in Table 4.

Table 4 Dynamic data of oilfield
Full size table

Based on the data in Table 4, the curve of lgWOR and accumulative oil production N p was plotted with the new water drive curve to compare the new and conventional water drive curves, which are shown in Fig. 7. The front half segment of lgWOR−N p curve shows the linear relation of the conventional water drive curve, and the latter half segment shows the obvious upwarping trend, which is not the linear relation, and could not be fitted with the conventional water drive curve. Therefore, both front and latter half segments of curve were fitted using new and conventional water drive curves, with which the water-flooded recoverable reserve is predicted for comparison with the results in reference Song et al. (2013) (Table 5).

Fig. 7
figure 7

Curve of water–oil ratio and accumulative oil production

Full size image
Table 5 Prediction of water-flooded recoverable reserve with different water drive curves
Full size table

The fitting results of Fig. 7 show that the latter half segment of lgWOR−N p curve is well fitted with the new water drive curve with correlation coefficient of 0.9987. The actual water-flooded recoverable reserve resulted from Table 4 is 2.792 × 104t, which is defined as the accumulative oil production with water cut of 0.98, and that calculated by the new water drive curve is 2.7964 × 104t with relative error of merely 0.1576%, which has very high prediction precision. However, the water-flooded recoverable reserve predicted in reference Song et al. (2013) by the water drive curve at ultra-high water cut and the conventional curves has big error, with prediction precision far lower than the methods in this paper. It is believed in reference Song et al. (2013) that the water drive curve of oilfields with high water cut shows the parabola shape. However, the curve of lgWOR−N p is not completely consistent with parabola shape, and the recoverable reserve predicted by binomial water drive curve in reference Song et al. (2013) has big error and is not useful. The comparison of predicted water in Fig. 8 shows that the new water drive curve predicts the water cut more accurately than the conventional one. In conclusion, the new water drive curve at ultra-high water cut predicts the water-flooded recoverable reserve and water cut more accurately than other water drive curves and has better adaptability.

Fig. 8
figure 8

Curves of water cut predicted by the new water drive curve and the conventional one

Full size image

Example in the Shengli Oilfield

The accuracy and adaptability of the new water drive curve were verified with actual data from reference Cui et al. (2015) (Table 6), which was fitted with the new and conventional water drive curves (Fig. 9). The water-flooded recoverable reserve, which is defined as the accumulative oil production with comprehensive water cut of 0.98, and the water cut were predicted and compared with actual data of oilfields for comparison of the water drive curves in this paper and that in reference Cui et al. (2015).

Table 6 Actual development data in Shengli oilfield
Full size table
Fig. 9
figure 9

Comparison of fitting with different water drive curves

Full size image

Based on the data in Table 6, lgWOR−N p curve was plotted, and it showed the upwarping trend at ultra-high water cut stage. The parameters of new water drive curve were calculated with formula (22), and the formula of conventional water drive curve was fitted, which is shown in Table 7. It is shown in Fig. 9 that fitting the segment at ultra-high water cut stage in lgWOR−N p curve could not be done with the conventional water drive curve, but could be done with the new one proposed in this paper.

Table 7 Water-flooded recoverable reserve predicted with different water drive curves
Full size table

With comprehensive water cut of 98%, the water-flooded recoverable reserve predicted by the new water drive curve, the conventional one, and the water drive curve at ultra-high water cut in reference Cui et al. (2015) are 83.9841 × 104t, 126.0783 × 104t, and 84.80 × 104t, respectively, with error of 0.0166, 50.1465, and 0.988% based on the actual water-flooded recoverable reserve of 83.9702 × 104t. Among the water drive curves, the method proposed in reference Cui et al. (2015) has a large disadvantage because S or and S wc depend on other static data and have uncertain value, and it is difficult to work out the formula. Comparison of water cut predicted with the method of water drive curve in Fig. 10 showed that the water cut predicted in this paper is very closed to the actual data. By contrast, the water cut predicted by conventional water drive curve is far less than the actual data, which results in much larger water-flooded recoverable reserve. Obviously, the new water drive curve at ultra-high water cut predicts the water-flooded recoverable reserve and water cut more accurately than other water drive curves and has better adaptability.

Fig. 10
figure 10

Comparison of water cut predicted by different water drive curves

Full size image

Conclusions

  1. (1)

    For the oilfields at ultra-high water cut stage, the rule of fluid flow in the formation has been changed fundamentally, and the ratio of oil and water permeability and the water saturation deviate from the linear relationship and show the downwarping trend in the semi-log curve. Thus, the new formula of the ratio of oil and water permeability and the water saturation more applicable in the oilfields was proposed to characterize the curve of K ro/K rw and S w at ultra-high water cut stage and high water cut stage.

  2. (2)

    Based on the new formula of K ro/K rw and S w at ultra-high water cut stage, the new water drive curve was derived with the reservoir engineering method. The new water drive curve is transformed to the conventional one when n = 1. Comparison of prediction with new water drive curve, conventional one, and methods in references 27 and 28 was done with numerical simulation and field application in two oilfields, which showed that the new water drive curve could fit the development data both at the high water cut and at the ultra-high water cut stage and characterize the upwarping trend at ultra-high water cut stage. The new water drive curve at ultra-high water cut predicts the water-flooded recoverable reserve and water cut more accurately than other water drive curves and has better adaptability.