An investigation on the effects of silica and copper oxide nanoparticles on rheological and fluid loss property of drilling fluids

Abstract

The increase in hydrocarbon production from problematic production zones having high fluid loss and formation damage has led to the emergence of non-damaging drilling fluids (NDDF). Recently, nanotechnology has found a wide array of applications in the oil and gas industry. Most applications of nanotechnology and enhancement in properties of drilling fluids are restricted to bentonite, xanthan gum and a few oil-based mud. In this study, the effects of silica and copper oxide nanoparticles on polyamine-based NDDF and conventional bentonite-based drilling fluids (BDF) were investigated. Silica nanoparticles were prepared using sol–gel method, and copper oxide nanoparticles were synthesized using co-precipitation method. Nano-based drilling fluids were prepared by dispersing nanoparticles in concentrations of 0.5%, 0.8% and 1% by weight. Furthermore, testing of these nano-based drilling fluids was conducted by measuring specific gravity, pH, rheological properties and filtrate loss at surface temperature (room temperature) and then aging it at bottom-hole temperature (80 °C). The addition of silica and copper oxide nanoparticles to both the drilling fluids did not show much effect on pH and specific gravity. Addition of 0.5% concentration of silica nanoparticles in NDDF showed least degradation in rheological properties compared to other fluids. It showed reduction in filtrate loss by 31%. Moreover, silica nanoparticles in conjunction with BDF acted as a mud thinner showing a decrease in viscosity and yield point. On the contrary, when used with NDDFs, silica nanoparticles acted as a mud thickener. Copper oxide nanoparticles behaved as a thinner in both the drilling fluids with a highest reduction in plastic viscosity of 24% for 0.8% of copper oxide nanoparticle in BDF. Thinning properties were enhanced as the doping concentrations of copper oxide nanoparticles increased; however, the fluid loss controlling ability decreased except for 0.5% concentration by 31% and 24% when used with both the drilling fluids. Additionally, optimal Herschel–Bulkley parameters have been determined by using genetic algorithm to minimize the function of sum of squared errors between observed values and model equation.

Introduction

Drilling fluid is an indispensable component of oil and gas industry. Primarily, these fluids are used to control or subdue the formation pore pressure and carry rock cuttings from the bottom of the hole to the surface, where they are recycled. Apart from these, several other functions are performed by the drilling fluid that are attained by designing it with suitable rheological properties of yield point, plastic viscosity, apparent viscosity and gel strength. The specific gravity of the drilling fluid should be such that it provides a hydrostatic head greater than the formation pressure to prevent any kind of influx or entry of formation fluids inside the well. The weighing agents require higher viscosity and yield point so that the hole cleaning process is not effected by sagging of these agents (Ogbeide and Igbinere 2016). A mud thickener is often the practiced solution in the industry, whereas, to reduce the magnitude of yield point and viscosity, mud thinners often come into play (Mullen et al. 2005). Filtrate loss through the mud cake around the borehole wall causes damage to the formation and also in shale sections leads to shale swelling causing stuck-ups (Srivatsa and Ziaja 2012). Moreover, fluid loss in the production zone damages the reservoir by blocking the near well bore pore throats, altering the wettability and decreasing the relative permeability to oil in the sand phase region. This results in lower production rates, and hence, a stimulation job becomes inevitable incurring more expenses. This problem in shale and in production zone has led to the emergence of non-damaging drilling fluids (NDDF), which is fundamentally a solid-free drilling fluid (Talukdar and Gogoi 2015). Nanotechnology is one of the key inventions of the twenty-first century. For the last few decades, it is helping to create new materials, opening up possibilities in manufacturing and providing opportunities for a wide array of applications which would immensely impact our existing technology, environment and society (Wong and De Leon 2010). The efficient impact of nanoparticles (NPs) is often due to its increase in surface area to volume ratio, which enhances interaction sites. Additionally, NPs can act as receptors for polymers which allow functionalization and coating over it (Mao et al. 2014; Sneh and George 1995). The hydrophobicity or hydrophilicity of some NPs enables them to find wide application in many industries (Tuteja et al. 2008). These attributes of NPs had drawn the attention of many researchers who have investigated its application in upstream oil and gas industry (Barry et al. 2015; Ponmani et al. 2013). It has been observed that interfacial parameters can be altered in a reservoir rock by the use of NPs and nanostructured surfactants when used with flooding fluids. An investigation was carried out to study the changes in interfacial tension, wettability and capillary profiles during heavy oil recovery by Mohebbifar et al. (2014). Cheraghian et al. (2013) investigated the use of titanium oxide and fumed silica NPs for enhanced oil recovery (EOR) processes and enhanced performance of drilling fluids with successful results. Designing nanostructured coating in drill bits and drilling fluids in high-pressure high-temperature (HPHT) environment also has been explored with positive results (Hiller 1963). NPs can be used with emulsions during oil well cementing for strengthening and increasing cement durability (Maserati et al. 2010). In the production phase, NPs can tackle problems of removing asphaltene, scale, corrosion and gas hydrates especially in pipelines, tubing and separators (Shah et al. 2010).

In another research, the effects of adding iron and calcium NPs to non-aqueous drilling fluids were investigated where the optimum concentration of both iron and calcium NPs enhanced the fracturing pressure by 39% and 63%, respectively, and proved to be a good fluid loss additive and wellbore strengthening material for applications in permeable formations (Contreras et al. 2016). This was further confirmed by the investigations carried out by Yu et al. 2017, where the characteristics of NPs and their potential to become a drilling fluid additive were highlighted. They further emphasized the enhancement in the rheological properties of drilling fluids upon the introduction of suitable NPs, which assists in optimizing the overall efficiency of the drilling process. These NP-based drilling fluids serve to eliminate a number of downhole problems including pipe stuck conditions, loss circulation, formation damage, high filtrate loss, poor quality of mud cakes as well as high torque and drag. A variety of tests and experiment were performed on these NP-based drilling fluids, all of which have ascertained that these novel fluids are far more superior to the conventional drilling fluids in almost all aspects, and are capable enough to replace them in future. Additionally, a comprehensive study using analytic hierarchy process analysis was conducted on the application of nanotechnology on all the aspects of the upstream oil industry and it was observed that nanotechnology can be used to enhance the performance of drilling fluids under HPHT conditions (Motamedi et al. 2018).

Most of the research has been conducted to study the interaction of NPs with bentonite drilling fluid (BDF). A very few have been conducted with oil-based fluid with little or not much positive results. Most of the production zones are treated with NDDF, which leaves a very little scope for BDF to interact with the reservoir. Hence, the study of effect of NPs in NDDF with detailed study of its effect on rheological behavior and the property of fluid loss control is more essential.

In the current work, the effects of NPs in conventional BDF and NDDF were investigated. The performance of the NP-based BDF and NDDF was characterized by carrying out rheology testing with rotational type Fann viscometer, and the magnitude of filtrate loss was measured by an API filter press apparatus. The performances of these NPs-based BDF and NDDF were compared with the performance of base fluids (without NPs). All these performances were evaluated by characterizing the mud in ambient as well as after exposing it to bottom-hole temperatures (80 °C) for 16 h.

Materials and methods

Synthesis of silica (SiO₂) NPs

The silica NP used in the current study was synthesized by sol–gel process. This process primarily consists of two stages: hydrolysis of the precursor TEOS (tetraethyl orthosilicate) and condensation/polymerization to form entire silica structure (Rahman and Padavettan 2012). During the network formation process, a large amount of solvent are also impregnated in the network, and thus, a gel is formed. In the current process, 1 g of TEOS, 3 g of ammonia and 4 g of ethanol were added in water and magnetically stirred at ambient conditions for 1.5 h. Further, 2 g of TEOS and 8 g of ethanol were added and stirred for the next 2 h. A gel-like solution was eventually formed which was kept in the oven for 24 h at 65 °C. Dried gel in amorphous form was then calcined for 4 h at 400 °C to obtain a crystalline structure and ground using an agate motor.

The surface roughness obtained with the sol–gel method can be easily modified by changing the synthesis procedure and composition of the reaction mixture. Basu et al. 2010 fabricated binary micro-/nanostructured sol–gel coatings by spraying precursor mixtures containing hydrophobically modified silica (HMS) NPs dispersed in sol–gel matrices prepared with acid-catalyzed TEOS. The hydrophobicity of the coatings was increased with increase in the concentration of HMS NPs. Superhydrophobic coatings with water contact angle of 166° and roll off angle 2° were obtained by optimizing the sol–gel processing parameters and the concentration of silica NPs in the coating. After dip coating the silica sol onto cotton surfaces, the surfaces were modified with hexadecyltrimethoxysilane (HDTMS) to obtain a thin layer through self-assembly. The treated cotton fabrics exhibited superhydrophobicity.

Synthesis of copper oxide (CuO) NPs

Precipitation method was adopted for the synthesis of copper oxide (CuO) NPs by using copper chloride (CuCl₂) and copper nitrate (Cu(NO₃)₂.3H2O). 0.1 M solution for each precursor was prepared by dissolving it in deionized water. Sodium hydroxide (NaOH) solution (0.1 M) was added dropwise under vigorous stirring until a pH of 13–14 was attained. A black precipitate was obtained which was washed repeatedly by deionized water and successively with ethanol to neutralize the pH to 7. The precipitate was then dried at 80 °C for 16 h. Finally, the dried precipitate was calcined at 500 °C for 5 h and ground (Malviya et al. 2015).

For both the synthesized particles, XRD was carried out for validation and particle sizes were calculated by using Debye–Scherrer equation, given by:

$$D = \frac{0.9\lambda }{\beta \cos \theta }$$

where λ is the wavelength of X ray and β is the full width at half minimum (radians) of peak at 2θ.

Particle size range of 22–48 nm was obtained for silica (SiO₂) NPs and 27–53 nm for CuO NPs (Saleh and Gupta 2016; Saleh 2017) (Figs. 1, 2).

Fig. 1

XRD of silica NP after calcination

Fig. 2

XRD of CuO NP after calcination

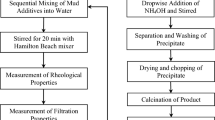
Preparation of drilling fluids

The following sequence and concentration by weight were used to prepare base NDDF:

$$500\, {\text{ml}}\;{\text{Tapwater}} + 2\% \,{\text{Polyamine}} + 0.1\% \,{\text{Biocide}} + 0.1\% \, {\text{Soda}}\,{\text{Ash}} + 0.3\% \,{\text{XCP}} + 2\% \,{\text{PACLV}} + 0.3\% \,{\text{PHPA}} + 6\% \,{\text{MCC}} + 26\% \,{\text{NaCl}}$$

The following sequence and concentration by weight were used to prepare base BDF:

$$500\,{\text{ml}}\; {\text{Tapwater}} + 4\, {\text{cp}}\,{\text{Bentonite}}\,{\text{gel}} + 0.5\% \,{\text{PACLV}} + {\text{Barite}}\,{\text{up}}\,{\text{to}}\, 1.10\,{\text{specific}}\,{\text{gravity}}$$

The following sequence and concentration by weight were used to prepare NP-based NDDF:

$$500\,{\text{ml}}\;{\text{Tapwater}} + {\text{Silica}}\,{\text{or}}\,{\text{Copper}}\,{\text{Oxide}}\,{\text{Nanoparticle}} + 2\% \,{\text{Polyamine}} + 1\% \,{\text{Biocide}} + 0.1\% \,{\text{Soda}}\,{\text{Ash}} + 0.3\% \,{\text{XCP}} + 2\% \,{\text{PACLV}} + 0.3\% \,{\text{PHPA}} + 6\% \,{\text{MCC}} + 26\% \,{\text{NaCl}}$$

The following sequence and concentration by weight were used to prepare NP-based BDF:

$$500\,{\text{ml}}\,{\text{Tapwater}} + {\text{Silica}}\,{\text{or}}\,{\text{Copper}}\,{\text{Oxide}}\,{\text{Nanoparticle}} + 4\,{\text{cp}}\,{\text{Bentonite}}\,{\text{gel}} + 0.5\% \,{\text{PACLV}} + {\text{Barite}}\,{\text{up}}\,{\text{to}}\, 1.10\,{\text{specific}}\,{\text{gravity}}$$

It is to be noted that samples of NP-based BDF and NP-based NDDF were prepared in varying concentrations of 0.5%, 0.8% and 1% by weight.

Following Table 1 shows the representation of prepared drilling fluids.

Table 1 Representation of prepared drilling fluid samples

Rheological measurements

The rheology test of each sample of drilling fluid was done by using a six speed Fann viscometer following API protocols. Stabilized shear stress values were recorded against different shearing rates at 600 rpm, 300 rpm, 200 rpm, 100 rpm, 6 rpm and 3 rpm.

The magnitude of plastic viscosity (PV, in centipoise) for each sample was calculated by measuring the difference of shear stress values at 600 rpm and 300 rpm. Yield points (YP) were calculated by measuring the difference between shear stress values at 300 rpm and PV for the specific sample. Initial gel strength (GS) or Gel 0 was measured by shearing the fluid at high speed and then allowing it to rest for 10 s. The maximum magnitude of shear stress reading at 3 rpm after the resting time was observed as initial GS or Gel 0. To measure the final GS or Gel 10, the same procedure was repeated except; the fluid was allowed to rest for 10 min. All the shear stress readings were expressed in lbs/100 ft². The same procedure to determine all rheological parameters was repeated after keeping the mud in an aging cell inside a hot roller oven for 16 h at 80 °C. These measurements gave an approximation about the alterations in the properties after the fluids were exposed to downhole temperatures.

Fluid loss measurements

Fluid loss or filtrate loss measurements were made in a OFITE API filtrate loss equipment. It consists of a metal cylinder with pressure seal rings. A 200 psi pressure was applied through a nitrogen cylinder from the top. Due to this differential pressure, the fluid is forced to pass through a filter paper placed at the bottom of the cylinder. The fluid lost through this filter paper is then collected in a test tube, where eventually volume of collected fluid is measured indicating filtrate or fluid loss.

Specific gravity and pH measurements

The specific gravity of the mud was measured using OFITE mud balance. The pH of the mud was measured by a digital pH meter. A typical range of pH for a drilling fluid should be between 8 and 10.

Results and discussion

Yield point

Yield point (YP) affects cutting carrying capacity of the drilling fluid. YP is measured in a Fann viscometer meter by assuming the rheological trend as Bingham plastic model and extrapolating the shear stress to a shear rate of zero. Hence, the YP from this type of rotational viscometer does not provide the magnitude of true yield nature of the fluid. Practically, a higher YP often contributes to higher frictional losses that consequently result in higher equivalent circulation density (ECD). A higher YP is often demanded in large diameter holes for efficient hole cleaning (Power and Zamora 2003). The YP for Bingham plastic model is given by:

$${\text{YP}} = \theta_{300} - {\text{PV}}$$

It was observed that the YP of NDDF increased with the increase in silica NPs concentration. Addition of 0.5% silica NP (S2) increased the YP of NDDF (S1) by 8%, while the addition of 1% silica NPs (S4) showed a significant increase in YP by 50 percent. Moreover, with the increase in temperature, fluids often showed a decrease in YP and viscosity. Likewise, S1 showed a reduction in YP by 22% when exposed to 80 °C. For S2, the margin of reduction was observed to be reduced to 14.7 percent. Furthermore, with the increase in concentration of silica NP, the magnitude of reduction was further scaled down by 2.7% for S3 and 5.2% for S4. Hence, it was concluded that along with the increase in magnitude of YP, silica NPs showed significant amount of temperature stability with the increase in their concentration. If this property persists for even higher values of temperature, it holds a lot of promise in the HP/HT conditions. For CuO NPs, maximum YP can be observed in 0.8% concentration, i.e., S5 which increased the YP of S1 by 17.5%. Addition of 0.5% (S5) and 1% CuO (S7) NPs concentration had an insignificant enhancement in YP, which was 4.7% and 1.5%, respectively. The concern with CuO NPs was that it showed less resistance after prolonged exposure (16 h) at high temperature (80 °C). With S1, the degradation in YP was observed to be 22.2%, while for S5, S6 and S7 it is increased to 39%, 45% and 31.3%, respectively. Contrasting observations were found for the scenario, where silica NPs were used with conventional BDF. No change in YP was found for S9, whereas the YP decreased with increase in concentration by 20% for S10 and 60% for S11. This occurrence might be due to agglomeration on silica NP on clay plates present in bentonite which resulted in a decrease in total electrostatic potential of the fluid. At high temperatures, the S8 had a degradation in YP, which was observed to be 20%, while for S9 and S10 the decreased was to 20% and 50%, respectively. With S11, no change was observed in the YP (Fig. 3).

Fig. 3

Yield point of all the prepared drilling fluid samples

The effects of CuO NPs on BDF were fairly constant. In fact, for both S12 and S13, CuO NP reduced the YP by 20%. No degradation in YP was observed for S12, while for S13 YP was reduced by 50% after hot roll (AHR) conditions. 1% by weight CuO NP (S14) had no effect on YP nature of the fluid but rather showed a detrimental effect at elevated temperature conditions by 40%. From the preceding observations, it can be inferred that for the case of NDDF, silica NPs, for an increasing doping concentration, shows an exponential rising trend in the yield point of the drilling fluid with the simultaneous development of an elevating resistance against temperature making it an ideal candidate for HP/HT conditions. For CuO NPs, for an increasing doping concentration, the rising trend of the yield point presents a nonlinear pattern. CuO NPs also lack a substantial resistance against increasing temperature and thus are not suitable for HP/HT conditions. Both silica and CuO NPs, when doped in BDF, show a substantial decrease in the yield point trend with the increase in concentration as well as temperature, leading them to be unfeasible for any high-temperature operations.

Viscosity

Viscosity is fundamentally resistance to flow. More solid content inherently increases the viscosity of a mud thereby making it thicker and conversely lesser solid content yields a thinner mud. Viscosity had a similar effect on ECD and pressure losses as YP. More ECD and more losses with an increase in viscosity often complicate normal proceedings while drilling. Moreover, with its increase, swab and surge pressures also intensify while tripping operation. If the increase in viscosity is due to increase in solid content, the drill string is more susceptible to a differential pipe sticking. Mud thickeners and mud thinners are used in the industry to increase and decrease the viscosity of a mud without much change in specific gravity (Figs. 4, 5).

Fig. 4

Plastic viscosity of all the prepared drilling fluid samples

Fig. 5

Apparent viscosity of all the prepared drilling fluid samples

The base NDDF showed a reduction in viscosities—both apparent and plastic with an increase in temperature. For S2, an increase in viscosity was observed by 5%. Furthermore, it was increased by 12.5% and 37.5% for S3 and S4, respectively. The NP-based NDDF showed a very interesting phenomenon where the viscosities increased with elevated temperature rather than conventional decrease. The driving principle behind this trend is unknown and yet to be investigated. This property had induced a thickening behavior with the increase in temperature rather than having a thinning effect on the drilling fluid. Unlike silica NPs, the effect of CuO NPs on both apparent and plastic viscosities did not follow a trend. For both S5 and S7, CuO NPs acted as thinners, while for S7 plastic viscosity marginally increased by 3.5% and apparent viscosity by 8.5%. The temperature stability of CuO NP in BDF also seemed to be an issue as it showed incapability to preserve the surface rheology. The addition of 0.5% silica NP for S9 had no effect on the base NDDF, whereas the viscosity was reduced by 25% for S10 and 50% for S11. Overall, the impact of silica NP with the increase in concentration on the viscosities of BDF was thinning. This observation can again be explained due to the fact that silica NPs tend to unite on the clay plates of bentonite and prevent the maintenance of attractive forces between clay plates. Like silica NPs, CuO NPs had a similar effect in the conventional drilling fluid in terms of viscosity, which was lowered with increase in concentration. This may have resulted due to deflocculating of clay plated as in case of silica NP-based drilling fluid. PV dropped by 25% for S13 with considerable temperature stability, while apparent viscosity was lowered by almost 24% for the same concentration. Mud thickening attribute of silica NP-doped NDDF was observed from increase of both apparent and plastic viscosities with the increase in NP concentration. Any similar result, however, was not observed with the doping of CuO NPs which presented an overall decreasing trend for both apparent and plastic viscosity with the increase in the NP concentration. The addition of silica NPs in BDF causes reduction in the viscosity of the drilling fluid to a great margin. The mud thinning behavior of silica NPs escalates with the gradual increase within its concentration. A similar trend is also observed with CuO NPs.

Gel strength

Gel strength is the measure of the shear stress at a very low shearing rate after the mud is left static for some time. It imparts the ability of a mud to suspend cuttings and weighted materials when there is a pause in circulation (Bern et al. 1996). In situations where excessive barite is used to cater to high pore pressure, it helps to counter barite sagging problems. An increase in gel strength can be observed due to the introduction of ultra-fine solids in the liquid phase, and in these conditions, more circulation pressure is needed to push the mud after a prolonged static condition (Figs. 6, 7).

Fig. 6

Gel strength (Gel 0) of all the prepared drilling fluid samples

Fig. 7

Gel strength (Gel 10) of all the prepared drilling fluid samples

Apart from observing an increase in gel strength with silica NP’s concentration, it also induced the property of thermal stability which aided to preserve the gel strength at bottom-hole conditions. This feature will assure proper suspension of rock cuttings and barite thereby preventing sagging issues. An increase in gel strength by 7.6% was observed only for S3, while all the other concentrations decreased the gel strength by a very small margin. The variation in gel strength after hot roll (AHR) was significant for S6, which decreased it by 27.2% for Gel 0 and 21.4% for Gel 10 measurements. 0.8% concentration for CuO NP shows maximum increase in gel strength for both the measurements indicating better cutting suspension. On the contrary, silica NPs had a detrimental effect on BDF. For this type of drilling fluid, it reduced the gel strength significantly in higher concentration as it is deflocculating in nature. The use of silica NPs is not recommended for high density muds as sagging issues might emerge due to low suspending capacity. CuO NPs did not have any effect on Gel 0 in both the conditions, while Gel 10 was reduced by 50%, 33% and 50% for S12, S13 and S14, respectively. Silica NPs when used with NDDF result in a nonlinear trend of the gel strength which produces the optimal strength maxima at 0.8% concentration. A similar while linear tread was observed with the addition of CuO NPs in NDDF with the maxima again at 0.8% concentration. A sharp decrease in gel strength was also observed in the CuO NPs-doped NDDF samples after hot rolling and aging. An exponentially detrimental trend was observed within BDF with the addition of silica NPs for all variants of NP concentration. An increasing trend was observed with the increase in the NP concentration in CuO NP.

API filtrate loss

The resultant pressure at any point in the wellbore is essentially outwards or directed toward the formation. This is due to the overbalance that persists throughout the operation to prevent kick or influx from the formation. This pressure forces the mud to invade the formation. The solid part of the mud forms a thin plaster around the wellbore, and the filtrate moves further into the formation. This filtrate loss if in shale formations can cause clay swelling or in production zone can alter the properties like wettability and relative permeability of the pay zone. These all contribute to further complexities and depreciating integrity of shale formation in the first case and in the later, production from a well (Mahto and Sharma 2004). Hence, minimizing the filtrate loss is of prime importance to impart smooth drilling operations or to avoid production problems (Figs. 8, 9).

Fig. 8

Fluid loss versus time of  S1–S7 

Fig. 9

Fluid loss versus time of S8–S14 

NDDF typically merged as a fluid loss control fluid, which prevents the contamination of the production zone or in shale sections clay swelling. For S2, the addition of 0.5% silica NPs reduced fluid loss by 31%, while for the S3 addition of 0.8% silica NPs reduced it by 58.6%. The fluid loss is best controlled for S4 by adding 1% silica NP that reduced it by 69%. This phenomenon takes place as the NPs block the pore spaces, which prevent to provide a clear passage for the fluid to pass through. But, in cases, with S3 and S4, the fluid loss increased in bottom-hole conditions due to excessive agglomeration of silica NPs. These agglomerations in higher concentration do not provide enough particles to block the pore throats. It was observed that S5 has a decrease in fluid loss at surface conditions by 31% when compared to S1. It also had a less reduction in fluid loss at bottom-hole condition by 17.5%. Similarly, for the S6 fluid loss was reduced by 13.8% at the surface condition and further reduction in fluid loss property in bottom-hole condition was restricted to 4% when compared to 29% for base S1 and 17.5% for S5, respectively. On the other hand, with the increase in concentration, the agglomeration of NPs prevailed, and hence, filtrate loss increased. This phenomenon was seen with S7, where the filtrate volume exceeded that of base NDDF by almost 3.4%. Silica NPs when used in conjunction with BDF provided a reduction in filtrate loss by 24% and 33% as seen with S9 and S10, respectively. Furthermore, an increase in filtrate loss by 8.7% was observed for S11. At bottom-hole conditions, the results were even more detrimental for S11 as it increased by 66%. This can be attributed to the fact that silica NPs tend to agglomerate at higher concentrations and due to overall viscosity reduction of the fluid. Apart from S12, which showed a decrease in filtrate loss by 24% (before hot roll) and 6.2% (after hot roll), furthermore, S13 and S14 showed increase in filtrate loss by 14.13% and 8.6%, respectively. These margins got worse with bottom-hole conditions as it increased to 30% and 41.6% when compared to filtrate loss in S8 (after hot roll). Hence, 0.5% concentration of CuO NPs (S12) seemed the best fit in reducing filtrate loss volume.

These observations inferred that NDDF when doped with silica NP presented a substantially decreasing trend of fluid loss of the mud with increase in concentration of the NP additive, whereas an increase in fluid loss was observed at the wellbore conditions. On the contrary, CuO NPs showed a detrimental trend of fluid loss decrease, where the volume of fluid loss decrease was reduced with the increase in the concentration of the NPs. A meagerly decreasing trend of fluid loss volume was observed with the addition of silica NPs in BDF at increasing concentrations, except at S11, where the fluid loss increased with the addition of NPs. S11 also failed in preventing fluid loss in bottom-hole conditions. Hence, silica NPs, at excessive concentration, are not worthy in terms of fluid loss control. A similar nonlinear trend was observed with addition of CuO NPs in BDF at increasing concentrations, where the local optimal concentration was obtained at 0.5% NP concentration.

Determination of optimal Herschel–Bulkley (HB) parameters by genetic algorithm optimization

Genetic algorithm (GA) is one of the most sought optimization algorithms, founded on the principle of continuous and autonomous evolutionary mechanism utilized to develop feasible process models for real and complex problems retaining optimal parameters. Existing since 1970s, the GA model has flourished under the guidance of John Holland, with the operating principle sharing its name (Saha et al. 2012). Based upon the idea of Darwin’s Natural Selection Theory, GA derives its foundation from the principal of genetic domination, and its relevance on forthcoming generations, which in the case of GA is the pareto-optimal domain. GA utilizes predefined biological constructs such as mutation, crossover, inheritance and selection in order to compute and refine the required range of optimal solutions. GA is also free from the major computational limitations such as linearity (Golberg 2001) and produces a set of problem-targeted optimal variants, devoid of any arbitrary and generalized constraints.

HB model proves to be most appropriate while examining the rheology of the drilling fluids; a major challenge associated with this model is the correct determination of the parameters: yield stress ($\tau_{o}$), fluid consistency index (k) and the flow index (n). The equation is given:

$$\tau = \tau_{o} + K\gamma^{n}$$

GA works via a simple process, to reduce the value of the objective function known as sum of squared errors (SSE) by the method of sequential genetic evolution and evaluation. The SSE is a direct indication of the deviation of the computed result of the selected parameters with relevance to the actual values. The process begins with the random initialization of the initial pool of parameters, limited within a selected preset of constraints. Over each iteration or ‘generation,’ evolved values of the parameters are devised and added to the generation pool. Each parameter’s trend is then evaluated over SSE which is given by:

$${\text{SSE}} = \mathop \sum \limits_{i = 1}^{6} \left( {\tau_{{{\text{obr}} .}} - \left( {\tau_{o} + K\gamma^{n} } \right)} \right)^{2}$$

A decreasing SSE trend allows the inclusion of that parameter into the next generation, whereas an increasing SSE trend causes the removal of that parameter from the next generation. This process is repeated until the specified number of generations is achieved, which in turn results in an array of feasible pareto-optimal fronts for the selected problem. Following Table 2 consists of the data.

Table 2 Optimal values of HB parameters by GA

Conclusion

This study is one of the first investigations of effect of NPs in NDDF. In this study, the use of silica NPs in NDDF has shown enough evidence to conclude that it enhances the rheological property as well as gives better fluid loss control in comparison with its effect when used with BDF. Silica NPs can emerge as an excellent fluid loss control agent when used in concentrations of 0.5% by weight as it yields minimum filtrate loss in the bottom-hole and surface conditions. At this prescribed concentration, it has least effect on its rheological properties as well, whereas the performance of 1% by weight of silica NPs in NDDF has shown mud thickening properties. Silica NPs when used with conventional BDF act as a mud thinner, which reduces the magnitude of rheological parameters. Apart from this, it also acts as a superior fluid loss agent in BDF at 0.5% by weight. Hence, it can be concluded that reduced concentrations of silica NPs (0.5% by weight) showed better results in both the fluids than in higher concentrations and showed less erratic behavior from the rheological standpoint. On the other hand, CuO NPs show thinning behavior when used in conjunction with NDDF. 1% by weight of CuO NP showed highest thinning effect, while 0.5% by weight showed superior fluid loss control. When used with conventional bentonite drilling fluid, addition of CuO NPs showed even greater thinning behavior. The viscosity of the fluid progressively decreased with increase in the concentration of CuO NPs. However, it is to be noted that the property of fluid loss control also deteriorates with increase in doping except for 0.5% by weight of CuO NPs’ concentration due to greater decrease in viscosity (Figs. 10, 11).

Fig. 10

Stress versus shearing rate of S1–S7

Fig. 11

Stress versus shearing rate of S8–S14