Introduction

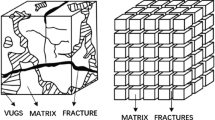
Carbonate formations are the most important type of hydrocarbon reservoirs. There are different data about global occurrence of this type of reservoirs (Akbar et al. 2000; Aljuboori et al. 2019; Bourbiaux 2010; Firoozabadi 2000; Schlumberger 2019); however, Akbar et al. (2000) estimated that about 60% of the world’s oil reserves lie in carbonate reservoirs. Aljuboori et al. (2019) reported from Schlumberger (2019) that 70% of conventional oil reserves in the Middle East lies in carbonate reservoirs. This type of reservoir could be considered more heterogeneous than sandstone reservoirs; especially, it is true if one considers their most important characteristic which is dual or even multiple porosity (permeability) feature. Secondary porous media appear as a result of basic diagenetic processes and fracturing (Lucia 2007; Ahr 2008; Moore 2001; Van Golf-Racht 1996). This heterogeneity causes some difficulties to efficiently manage production of carbonate reservoirs. To deplete a hydrocarbon reservoir in an efficient way, the operating company should have a good set of geologic and hydrodynamic data throughout the reservoir. The duality nature of carbonate reservoirs dictates to obtain the required data of both media. The acquired classical and common practice data are mainly characterizing matrix (first reservoir’s media). These data are usually obtained during well logging and well testing of drilled wells (Lucia 2007; Nelson 2001; Van Golf-Racht 1982; Heinemann and Mittermeir 2014). To fill gap of data between logged wells in a reservoir, geostatistical methods are available (Lucia 2007). To estimate properties of second media (fracture system), outcrop properties, electrical borehole scans, fractal discrete fracture network (FDFN) and analogy with other reservoirs are common methods (Kim and Schechter 2009). It is author’s experience that assigning outcrop properties to the reservoir could result a calamity in reality. On the other hand, it is author’s opinion that in the absence of a secondary porous system (in any form), majority of carbonate reservoirs are non-producing formations or at least their production would be uneconomical. So, it is crucial to estimate properties of this second porous media in a reliable way. The most confident data can be acquired from long-term dynamic behavior of a reservoir or/and a well. For this reason, in this paper, a procedure is presented to estimate well’s drainage radius and properties of a fracture system such as average length of matrix/fracture block, fracture porosity and fracture aperture from available long-term dynamic (production) data. This method is applied to a few wells of a real reservoir. The applied procedure is elaborated for one well in this work. For sake of confidentiality of data, the wells and reservoir are hereafter presented by letter ‘B.’

Summary of field data

Reservoir ‘B’ is a mid-sized structural carbonate with about 3000 MMSTB (million Stock Tank Barrel) oil in place which vertically consists of two separated parts. Initial reservoir pressure and bubble point pressure are reported to be around 6500 and 3200 psi, respectively. The produced crude oil gravity is reported to be around 32° API with solution gas–oil ratio (GOR) in the range of 1000–1200 SCF/STB. Initial oil formation volume factor is about 1.975 rbbl/STB. Oil viscosity at reservoir temperature and pressure is measured to be around 0.5 cP. Average porosity and water saturation are reported to be about 7 and 40 percent, respectively. The oil production rate of first drilled well is reported to be as much as 6000 STB/day (Stock Tank Barrel per day). Also, study of formation outcrops of this carbonate reservoir suggests that it could be well-fractured reservoir. Based on this initial data, it is predicted that the average sustainable production rate of future drilled wells could be up to 4000 STB/day. After putting the newly drilled wells on production, the average rate of wells gradually decreased to less than 1000 STB/day. Although no obvious sign of fractures has been detected during transient well testing of a few wells, core studies show some sort of micro-fractures. The pressure transient analysis of well test data revealed that permeability is in the range of 2–20 mD (millidarcy), while average air permeability of cores is reported to be around 0.01 mD.

The reservoir is at early stage of its depletion, and no aquifer is detected in the wells which drilled down to base of formation’s reservoir; so, drive mechanism of the reservoir is considered to be solution gas drive.

Data of well ‘B-1’ are used in the main text as an example of a comprehensive calculation with average permeability about 5 mD, estimated from well test. For a few other wells, a summary of results is presented in Table 1.

Table 1 Summary of obtained results by applied the procedure to a few wells
Full size table

Methodology

In this work, it is tried to estimate four main characteristics of fractured reservoir by using available long-term dynamic well production data. These properties are as follows:

  • Well drainage radius,

  • Matrix block height,

  • Fracture porosity,

  • Fracture aperture.

For estimation of well drainage radius, it is enough to assess amount of oil in place and then use average petrophysical data. Here, available and acceptable procedures such as decline curve analysis (DCA), inflow performance relationship (IPR) and material balance equation are integrated to compute the oil in place.

For calculation of matrix block height, it is assumed that producing oil in fractured reservoirs is mainly supplied by matrix and fissures are just conducting oil to wellbore, short time after putting well on production. From historical well’s production data, one can estimate average well production rate in interval period of time of investigation and also flowing bottom-hole pressure. By calculating theoretical rate of oil transfer from matrix to fissures in well drainage area for different matrix block heights and comparing to actual average well rate, the range of matrix block height can be estimated.

By employing equations presented by Reiss (1980) and Van Golf-Racht (1982) and estimated values for matrix block height, fracture width and fracture porosity can be assessed.

The details of this procedure are presented in the following sections by applying it to production data of well ‘B-1.’

Decline curve analysis (DCA)

One of the powerful tools for investigating a well (or reservoir) performance is decline curve analysis (DCA). By using this technique, ‘average oil rate’ and ‘expected cumulative oil production’ in desired period of time can be estimated. These two values are used in subsequent sections. ‘Expected cumulative oil production’ in conjunction with ‘estimated oil in place’ can be used to compute the percent of oil recovery. To rely on the estimated oil in place, this percent of computed oil recovery should be in acceptable range of recovery expected for the reservoir conditions. Also, ‘average oil rate’ is a factor which has been used to estimate matrix block height in corresponding section in this text.

The general equation for DCA is as follows (Arps 1945; Ahmed and McKinney 2005; Pratikno et al. 2003. Li and Horne 2003; Golan and Whitson 1996; Guo et al. 2007):

$$\frac{1}{q}\frac{{{\text{d}}q}}{{{\text{d}}t}} = - bq^{d}$$
(1)

where b and d are empirical constants to be determined based on production data. When d = 0, Eq. (1) is simplified to an exponential decline model, and when d = 1, Eq. (1) yields a harmonic decline model. When 0 < d < 1, Eq. (1) represents a hyperbolic decline model. The decline models are applicable to both oil and gas wells. For these three models, the following well performance relations are presented:

Exponential DCA

$$q = q_{\text{i}} {\text{e}}^{ - bt}$$
(2)
$$N_{\text{p}} = \frac{1}{b}\left( {q_{\text{i}} - q} \right)$$
(3)

Harmonic DCA

$$q = \frac{{q_{\text{i}} }}{1 + bt}$$
(4)
$$N_{\text{p}} = \frac{{q_{\text{i}} }}{b}\left( {\ln \left( {q_{\text{i}} } \right) - \ln \left( q \right)} \right)$$
(5)

Hyperbolic DCA

$$q = \frac{{q_{\text{i}} }}{{\left( {1 + dbt} \right)^{1/d} }}$$
(6)
$$N_{\text{p}} = \frac{a}{{b\left( {a - 1} \right)}}\left( {q_{\text{i}} - q\left( {1 - \frac{b}{a}t} \right)} \right)$$
(7)

‘Np,’ ‘qi’ and ‘a’ are cumulative well production, well rate at t = 0 and 1/d, respectively.

For model identification, Guo et al. (2007) recommended to plot the relative decline rate defined by Eq. (1) versus rate, see Fig. 1.

Fig. 1
figure 1

DCA model verification (Guo et al. 2007)

Full size image

Based on the model identification and available historical well data sets, it is verified that performance of all producers of ‘B’ reservoir obeys the exponential decline (see Fig. 2 for well ‘B-1’). For well ‘B-1,’ the best exponential equation fitted to the rate–time data is as follows:

$$q = 4013.8 \times {\text{e}}^{ - 0.0016t}$$
(8)

where ‘q’ and ‘t’ are well rate in STB/day and time in days, respectively. By integration of Eq. (8) or from chart of ‘cumulative—well rate’ (Fig. 2) and by limiting the minimum acceptable well rate equal to 100 STB/day, total cumulative oil production would be estimated to be around 2.45 MMSTB in the ‘first period of well life.’

Fig. 2
figure 2

DCA curves of well producer ‘B-1’

Full size image

Estimation of oil in place

Material balance is one method to estimate oil in place by using the data of production history. Details of this method are presented in nearly all reservoir engineering textbooks; among them, one can refer to Craft and Hawkins (1991), Donnez (2007), Ezekwe (2011), Slider (1983), Ahmed (2001) and Ahmed and McKinney (2005). For an undersaturated oil reservoir and by assuming volumetric performance, Ahmed and McKinney (2005) proposed the following equation for estimating oil in place:

$$N = \frac{{N_{\text{P}} B_{\text{o}} }}{{B_{\text{oi}} c_{\text{e}} \Delta P}}$$
(9)

where N, Np, Bo and Boi are initial oil in place, cumulative oil production, oil formation volume factor and initial oil formation volume factor, respectively. ΔP is initial reservoir pressure (Pi) minus current reservoir pressure (P). ce is effective fluid compressibility which is defined by Craft and Hawkins (1991) as follows (Ahmed and McKinney 2005):

$$c_{\text{e}} = \frac{{c_{\text{o}} S_{\text{o}} + c_{\text{w}} S_{\text{wi}} + c_{\text{f}} }}{{1 - S_{\text{wi}} }}$$
(10)

where co, cw and cf are oil, formation water and formation isothermal compressibility, respectively. So and Swi are oil saturation and initial water saturation, respectively.

Equation (9) can be rearranged to obtain a straight line equation relating reservoir pressure to cumulative production as follows:

$$P = P_{i} - \left( {\frac{1}{{NB_{\text{oi}} c_{\text{e}} }}} \right)N_{\text{P}} B_{\text{o}}$$
(11)

To employ Eq. (11) for estimation of oil in place, cumulative oil production and corresponding reservoir pressure are necessary. Cumulative oil production is usually reported in daily well production reports; however, reservoir pressure should be estimated from other measured data. In the following section, the employed procedure (inflow performance relationship, IPR) for estimating reservoir pressure is presented.

IPR of wells

Inflow performance relationship (IPR) is usually used to predict the potential well production especially for future performance of the well. In the simplest form of IPR, it is supposed that well rate is proportional to well’s down-hole drawdown. The proportionality factor is so-called productivity index (PI) which can be written as follows:

$${\text{PI}} = \frac{q}{{\left( {\bar{P}_{\text{r}} - P_{\text{wf}} } \right)}}$$
(12)

where ‘q’ is well rate in STB/day, and \(\bar{P}_{\text{r}}\) and Pwf are average reservoir pressure and bottom-hole well-flowing pressure in psi, respectively. PI is ‘Productivity Index’ in STB/day/psi. This equation can only be used for undersaturated oil reservoirs (Golan and Whitson 1996). The reservoir ‘B’ is undersaturated oil reservoir; however, to account for the possibility of non-Darcy flow around the wellbore, it is decided to use the Fetkovich relationship which can be employed both for oil and gas producer wells.

Inflow performance relationship (IPR) for oil well which is presented by Fetkovich (1973) is as follows (Golan and Whitson 1996; Guo et al. 2007; Ahmed 2001):

$$q = C\left( {\bar{P}_{\text{r}}^{2} - P_{\text{wf}}^{2} } \right)^{n}$$
(13)

where ‘q,’ \(\bar{P}_{\text{r}}\) and Pwf are defined as above. ‘C’ and ‘n’ are constants which should be estimated from well test data. To obtain these constants, it is necessary to flow the well at least at three different rates, successively. This test is also known as ‘flow after flow.’

Figure 3 illustrates the obtained IPR of well ‘B-1.’ The fitted trend line equation is as follows:

Fig. 3
figure 3

IPR of well ‘B-1’

Full size image
$$q = 0.0103\left( {\bar{P}_{\text{r}}^{2} - P_{\text{wf}}^{2} } \right)^{0.7942}$$
(14)

For future IPR equations, Fetkovich (1973) assumed that the coefficient ‘C’ in Eq. (13) linearly changes with average reservoir pressure (Ahmed and McKinney 2005), as shown in the following equation:

$$C_{\text{f}} = C_{\text{P}} \frac{{\left( {\bar{P}_{\text{r}} } \right)_{\text{f}} }}{{\left( {\bar{P}_{\text{r}} } \right)_{\text{P}} }}$$
(15)

where indices of ‘f’ and ‘P’ refer to future and current average reservoir pressures, respectively. Based on this concept and using Eqs. (14) and (15), IPR performance equation of producer well ‘B-1’ is obtained for different average ‘dynamic’ reservoir pressures. Author differentiates between average reservoir pressures in drainage area of a well when it is shut-in for a long period of time and when it is producing under pseudo-steady state; they can be called ‘static reservoir pressure’ and ‘dynamic reservoir pressure,’ respectively. It is especially true for dual-porosity reservoirs in which there is a great difference between the two individual media properties (such as permeability and porosity). In these types of reservoir, there is a ‘difference’ between well rate feeding by the secondary media and the amount of oil (gas) supplying by the first media (matrix). This will cause the average reservoir pressure ‘observed’ by well to be much less than the actual average reservoir pressure in the drainage area of the well.

To estimate the ‘average dynamic reservoir pressure’ from Eqs. (14) and (15), in addition to well flow rate ‘q,’ coefficients ‘n’ and ‘C,’ it is necessary to compute flowing bottom-hole pressure (Pwf) data. In daily well production data of well ‘B-1,’ flowing well head pressure data is available (Pt, tubing pressure). To convert ‘Pt’ data to Pwf, the well string performance for a set of flow rates is obtained by utilizing a professional well simulation software (PIPESIM). The results are shown in Fig. 4. From data of Fig. 4, production rate and flowing well head pressure (Pt), flowing bottom-hole pressure (Pwf) is estimated for historical production data. From these data and Eqs. (14) and (15), ‘average reservoir pressure’ for each period of time is estimated. Figure 5 depicts estimated ‘average dynamic reservoir pressure’ versus time for producer well ‘B-1.’

Fig. 4
figure 4

Vertical production string performance of producer well ‘B-1’

Full size image
Fig. 5
figure 5

Average dynamic reservoir pressure in drainage area of producer well ‘B-1’

Full size image

Estimated ‘dynamic reservoir pressure’ is plotted versus corresponding cumulative oil production for well ‘B1’ (see Fig. 6). Please notice that reported cumulative ‘surface’ oil production (Np) is converted to cumulative ‘reservoir’ oil production (NpBo); refer to Eq. (11). For this well, the slope of Eq. (11) is estimated to be as follows:

Fig. 6
figure 6

Estimation of oil in place in drainage area of producer well ‘B-1’

Full size image
$$\left( {\frac{1}{{NB_{\text{oi}} c_{\text{e}} }}} \right) = 5 \times 10^{ - 4}$$
(16)

From rock and fluid laboratory data, ‘effective compressibility’ and ‘initial oil formation volume factor’ are calculated as follows:

Boi = 1.975 rbbl/STB from laboratory-measured data.

Average oil compressibility (co) = 22 × 10−6 1/psi from laboratory-measured data.

Formation water compressibility = 2.3 × 10−6 1/psi at 4500 psi (salinity = 220,000 ppm, temperature = 247 °F); McCain (1990), Whitson (1994).

Average formation compressibility = cf = 7 × 10−6 1/psi at average 7% porosity, laboratory-measured data.

Initial water saturation = Swi = 40%, log data.

Oil saturation = So = 60%.

$$c_{\text{e}} = \frac{{c_{\text{o}} S_{\text{o}} + c_{\text{w}} S_{\text{wi}} + c_{\text{f}} }}{{1 - S_{\text{wi}} }} = \frac{{22 \times 10^{ - 6} \times 0.6 + 2.3 \times 10^{ - 6} \times 0.4 + 7 \times 10^{ - 6} }}{{\left( {1 - 0.4} \right)}} = 3.5 \times 10^{ - 5} {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\text{psi}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{psi}}$}}$$

Therefore, oil in place in the drainage area of producer well ‘B-1’ is estimated to be around 29 MMSTB, by inserting calculated values in Eq. (16). As ‘expected cumulative oil production’ is estimated to be around 2.45 MMSTB, see section Decline curve analysis (DCA), percent of oil recovery in drainage area of this well can be calculated to be around 8.45%. As the initial reservoir pressure is about 6500 psi, the computed percent of oil recovery could be said to be reasonable.

It is worthy to mention that deviation of production data from straight line in Fig. 6 shows that the drainage area of produced well ‘B-1’ does not behave as volumetric after producing about 2.0 MMrBBL equivalent to near 1.0 MMSTB. After this time (equivalent to 360 days), other reservoir energies such as oil feeding from outer well drainage area and potential aquifer are activated.

Estimation of drainage radius

By having an estimation of oil in place in the drainage area (about 29 MMSTB) and petrophysical data of well, it is possible to estimate drainage radius by using the following equation (for undersaturated oil reservoir):

$$N = \frac{1}{5.615} \times \pi r_{\text{e}}^{2} h \times \frac{{\emptyset \times \left( {1 - S_{\text{wi}} } \right)}}{{B_{\text{oi}} }}$$
(17)

where re and h are drainage radius and thickness of reservoir section both in ft, respectively. Other variables are defined as above. The magnitude of average porosity (ϕ), initial water saturation (Swi) and Boi is 0.07 (decimal), 0.4 (decimal) and 1.975 rbbl/STB, respectively, as mentioned in previous sections. Reservoir thickness in producer well ‘B-1’ is about 270 m (886 ft). Therefore, drainage radius is estimated to be about 1659 ft (506 m) from Eq. (17):

$$r_{\text{e}} = \sqrt {\frac{{29 \times 10^{6} \times 5.615 \times 1.975}}{{\pi \times 886 \times 0.07 \times \left( {1 - 0.4} \right)}}} = 1659\,{\text{ft}} = 506\,{\text{m}}$$

Estimation of matrix block height

Fracture flow dominates matrix flow in carbonate reservoirs (Van Golf-Racht 1996) owing to much higher fracture permeability than matrix permeability. Generally, in short term, well rate is relatively high as fractures are feeding the well; however, the reserve of fractures gradually depletes. At this time, the main source of oil production is matrix flow to fissures, and hereafter, fractures mainly conduit fluid from matrix to wellbore. So, in continuous long-term production from fractured carbonate reservoirs, the matrix to fracture flow becomes the main dominant factor of the well or reservoir production rate. One can find a long list of references in the literature which presented and discussed this matter (Van Golf-Racht 1982, 1996; Heinemann and Mittermeir 2014; Aljuboori et al. 2019). By utilizing basic concepts of flow from matrix to fracture, it is tried to estimate the matrix block dimensions, as follows.

To simulate the heterogeneous fractured carbonate reservoirs, various simplified idealized geometrical models are proposed by researchers (Reiss 1980; Van Golf-Racht 1982, 1996; Barenblatt et al. 1960; Kazemi 1969; Warren and Root 1963). Among them, two of the simple models are adopted for this study (Reiss 1980; Van Golf-Racht 1982, 1996). Figure 7 shows these selected two simples block models. To model flow from matrix to fissures, general linear steady-state flow is adopted as follows (Craft and Hawkins 1991; Ahmed 2001):

$$q = \frac{{0.001127\,kA\left( {P_{1} - P_{2} } \right)}}{{\upmu{\text{L}}}}$$
(18)

where q is the single matrix block flow rate to fracture, reservoir BBL/day, k: the matrix permeability, mD, A: the total area opened to flow from matrix to fracture, ft2, P1 and P2: the matrix and fracture dynamic pressure, psi, μ: the oil viscosity, cP, and L: the effective length of flow in matrix, ft.

Fig. 7
figure 7

Simple idealized geographic models used in this study

Full size image

By ignoring effect of the so-called block-to-block flow (Van Golf-Racht 1982; Saidi 1987; Shariat 2006; Lemonnier and Bourbiaux 2010), it is assumed that just one horizontal side of each matrix block has interaction fluid flow to fracture. To estimate total flow of matrix to fracture system in drainage area of the well, the following equation is utilized:

$$q_{\text{mf}} = \frac{{V_{\text{B}} }}{{v_{\text{mb}} }} \times \frac{q}{{B_{\text{o}} }}$$
(19)

where qmf is the total flow from matrix blocks to fracture system, STB/day, q: the single matrix block flow rate to fracture (Eq. 16), rbbl/day, VB: the bulk volume of drainage area, ft3, vmb: the single matrix block volume, ft3, and Bo: the oil formation volume factor, rbbl/STB.

By examining both idealized matrix blocks shown in Fig. 7, as flow from matrix to fracture is assumed to be taken place from one horizontal side, the results of both models are the same. So, the total flow from matrix blocks to fracture system, besides of other factors, depends on the height of matrix block in this study. Figure 8 depicts total flow from matrix blocks to fracture system versus matrix block height in drainage area of producer well ‘B-1.’ By considering historical average well flow in the range of 1500–3000 STB/day (refer to section ‘Decline curve analysis (DCA),’ and Fig. 1) and using Fig. 8, the height of matrix block can be estimated to be in the range of 75–240 ft depending on the average differential pressure between matrix and fracture (100–1000 psi).

Fig. 8
figure 8

Estimated average idealized matrix block height, producer well ‘B-1’

Full size image

Estimation of width and porosity of fractures

To estimate other fracture properties (porosity and width), equations presented by Reiss (1980) and Van Golf-Racht (1982) are employed. For detail of equations, reader is referred to mentioned references. By considering that vy = vz = 0.0, following equations are used:

$$A_{\text{fD}} = 1/a = {\text{Areal}}\;{\text{fracture}}\;{\text{density}},\left( {\text{cm}} \right).$$
(20a)
$$\emptyset_{\text{f}} = {\text{fracture}}\;{\text{porosity}} = \left( {96k_{\text{f}} A_{fD}^{2} } \right)^{0.33} ,\left( {\text{decimal}} \right).$$
(20b)
$$b = {\text{fracture}}\;{\text{width}} = \left( {\frac{{12k_{\text{f}} }}{{\emptyset_{\text{f}} }}} \right)^{0.5} ,\left( {\text{cm}} \right).$$
(20c)

Unit of fracture permeability (kf) in the above equations is cubic centimeter (cm2). As the estimated permeability in well tests (up to 5 mD) is about 500 times of measured permeability in laboratory (around 0.01 mD), it is assumed that the permeability of fracture is very close to that of obtained from well tests. Areal fracture density (Afd) is equal to reciprocal of length of matrix block which is in this text calculated as matrix block height in previous section.

So, based on the data of previous sections:

$$k_{\text{f}} = 5\,{\text{mD}} = 4.935 \times 10^{ - 11} \,{\text{cm}}^{2} ,$$
$$A_{\text{fD}} = 1/75\;{\text{to}}\;1/240\,{\text{ft}} = 4.37 \times 10^{ - 4} \;{\text{to}}\;1.37 \times 10^{ - 4} \,{\text{cm}}.$$

Thus:

$${\text{Fracture}}\;{\text{porosity}} = \phi_{\text{f}} = 1.09 \times 10^{ - 5} \;{\text{to}}\;5.0 \times 10^{ - 6} = 1.09 \times 10^{ - 3} \;{\text{to}}\;5.0 \times 10^{ - 4} \;{\text{percent}}.$$
$${\text{Fracture}}\;{\text{width}} = b = 7.4 \times 10^{ - 3} \;{\text{to}}\;1.08 \times 10^{ - 2} \,{\text{cm}} = 74\;{\text{to}}\;108\,\upmu{\text{m}}.$$

Discussion

For optimum reservoir management, characterizing rock and fluid properties is essential. For relatively homogeneous sandstone reservoirs, these properties can be assessed, in addition to transient well tests, by using conventional petrophysical well logs which measure static quantities and then assign them throughout the reservoir by geostatic techniques. In heterogeneous carbonate reservoirs with dual porous media, these standard methods are just applicable to matrix media. To estimate properties of second media (fracture system), outcrop properties, electrical borehole scans, fractal discrete fracture network (FDFN) and analogy with other reservoirs are common methods (Kim and Schechter 2009). However, if one can rely on accuracy of these types of data, they will just present reservoir properties at a short distance around the wellbore. For this reason, in this paper it is tried to present a procedure for characterizing fissures of a heterogeneous carbonate reservoir, from historical (dynamic) production data. By applying this procedure, one can estimate the matrix block height and fissures properties (porosity and aperture) in entire well’s drainage radius. This procedure, as elaborated in previous sections by applying it to a real case, can be summarized as follows:

  • A. Use decline curve analysis (DCA) technique to estimate the ultimate reserve in drainage area of each well.

  • B. Use well test data to find out the inflow performance relationship (IPR) of each well.

  • C. From IPR equation (section B), evaluate future IPR of the wells.

  • D. From future IPR and historical production data, estimate historical ‘average dynamic reservoir pressure’ in drainage area of the well.

  • E. From appropriate material balance equation, estimate oil in place in drainage radius of the well.

  • F. From average petrophysical properties of the well and part ‘E,’ estimate average drainage radius of the well.

  • G. By using the average historical well production rate, average matrix permeability and using simplified idealized geometrical matrix blocks, estimate the matrix block dimensions.

  • H. Use the equations presented by Reiss (1980) and Van Golf-Racht (1982), and estimate fracture width and fracture porosity.

This procedure is applied to historical production data of several wells, in addition to well ‘B-1.’ A summary of obtained results is presented in Table 1. One can adopt the concept of ‘radius of investigation’ to check the validity of calculated drainage radius presented in Table 1. One form of ‘radius investigation’ is as follows (Ahmed and McKinney 2005):

$$r_{\text{inv}} = 0.0325\sqrt {\frac{kt}{{\emptyset \mu c_{t} }}}$$
(21)

where t is the time, hr, k: the permeability, mD, and Ct: the total compressibility, 1/psi.

By considering this equation, it is supposed that the drainage radius should be proportional to square root of permeability or better to say a multiplication of permeability and time. Figure 9a presents plot of estimated drainage radius versus product of permeability and time. One data point which belongs to well ‘B-4’ is out of a proportionality. As it is mentioned, the reservoir consists of two separated vertical parts. To decrease the required producer wells, in a few wells such as ‘B-2’ and ‘B-4,’ both parts of reservoir section are perforated by the goal of comingled production of two parts of the reservoir. To distinguish the share of each part of the reservoir in production of these types of wells, production logging tools (PLTs) are run. The PLT results in well ‘B-4’ reveal that about 88 percent of production flows from just upper part of reservoir, during PLT test which conducted in early life of the well. It could be supposed that the share of this part in production of the well production gradually increased to about 100 percent by decreasing flowing down-hole pressure due to decrease in ‘average dynamic reservoir pressure’ in drainage radius of the well. If it is the case, the drainage area of well ‘B-4’ should be corrected to about 2384 ft instead of 1601 ft in Table 1. The plot of corrected data is shown in Fig. 9b. It should be noted that the drawn trend line (in Fig. 9b) just presents the proportionality and no other point. Other estimated characteristics of reservoir in the drainage area of this well (‘B-4’) are based on the new corrected value for drainage radius.

Fig. 9
figure 9

a Plot of drainage radius versus (kt), no correction. b Plot of drainage radius versus (kt), corrected data

Full size image

The calculated matrix block’s length is in the range of 50–240 ft for wells in Table 1. The magnitudes of this length for wells ‘B-1,’ ‘B-2’ and ‘B-4’ are very close to each other (see Table 1); however, the estimated value of matrix block height of well ‘B-3’ is much lower than the others. By looking at Table 1, it can be seen that although the permeability of well ‘B-3’ is much lower than that of well ‘B-1’ (2.3 mD vs. 5 mD), the average rate of well ‘B-3’ at end of investigated period is higher than that of well ‘B-1,’ 2500 STB/day and 1500 STB/day, respectively. If it is supposed that the fractures’ role is generally to conduct the reservoir’s fluid to the wellbore and the matrix is responsible for feeding the fractures, one can easily interpret the observed conflict of estimated properties of wells ‘B-1’ and ‘B-3.’ Lower matrix block height means higher number of matrix block per unit volume of drainage area. Consequently, it means higher surface area is available for fluid transfer from matrix to fissures. This hypothesis justifies the higher production rate of well ‘B-3,’ even though its permeability is lower than that of well ‘B-1.’

One point which a reservoir engineer should keep in mind is that when a hydrocarbon reservoir is put on production, it can no longer be considered as a static system and it should be treated as dynamic one. This means that reservoir engineer’s approach should be ‘a dynamic reservoir management’ and should continuously update estimated properties of the reservoir.

By applying this procedure to all producer wells with sufficient historical production data, one can provide a general map of width and porosity of fracture system throughout the reservoir. Also, by repeating this procedure during ‘efficient life’ of a well and comparison of estimated properties of fracture system in drainage area of well at ‘current time’ with those at ‘previous time,’ one can assess the effectiveness of previous well stimulation (for example, acid or hydraulic fracturing) and, also, estimate time of next well stimulation.

Conclusion and recommendation

By employing a straightforward procedure, a part of a heterogeneous carbonate reservoir is characterized. This procedure relies on all static and dynamic historical production data. From analysis of the data, it can be concluded that the reservoir under investigation is very tight. If one wants to simulate this reservoir as dual-porosity model, the secondary porosity media of this reservoir should be simulated as a micro-fracture media with its porosity around 0.005–0.0017 percent and fracture width in the range of 50–156 μm (micrometer). So, it is highly recommended to apply an efficient well stimulation such as acid or hydraulic fracturing to the well(s).

The presented procedure is an integrated dynamic reservoir characterization which in conjunction with the conventional-classical reservoir characterization can enhance petroleum engineer’s cognition and understanding of the reservoir under study. Based on the results and discussion, following points can be drawn:

  • Utilizing the results of running and conducting available tools and tests, in the field or laboratory, is necessary for reservoir characterization and, however, is not enough as they usually provide static data or/and dynamic information of a very small volume of the reservoir.

  • In a dual-media carbonate reservoir, ‘average dynamic reservoir pressure’ in drainage area of a well can be much lower than its ‘average static reservoir pressure.’ By increasing difference between properties of these two media, the difference between ‘dynamic’ and ‘static’ reservoir pressures increases.

  • It is ‘average dynamic reservoir pressure’ which governs production (injection) performance of a well.

  • Use ‘procedure’ presented in this paper to estimate the ‘average dynamic reservoir pressure’ in drainage area of active wells of a reservoir.

  • From ‘average dynamic reservoir pressure’ and other available reservoir’s fluid and rock properties, use the mentioned procedure to estimate matrix block sizes in the drainage area of the well.

  • Use the equations presented by Reiss (1980) and Van Golf-Racht (1982), and estimate fracture width and fracture porosity.

  • Prepare maps of matrix block size and fracture properties throughout of the reservoir by repeating the presented procedure for all active wells.

  • Repeat the procedure after each acid/hydraulic fracturing and compare the estimated properties with those obtained before this activity. This comparison will give an estimation of acid/hydraulic fracturing’s effectiveness.

  • Use the presented procedure to estimate drainage radius of all producer wells of interested reservoir. By mapping these estimated drainage radii, the areas that need to be drilled new wells can be located.