Radiation of sound in a semi-infinite hard duct inserted axially into a larger infinite lined duct

Abstract

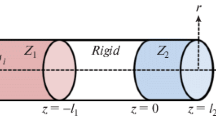
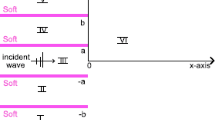
This article examines sound radiation from a hard semi-infinite duct placed symmetrically inside an acoustically lined duct. We introduce a wake on right handed region of the duct configuration to analyze sound radiation process for the trailing edge situation. The integral transforms together with Wiener–Hopf techniques render the solution of underlying problem. However expressions for field intensity involve infinite sums/products that enable solution using truncation approach. The sound radiation analysis is then observed graphically while using different choice of some pertinent parameters. It is worth mentioning that results of leading edge situation can be recovered as a limiting case.

Appendix

In order to separate all the functions of Wiener–Hopf functional equation in different half planes, kernel function is required to be factorized so that it is regular in different half planes and is free of singularities also. The factorization of the kernel functions $K(\alpha )$ and $W(\alpha )$ is of the form

$$\begin{aligned} K(\alpha )=K_{+}(\alpha )K_{-}(\alpha )\quad \text { and }\quad W(\alpha )=W_{+}(\alpha )W_{-}(\alpha ) \end{aligned}$$

where $K_{+}(\alpha )$ and $W_{+}(\alpha )$ denote certain functions which are regular and free of zeros in upper half plane $\mathrm{Im}\, \alpha >-\mathrm{Im}\,k$ and $K_{-}(\alpha )$ and $W_{-}(\alpha )$ denote certain functions which are regular and free of zeros in lower half plane $\mathrm{Im}\,\alpha <\mathrm{Im}\,k.$ It is noted that the functions $K(\alpha )$ and $W(\alpha )$ are even in $\alpha$ and more precisely their respective derivatives are zero at $\alpha =0.$ So these functions can be factorized by applying the infinite product expansion of an integral function with infinitely many zeros [20, 28]. From Eq. (35) we write $K(\alpha )$ as

$$\begin{aligned} K(\alpha )=\frac{\cos \kappa b-(\frac{{i}\zeta }{k})\kappa \sin \kappa b}{\kappa \sin \kappa a(\cos \kappa (b-a)-(\frac{{i}\zeta }{k})\kappa \sin \kappa (b-a))}. \end{aligned}$$

It is obvious that the product factorization of $K(\alpha )$ depends upon the factorization of

$$\begin{aligned} I(\alpha )= & {} \cos \kappa b-\left( \frac{{i}\zeta }{k}\right) \kappa \sin \kappa b,\\ L(\alpha )= & {} \cos \kappa (b-a)-\left( \frac{{i}\zeta }{k}\right) \kappa \sin \kappa (b-a), \end{aligned}$$

and

$$\begin{aligned} N(\alpha )=\kappa \sin \kappa a. \end{aligned}$$

Whilst using the procedure outlined by Mittra and Lee [29], it is found that

$$\begin{aligned} I(\alpha )= & {} \sqrt{\cos kb-{i}\zeta \sin kb}\exp \left\{ \frac{{i} \alpha b}{\pi }\left[ 1-C-\ln \left( \frac{\left| \alpha \right| b}{\pi }\right) +\frac{{i} \pi }{2}\right] \right\} \\&\times {\displaystyle \prod \limits _{n=1}^{\infty }} (1+\frac{\alpha }{\beta _{n}})\exp \left( \frac{{i}\alpha b}{n\pi }\right) ,\\ L(\alpha )= & {} \sqrt{\cos k(b-a)-{i}\zeta \sin k(b-a)}\nonumber \\&\times \,\exp \left\{ \frac{{i} \alpha (b-a)}{\pi }\left[ 1-C-\ln \left( \frac{\left| \alpha \right| (b-a)}{\pi }\right) +\frac{{i} \pi }{2}\right] \right\} \\&\times {\displaystyle \prod \limits _{n=1}^{\infty }} (1+\frac{\alpha }{\delta _{n}})\exp \left( \frac{{i}\alpha (b-a)}{n\pi }\right) , \end{aligned}$$

and

$$\begin{aligned} N(\alpha )= & {} \sqrt{k\sin ka}\exp \left\{ \frac{{i} \alpha a}{\pi }\left[ 1-C-\ln \left( \frac{\left| \alpha \right| a}{\pi }\right) +\frac{{i} \pi }{2}\right] \right\} \\&\times {\displaystyle \prod \limits _{n=1}^{\infty }} (1+\frac{\alpha }{\nu _{n}})\exp \left( \frac{{i}\alpha a}{n\pi }\right) . \end{aligned}$$

Thus

$$\begin{aligned} K(\alpha )=K_{+}(\alpha )K_{-}(\alpha ) \end{aligned}$$

where

$$\begin{aligned}&K_{+}(\alpha )=\sqrt{\frac{\cos kb-{i}\zeta \sin kb}{k\sin ka (\cos k(b-a)-{i}\zeta \sin k(b-a))}}\\&\quad \times \frac{\exp \left\{ \frac{{i} \alpha b}{\pi }\left[ 1-C-\ln \left( \frac{\left| \alpha \right| b}{\pi }\right) +\frac{{i} \pi }{2}\right] \right\} }{\exp \left\{ \frac{{i} \alpha a}{\pi }\left[ 1-C-\ln \left( \frac{\left| \alpha \right| a}{\pi }\right) +\frac{{i} \pi }{2}\right] \right\} \exp \left\{ \frac{{i} \alpha (b-a)}{\pi }\left[ 1-C-\ln \left( \frac{\left| \alpha \right| (b-a)}{\pi }\right) +\frac{{i} \pi }{2}\right] \right\} }\\&\quad \times {\displaystyle \prod \limits _{n=1}^{\infty }} \frac{(1+\frac{\alpha }{\beta _{n}})\exp \left( \frac{{i}\alpha b}{n\pi }\right) }{(1+\frac{\alpha }{\nu _{n}})\exp \left( \frac{{i}\alpha a}{n\pi }\right) (1+\frac{\alpha }{\delta _{_{n}}})\exp \left( \frac{{i}\alpha (b-a)}{n\pi }\right) }. \end{aligned}$$

Here $\beta _{n}^{,}s,\ \delta _{_{n}}^{,}s$ and $\nu _{n}^{,}s$ are the roots of the functions $I(\alpha ),$ $L(\alpha )$ and $N(\alpha ),$ respectively. That is

$$\begin{aligned} I(\beta _{n})=0, \quad L(\delta _{n})=0,\quad N(\nu _{n})=0 \quad n=1, 2, 3,\ldots \end{aligned}$$

with

$$\begin{aligned} I_{-}(\alpha )=I_{+}(-\alpha ),\quad L_{-}(\alpha )=L_{+} (-\alpha ),\quad N_{-}(\alpha )=N_{+}(-\alpha ) \end{aligned}$$

and C being the Euler’s constant given by $C=0.57721\ldots$ and $K_{-} (\alpha )=K_{+}(-\alpha )$. In the respective region of analyticity when $\left| \alpha \right| \rightarrow \infty$ we have

$$\begin{aligned} K_{\pm }(\alpha )=O(\left| \alpha \right| ^{-\frac{1}{2}}). \end{aligned}$$

For $W(\alpha )$ given by Eq. (42) we may write

$$\begin{aligned} W(\alpha )=\frac{\sin \kappa b+(\frac{{i}\zeta }{k})\kappa \cos \kappa b}{\kappa \cos \kappa a(\cos \kappa (b-a)-(\frac{{i}\zeta }{k})\kappa \sin \kappa (b-a))}. \end{aligned}$$

While opting a similar way, we get

$$\begin{aligned}&W_{+}(\alpha )=\sqrt{\frac{\sin kb+{i}\zeta \cos kb}{k\cos ka (\cos k(b-a)-{i}\zeta \sin k(b-a))}}\\&\quad \times \frac{\exp \left\{ \frac{{i} \alpha b}{\pi }\left[ 1-C-\ln \left( \frac{\left| \alpha \right| b}{\pi }\right) +\frac{{i} \pi }{2}\right] \right\} }{\exp \left\{ \frac{{i} \alpha a}{\pi }\left[ 1-C-\ln \left( \frac{\left| \alpha \right| a}{\pi }\right) +\frac{{i} \pi }{2}\right] \right\} \exp \left\{ \frac{{i} \alpha (b-a)}{\pi }\left[ 1-C-\ln \left( \frac{\left| \alpha \right| (b-a)}{\pi }\right) +\frac{{i} \pi }{2}\right] \right\} }\\&\quad \times {\displaystyle \prod \limits _{n=1}^{\infty }} \frac{(1+\frac{\alpha }{\widetilde{\beta }_{n}})\exp \left( \frac{{i} \alpha b}{n\pi }\right) }{(1+\frac{\alpha }{\widetilde{\nu }_{n}})\exp \left( \frac{{i}\alpha a}{n\pi }\right) (1+\frac{\alpha }{\delta _{_{n}}} )\exp \left( \frac{{i}\alpha (b-a)}{n\pi }\right) }. \end{aligned}$$

Here $\widetilde{\beta }_{n}^{,}s$ and $\widetilde{\nu }_{n}^{,}$ s are the roots of the functions

$$\begin{aligned} \frac{\sin \kappa b}{\kappa }+\left( \frac{{i}\zeta }{k}\right) \cos \kappa b=0, \end{aligned}$$

and

$$\begin{aligned} \cos \kappa a=0 \end{aligned}$$

respectively. Where C being the Euler’s constant given by $C=0.57721\ldots$ and $W_{-}(\alpha )=W_{+}(-\alpha )$. When $\left| \alpha \right| \rightarrow \infty$ then in the respective region of analyticity

$$\begin{aligned} W_{\pm }(\alpha )=O(\left| \alpha \right| ^{-\frac{1}{2}}). \end{aligned}$$