Introduction

Since it was invented by Japanese scientists in 1984 (Koizumi 1997), functionally graded materials (FGMs) are increasingly and widely used in many fields, such as aerospace, marine, mechanical, and structural engineering due to its advantages compared to classical fiber-reinforced laminated composites. The typical FGMs composed of ceramic and metal materials. The ceramic composition offers thermal barrier effects and protects the metal from corrosion and oxidation, and the metallic composition provides FGM toughness and strength.

For dynamic and static analysis of functionally graded plates and shells, many plate theories are developed. A review of shear deformation theories for isotropic and laminated plates was carried out by Ghugal and Shimpi (2002) and Khandan et al. (2012). Focus on modeling of functionally graded plates and shells, Thai and Kim (2015) reviewed various theoretical models to investigate their mechanical behavior. The classical plate theory (CPT) based on Kirchhoff assumptions and ignores the transverse shear deformation effect gives appropriate results for thin plates. First-order shear deformation theory (FSDT) takes into account the transverse shear deformation effect and needs a shear correction factor which is difficult to determine due to its dependence on many parameters. To overcome the weaknesses of FSDT, the higher order shear deformation theories are proposed.

A comprehensive review of the various methods employed to study the static, dynamic, and stability behavior of functionally graded plates can be found in work of Swaminathan et al. (2015). The review focuses on comparing the stress, vibration, and buckling characteristics of FGM plates using different theories. Based on third-order shear deformation theory with five displacement unknowns, Reddy (2000) developed analytical and finite-element solutions for static and dynamic analyses of functionally graded rectangular plates. El-Abbasi and Meguidin (2000) used a new thick shell element to study the thermoelastic behavior of functionally graded plates and shells. They extended the four-nodded seven-parameter shell element to account for the varying elastic and thermal properties, as well as the temperature boundary conditions on both faces of FG plates and shells.

Oyekoya et al. (2009) developed Mindlin-type element and Reissner-type element for the modeling of functionally graded plate subjected to buckling and free vibration. The Mindlin-type element formulation is based on averaging of transverse shear distribution over plate thickness using Lagrangian interpolation. The Reissner-type element formulation is based on parabolic transverse shear distribution over plate thickness using Lagrangian and Hermitian interpolation. Talha and Singh (2010) studied free vibration and static behavior of functionally graded plates using higher order shear deformation theory. A continuous isoparametric Lagrangian finite element with 13 degrees of freedom per node is employed for the modeling of functionally graded plates. Thai and Choi (2013) presented finite-element formulation of various four-unknown shear deformation theories for the bending and vibration analyses of functionally graded plates. To describe the primary variables, a four-node quadrilateral finite element is developed using Lagrangian and Hermitian interpolation functions. Three-dimensional graded finite-element method based on Rayleigh–Ritz energy formulation has been applied to study the static response of the thick functionally graded plates (Zafarmandand and Kadkhodayan 2014).

In this paper, a new higher order displacement field based on 12-unknown higher order shear deformation theory is developed to analyze the free vibration and buckling of functionally graded plates. The new eight-unknown higher order shear deformation theory is derived from the satisfaction of vanishing transverse shear stress at the top and bottom surfaces of the plate. The finite-element model is developed for bending and free vibration analysis of power-law functionally graded plates. A C1 continuous four-node quadrilateral plate element with 16 degrees of freedom per node is employed. Lagrangian linear interpolation functions are used to describe the in-plane displacements and the rotation of normals about x and y axes; Hermitian cubic interpolation functions are given for the transverse displacement, rotation about z-axis, higher order term of displacements and their first derivation.

Kinematics

The 12-unknown higher order displacement field is given as follows (Jha et al. 2012):

$$\begin{aligned} u\text{(}x\text{,}\;y,\;z\text{)}\; = \;u_{0} \text{(}x,\;y\text{)}\; + \;z\theta_{x} \text{(}x,\;y\text{)}\; + \;z^{2} u_{0}^{*} \text{(}x,\;y\text{)}\; + \;z^{3} \theta_{x}^{*} \text{(}x,\;y\text{)}; \hfill \\ v(x,\;y,\;z)\; = \;v_{0} (x,\;y)\; + \;z\theta_{y} (x,\;y)\; + \;z^{2} v_{0}^{*} (x,\;y)\; + \;z^{3} \theta_{y}^{*} (x,\;y); \hfill \\ w(x,\;y,\;z,\;t)\; = \;w_{0} (x,\;y,\;t)\; + \;z\theta_{z} (x,\;y,\;t)\; + \;z^{2} w_{0}^{*} (x,\;y,\;t)\; + \;z^{3} \theta_{z}^{*} (x,\;y,\,t) \hfill \\ \end{aligned}$$
(1)

where \(u,\;v,\;w\) denote the displacements of a point along the (x, y, z) coordinates. \(u_{0} , \, v_{0} , \, w_{0}\) are the corresponding displacements of a point on the midplane. \(\theta_{x}\), \(\theta_{y}\), and \(\theta_{z}\) are the rotations of the line segment normal to the midplane about the y-axis, x-axis, and z-axis, respectively. The functions \(u_{0}^{ * }\), \(v_{0}^{ * }\), \(w_{0}^{ * }\), \(\theta_{x}^{ * }\), \(\theta_{y}^{ * }\), and \(\theta_{z}^{ * }\) are the higher order terms in the Taylor series expansion defined in the midplane.

For bending plates, the transverse shear stresses \(\sigma_{xz}\) and \(\sigma_{yz}\) must be vanished at the top and bottom surfaces. These conditions lead to the requirement that the corresponding transverse strains on these surfaces be zero. From \(\gamma_{xz} \left( {x,\;y,\; \pm\frac{h}{2}} \right)\; = \;\gamma_{yz} \left( {x,\;y,\; \pm \frac{h}{2}} \right)\; = \;0\), we obtain

$$\begin{aligned} u_{0}^{*} \; = \; - \frac{1}{2}\theta_{z,x} \; - \;\frac{{h^{2} }}{8}\theta_{z,x}^{*} \text{;}\;\theta_{x}^{*} \; = \; - \frac{4}{{3h^{2} }}\left( {\theta_{x} \; + \;w_{0,x} } \right)\; - \;\frac{1}{3}w_{0,x}^{*} \text{;} \hfill \\ v_{0}^{*} \; = \; - \frac{1}{2}\theta_{z,y} \; - \;\frac{{h^{2} }}{8}\theta_{z,y}^{*} \text{;}\;\theta_{y}^{*} \; = \; - \frac{4}{{3h^{2} }}\left( {\theta_{y} \; + \;w_{0,y} } \right)\; - \;\frac{1}{3}w_{0,y}^{*} \text{.} \hfill \\ \end{aligned}$$
(2)

Thus, the displacement field (1) becomes

$$\begin{aligned} u\; = \;u_{0} \; + \;z\theta_{x} \; - \;\frac{{z^{2} }}{2}\left( {\theta_{z,x} \; + \;c_{1} \theta_{z,x}^{*} } \right)\; - \;\frac{{z^{3} }}{3}\left[ {c_{2} \left( {\theta_{x} \; + \;w_{0,x} } \right)\; + \;w_{0,x}^{*} } \right]; \hfill \\ v\; = \;v_{0} \; + \;z\theta_{y} \; - \;\frac{{z^{2} }}{2}\left( {\theta_{z,y} \; + \;c_{1} \theta_{z,y}^{*} } \right)\; - \;\frac{{z^{3} }}{3}\left[ {c_{2} \left( {\theta_{y} \; + \;w_{0,y} } \right)\; + \;w_{0,y}^{*} } \right]; \hfill \\ w\; = \;w_{0} \; + \;z\theta_{z} \; + \;z^{2} w_{0}^{*} \; + \;z^{3} \theta_{z}^{*} \hfill \\ \end{aligned}$$
(3a)

with \(c_{1} \; = \;\frac{{h^{2} }}{4};\;c_{2} \; = \;\frac{4}{{h^{2} }}\)

or in matrix notation as

$$\left\{ u \right\} = \left[ {\bar{H}} \right]\left\{ d \right\}$$
(3b)

where

$$\left[ {\bar{H}} \right]\; = \;\left[ {\begin{array}{*{20}c} 1 & 0 & {z\; - \;\frac{{c_{2} z^{3} }}{3}} & 0 & 0 & {\frac{{ - c_{2} z^{3} }}{3}} & 0 & 0 & {\frac{{ - z^{2} }}{2}} & 0 & 0 & {\frac{{ - z^{3} }}{3}} & 0 & 0 & {\frac{{ - c_{1} z}}{2}} & 0 \\ 0 & 1 & 0 & {z\; - \;\frac{{c_{2} z^{3} }}{3}} & 0 & 0 & {\frac{{ - c_{2} z^{3} }}{3}} & 0 & 0 & {\frac{{ - z^{2} }}{2}} & 0 & 0 & {\frac{{ - z^{3} }}{3}} & 0 & 0 & {\frac{{ - c_{1} z}}{2}} \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & z & 0 & 0 & {z^{2} } & 0 & 0 & {z^{3} } & 0 & 0 \\ \end{array} } \right] ;$$

\(\left\{ u \right\}\; = \;\left\{ {u ,\;v ,\;w} \right\}^{T}\) displacement vector of any generic point within the plate; \(\left\{ d \right\}\; = \;\left\{ {u_{0} ,\;v_{0} ,\;\theta_{x} ,\;\theta_{y} ,\;w_{0} ,\;w_{0,x} ,\;w_{0,y} ,\;\theta_{z} ,\;\theta_{z,x} ,\;\theta_{z,y} ,\;w_{0}^{*} ,\;w_{0,x}^{*} ,\;w_{0,y}^{*} ,\;\theta_{z}^{*} ,\;\theta_{z,x}^{*} ,\;\theta_{z,y}^{*} } \right\}^{T} .\)

Following strain–displacement relation, the non-zero strains are given as:

$$\left\{ {\begin{array}{*{20}c} {\varepsilon _{x} } \\ {\varepsilon _{y} } \\ {\varepsilon _{z} } \\ {\gamma _{{xy}} } \\ {\gamma _{{xz}} } \\ {\gamma _{{yz}} } \\ \end{array} } \right\}\;{\text{ = }}\;\left\{ {\begin{array}{*{20}c} {\varepsilon _{x}^{0} } \\ {\varepsilon _{y}^{0} } \\ {\varepsilon _{z}^{0} } \\ {\gamma _{{xy}}^{0} } \\ {\gamma _{{xz}}^{0} } \\ {\gamma _{{yz}}^{0} } \\ \end{array} } \right\}\; + \;z\left\{ {\begin{array}{*{20}c} {\kappa _{x}^{0} } \\ {\kappa _{y}^{0} } \\ {\kappa _{z}^{0} } \\ {\kappa _{{xy}}^{0} } \\ {\kappa _{{xz}}^{0} } \\ {\kappa _{{yz}}^{0} } \\ \end{array} } \right\}\; + \;z^{2} \left\{ {\begin{array}{*{20}c} {\varepsilon _{x}^{*} } \\ {\varepsilon _{y}^{*} } \\ {\varepsilon _{z}^{*} } \\ {\gamma _{{xy}}^{*} } \\ {\gamma _{{xz}}^{*} } \\ {\gamma _{{yz}}^{*} } \\ \end{array} } \right\}\; + \;z^{3} \left\{ {\begin{array}{*{20}c} {\kappa _{x}^{*} } \\ {\kappa _{y}^{*} } \\ 0 \\ {\kappa _{{xy}}^{*} } \\ {\kappa _{{xz}}^{*} } \\ {\kappa _{{yz}}^{*} } \\ \end{array} } \right\} \, {\rm or}: \left\{\varvec{\varepsilon}\right\}\; = \;\left\{ {\varvec{\varepsilon}^{{\mathbf{0}}} } \right\}\;\text{ + }\;\text{z}\left\{ {\varvec{\kappa}^{{\mathbf{0}}} } \right\}\; + \;z^{2} \left\{ {\varvec{\varepsilon}^{{\mathbf{*}}} } \right\}\; + \;z^{3} \left\{ {\varvec{\kappa}^{{\mathbf{*}}} } \right\}\text{.}$$
(4)

where

$$\left\{ {\varvec{\varepsilon}^{0} } \right\}\; = \;\left\{ {\varepsilon_{x}^{0} ,\;\varepsilon_{y}^{0} ,\;\varepsilon_{z}^{0} ,\;\gamma_{xy}^{0} } \right\}\; = \;\left\{ {u_{0,x} ,\;v_{0,y} ,\;\theta_{z} ,\;u_{0,y} \; + \;v_{0,x} } \right\};$$
$$\left\{ {\kappa_{x}^{0} ,\kappa_{y}^{0} ,\kappa_{z}^{0} ,\kappa_{xy}^{0} } \right\} = \left\{ {\theta_{x,x} ,\theta_{y,y} ,2w_{0}^{*} ,\theta_{x,y} + \theta_{y,x} } \right\};$$
$$\left\{ {\varepsilon_{x}^{*} ,\;\varepsilon_{y}^{*} ,\;\varepsilon_{z}^{*} ,\;\gamma_{xy}^{*} } \right\}\; = \;\left\{ { - \frac{1}{2}\left( {\theta_{z,xx} \; + \;c_{1} \theta_{z,xx}^{*} } \right){\kern 1pt} ,\; - \frac{1}{2}\left( {\theta_{z,yy} \; + \;c_{1} \theta_{z,yy}^{*} } \right),\;3\theta_{z}^{*} ,\; - \left( {\theta_{z,xy} \; + \;c_{1} \theta_{z,xy}^{*} } \right)} \right\};$$
$$\begin{aligned} \left\{ {\kappa_{x}^{*} ,\;\kappa_{y}^{*} ,\;\kappa_{xy}^{*} } \right\}\; = \;\left\{ { - \frac{1}{3}\left( {c_{2} \left( {\theta_{x,x} \; + \;w_{0,xx} } \right)\; + \;w_{0,xx}^{*} } \right)} \right.,\; - \frac{1}{3}\left( {c_{2} \left( {\theta_{y,y} \; + \;w_{0,yy} } \right)\; + \;w_{0,yy}^{*} } \right), \hfill \\ - \left. {\frac{1}{3}\left( {c_{2} \left( {\theta_{x,y} \; + \;\theta_{y,x} \; + \;2w_{0,xy} } \right)\; + \;2w_{0,xy}^{*} } \right)} \right\}; \hfill \\ \end{aligned}$$
$$\left\{ {\gamma_{xz}^{0} ,\;\gamma_{yz}^{0} } \right\}\; = \;\left\{ {w_{0,x} \; + \;\theta_{x} ,\;w_{0,y} \; + \;\theta_{y} } \right\};\;\left\{ {\kappa_{xz}^{0} ,\;\kappa_{yz}^{0} } \right\}\; = \;\left\{ { - c_{1} \theta_{z,x}^{*} ,\; - c_{1} \theta_{z,y}^{*} } \right\};$$
$$\left\{ {\gamma_{xz}^{*} ,\;\gamma_{yz}^{*} } \right\}\; = \;\left\{ { - c_{2} \left( {w_{0,x} \; + \;\theta_{x} } \right), - c_{2} \left( {w_{0,y} \; + \;\theta_{y} } \right)} \right\};\;\left\{ {\kappa_{xz}^{*} ,\;\kappa_{yz}^{*} } \right\}\; = \;\left\{ {\theta_{z,x}^{*} ,\;\theta_{z,y}^{*} } \right\}.$$

Constitutive equation

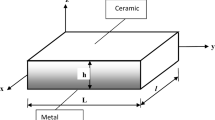
Consider a rectangular FGM plate with the length a, width b, and thickness h. The x-, y-, and z-coordinates are taken along the length, width, and height of the plate, respectively, as shown in Fig. 1. The material properties of FGM plates are assumed to vary continuously through the thickness of the plate by a power-law distribution as (Reddy 2002):

$$V(z)\; = \;\left( {V_{c} \; - \;V_{m} } \right)\left( {\frac{z}{h}\; + \;\frac{1}{2}} \right)^{p} \; + \;V_{m}$$
(5)
Fig. 1
figure 1

Geometry of FG plate with positive set of reference axes

Full size image

where V(z) represents the effective material property, such as Young’s modulus E, mass density ρ, and Poisson’s ratio ν; subscripts m and c represent the metallic and ceramic constituents, respectively; and p is the volume fraction exponent.

The stress–strain relationship for the FGM plate can be written as

$$\left\{ {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{y} } \\ {\sigma_{z} } \\ {\sigma_{xy} } \\ {\sigma_{xz} } \\ {\sigma_{yz} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & {Q_{13} } & 0 & 0 & 0 \\ {Q_{21} } & {Q_{22} } & {Q_{23} } & 0 & 0 & 0 \\ {Q_{31} } & {Q_{32} } & {Q_{33} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {Q_{44} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {Q_{55} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {Q_{66} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\varepsilon_{z} } \\ {\gamma_{xy} } \\ {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\}\;{\text{or compact matrix form}}\colon \;\left\{\varvec{\sigma}\right\}\; = \;\left[ \varvec{D} \right]\left\{\varvec{\varepsilon}\right\}$$
(6)

in which \(Q_{11} \; = \;Q_{22} \; = \;Q_{33} \; = \;\frac{{\left( {1\; - \;\nu } \right)E}}{{\left( {1\; + \;\nu } \right)\left( {1\; - \;2\nu } \right)}}\text{;}\) \(Q_{44} \; = \;Q_{55} \; = \;Q_{66} = \;\frac{E}{{2\left( {1\; + \;\nu } \right)}}\text{;}\)

$$Q_{12} = Q_{23} = Q_{13} = \frac{\nu E}{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}} = Q_{21} = Q_{32} = Q_{31} \text{.}$$

Finite-element formulation

A C1 continuous four-node quadrilateral plate-bending element with 16 degrees of freedom per node is used (Fig. 2). The Lagrangian linear interpolation functions \(N_{i} \left( {\xi ,\eta } \right)\) are employed to describe the variables \(u_{0} ,\;v_{0} ,\;\theta_{x} ,\;\theta_{y}\) and the Hermitian cubic interpolation functions \(H_{ij} \left( {\xi ,\;\eta } \right)\) are employed to describe the variables \(w_{0} ,\;w_{0,x} ,\;w_{0,y} {\mathbf{,}}\;\theta_{z} ,\;\theta_{z,x} ,\;\theta_{z,y} ,\;w_{0}^{*} ,\;w_{0,x}^{*} ,\;w_{0,y}^{*} ,\;\theta_{z}^{*} ,\;\theta_{z,x}^{*} ,\;\theta_{z,y}^{*}:\)

Fig. 2
figure 2

Node number of four-node quadrilateral element in its natural coordinate

Full size image
$$\left\{ {u_{0} ;\;v_{0} ;\;\theta_{x} ;\;\theta_{y} } \right\}^{T} \;{ = }\;\sum\limits_{i = 1}^{4} {N_{i} \left\{ {u_{0i} ;\;v_{0i} ;\;\theta_{xi} ;\;\theta_{yi} } \right\}^{T} \;} { = }\;\left[ {\bar{\varvec{B}}_{{\mathbf{1}}} } \right]\left\{ {\varvec{q}_{\varvec{e}} } \right\} ;$$
(7a)
$$\left\{ {w_{0} ;\;\theta_{z} ;\;w_{0}^{*} ;\;\theta_{z}^{*} } \right\}^{T} \; = \;\sum\limits_{i = 1}^{4} {\sum\limits_{j = 1}^{3} {H_{ij} \left\{ {w_{0i} ,\;w_{0i,x} ,\;w_{0i,y} ;\;\theta_{zi} ,\;\theta_{zi,x} ,\;\theta_{zi,y} ;\;w_{0i}^{*} ,\;w_{0i,x}^{*} ,\;w_{0i,y}^{*} ;\;\theta_{zi}^{*} ,\;\theta_{zi,x}^{*} ,\;\theta_{zi,y}^{*} } \right\}^{T} } \; = \;\left[ {\bar{\varvec{B}}_{{{\mathbf{21}}}} } \right]\left\{ {\varvec{q}_{\varvec{e}} } \right\}} ;$$
(7b)
$$\left\{ {w_{0,x} ;\theta_{z,x} ;w_{0,x}^{*} ;\theta_{z,x}^{*} } \right\}^{T} { = }\sum\limits_{i = 1}^{4} {\sum\limits_{j = 1}^{3} {H_{ij,x} \left\{ {w_{0i} ,w_{0i,x} ,w_{0i,y} ;\theta_{zi} ,\theta_{zi,x} ,\theta_{zi,y} ;w_{0i}^{*} ,w_{0i,x}^{*} ,w_{0i,y}^{*} ;\theta_{zi}^{*} ,\theta_{zi,x}^{*} ,\theta_{zi,y}^{*} } \right\}^{T} } { = }\left[ {\bar{\varvec{B}}_{22} } \right]\left\{ {\varvec{q}_{\varvec{e}} } \right\}} ;$$
(7c)
$$\left\{ {w_{0,y} ;\theta_{z,y} ;w_{0,y}^{*} ;\theta_{z,y}^{*} } \right\}^{T} { = }\sum\limits_{i = 1}^{4} {\sum\limits_{j = 1}^{3} {H_{ij,y} \left\{ {w_{0i} ,w_{0i,x} ,w_{0i,y} ;\theta_{zi} ,\theta_{zi,x} ,\theta_{zi,y} ;w_{0i}^{*} ,w_{0i,x}^{*} ,w_{0i,y}^{*} ;\theta_{zi}^{*} ,\theta_{zi,x}^{*} ,\theta_{zi,y}^{*} } \right\}^{T} } { = }\left[ {\bar{\varvec{B}}_{23} } \right]\left\{ {\varvec{q}_{\varvec{e}} } \right\}} .$$
(7d)

For rectangular elements, the interpolation functions \(N_{i}\) and \(H_{ij}\) for the ith node are given in terms of the natural coordinates as

$$N_{i} = \frac{1}{4}\left( {1 + \xi_{i} \xi } \right)\left( {1 + \eta_{i} \eta } \right) ;$$
(8a)
$$\begin{aligned} H_{i1} = \frac{1}{8}\left( {1 + \xi_{i} \xi } \right)\left( {1 + \eta_{i} \eta } \right)\left( {2 + \xi_{i} \xi + \eta_{i} \eta - \xi^{2} - \eta^{2} } \right) ,\hfill \\ {\text{H}}_{i2} = \frac{1}{8}\xi_{i} \left( {\xi_{i} \xi - 1} \right)\left( {1 + \eta_{i} \eta } \right)\left( {1 + \xi_{i}^{2} \xi^{2} } \right) ,\hfill \\ H_{i3} = \frac{1}{8}\eta_{i} \left( {\eta_{i} \eta - 1} \right)\left( {1 + \xi_{i} \xi } \right)\left( {1 + \xi_{i}^{2} \xi^{2} } \right) .\hfill \\ \end{aligned}$$
(8b)

\(\left\{ {q_{e} } \right\} = \left\{ {q_{{\mathbf{1}}} \text{,}\,q_{\text{2}} \text{,}\,q_{\text{3}} \text{,}\,q_{\text{4}} } \right\}^{T}\) is element nodal displacement vector.

\(\left\{ {q_{i} } \right\} = \left\{ {u_{0i} ,v_{0i} ,\theta_{xi} ,\theta_{yi} ,w_{0i} ,w_{0,xi} ,w_{0,yi} ,\theta_{zi} ,\theta_{z,xi} ,\theta_{z,yi} ,w_{0i}^{*} ,w_{0,xi}^{*} ,w_{0,yi}^{*} ,\theta_{zi}^{*} ,\theta_{z,xi}^{*} ,\theta_{z,yi}^{*} } \right\}^{T}\) is nodal displacement vector corresponding to the ith node.

The displacement vector at any generic point can be written as

$$\left\{ d \right\} = \left[ {\bar{B}} \right]\left\{ {q_{e} } \right\}$$
(9)

where \(\left[ {\bar{B}} \right] = \left[ {\left[ {\bar{B}_{1} } \right],\left[ {\bar{B}_{21} } \right],\left[ {\bar{B}_{22} } \right],\left[ {\bar{B}_{23} } \right]} \right]^{T}\) is the shape function matrix.

The strain vector is expressed by

$$\left\{ \varepsilon \right\} = \left[ L \right]\left\{ d \right\}\text{ = }\left[ L \right]\left[ {\bar{B}} \right]\left\{ {q_{e} } \right\} = \left[ B \right]\left\{ {q_{e} } \right\}.$$
(10)

[ L ] is differential operator matrix, \(\left[ B \right] = \left[ L \right]\left[ {\bar{B}} \right]\) is the strain–displacement matrix.

Hamilton’s principle can be expressed as

$$0 = \int\limits_{0}^{T} {\left( {\delta U + \delta W - \delta T} \right)} dt$$
(11a)

and applying for each element:

The strain energy of the FGM plate element is given by

$$U_{e} = \frac{1}{2}\int\limits_{{V_{e} }} {\left\{ \sigma \right\}}^{T} \left\{ \varepsilon \right\}dV = \frac{1}{2}\int\limits_{{V_{e} }} {\left\{ {q_{e} } \right\}^{T} \left[ B \right]^{T} \left[ D \right]} \left[ B \right]\left\{ {q_{e} } \right\}dV = \frac{1}{2}\left\{ {q_{e} } \right\}^{T} \left[ {K_{e} } \right]\left\{ {q_{e} } \right\}\text{.}$$
(11b)

The external work done on the plate element by distributed applied load may be written as

$$W_{e} = - \int\limits_{{A_{e} }} {\left\{ d \right\}}^{T} \left\{ f \right\}dA = - \int\limits_{{A_{e} }} {\left\{ {q_{e} } \right\}^{T} \left[ {\bar{B}} \right]^{T} \left\{ f \right\}} dA = - \left\{ {q_{e} } \right\}^{T} \left\{ {F_{e} } \right\}$$
(11c)

and {f} is mechanical load vector.

The kinetic energy of the FGM plate can be expressed as

$$T_{e} = \frac{1}{2}\int\limits_{V} {\left\{ {\dot{u}} \right\}}^{T} \left\{ {\dot{u}} \right\}\,\rho \text{(z)}dV = \frac{1}{2}\int\limits_{V} {\left\{ {\dot{q}_{e} } \right\}^{T} \left[ {\bar{H}} \right]^{T} \left[ B \right]}^{T} \left[ {\bar{H}} \right]\left[ B \right]\left\{ {\dot{q}_{e} } \right\}\,\rho \left( z \right)dV = \frac{1}{2}\left\{ {\dot{q}_{e} } \right\}^{T} \left[ {M_{e} } \right]\left\{ {\dot{q}_{e} } \right\}\text{.}$$
(11d)

Substituting Eqs. (11b–11d) into Eq. (11a), finite-element stiffness equation is obtained as

$$\left[ {M_{e} } \right]\left\{ {\ddot{q}_{e} } \right\} + \left[ {K_{e} } \right]\left\{ {{q}_{e} } \right\} = \left\{ {F_{e} } \right\}$$
(12)

where [K e ], [M e ], and {F e } are the element stiffness matrix, element mass matrix, and element nodal load vector, {q e } is nodal displacement vector, and \(\left\{ {\ddot{q}}_{e} \right\}\) is the second derivative of the displacements of the element with respect to time.

By assembling the element matrices, the global equilibrium equations for the plate can be obtained as

$$\left[ K \right]\left\{ Q \right\}{\mathbf{ + }}\left[ M \right]\left\{ {\ddot{Q}} \right\} = \left[ F \right].$$
(13)

where [K ], [M], and {F} are the global stiffness matrix, mass matrix, and nodal load vector of the structure, respectively, {Q} is nodal displacement vector, and \(\left\{ {\ddot{Q}} \right\}\) is the second derivative of the displacements of the structures with respect to time.

The generalized governing Eq. (13) can be employed to study the free vibration and static analysis by dropping the appropriate terms as follows.

For linear static analysis

$$\left[ K \right]\left\{ Q \right\} = \left\{ F \right\}.$$
(14)

For free vibration analysis, the frequency of natural vibration can be obtained from the bellow eigenvalue problem:

$$\left( {\left[ K \right]{\mathbf{ - }}\omega^{2} \left[ M \right]} \right)\left\{ Q \right\} = \left[ 0 \right].$$
(15)

This equation can be solved after imposing boundary conditions of the structure, with eigenvalues solving common problems.

The boundary conditions for an arbitrary edge with simply supported and clamped edge conditions are:

Clamped (C):

$$u_{0} = v_{0} = \theta_{x} = \theta_{y} = w_{0} = w_{0,x} = w_{0,y} = \theta_{z} = \theta_{z,x} = \theta_{z,y} = w_{0}^{*} = w_{0,x}^{*} = w_{0,y}^{*} = \theta_{z}^{*} = \theta_{z,x}^{*} = \theta_{z,y}^{*}$$

at x = 0; a and y = 0; b.

Simply supported (S):

\(v_{0} = \theta_{y} = w_{0} = w_{0,y} = \theta_{z} = \theta_{z,y} = w_{0}^{*} = w_{0,y}^{*} = \theta_{z}^{*} = \theta_{z,y}^{*}\) at x = 0; a.

\(u_{0} = \theta_{x} = w_{0} = w_{0,x} = \theta_{z} = \theta_{z,x} = w_{0}^{*} = w_{0,x}^{*} = \theta_{z}^{*} = \theta_{z,x}^{*}\) at y = 0; b.

Numerical results

Matlab codes for finite-element model have been built for numerical investigation. After checking convergence, a 10 × 10 mesh of four-node element has been used in the computation. The selective integration scheme based on Gauss-quadrature rules, with 3 × 3 for membrane, coupling, flexure and inertia terms and 2 × 2 for shear term. A rectangular FG plates with different boundary conditions, as shown in Fig. 3 are considered (F-free, S-simply supported, and C-clamped). Material properties of the P-FG plate are given in Table 1. For convenience, the following dimensionless forms are used (Thai and Kim 2013): \(\bar{w} = \frac{{10wE_{c} h^{3} }}{{q_{0} a^{4} }}\); \(\bar{\omega } = \omega h\sqrt {\frac{{\rho_{c} }}{{E_{c} }}} .\)

Fig. 3
figure 3

Boundary conditions of plates

Full size image
Table 1 Material properties used in the P-FG plate [13]
Full size table

Example 1

Validation study

Dimensionless central deflections \(\bar{w}\) of isotropic square plates (p = 0) with various values of thickness ratios a/h are presented in Table 2. The present results are compared with the solutions given by Thai and Choi (2013) based on four-unknown shear deformation theories (zeros shape function—FSDT) and the analytical solutions reported by Zenkour (2003) based on a mixed first-order shear deformation theory (MPT). It can be seen that the present solution is in close agreement with those solutions (errors <0.2%).

Table 2 Dimensionless deflection \(\bar{w}\) of isotropic square plates under uniform loads
Full size table

Dimensionless fundamental frequencies \(\bar{\omega }\) of simply supported (SSSS) square FG plates (p = 0) with various values of thickness ratios a/h and power-law index p are presented in Table 3. The comparison of the dimensionless fundamental frequencies of present results shows good agreement with analytical solutions of Thai and Kim (2013) based on simple higher order theory, and finite-element results of Thai and Choi (2013) based on four unknowns shear deformation theories.

Table 3 Dimensionless fundamental frequency \(\bar{\omega }\) of SSSS Al/Al2O3 square plates
Full size table

Example 2

Effect of power-law index p and side-to-thickness ratio a/h on the dimensionless central deflection \(\bar{w}\).

In this example, the square FG plate with different boundary conditions under uniformly distributed load is considered. The calculated dimensionless central deflection with various power-law indices p = 0; 0.5; 1.0; 2; 5; 10 and a/h = 5; 10; 20; 50 are given in Table 4. Figures 4 and 5 show the variation of power-law index p and side-to-thickness ratio a/h versus dimensionless central deflection. It is found that the dimensionless central deflection increases as power-law index p increases, while dimensionless central deflection decreases as side-to-thickness ratio increase with all types of boundary conditions.

Table 4 Dimensionless deflection \(\bar{w}\) of Al/Al2O3 square plates under uniform loads
Full size table
Fig. 4
figure 4

Variation of dimensionless deflection \(\bar{w}\) versus power-law index p of Al/Al2O3-1 square plates under uniform loads (a/h = 10)

Full size image
Fig. 5
figure 5

Variation of dimensionless deflection \(\bar{w}\) versus thickness ratio a/h of Al/Al2O3-1 square plates under uniform loads (p = 2)

Full size image

Example 3

Effect of power-law index p and side-to-thickness ratio a/h on the fundamental frequency \(\bar{\omega }\)

Table 5 presents the dimensionless fundamental frequency for various power-law indices p = 0; 0.5; 1.0; 2; 5; 10 and a/h = 5; 10; 20; 50. Different boundary conditions for each case are considered. The variation of dimensionless fundamental frequency versus power-law index p and side-to-thickness ratio a/h is illustrated in Figs. 6 and 7.

Table 5 Dimensionless fundamental \(\bar{\omega }\) frequency of Al/Al2O3 square plates
Full size table
Fig. 6
figure 6

Variation of dimensionless fundamental frequency \(\bar{\omega }\) versus power-law index p of Al/Al2O3 square plates (a/h = 10).

Full size image
Fig. 7
figure 7

Variation of dimensionless fundamental frequency \(\bar{\omega }\) versus thickness ratio a/h of Al/Al2O3 square plates (p = 2)

Full size image

It is observed that for all types of boundary condition, dimensionless frequencies decreases as power-law index and side-to-thickness ration increases. Effect of boundary conditions is clearly too, the dimensionless frequency of FG plate with boundary conditions CCCC is highest, and the lowest with SSSS boundary conditions.

Conclusions

In this study, the new eight-unknown shear deformation theory is used to analyze the bending and free vibration of rectangular functionally graded plates by finite-element approach. The governing equations and boundary conditions are derived by employing Hamilton’s principle. Validation studies have been carried out to confirm the accuracy of the present formulation. The obtained result shows good agreement with those available in the literature. Influence of power-law index, side-to-thickness ratio on bending, and vibration responses of FG plates have been investigated and discussed. The new eight unknowns shear deformation theory is accurate in predicting static and free vibration responses of FG plates.