An optimal policy for deteriorating items with time-proportional deterioration rate and constant and time-dependent linear demand rate

Abstract

In this paper, an economic order quantity (EOQ) inventory model for a deteriorating item is developed with the following characteristics:

• (i) The demand rate is deterministic and two-staged, i.e., it is constant in first part of the cycle and linear function of time in the second part.

• (ii) Deterioration rate is time-proportional.

• (iii) Shortages are not allowed to occur.

The optimal cycle time and the optimal order quantity have been derived by minimizing the total average cost. A simple solution procedure is provided to illustrate the proposed model. The article concludes with a numerical example and sensitivity analysis of various parameters as illustrations of the theoretical results.

Introduction

Most of the business organizations emphasize on inventory management and solving inventory problems because they want to obtain economic order quantity (EOQ) which minimizes the total average inventory cost. Over the last few decades, many researches have been done for controlling and maintaining the inventory. In real life situation, decay or deterioration of items is a natural phenomenon. Vegetables, fruits, foods, perfumes, chemicals, pharmaceutical, radioactive substances and electronic equipments, etc., are examples of deteriorating items, i.e., the loss characteristics of items at any time is regarded as deterioration. Therefore, it is not wise to ignore the factor deterioration while analyzing the model. Several inventory models for deteriorating items are developed to answer these questions: “How much to order to replenish the inventory of an item” and “When to order so as to minimize the total cost” (Gupta and Hira 2002).

The classical inventory model for deteriorating items of Harris (1915) and Wilson (1934) states that the depletion of inventory is mainly due to the constant demand rate. Firstly, the effect of deterioration on fashion items after their prescribed date was studied by Whitin (1957). Later, a dynamic version of the classical EOQ model for deteriorating items was developed by Wagner and Whitin (1958). Ghare and Schrader (1963) studied the inventory model for deteriorating items with constant deterioration rate and constant demand rate with the help of the differential equation $\frac{\mathrm{d}I\left( t\right) }{\mathrm{d}t}=-\theta I\left( t\right) -D\left( t\right) ,\,\,\,\,0\le t\le T$ where $I\left( t\right)$, $D\left( t\right)$ and $\theta$ represent the inventory level at any time t, the demand rate at time t and constant deterioration rate, respectively, during the cycle time T. Furthermore, the model for replenishment policies involving time-varying pattern has received much attention from several researchers. Donaldson (1977) examined the classical no-shortage inventory model for deteriorating items with a linear trend in demand over a known and finite horizon by using calculus method. An order-level inventory model for deteriorating items having constant deterioration rate was studied by Shah and Jaiswal (1977). Aggarwal (1978) modified the work of Shah and Jaiswal by calculating the average holding cost. Dave and Patel (1981) developed the inventory model for deteriorating items with linear increasing in demand rate and deterioration rate which was a constant fraction of the on-hand inventory. All the models discussed above are based on the constant deterioration rate, constant demand rate, infinite replenishment and no shortage. Heng et al. (1991) proposed an exponential decay in inventory model for deteriorating items by assuming a finite replenishment rate and constant demand rate. The reviews of the advances of deteriorating inventory literature are presented by Raafat (1991); Goyal and Giri (2001); Li et al. (2010); Bakker et al. (2012) and Janssen et al. 2016).

Goswami and Chaudhuri (1991) considered the replenishment policy for a deteriorating item with linear trend in demand rate. Xu et al. (1991) presented an inventory model for deteriorating items with linear demand rate over known and finite horizon. Chung and Ting (1994) proposed a heuristic inventory model for deteriorating items with time-proportional demand rate. Wee (1995) proposed a replenishment policy with exponential time-varying demand rate by extending the partial backlogging model. Benkherouf (1995) presented an optimal replenishment policy for a deteriorating item with known and finite planning horizon. The above models are based on constant deterioration rate and shortages. Srivastava and Gupta (2007) studied an EOQ model for deteriorating items with constant deterioration rate, both the constant and time-dependent demand rate and no-shortages.

In the real market situation, the state of demand rate of any product is always dynamic. Many researchers developed models by assuming time-dependent demand as linear, quadratic or exponential. However, linear demand, quadratic demand and exponential demand rates require uniform change, steady increase or decrease and rapid changes in demand rate, respectively. Chakrabarti and Chaudhuri (1997) studied a replenishment inventory problem for a deteriorating item over finite horizon with linear trend in demand rate. Singh and Pattnayak (2014) presented a two-warehouse inventory model with conditionally permissible delay in payment by considering linear demand rate. Ghosh and Chaudhuri (2004) developed an inventory model with two-parameter Weibull distribution deterioration rate, time-quadratic demand rate and shortages. Khanra et al. (2011) discussed an order-level inventory model for a deteriorating item with time-dependent quadratic demand rate and constant deterioration rate. The inventory models for deteriorating items with constant deterioration rate and exponential demand rate are established by Hollter and Mak (1983) and Ouyang et al. 2005).

Some more researches have been carried out on quantity discount, partial back-ordering, fuzzy environment of inventory system and delay in payments, etc. Widyadana et al. (2011) solved two EOQ models for deteriorating items inventory problems without using derivatives and found these as almost similar to the original model. Taleizadeh et al. (2013) solved a fuzzy rough EOQ model for deteriorating items considering quantity discount and prepayment by using meta-heuristic algorithms. Taleizadeh (2014) established an EOQ model for an evaporating item with partial back-ordering and partial consecutive prepayments. In this model, the retailers are allowed to pay all or a fraction of cost in advance. Thangam (2014) developed a two-level trade credit financing with selling price discount and partial order cancelations under permissible delay in payment. Taleizadeh et al. (2015) developed a production and inventory problem under two scenarios in a three-layer supply chain which involves one distributor, one manufacturer and one retailer. In this model, both defective items and raw materials with imperfect quality are sold at lower prices. Heydari and Norouzinasab (2015) studied a two-level discount inventory model for coordinating a decentralized supply chain considering demand as stochastic and price-sensitive.

Another class of researches on inventory model for deteriorating items was developed by considering the deterioration rate as time-proportional. Covert and Philip (1973) derived an EOQ model for deteriorating items without shortages under the condition of constant demand rate and two-parameter Weibull distribution deterioration rate. Philip (1974) generalized the model of Covert and Philip with same conditions by replacing two-parameter Weibull distribution by three-parameter Weibull distribution deterioration rate. Misra (1975) suggested an optimum production lot size inventory model for deteriorating items by including both constant and varying deterioration rate. Ghosh and Chaudhuri (2006) developed an EOQ model for a deteriorating item over a finite time-horizon by considering quadratic demand rate, time-proportional deterioration rate and by allowing shortages in all cycles. Mishra et al. (2013) developed an inventory model for deteriorating items with time-proportional deterioration rate, time-dependent linear demand rate and time-varying holding cost under partial backlogging. Sarkar and Sarkar (2013) considered an inventory model with variable deterioration rate and inventory dependent demand rate. Sanni and Chukwu (2013) developed an EOQ model for deteriorating items with ramp-type demand rate, three-parameter Weibull distribution deterioration after allowing shortages.

In classical inventory models, the deterioration rate and demand rate are assumed to be constant. But in reality, the demand is constant for some period of time and then it increases or decreases according to the popularity of the product. Furthermore, time is most important factor which plays an important role in developing the inventory model. As failure rate of some items increases with the passage of time, then the deterioration rate increases with respect to time. Therefore, the time-proportional deterioration rate is more realistic for the development of the model.

In this paper, an EOQ inventory model for deteriorating items is developed with time-proportional deterioration rate as well as both the constant and time-dependent linear demand rate. The demand for such products is constant for some time and after that, when the product becomes popular in the market, the demand for the product increases. A situation like this commonly occurs in practice. Shortages are not allowed to occur. The reason for considering the time-proportional deterioration rate and constant and time-dependent demand rate is due to the change in deterioration rate with respect to time and the suitable demand for the present market situation, respectively. It is assumed that items do not deteriorate at the beginning of the period, but the deterioration rate is time-proportional after some time with an increase in demand. The reason for considering constant and time-dependent demand rate instead of the time-dependent demand is due to the newly launched products like new branded android mobiles, automobiles, garments, etc. The demand for such products becomes constant initially and then increases. Shortages are not allowed to occur. In addition, the time-proportional deterioration rate is considered for the change in deterioration rate with respect to the time. The main objective of the model is to minimize the average total cost by optimizing the cycle time point. In addition, optimal order quantity is calculated. The solution procedure backed by a numerical example is provided to illustrate the proposed model. Finally, sensitivity of the solution with respect to various parameters associated with the model is studied.

The rest of the paper is organized as follows: the assumptions and notations for the development of the model are provided in Sects. 2 and 3, respectively. The formulation of the model is described in Sect. 4. In Sects. 5 and 6, solution procedure and a numerical example are presented to illustrate the developed model. In Sect. 7, sensitivity analysis with respect to various parameters is carried out. Finally, the summary and the future direction of research are given in Sect. 8.

Assumptions

To develop the proposed mathematical model of the inventory system, the following assumptions are considered in this paper:

• (i) The inventory system involves only one type of item.

• (ii) There is no deterioration for the first part of the cycle and the deterioration rate is time-proportional for the second part of the cycle.

• (iii) The demand is deterministic and has a two-component form for the time horizon, i.e., it is constant for the part of the cycle and is a linear function of time in the second part of the cycle.

• (iv) Shortages are not allowed to occur.

• (v) The occurrence of replenishment is instantaneous and the delivery lead time is zero.

• (vi) The planning horizon is infinite. Only a typical planning schedule of length is considered and all the remaining cycles are identical.

• (vii) Deteriorated units are not replaced or repaired during the cycle period under consideration.

• (viii) The ordering cost, holding cost and unit cost remain constant over time.

Notations

For convenience, the following notations are used throughout the paper.

$\theta \left( t\right)$::

The time-proportional deterioration rate, i.e., $\theta \left( t\right) =\theta _{0}t,$ where $0<\theta _{0}<<1$ and $t>0$. For $t=1$, the time-proportional deterioration rate reduces to a constant deterioration rate.

D(t)::

The varying demand rate, i.e., $D(t)=\left\{ \begin{array}{ll} a, &{}\quad 0\le t \le \mu , \\ a+b(t-\mu ), &{}\quad \mu \le t \le T. \end{array}\right.$

During the first interval $[0,\mu ]$, the demand is constant at the rate of a units per unit time, i.e., it does not vary with time and during the second interval $[\mu , T]$, the demand rate is a linear function of time.

I(t)::

The inventory level at any time t.

T::

The length of the replenishment cycle.

q::

The number of items received at beginning of the inventory system.

$c_{\mathrm{o}}$::

The ordering cost per order.

$h_{\mathrm{c}}$::

The inventory holding cost per unit per unit of time.

$d_{\mathrm{c}}$::

The unit cost of the item per unit per unit of time.

$\mu$::

The time point at which the demand increases with time as well as the deterioration starts.

$\mathrm{ATC}(T)$::

The average total cost per unit per unit time.

$T^{*}$::

The optimal value of T.

$q^*$::

The optimal value of q.

$\mathrm{ATC}(T^*)$::

The optimal average total cost per unit per unit time.

Mathematical formulation of the model

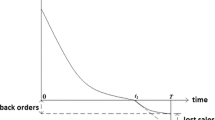
The cycle starts with the initial lot-size q at time $t=0$. During the time $[0,\mu ]$, the inventory level decreases due to the constant demand rate, say, a units per unit time. At time $t=\mu$, the depletion occurs due to the combined effect of demand and deterioration and finally comes to an end at time $t=T$. The behavior of the inventory system is depicted in the Fig. 1.

Fig. 1

The graphical representation of the inventory level with time

The objective of the model is to determine the optimal cycle length T that minimizes the average total cost $\mathrm{ATC}\left( T\right)$ over the time horizon [0, T].

During the interval $[0,\mu ]$, the demand rate is constant per unit time and is given by

$$\begin{aligned} a \end{aligned}$$

(4.1)

and thus, the total demand in the interval $[0, \mu ]$ is given by

$$\begin{aligned} a\mu . \end{aligned}$$

(4.2)

Therefore, the inventory level is reduced by the factor $a\mu$ and thus, the rest of inventory during $[\mu , T]$ is given by

$$\begin{aligned} q-a\mu . \end{aligned}$$

(4.3)

For the sake of mathematical simplicity, the interval $[\mu , T]$ can be written as

$$\begin{aligned} t_{1}=T-\mu . \end{aligned}$$

(4.4)

During the period $[\mu , T]$, the instantaneous inventory level $I\left( t\right)$ at any time t is governed by the following differential equation:

$$\begin{aligned} \frac{\mathrm{d}I\left( t\right) }{\mathrm{d}t}+\theta \left( t\right) I\left( t\right) =-\left[ a+b\left( t-\mu \right) \right] ,\,\,\,0\le t\le t_{1} , \end{aligned}$$

(4.5)

where $\theta \left( t\right) =\theta _{0}t,\quad (0<\theta _{0}<<1)$.

The solution of the differential Eq. (4.1) with boundary condition $I\left( 0\right) =q-a\mu$ is given by

$$\begin{aligned} I\left( t\right) =\left[ q-a\mu -a\left( t+\frac{\theta _{0}t^{3}}{6}\right) -b\left[ \frac{t^{2}}{2}+\frac{\theta _{0}t^{4}}{8}-\mu \left( t+\frac{\theta _{0}t^{3}}{6}\right) \right] \right] e^{-\frac{\theta _{0}t^{2}}{2}},\quad 0\le t\le t_{1} , \end{aligned}$$

(4.6)

by neglecting the higher power of $\theta _{0}$ as $0<\theta _{0}<<1$.

The Eq. (4.6) at $I\left( t_{1}\right) =0$ is given by

$$\begin{aligned} q=a\mu +a\left( t_{1}+\frac{\theta _{0}t_{1}^{3}}{6}\right) +b\left[ \frac{t_{1}^{2}}{2}+\frac{\theta _{0}t_{1}^{4}}{8}-\mu \left( t_{1}+\frac{\theta _{0}t_{1}^{3}}{6}\right) \right] . \end{aligned}$$

(4.7)

According to the assumptions of the model, the average total cost is composed of the following costs:

• I. The ordering cost (IOC):

  $$\begin{aligned} \mathrm{IOC}=c_{\mathrm{o}} \end{aligned}$$

  (4.8)

• II. The inventory holding cost (IHC) during the period [0, T] is calculated as follows:

  • 1. The of inventory holding cost during the period $[0, \mu ]$ is $h_{\mathrm{c}}\times$ area of trapezium ABCO, i.e.,

    $$\begin{aligned}&h_{\mathrm{c}}\left[ \frac{1}{2}\times \left( q+\left( q-a\mu \right) \right) \times \mu \right] \nonumber \\&\quad =\mu h_{\mathrm{c}}\left[ \left( q-a\mu \right) +\frac{a\mu }{2}\right] \end{aligned}$$

    (4.9)

    and

  • 2. The inventory holding cost during the period $[0, t_{1}]$ is $h_{\mathrm{c}}\times$ area of triangle BDC, i.e.,

    $$\begin{aligned} =h_{\mathrm{c}}\left[ \frac{1}{2}\times t_{1}\times \left( q-a\mu \right) \right] . \end{aligned}$$

    (4.10)

  Thus, the inventory holding cost (IHC) during the period [0, T] is the sum of inventory holding cost during the period $[0, \mu ]$ and inventory holding cost during the period $[0, t_{1}]$, i.e.,

  $$\begin{aligned} \mathrm{IHC}=h_{\mathrm{c}}\left[ \frac{a\mu ^{2}}{2}+\left( q-a\mu \right) \left( \mu +\frac{t_{1}}{2}\right) \right] . \end{aligned}$$

  (4.11)

• III. The deterioration cost (IDC) during the period [0, T] is

  $$\begin{aligned} \mathrm{IDC} &= d_{\mathrm{c}}\left[ q-a\mu -\int _{0}^{t_{1}}\left[ a+b\left( t-\mu \right) \right] \mathrm{d}t\right] \nonumber \\ &= d_{\mathrm{c}}\left[ q-a\mu -\left( a-b\mu \right) t_{1}-\frac{bt_{1}^{2}}{2}\right] . \end{aligned}$$

  (4.12)

Hence, the average total cost per unit time $(\mathrm{ATC}\left( T\right) )$ of the system during the period [0, T] expressed as the sum of the ordering cost, the inventory holding cost and the deterioration cost, i.e.,

$$\begin{aligned} \mathrm{ATC}\left( T\right)=\, & {} \frac{1}{T}\left[ \mathrm{IOC}+\mathrm{IHC}+\mathrm{IDC}\right] \nonumber \\ =\, & {} \frac{c_{\mathrm{o}}}{T}+\frac{a\left( T-\mu \right) }{T}\left[ 1+\frac{\theta _{0}\left( T-\mu \right) ^{2}}{6}\right] \left[ \frac{h_{\mathrm{c}}\left( T+\mu \right) }{2}+d_{\mathrm{c}}\right] \nonumber \\ &+\,\frac{b\left( T-\mu \right) }{T}\left[ \frac{\left( T-\mu \right) }{2}+\frac{\theta _{0}\left( T-\mu \right) ^{3}}{8}-\mu - \frac{\mu \theta _{0}\left( T-\mu \right) ^{2}}{6}\right] \left[ \frac{h_{\mathrm{c}}\left( T+\mu \right) }{2}+d_{\mathrm{c}}\right] \nonumber \\ &+\,\frac{1}{T}\left[ \frac{h_{\mathrm{c}}a\mu ^{2}}{2}- d_{\mathrm{c}}\left( a-b\mu \right) \left( T-\mu \right) -\frac{bd_{\mathrm{c}}\left( T-\mu \right) ^{2}}{2}\right] , \end{aligned}$$

(4.13)

by using Eqs. (4.4) and (4.7).

The objective of the problem is to determine the optimal value of T , i.e., $T^*$ such that $\mathrm{ATC}\left( T\right)$ is minimum.

For the optimum value of $\mathrm{ATC}\left( T\right)$, we have

$$\begin{aligned} \frac{\partial \mathrm{ATC}\left( T\right) }{\partial T}=0 \end{aligned}$$

(4.14)

and

$$\begin{aligned} \frac{{{\partial }^{2}}\mathrm{ATC}\left( T\right) }{\partial {{T}^{2}}}>0. \end{aligned}$$

(4.15)

From Eq. (4.14), we have

$$\begin{aligned} \frac{\partial \mathrm{ATC}\left( T\right) }{\partial T}=\, & {} \frac{a}{T}\left[ 1+\frac{\theta _{0}\left( T-\mu \right) ^{2}}{2}\right] \left[ \frac{h_{\mathrm{c}}\left( T+\mu \right) }{2}+d_{\mathrm{c}}\right] \nonumber \\ &+\,\frac{b}{T}\left[ T-2\mu +\frac{\theta _{0}\left( T-\mu \right) ^{3}}{2}-\frac{\mu \theta _{0}\left( T-\mu \right) ^{2}}{2} \right] \left[ \frac{h_{\mathrm{c}}\left( T+\mu \right) }{2}+d_{\mathrm{c}}\right] \nonumber \\ &+\,\frac{ah_{\mathrm{c}}\left( T-\mu \right) }{2T}\left( 1+\frac{\theta _{0}\left( T-\mu \right) ^{2}}{6}\right) \nonumber \\ &+\,\frac{bh_{\mathrm{c}}\left( T-\mu \right) }{2T}\left( \frac{\left( T-\mu \right) }{2}+\frac{\theta _{0}\left( T-\mu \right) ^{3}}{8}-\mu - \frac{\mu \theta _{0}\left( T-\mu \right) ^{2}}{6} \right) \nonumber \\ &-\,\frac{1}{T}\left[ d_{\mathrm{c}}\left( a-b\mu \right) +bd_{\mathrm{c}}\left( T-\mu \right) +\mathrm{ATC}\left( T\right) \right] =0 \end{aligned}$$

(4.16)

provided the sufficient condition

$$\begin{aligned} \frac{{{\partial }^{2}}\mathrm{ATC}\left( T\right) }{\partial {{T}^{2}}}>0. \end{aligned}$$

(See Appendix).

The solution procedure for above described model is given below.

Solution procedure: algorithms

To obtain the optimal value of $ATC\left( T\right)$ and q, the following steps are adopted.

• Step I. Put the appropriate value of the parameters.

• Step II. Determine the value of T from the Eq. (4.16) by Newton–Raphson method.

• Step III. Compare T with $\mu$.

  • (i) If $T>\mu$, then T is a feasible solution, say $T^{*}$. Go to Step IV.

  • (ii) If $T<\mu$, then T is infeasible.

• Step IV. Substitute $T^{*}$ in Eqs. (4.13) and (4.7) to get $ATC\left( T^{*}\right)$ and $q^{*}$, respectively.

Numerical example

To illustrate the results obtained from the inventory model for deteriorating items with two-component demand rate and time-proportional deterioration rate, the following numerical example is considered.

Example 1

Let us take the parametric values of the inventory model of deteriorating items in their units as follows:

$h_{\mathrm{c}}=\$0.50/\mathrm{unit}/\mathrm{day}$, $c_{\mathrm{o}}=\$80.0$, $d_{\mathrm{c}}=\$18.0/\mathrm{unit}$, $a=20\,\,\mathrm{units}$, $b=0.2$, $\mu =0.4\,\,\mathrm{days}$ and $\theta _{0} =0.02$.

Solving Eq. (4.16), the optimal cycle time is $T^{*}=2.73841$ days which satisfies the sufficient condition, i.e., $\frac{{{\partial }^{2}}\mathrm{ATC} \left( {{T}^{*}} \right) }{\partial {{T}^{2}}}=10.5991>0$. Substituting the value of $T^{*}=2.73841$ in Eqs. (4.13) and (4.7), the optimal value of the average total cost and the optimal order quantity are $\mathrm{ATC}\left( {{T}^{*}} \right) =\$48.9359$ and ${{q}^{*}}=55.9919$ units, respectively.

Sensitivity analysis

We now study the effect of changes in the values of various parameters $c_{\mathrm{h}}$, $c_{\mathrm{o}}$, $d_{\mathrm{c}}$, a, b, $\mu$ and $\theta _{0}$ on the optimum cost and optimum order quantity. The sensitivity analysis is performed by changing the each of the parameters by $+50$, $+25$, $+10$, $-10$, $-25$ and $-50\%$ taking one parameter at a time and keeping remaining parameters unchanged. The analysis is based on Example 1 and the results are shown in Table 1. The following points are observed.

• (i) $T^{*}$ increases while $\mathrm{ATC}\left( T^{*}\right)$ and $q^{*}$ decrease with the increase in the value of the parameter $h_{\mathrm{c}}$. Here $T^{*}$, $\mathrm{ATC}\left( T^{*}\right)$ and $q^{*}$ are moderately sensitive to changes in $h_{\mathrm{c}}$.

• (ii) $T^{*}$, $\mathrm{ATC}\left( T^{*}\right)$ and $q^{*}$ increase with the increase in the value of the parameter $c_{\mathrm{o}}$. Here $T^{*}$, $\mathrm{ATC}\left( T^{*}\right)$ and $q^{*}$ are highly sensitive to changes in $c_{\mathrm{o}}$.

• (iii) $T^{*}$ and $q^{*}$ decrease while $\mathrm{ATC}\left( T^{*}\right)$ increases with the increase in the value of the parameter $d_{\mathrm{c}}$. Here $T^{*}$, $\mathrm{ATC}\left( T^{*}\right)$ and $q^{*}$ are moderately sensitive to changes in $d_{\mathrm{c}}$.

• (iv) $T^{*}$ decreases while $\mathrm{ATC}\left( T^{*}\right)$ and $q^{*}$ increase with the increase in the value of the parameter a. Here $T^{*}$, $\mathrm{ATC}\left( T^{*}\right)$ and $q^{*}$ are highly sensitive to changes in a.

• (v) $T^{*}$ and $q^{*}$ decrease while $\mathrm{ATC}\left( T^{*}\right)$ increases with the increase in the value of the parameter b and $\theta _{0}$. Here $T^{*}$, $\mathrm{ATC}\left( T^{*}\right)$ and $q^{*}$ have low sensitivity to changes in b and $\theta _{0}$.

• (vi) $T^{*}$ and $q^{*}$ increase while $\mathrm{ATC}\left( T^{*}\right)$ decreases with the increase in the value of the parameter $\mu$. Here $T^{*}$, $\mathrm{ATC}\left( T^{*}\right)$ and $q^{*}$ have low sensitivity to changes in $\mu$.

Table 1 Sensitivity analysis

Table 2 Effect of parameter $\mu$ on optimal policies

From Table 2: It reveals that if the parameter $\mu$ is decreased by $87.5\%$, then the value of the optimal cycle time decreases by $4.62385\%$, the optimal average total cost increases by $6.28189\%$ and the optimal order quantity decreases by $3.54266\%$. Further, if the parameter $\mu$ is increased by $925\%$, then the value of the optimal cycle time increases by $52.1682\%$, the optimal average total cost decreases by $18.2471\%$ and the optimal order quantity increases by $48.7453\%$.

The notable point is that the increase in the value of the parameter $\mu$ after $\mu =4.10$ gives infeasible solution as $\mu >T$.

Conclusion

In this paper, an EOQ inventory model is developed for a deteriorating item with the two-staged demand rate, that is, it is constant at first part of the cycle and linear function of time at the second part of the cycle. The reason for considering constant and time-dependent linear demand rate is due to the newly launched products like new branded android mobiles, automobiles, garments, etc. The demand for such products remains constant initially and then increases. When a new product is launched in the market, the demand for such product becomes constant for some time and after that the demand increases due to the popularity of the product. Moreover, the time-proportional deterioration rate may be valid for the items whose deterioration rate changes with respect to time. It is assumed that items do not deteriorate at the beginning of the period, but after sometime, the deterioration rate increases with time. Deterioration rate is time-proportional. Shortages are not allowed to occur. The optimal cycle time and the optimal order quantity have been derived by minimizing the total average cost. A simple solution procedure is provided to illustrate the proposed model. The article is concluded with a numerical example and a sensitivity analysis of various parameters to support the theoretical results.

The proposed model can be extended in several ways. Firstly, we may extend the linear demand to a more generalized pattern that fluctuates with time, price or stock-demand rate. This idea can be extended for stochastic demand pattern too. Secondly, we could extend the model to variable deterioration rates like the two-parameter Weibull distribution deterioration rate and Gamma distribution deterioration rate. Finally, we could extend it by incorporating the concept of shortages or partial backlogging.

Appendix

$$\begin{aligned} \frac{{{\partial }^{2}}\mathrm{ATC}\left( T\right) }{\partial {{T}^{2}}}= & {} \frac{1}{T} \left[ a\theta _{0}\left( T-\mu \right) +b\left( 1+\frac{3\theta _{0}\left( T-\mu \right) ^{2}}{2}-\mu \theta _{0} \left( T-\mu \right) \right) \right] \left[ \frac{h_{\mathrm{c}}\left( T+\mu \right) }{2}+d_{\mathrm{c}}\right] \nonumber \\ &+\,\frac{h_{\mathrm{c}}}{T} \left[ a\left( 1+\frac{\theta _{0}\left( T-\mu \right) ^{2}}{2}\right) +b\left( T-2\mu +\frac{\theta _{0}\left( T-\mu \right) ^{3}}{2}-\frac{\mu \theta _{0}\left( T-\mu \right) ^{2}}{2}\right) \right] -\frac{bd_{\mathrm{c}}}{T}\nonumber \\ &-\,\frac{2}{T^{2}}\left[ a\left( 1+\frac{\theta _{0}\left( T-\mu \right) ^{2}}{2}\right) +b\left( T-2\mu +\frac{\theta _{0}\left( T-\mu \right) ^{3}}{2}-\frac{\mu \theta _{0}\left( T-\mu \right) ^{2}}{2}\right) \right] \left[ \frac{h_{\mathrm{c}}\left( T+\mu \right) }{2}+d_{\mathrm{c}}\right] \nonumber \\ &-\,\frac{h_{\mathrm{c}}\left( T-\mu \right) }{T^{2}}\left[ a\left( 1+\frac{\theta _{0}\left( T-\mu \right) ^{2}}{6}\right) +b\left( \frac{\left( T-\mu \right) }{2}+\frac{\theta _{0}\left( T-\mu \right) ^{3}}{8}-\mu -\frac{\mu \theta _{0}\left( T-\mu \right) ^{2}}{6}\right) \right] \nonumber \\ &+\,\frac{2d_{\mathrm{c}}}{T^{2}}\left[ a+b\left( T-2\mu \right) \right] +\frac{2\left( T-\mu \right) }{T^{3}}\left[ a\left( 1+\frac{\theta _{0}\left( T-\mu \right) ^{2}}{6}\right) \right. \nonumber \\ &\left. +\,b\left( \frac{\left( T-\mu \right) }{2}+\frac{\theta _{0}\left( T-\mu \right) ^{3}}{8}- \mu -\frac{\mu \theta _{0}\left( T-\mu \right) ^{2}}{6}\right) \right] \left[ \frac{h_{\mathrm{c}}\left( T+\mu \right) }{2}+d_{\mathrm{c}}\right] \nonumber \\ &+\,\frac{2}{T^{3}}\left[ \frac{h_{\mathrm{c}}a\mu ^{2}}{2}-d_{\mathrm{c}}\left( a-b\mu \right) \left( T-\mu \right) -\frac{bd_{\mathrm{c}}\left( T-\mu \right) ^{2}}{2}+\mathrm{ATC}\left( T\right) \right] . \end{aligned}$$