Mathematics Subject Classification 62E15, 62N05, 62F10, 60K10

Introduction

Burr [2] developed the system of Burr distributions. The Burr system of distributions includes 12 types of cumulative distribution functions which yield a variety of density shapes. The attractiveness of this relatively unknown family of distributions for model fitting is that it combines a simple mathematical expression for cumulative frequency function with coverage in the skewness–kurtosis plane. Many standard theoretical distributions, including the Weibull, exponential, logistic, generalized logistic, Gompertz, normal, extreme value, and uniform distributions, are special cases or limiting cases of the Burr system of distributions (see [11]). Family of Burr-type distributions is a very popular distribution family for modelling lifetime data and for modelling phenomenon with monotone and unimodal failure rates (see, for example, [13, 18]).

Analogous to the Pearson system of distributions, the Burr distributions are solutions to a differential equation, which has the form:

$$\begin{aligned} \frac{\mathrm{d}y}{\mathrm{d}x}=y(1-y)g(x,y), \end{aligned}$$
(1.1)

where y equal to F(x) and g(x, y) must be positive for y in the unit interval and x in the support of F(x). Different functional forms of g(x, y) result in different solutions F(x), which define the families of the Burr system. For example, Burr II distribution is obtained when \(g(x,y)=g(x)=\frac{ke^{-x}(1+e^{-x})^{k-1}}{(1+e^{-x})^k-1}\).

In this paper, we derive a new distribution of Burr-type distributions which is more flexible by replacing g(x, y) with \(g(x)=\frac{3px^2e^{-x^3}(1+e^{-x^3})^{p-1}}{(1+e^{-x^3})^p-1}\), (\(p>0\)). We refer to this new distribution as the new Burr distribution. If g(x, y) is taken to be g(x), then the solution of the differential Eq. 1.1 is given by

$$\begin{aligned} F(x)=(e^{-G(x)}+1)^{-1}, \end{aligned}$$
(1.2)

where \(G(x)=\int g(x) \mathrm{d}x\).

Hence, cdf and pdf of new Burr distribution are, respectively, given by

$$\begin{aligned} F(x;p)=(1+e^{-x^3})^{-p},-\infty<x<\infty ,(p>0), \end{aligned}$$
(1.3)

and

$$\begin{aligned} f(x;p)=3px^2e^{-x^3}(1+e^{-x^3})^{-p-1},-\infty<x<\infty . \end{aligned}$$
(1.4)

If the location parameter \(\mu\) and the scale parameter \(\sigma\) are introduced in the equation 1.3, we have

$$\begin{aligned} F(x;\mu ,\sigma , p)=(1+e^{-(\frac{x-\mu }{\sigma })^3})^{-p},-\infty<x<\infty ,(p,\sigma >0,\mu \in \mathbb {R}) \end{aligned}$$
(1.5)

and

$$\begin{aligned} f(x;\mu ,\sigma , p)=\frac{3p}{\sigma }\left( \frac{x-\mu }{\sigma }\right) ^2e^{-\left( \frac{x-\mu }{\sigma }\right) ^3}\left( 1+e^{-\left( \frac{x-\mu }{\sigma }\right) ^3}\right) ^{-p-1}. \end{aligned}$$
(1.6)

Hence, Eq. 1.5 is three parameter new Burr distribution. Hazard function associated with the new Burr distribution is

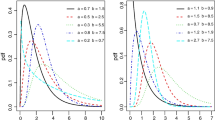
$$\begin{aligned} h(x;\mu ,\sigma , p)=\frac{\frac{3p}{\sigma }\left( \frac{x-\mu }{\sigma }\right) ^2e^{-\left( \frac{x-\mu }{\sigma }\right) ^3}\left( 1+e^{-\left( \frac{x-\mu }{\sigma }\right) ^3}\right) ^{-p-1}}{1-\left( 1+e^{-\left( \frac{x-\mu }{\sigma }\right) ^3}\right) ^{-p}}. \end{aligned}$$
(1.7)

The shapes of density and hazard functions of the new Burr distribution for different values of shape parameter p are illustrated in Fig. 1.

Fig. 1
figure 1

Graphs of density and hazard functions of the new Burr distribution for different values of shape parameter p

Full size image

New Burr distribution has unimodal and bimodal pdfs. None of the 12 types of Burr distributions has this feature. Data that exhibit bimodal behavior arises in many different disciplines. In medicine, urine mercury excretion has two peaks, see, for example, [5]. In material characterization, a study conducted by [4], grain size distribution data reveals a bimodal structure. In meteorology, [19] indicated that, water vapor in tropics, commonly have bimodal distributions. To see more applications of bimodal distributions, see [7–9, 16].

The reminder of the paper is organized as follows: properties of the new Burr distribution, such that moments, quantile functions, hazard function, Shannon’s entropy, and distribution of its order statistics are discussed in Sects. 2, 3, and 4. In Sect. 5, estimation of parameters and change-point of hazard function by the maximum likelihood method are discussed, and in Sect. 6, we establish a goodness-of-fit test statistic based on the Rényi Kullback–Leibler information for testing new Burr model. Finally, in Sect. 7, we present an illustrative example. Section 8 provides conclusions.

Properties of the new Burr distribution

New Burr distribution has unimodal and bimodal pdfs. The modes of distribution are provided by differentiating the density of new Burr distribution in 1.6 with respect to x:

$$\begin{aligned} f^{'}(x;\mu ,\sigma ,p)=3\left( \frac{x-\mu }{\sigma }\right) ^3\left( 1-pe^{-\left( \frac{x-\mu }{\sigma }\right) ^3}\right) -2\left( 1+e^{-\left( \frac{x-\mu }{\sigma }\right) ^3}\right) . \end{aligned}$$
(2.1)

The derivative \(f^{'}(x;\mu ,\sigma ,p)\) exists every where, hence critical point(s) satisfy equation \(f^{'}(x;\mu ,\sigma ,p)=0\). In 2.1, set \(\mu =0\) and \(\sigma =1\), because location and scale parameters will not affect the distribution shape. Thus, equation \(f^{'}(x;\mu ,\sigma ,p)=0\) simplifies to

$$\begin{aligned} 3x^3(1-pe^{-x^3})-2(1+e^{-x^3})=0. \end{aligned}$$
(2.2)

Analytical solution of 2.2 is not possible. Numerical approximation of modes using the midpoint method is applied to study the modes. The distance between the two modes is demonstrated in Table 1. From Table 1, it is observed that when p increases, the distance between two modes decreases, and for \(0<p<1\), when p decreases, value of pdf in the second mode decreases to zero and pdf will be almost unimodal, and for \(p=1\), values of pdf in two modes are the same but for \(p>1\), and when p increases, value of pdf in the first mode decreases to zero and pdf will be almost unimodal. Hence, the new Burr distribution can be used to analyse different kinds of lifetime data sets with unimodal and bimodal shapes of pdf.

Table 1 Distance between two modes of new Burr distribution
Full size table

The new Burr distribution has modified unimodal (unimodal followed by increasing) hazard function, and when p increases, hazard function will be almost increasing.

The main purpose in this paper is to describe and fit the data sets with non-monotonic hazard function, such as the bathtub, unimodal and modified unimodal hazard function. Many modifications of important lifetime distributions have achieved the above purpose, but unfortunately, the number of parameters has increased, the forms of survival and hazard functions have been complicated, and estimation problems have risen. More over some of the modifications do not have a closed form for their cdfs. However, this new distribution with one parameter and simple form of cdf achieves this purpose.

Now, we discuss the reverse hazard function of the new Burr distribution. The reverse hazard function of any distribution function F(x) can be defined as \(r(x)=\frac{f(x)}{F(x)}\). Consequently, the reversed hazard function of new Burr distribution with zero location parameter and unit scale parameter is given by

$$\begin{aligned} r(x;p)=\frac{3x^2e^{-x^3}}{1+e^{-x^3}}p. \end{aligned}$$

The reversed hazard function has recently attracted considerable interest of researchers (see, for example, [1, 3]). In a reliability setting, the reversed hazard function (multiplied by \(\mathrm{d}x\)) defines the conditional probability of a failure of an object in \((x-\mathrm{d}x,x]\) given that the failure had occurred in [0, x]. The reversed hazard function of new Burr distribution with zero location parameter and unit scale parameter is a linear function of p.

The rth moment about origin of the new Burr distribution is given by

$$\begin{aligned} \mu _ r=E(X^r)=\int _{-\infty }^{\infty }x^r\left( \frac{3p}{\sigma }\left( \frac{x-\mu }{\sigma }\right) ^2e^{-\left( \frac{x-\mu }{\sigma }\right) ^3}\left( 1+e^{-\left( \frac{x-\mu }{\sigma }\right) ^3}\right) ^{-p-1}\right) \mathrm{d}x, \end{aligned}$$

using the change of variable, \(t=\frac{1}{1+e^{-(\frac{x-\mu }{\sigma })^3}}\), \(0<t<1\), we obtain

$$\begin{aligned} E(X^r)= & {} \int _{0}^{1}pt^{p-1}\left( \sigma \left( -\ln \left( \frac{1}{t}-1\right) \right) ^{\frac{1}{3}}+\mu \right) ^r \mathrm{d}t \\=\; & {} p\left. \sum _{i=0}^{r}{r\atopwithdelims ()i}(-\sigma ) ^i\mu ^{r-i}\int _{0}^{1}pt^{p-1}\left( \ln \left( \frac{1}{t}-1\right) \right) \right) ^{\frac{i}{3}}\mathrm{d}t. \end{aligned}$$

Now, using \(\frac{1}{t}-1=e^u\), \(0<u<\infty\), we obtain

$$\begin{aligned} E(X^r)=\; & {} p\sum _{i=0}^{r}{r\atopwithdelims ()i}(-\sigma )^i \mu ^{r-i}\int _{0}^{\infty }(e^u+1)^{-p-1}u^{\frac{i}{3}}e^{u}\mathrm{d}u \\=\; & {} p\sum _{i=0}^{r}{r\atopwithdelims ()i}(-\sigma )^i \mu ^{r-i}E_q(g(X)), \end{aligned}$$

where \(E_q(.)\) denotes expectation for \(X\sim q\) and q is the standard exponential distribution and \(g(x)=(e^x+1)^{-p-1}x^{\frac{i}{3}}e^{2x}\). Using the importance sampling method, the importance sampling estimate of \(\mu _r\) is given by

$$\begin{aligned} \hat{\mu _ r}_q=p\sum _{i=0}^{r}{r\atopwithdelims ()i}(-\sigma )^i \mu ^{r-i}\left( \frac{1}{n}\sum _{k=1}^{n}g(X_k)\right) , \quad X_k\sim q. \end{aligned}$$
(2.3)

Using \(n=1000\), the importance sampling estimate of mean and variance of the new Burr distribution as \(\mu =0\) and \(\sigma =1\) for different values of p is demonstrated in Table 2. From Table 2, it is observed that when p increases, mean increases and variance decreases. Mean and variance \(\hat{\mu _ r}_q\) are given by

$$\begin{aligned} E(\hat{\mu _ r}_q)=\mu _ r,\mathrm{var} (\hat{\mu _ r}_q)=p^2\sum _{i=0}^{r}\left( {r\atopwithdelims ()i}(-\sigma )^i \mu ^{r-i}\right) ^2 \mathrm{var} (\hat{E_q }(g(X))), \end{aligned}$$

where \(\mathrm{var} (\hat{E_q} (g(X)))=E_q ((g(X)-E_q(g(X)))^2)\).

To form a confidence interval for \(\mu _r\), we need to estimate \(\mathrm{var} (\hat{E_q} (g(X)))\). Because \(X_k\) are sampled from q, the natural variance estimate is

$$\begin{aligned} \hat{\mathrm{var}} (\hat{E_q} (g(X)))=\frac{1}{n}\sum _{k=1}^{n} (g(X_k)-\hat{E_q }(g(X)))^2. \end{aligned}$$

Then, an approximate 99% confidence interval for \(\mu _r\) is \(\hat{\mu _ r}_q\pm 2.58 \frac{\hat{\mathrm{var} }(\hat{\mu _r}_q)}{\sqrt{n}}\).

Table 2 Importance sampling estimate of mean and variance of the new Burr distribution
Full size table

The quantile function, Q(u), \(0<u<1\), for the new Burr distribution can be computed using the formula:

$$\begin{aligned} Q(u)=\sigma \left( -\ln \left( u ^{-\frac{1}{p}}-1\right) \right) ^{\frac{1}{3}}+\mu . \end{aligned}$$

The median of a new Burr distribution occurs at \(\sigma (-\ln ((\frac{1}{2})^{-\frac{1}{p}}-1))^{\frac{1}{3}}+\mu\), and clearly, it is a decreasing function of p as \(p\le 1\) but an increasing function of p as \(p\ge 1\).

Skewness and kurtosis of a parametric distribution are often measured by \(\alpha _3=\frac{\mu _3}{\sigma ^3}\) and \(\alpha _4=\frac{\mu _4}{\sigma ^4}\), respectively. When the third or fourth moment does not exist, for example, Cauchy, Lévy, and Pareto distributions, \(\alpha _3\) and \(\alpha _4\), cannot be computed. For the new Burr distribution, skewness and kurtosis can be approximated by approximations of \(\mu _3\) and \(\mu _4\) or alternative measures for skewness and kurtosis, based on quantile functions. The measure of skewness S defined by [6] and the measure of kurtosis K defined by [12] are based on quantile functions and they are defined as

$$\begin{aligned} S= & {} \frac{Q\left( \frac{6}{8}\right) -2Q\left( \frac{4}{8}\right) +Q\left( \frac{2}{8}\right) }{Q\left( \frac{6}{8}\right) -Q\left( \frac{2}{8}\right) }, \end{aligned}$$
(2.4)
$$\begin{aligned} K= & {} \frac{Q\left( \frac{7}{8}\right) -Q\left( \frac{5}{8}\right) +Q\left( \frac{3}{8}\right) }{Q\left( \frac{6}{8}\right) -Q\left( \frac{2}{8}\right) }. \end{aligned}$$
(2.5)

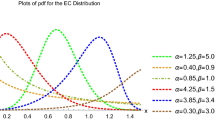
To investigate the effect of the shape parameter p on the new Burr density function, Eqs. 2.4 and 2.5 are used to obtain Galton’s skewness and Moors’ kurtosis. Figure 2 displays the Galton’s skewness and Moors’ kurtosis for the new Burr distribution in terms of the parameter p when \(\mu =0\) and \(\sigma =1\).

Fig. 2
figure 2

Galton’s skewness and Moors’ kurtosis for the new Burr distribution

Full size image

Shannon’s entropy

The entropy of a random variable X is a measure of variation of uncertainty. Shannon’s entropy [17] for a random variable X with pdf f(x) is defined as \(E(-\log (f(x)))\). In recent years, Shannon’s entropy has been used in many applications in fields of engineering, physics, and economics.

Denote by \(H_{sh}(X)\) the well-known Shannon’s entropy. The following theorem gives the Shannon’s entropy of the new Burr distribution.

Theorem 3.1

The Shannon’s entropy of the new Burr distribution is given by

$$\begin{aligned} H_{sh}(X)= & {} -\ln \frac{3p}{\sigma }-\frac{2p}{3}\sum _{i=0}^{\infty }{-p-1\atopwithdelims ()i}\left( \frac{\Gamma ^{'}(1)-\ln (p+i)}{p+i}\right) \\&-p\sum _{i=0}^{\infty }{-p-1\atopwithdelims ()i}\frac{1}{(p+i)^2}+\frac{1}{p}+1. \end{aligned}$$

Proof

$$\begin{aligned} H_{sh}(X)= & {} -\int _{-\infty }^{\infty }f(x)\ln f(x) \mathrm{d}x=-\ln \frac{3p}{\sigma }-2E\left( \ln \left( \frac{X-\mu }{\sigma }\right) \right) \nonumber \\&+\;E\left( \left( \frac{X-\mu }{\sigma }\right) ^3\right) +(p+1)E\left( \ln \left( 1+e^{-\left( \frac{X-\mu }{\sigma }\right) ^3}\right) \right) . \end{aligned}$$
(3.1)

We need to find the expressions \(E(\ln (\frac{X-\mu }{\sigma }))\), \(E((\frac{X-\mu }{\sigma })^3)\) and \(E(\ln (1+e^{-(\frac{X-\mu }{\sigma })^3}))\). First, we calculate the expectation of \((\frac{X-\mu }{\sigma })^r\).

$$\begin{aligned} E\left( \left( \frac{X-\mu }{\sigma }\right) ^r\right) =\int _{-\infty }^{\infty }\frac{3p}{\sigma }\left( \frac{x-\mu }{\sigma }\right) ^{r+2}e^{-\left( \frac{x-\mu }{\sigma }\right) ^3}\left( 1+e^{-\left( \frac{x-\mu }{\sigma }\right) ^3}\right) ^{-p-1}\mathrm{d}x, \end{aligned}$$

using the change of variable, \(t=\frac{1}{1+e^{-(\frac{x-\mu }{\sigma })^3}}\), \(0<t<1\), and then, the change of variable, \(\frac{1}{t}-1=e^u\), \(0<u<\infty\), we obtain,

$$\begin{aligned} E\left( \left( \frac{X-\mu }{\sigma }\right) ^r\right) =(-1)^r p\sum _{i=0}^{\infty }{-p-1\atopwithdelims ()i}\frac{\Gamma \left( \frac{r}{3}+1\right) }{(p+i)^{\frac{r}{3}+1}}. \end{aligned}$$
(3.2)

For \(r=2k\)

$$\begin{aligned} E\left( \left( \frac{X-\mu }{\sigma }\right) ^{2k}\right) =p\sum _{i=0}^{\infty }{-p-1\atopwithdelims ()i}\frac{\Gamma \left( \frac{2k}{3}+1\right) }{(p+i)^{\frac{2k}{3}+1}}. \end{aligned}$$
(3.3)

Differentiating both sides of 3.3 with respect to k at \(k=0\) leads to

$$\begin{aligned} E\left( \ln \left( \frac{X-\mu }{\sigma }\right) \right) =\frac{p}{3}\sum _{i=0}^{\infty }{-p-1\atopwithdelims ()i}\frac{\Gamma ^{'}(1)-\ln (p+i)}{p+i}. \end{aligned}$$
(3.4)

In the same way, by calculating \(E((1+e^{-(\frac{X-\mu }{\sigma })^3})^r)\) and then differentiating with respect to r at \(r=0\), we obtain

$$\begin{aligned} E\left( \ln \left( 1+e^{-\left( \frac{X-\mu }{\sigma }\right) ^3}\right) \right) =\frac{1}{p}. \end{aligned}$$
(3.5)

By replacing 3.2, 3.4, and 3.5 in relation 3.1, the proof is completed. \(\square\)

Distribution of order statistics

The pdf of \(X_{i:n}\) \((i=1,\ldots ,n)\) is given by

$$\begin{aligned} f_{i:n}(x;\mu ,\sigma ,p)=\frac{n!}{(i-1)!(n-i)!}f(x;\mu ,\sigma ,p)F^{i-1} (x;\mu ,\sigma ,p)(1-F(x;\mu ,\sigma ,p))^{n-i}, \end{aligned}$$

where \(f(x;\mu ,\sigma ,p)\) and \(F(x;\mu ,\sigma ,p)\) are pdf and cdf given in 1.5 and 1.6, respectively:

$$\begin{aligned} f_{i:n}(x;\mu ,\sigma ,p)=\sum _{j=0}^{n-i}d_{j}(n,i)f(x;\mu ,\sigma , p(i+j)), \end{aligned}$$
(4.1)

where

$$\begin{aligned} d_{j}(n,i)=\frac{n!(-1)^j}{(i-1)!j!(n-i-j)!(i+j)}. \end{aligned}$$

Note that \(d_j(n,i) (j=0,1,\ldots ,n-i)\) are coefficients not dependent on p, \(\mu\), and \(\sigma\). This means that \(f_{i:n}(x;\mu ,\sigma ,p)\) is a weighted average of other new Burr.

From 1.6 and 4.1, we get the \(r^{\mathrm{th}}\) moment of \(X_{i:n}\) to be

$$\begin{aligned} E(X_{i:n}^r)= & {} \sum _{j=0}^{n-i}d_j(n,i)E(X^r) \\=\; & {} p\sum _{j=0}^{n-i}(i+j)d_j(n,i)\sum _{k=0}^{r}{r\atopwithdelims ()k}(-\sigma )^k \mu ^{r-k}E_q(g(Y)), \end{aligned}$$

where X has new Burr distribution with parameters \(\mu\), \(\sigma\) and \(p(i+j)\) and Y has q distribution, standard exponential distribution, and \(g(y)=(e^y+1)^{-p(i+j)-1}y^{\frac{k}{3}}e^{2y}\). Then, the importance sampling estimate of the \(r{\mathrm{th}}\) moment about origin of \(X_{i:n}\) is given by

$$\begin{aligned} p\sum _{j=0}^{n-i}(i+j)d_j(n,i)\sum _{k=0}^{r}{r\atopwithdelims ()k}(-\sigma )^k \mu ^{r-k}\left( \frac{1}{m}\sum _{l=1}^{m}g(Y_l)\right) ,Y_l\sim q. \end{aligned}$$
(4.2)

The cdf of \(X_{i:n}\) \((1\le i\le n)\) is given by

$$\begin{aligned} F_{i:n}(x)=I_{F(x)}(i,n-i+1), \end{aligned}$$

where \(I_x(a,b)\) is lower incomplete gamma function.

There, the \(100 u{\mathrm{th}}\) percentile of \(X_{i:n}\) can be obtained by solving

$$\begin{aligned} F_{i:n}(x)=u. \end{aligned}$$
(4.3)

The percentage points of \(X_{i:n}\) can be evaluated from 4.3 using tables of incomplete beta function (see [15]). However, for \(i=1\), Eq. 4.3 reduces to \((1-(1+e^{-(\frac{x-\mu }{\sigma })^3})^{-p})^n=1-u\). Thus, the 100u-percentage point of the smallest order statistic \(X_{1:n}\) is given by

$$\begin{aligned} F^{-1}_{1:n}(u;p,\mu ,\sigma )=\mu +\sigma \left( -\ln \left( \left( 1-(1-u)^{\frac{1}{n}}\right) ^{\frac{-1}{p}}-1\right) \right) ^{\frac{1}{3}}. \end{aligned}$$

Similarly, for \(i=n\), the 100u-percentage point of the largest order statistic is

$$\begin{aligned} F^{-1}_{n:n}(u;p,\mu ,\sigma )=\mu +\sigma \left( -\ln \left( u^{-\frac{1}{np}}-1\right) \right) ^{\frac{1}{3}}. \end{aligned}$$

Hazard change-point estimation-classical approach

Hazard function plays an important role in reliability and survival analysis. New Burr distribution has modified unimodal (unimodal followed by increasing) hazard function. In some medical situations, for example, breast cancer, the hazard rate of death of breast cancer patients represents a modified unimodal shape.

A modified unimodal shape has three phases: first increasing, then decreasing, and then again increasing. It can be interpreted as a description of three groups of patients, first group is represented by the first phase that contains the weak patients, so the hazard rate of this group is increasing, while the second phase represents the group with strong patients, their bodies have became familiar with the disease and they are getting better. The hazard rate of death of these patients is decreasing. In the third phase, they become weaker and their ability to cope with the disease declines, then the hazard rate of death increases.

For situations, where the hazard function is modified unimodal shaped, usually, we have interest in the estimation of lifetime change-point, that is , the point at which the hazard function reaches to a maximum (minimum) and then decreases (increase). In reliability, the change-point of a hazard function is useful in assessing the hazard in the useful life phase. One of change-points of hazard function of the new Burr distribution is location parameter. In this section, we consider maximum likelihood estimation procedure for change-points of the hazard function.

Let us assume that \(x_1,\ldots ,x_n\) is a random sample of size n of lifetimes generated by a new Burr distribution with parameters \(\mu\), \(\sigma\), and p. The log-likelihood function is given by

$$\begin{aligned} l(\mu ,\sigma ,p)=\; & {} n\log \left( \frac{3p}{\sigma }\right) +2\sum _{i=1}^{n}\log \left( \frac{x_i-\mu }{\sigma }\right) -\sum _{i=1}^{n}\left( \frac{x_i-\mu }{\sigma }\right) ^3-(p+1) \\&\sum _{i=1}^{n}\log \left( 1+e^{-\left( \frac{x_i-\mu }{\sigma }\right) ^3}\right) . \end{aligned}$$

The maximum likelihood estimates for \(\mu\), \(\sigma\), and p denoted by \(\hat{\mu }\), \(\hat{\sigma }\), and \(\hat{p}\), respectively, are obtained solving the likelihood equations, (\(\frac{\partial l}{\partial \mu }=0\), \(\frac{\partial l}{\partial \sigma }=0\), and \(\frac{\partial l}{\partial p}=0)\). According to the above, maximum likelihood estimator of one of change-points is \(\hat{\mu }\).

From the invariance property of maximum likelihood estimators, we can obtain maximum likelihood estimators for functions of \(\mu\), \(\sigma\) and p. For \(\phi =g(\mu ,\sigma ,p)\), a one-to-one function of \(\mu\), \(\sigma\), and p, and we have \(\hat{\phi }=g(\hat{\mu },\hat{\sigma },\hat{p})\). Taking \(\phi =h(x)\), defined in 1.7, the change-point of new Burr hazard function is obtained as solution of equation \(\frac{d}{\mathrm{d}x}\log (\phi )=0\). The maximum likelihood estimator of the change-point is the solution of \(\frac{d}{\mathrm{d}x}\log (\phi )=0\) with \(\mu\), \(\sigma\), and p replaced by maximum likelihood estimates. We observe that \(\frac{d}{\mathrm{d}x}\log (\phi )=0\) is non-linear in x, so the change-point of the hazard function estimate should be obtained using some one-dimensional root finding techniques, such as Newton–Raphson.

Testing new Burr model based on the Rényi Kullback–Leibler information

Test statistics

Suppose that we are interested in a goodness-of-fit test for

$$\begin{aligned} \left\{ \begin{array}{l} H_0:f(x)=f^0(x;\mu ,\sigma , p)=\frac{3p}{\sigma }\left( \frac{x-\mu }{\sigma }\right) ^2e^{-\left( \frac{x-\mu }{\sigma }\right) ^3}\left( 1+e^{-\left( \frac{x-\mu }{\sigma }\right) ^3}\right) ^{-p-1} \\ H_1:f(x)\ne f^0(x;\mu ,\sigma , p), \end{array} \right. \end{aligned}$$

where \(\mu\), \(\sigma\), and p are unknown.

We will denote the complete samples as \(X_{1:n}<X_{2:n}<\cdots <X_{n:n}\). For a null pdf \(f^0(x)\), the Rényi Kullback–Leibler information from complete data is defined as

$$\begin{aligned} D_r(f;f^0)=\frac{1}{r-1}\log \int _{-\infty }^{\infty }\cdots \int _{-\infty }^{x_{2:n}}\frac{(f_{X_{1:n},\ldots ,X_{n:n}}(x_{1:n},\ldots ,x_{n:n}))^{\alpha }}{(f^0_{X_{1:n},\ldots ,X_{n:n}}(x_{1:n},\ldots ,x_{n:n}))^{\alpha -1}}\mathrm{d}x_1\cdots \mathrm{d}x_n, \end{aligned}$$

where \(r>0\) and \(r\ne 1\). Because \(D_r(f;f^0)\) has the property that \(D_r(f;f^0)\ge 0\), and the equality holds if and only if \(f=f^0\), the estimate of the Rényi Kullback–Leibler information can be consider as a goodness-of-fit test statistic. For that purpose, the Rényi Kullback–Leibler information can be estimated by

$$\begin{aligned} D_r(f;f^0)=-H_r(X_{1:n},\ldots ,X_{n:n})-\sum _{j=1}^{n}f^0(x_j). \end{aligned}$$

Thus, the test statistics based on \(\frac{D_r(f;f^0)}{n}\) is given by

$$\begin{aligned} T_r=\frac{D_r(f;f^0)}{n}=\frac{1}{n}\left( -\hat{H}_r(X_{1:n},\ldots ,X_{n:n})-\sum _{j=1}^{n}f^0(x_j;\hat{\mu },\hat{\sigma },\hat{p})\right) , \end{aligned}$$

where \(\hat{\mu }\), \(\hat{\sigma }\), and \(\hat{p}\) are MLEs of \(\mu\), \(\sigma\), and p, respectively, and \(\hat{H}_r(X_{1:n},\ldots ,X_{n:n})\) is an estimate of Rényi entropy for sample \(X_{1:n}<X_{2:n}<\cdots <X_{n:n}\). Under the null hypothesis, \(T_r\) for r close to 1 will be close to 0, and therefore, large values of \(T_r\) will lead to the rejection of \(H_0\).

In this paper, we use estimation of Rényi entropy based on generalized nearest-neighbor graphs that is introduced by [14]. The basic tool to define their estimator was the generalized nearest-neighbor graph. This graph on vertex set V is a directed graph on V. The edge set of it contains for each \(i\in S\) (S is a finite non-empty set of positive integers), an edge from each \(x\in V\) to its i\(^{\mathrm{th}}\) nearest neighbor according to the Euclidean distance to x.

For \(p\ge 0\) denote by \(L_p(V)\), the sum of the p\(^{\mathrm{th}}\) powers of Euclidean lengths of its edges. According to proven theorem in [14]

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{L_p(X_{1:n},\ldots ,X_{n:n})}{n^{1-\frac{p}{d}}}=\gamma >0 \; a.s., \end{aligned}$$

where \(p=d(1-r)\) and d is dimension of sample members.

Based on described graph, they estimated Rényi entropy by

$$\begin{aligned} \hat{H}_r(X_{1:n},\ldots ,X_{n:n})=\frac{1}{1-r}\log \frac{L_p(X_{1:n},\ldots ,X_{n:n})}{\gamma n^{1-\frac{p}{d}}}. \end{aligned}$$

Application

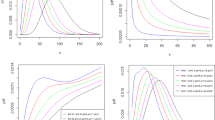
In this section, we consider an uncensored data set corresponding to remission times (in months) of a random sample of 128 bladder cancer patients. These data were previously reported in [10]. TTT plot for considered data is concave then convex indicating an increasing then decreasing hazard function, and is properly accommodated by new Burr distribution. Because in the system of Burr distributions, only Burr X and Burr XII distributions have unimodal hazard functions, and because of the similarity of cdf of the new Burr distribution with the Burr II distribution compared to the rest of distributions in Burr family, compare the fits of the new Burr distribution and those of Burr X, Burr XII, and Burr II and generalized Burr II. Plot of the estimated cdfs of models fitted to the data set is given in Fig. 3. Figure 3 and also values of defined test statistics in the previous section that are shown in Table 3 confirm that the new Burr distribution provides a significantly better fit than Burr X, Burr XII, Burr II, and generalized Burr II distributions. The required numerical evaluations are implemented using Matlab (version 2013) and R software (version 3.3.1).

Fig. 3
figure 3

cdfs of the new Burr, Burr X, Burr XII, Burr II, and generalized Burr II models for the remission times of bladder cancer data

Full size image
Table 3 Values of test statistics for the remission times of bladder cancer data
Full size table

Conclusions

We introduced a new family of Burr-type distributions as new Burr distribution. Various properties of the distribution are investigated. The distribution is found to be unimodal and bimodal. This new distribution with one parameter and simple form of cdf has modified unimodal (unimodal followed by increasing) hazard function. Hence, this new distribution can be used quite effectively in analyzing lifetime data with non-monotonic hazard function. The method of maximum likelihood is suggested for estimating the parameters and change-points of hazard function of the new Burr distribution. In application to remission times (in months) of a random sample of 128 bladder cancer patients, the new Burr distribution provided a significantly better fit than Burr X, Burr XII, Burr II, and generalized Burr II distributions. This fact is confirmed by goodness-of-fit test statistic based on the Rényi Kullback–Leibler information.