Skip to main content
SpringerLink
Log in

Design Curves for Estimation of Amplification Factor in the Slope Topography Considering Nonlinear Behavior of Soil

  • Original Paper
  • Published:
Indian Geotechnical Journal Aims and scope Submit manuscript

Abstract

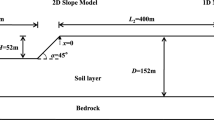
Both surface and in-depth topography have significant effects on the earthquake records and inflicted damages. Despite various studies, the effects of topography have not yet been addressed comprehensively by the current construction codes. The effect of slope topography was investigated in this study considering the real (elastoplastic) behavior of the materials and the effects of the increase in stiffness with the depth on the ground surface response using numerical analysis. Such parameters as input motion frequency, slope height and angle, and the material type were evaluated. The finite-element software tool MIDAS GTS NX was used for modeling. The study results were presented as the acceleration amplification factor, which is the ratio of the maximum two-dimensional ground acceleration to the maximum one-dimensional ground acceleration. The results showed that the seismic analysis of slope topography had a significant effect on the surface amplification factor near the crest and toe of the slope. According to the evaluated parameters, the areas affected by topography on the ground types dense and medium dense reach the x/H = 1.5 and x/H = 0.67 of the crest, respectively. In this condition, the amplification factor of acceleration for the ground types dense and medium dense will be in 1–3.5 and 1.5–3 ranges, respectively.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20

Similar content being viewed by others

Abbreviations

f :

Dominant frequency

G o :

Initial shear modulus

γ 0.7 :

Threshold shear strain

ξ :

Damping ratio

E D :

Dissipated energy

E S :

Maximum strain energy

\(G_{0}^{\text{ref}}\) :

Reference initial shear modulus at the reference pressure (pref) of 100 kPa

c′ and φ′ :

Soil strength parameters

\(\sigma_{3}^{'}\) :

Minimum principal effective stress

\(E_{\text{ur}}^{\text{ref}}\) :

Loading–unloading stiffness

\(E_{50}^{\text{ref}}\) :

Secant stiffness in the drained triaxial test

\(E_{\text{oed}}^{\text{ref}}\) :

Tangent stiffness for the initial oedometer loading

V s :

Shear wave velocity

[C], [M], and [K]:

Matrices of damping, mass, and stiffness

αR and βR :

Coefficients proportional to mass and stiffness

ωi and ωj :

Natural frequencies of two vibration modes

References

  1. Zhang N, Gao Y, Dai D (2017) Ground motion at a semi-cylindrical valley partially filled with a crescent shaped soil layer under incident plane SH waves. J Earthq Tsunami 11(03):1750007

    Article  Google Scholar 

  2. Tripe R, Kontoe S, Wong TKC (2013) Slope topography effects on ground motion in the presence of deep soil layers. Soil Dyn Earthq Eng 50:72–84

    Article  Google Scholar 

  3. Assimaki D, Kausel E (2007) Modified topographic amplification factors for a single-faced slope due to kinematic soil-structure interaction. J Geotech Geoenviron Eng 133(11):1414–1431

    Article  Google Scholar 

  4. Pedersen H, Le Brun B, Hatzfeld D, Campillo M, Bard PY (1994) Ground-motion amplitude across ridges. Bull Seismol Soc Am 84(6):1786–1800

    Google Scholar 

  5. Geli L, Bard PY, Jullien B (1988) The effect of topography on earthquake ground motion: a review and new results. Bull Seismol Soc Am 78(1):42–63

    Google Scholar 

  6. Bouckovalas GD, Papadimitriou AG (2005) Numerical evaluation of slope topography effects on seismic ground motion. Soil Dyn Earthq Eng 25(7–10):547–558

    Article  Google Scholar 

  7. Zhang Z, Fleurisson JA, Pellet F (2018) The effects of slope topography on acceleration amplification and interaction between slope topography and seismic input motion. Soil Dyn Earthq Eng 113:420–431

    Article  Google Scholar 

  8. Gazetas G, Kallou PV, Psarropoulos PN (2002) Topography and soil effects in the Ms 5.9 Parnitha (Athens) earthquake: the case of adames. Nat Hazards 27(1–2):133–169

    Article  Google Scholar 

  9. Rizzitano S, Cascone E, Biondi G (2014) Coupling of topographic and stratigraphic effects on seismic response of slopes through 2D linear and equivalent linear analyses. Soil Dyn Earthq Eng 67:66–84

    Article  Google Scholar 

  10. Bararpour M, Janalizade A, Tavakoli HR (2016) The effect of 2D slope and valley on seismic site response. Arabian J Geosci 9(2):93

    Article  Google Scholar 

  11. Tsai CC, Lin CH (2018) Prediction of earthquake-induced slope displacements considering 2D topographic amplification and flexible sliding mass. Soil Dyn Earthq Eng 113:25–34

    Article  Google Scholar 

  12. Dhakal S (2004) Empirical relations for earthquake response of slopes. MSc thesis, International Institute for Geo-information Science and Earthquake observation, Netherlands

  13. Soltani N, Bagheripour MH (2017) Seismic wave scatter study in valleys using coupled 2D finite element approach and absorbing boundaries. Sci Iran 24(1):110–120

    Google Scholar 

  14. Narayan JP, Kumar A (2018) Quantification of effects of ridge and valley topography on the Rayleigh wave characteristics. J Earthq Tsunami 12(03):1850007

    Article  Google Scholar 

  15. Poursartip B, Kallivokas LF (2018) Model dimensionality effects on the amplification of seismic waves. Soil Dyn Earthq Eng 113:572–592

    Article  Google Scholar 

  16. Glinsky N, Bertrand E, Régnier J (2019) Numerical simulation of topographical and geological site effects. Applications to canonical topographies and rognes hill, South East France. Soil Dyn Earthq Eng 116:620–636

    Article  Google Scholar 

  17. Song KI, Oh TM, Cho GC (2014) Precutting of tunnel perimeter for reducing blasting-induced vibration and damaged zone-numerical analysis. KSCE J Civil Eng 18(4):1165–1175

    Article  Google Scholar 

  18. Gao X, Zhang D, Absai V, Feng H, Yi J (2016) Computational simulation of coupled geodynamics for forming the makeng deposit in fujian province, China: constraints of mechanics, thermotics and hydrology. J Geochem Explor 160:31–43

    Article  Google Scholar 

  19. Niu J, Jiang X, Wang F (2018) Stability analysis of rock slope with small spacing tunnel under earthquakes and influence of ground motion parameters. Geotech Geol Eng 36(4):2437–2453

    Article  Google Scholar 

  20. Shamsi M, Ghanbari A (2019) Nonlinear dynamic analysis of Qom Monorail Bridge considering Soil-Pile-Bridge-Train Interaction. Transport Geotech. https://doi.org/10.1016/j.trgeo.2019.100309

    Article  Google Scholar 

  21. Sitar N, Clough GW (1983) Seismic response of steep slopes in cemented soils. J Geotech Eng 109(2):210–227

    Article  Google Scholar 

  22. Assimaki D, Kausel E, Gazetas G (2005) Soil-dependent topographic effects: a case study from the 1999 Athens earthquake. Earthq Spect 21(4):929–966

    Article  Google Scholar 

  23. Pain A, Annapareddy VSR, Sarkar S (2019) Seismic stability analysis of municipal solid waste landfills using strain dependent dynamic properties. Indian Geotech J 49:204. https://doi.org/10.1007/s40098-018-0314-6

    Article  Google Scholar 

  24. Paolucci R (2002) Amplification of earthquake ground motion by steep topographic irregularities. Earthq Eng Struct Dyn 31(10):1831–1853

    Article  Google Scholar 

  25. Bi K, Hao H (2011) Influence of irregular topography and random soil properties on coherency loss of spatial Seismic ground motions. Earthq Eng Struct Dyn 40(9):1045–1061

    Article  Google Scholar 

  26. Luo C, Lou M, Gui G, Wang H (2019) A modified domain reduction method for numerical simulation of wave propagation in localized regions. Earthq Eng Eng Vib 18(1):35–52

    Article  Google Scholar 

  27. Khanbabazadeh H, Iyisan R (2014) A numerical study on the 2D behavior of the single and layered clayey basins. Bull Earthq Eng 12(4):1515–1536

    Article  Google Scholar 

  28. Jeong S, Asimaki D, Dafni J, Wartman J (2019) How topography-dependent are topographic effects? Complementary numerical modeling of centrifuge experiments. Soil Dyn Earthq Eng 116:654–667

    Article  Google Scholar 

  29. Amorosi A, Boldini D, Elia G (2010) Parametric study on seismic ground response by finite element modelling. Comput Geotech 37(4):515–528

    Article  Google Scholar 

  30. Fargnoli V, Gragnano CG, Boldini D, Amorosi A (2015) 3D numerical modelling of soil–structure interaction during EPB tunnelling. Géotech 65(1):23–37

    Article  Google Scholar 

  31. Hardin BO, Drnevich VP (1972) Shear modulus and damping in soils: measurement and parameter effects. J Soil Mech Found Div 98(6):603–624

    Google Scholar 

  32. Seed HB, Wong RT, Idriss IM, Tokimatsu K (1986) Moduli and damping factors for dynamic analyses of cohesionless soils. J Geotech Eng 112(11):1016–1032

    Article  Google Scholar 

  33. Sun JI, Golesorkhi R, Seed HB (1988) Dynamic moduli and damping ratios for cohesive soils. Earthquake Engineering Research Center, University of California, Berkeley

    Google Scholar 

  34. Bajaj K, Anbazhagan P (2019) Identification of shear modulus reduction and damping curve for deep and shallow sites: Kik-Net data. J Earthq Eng. https://doi.org/10.1080/13632469.2019.1643807

    Article  Google Scholar 

  35. Brinkgreve RBJ, Kappert MH, Bonnier PG (2007) Hysteretic damping in a small-strain stiffness model. In: Proceedings of the 10th international symposium on numerical models in geomechanics (NUMOG 10), pp 737–742

  36. FEMA 450 (2003) NEHRP recommended provisions for seismic regulation for new buildings and other structures. Building Seismic Safety Council of the National Institute of Building Sciences, Washington, D.C.

    Google Scholar 

  37. Ghanbari E, Hamidi A (2015) Improvement parameters in dynamic compaction adjacent to the slopes. J Rock Mech Geotech Eng 7(2):233–236

    Article  Google Scholar 

  38. Amorosi A, Boldini D, Di Lernia A (2016) Seismic ground response at Lotung: hysteretic elasto-plastic-based 3D analyses. Soil Dyn Earthq Eng 85:44–61

    Article  Google Scholar 

  39. Di Fiore V (2010) Seismic site amplification induced by topographic irregularity: results of a numerical analysis on 2D synthetic models. Eng Geol 114(3–4):109–115

    Article  Google Scholar 

  40. Dafni J (2017) Experimental investigation of the topographic modification of earthquake ground. Ph.D. thesis, University of Washington

  41. Tarazona SFM, Almeida MCFD, Bretschneider A, Almeida MDSSD, Escoffier S, Borges RG (2019) Evaluation of seismic site response of submarine clay canyons using centrifuge modelling. Int J Phys Model Geotech. https://doi.org/10.1680/jphmg.18.00084

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Civil Engineering, Kharazmi University, Mofatteh Avenue, P.O. Box 15719-14911, Tehran, Iran

    Mohammad Javad Shabani & Ali Ghanbari

Authors
  1. Mohammad Javad Shabani
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ali Ghanbari
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mohammad Javad Shabani.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shabani, M.J., Ghanbari, A. Design Curves for Estimation of Amplification Factor in the Slope Topography Considering Nonlinear Behavior of Soil. Indian Geotech J 50, 907–924 (2020). https://doi.org/10.1007/s40098-020-00443-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40098-020-00443-1

Keywords

Search

Navigation