1 Introduction

Arc welding is a process of melting and joining workpiece using arc plasma heat generated by electric discharge. The arc is composed of ionized gas, which is electrically neutral at high current resulting in high temperatures and strong process light during the process. Consequently, analytical and numerical studies have been actively underway in terms of the welding design, in which modeling of the arc heat source is performed to calculate the residual stress and thermal deformation, and the results are utilized to design the welding structure [1]. In the 1940s, Rosenthal first calculated the shape of molten pool in arc welding by using a moving point heat source [2]. The point heat source was applied on the undeformed surface of the workpiece, and only thermal conduction was considered. This approach can be used to predict the temperatures far enough from the arc because the error increases near the arc. To date, the arc assumes as a Gaussian heat source, and welding-specialized software based on the finite element method (FEM) has been commercialized with improved accuracy. Even the residual stress and the deformation considering the phase transformation can be easily calculated [3]. However, the FEM analysis based on the thermal conduction model has a limitation that it cannot directly consider the effect of the molten pool flow.

Therefore, numerical studies to analyze the molten pool flow have been conducted by computational fluid dynamics (CFD). In the early stages, the simulations were performed without considering the molten pool deformation. For this reason, gas tungsten arc (GTA) welding at low current is mainly considered thanks to its small deformation. Kim et al. (1989) analyzed the axisymmetric molten pool in static GTA welding. The driving forces—electromagnetic force, buoyancy, surface tension, and drag by gas—were considered, and the molten pool surface was assumed flat [4]. A numerical study considering the deformed molten pool surface was also conducted [5]. In gas metal arc (GMA) welding, a three-dimensional quasi-steady-state heat transfer and molten pool flow analysis considering the deformation of the molten pool surface was performed using a boundary-fitted coordinate system, in which electromagnetic force, buoyancy, and surface tension were considered. The results showed that a long molten pool was created behind the arc, and buoyancy and surface tension had a minor effect on the molten pool shape. A finger-shaped penetration was observed only when the molten pool convection was considered in simulation [6]. In a follow-up research, molten droplets were imposed on the molten pool surface as a velocity distribution with the Gaussian function, and the effect of the contact tip to workpiece distance (CTWD) was examined. It was found that their effects on the molten pool were significant [7]. Lee et al. (1995) performed a numerical study of the arc behavior in GTA welding using the boundary-fitted coordinate system. The actual electrode shape was considered assuming that the current density had the Gaussian distribution. It was possible to predict not only the temperature distribution of the arc but also the current density, heat flow, arc pressure, and drag transmitted [8]. In a further study, effects of the electrode angle and arc length were examined. The results showed that the electrode angle did not significantly affect the heat flow and current density distribution, but it had a great effect on arc pressure and drag compared to the arc length. In particular, the change of the arc pressure was negligible even when the arc length was changed [9]. In the follow-up study, the change of molten pool surface was considered in the arc analysis [10]. An integrated modeling of arc and molten pool behavior was performed as well [11]. In the abovementioned studies, the shape of the molten pool surface was obtained through iterative calculation minimizing the surface total energy. However, the method is not suitable for analyzing cases with a large molten pool deformation like a molten droplet transfer. As an indirect method to consider the droplet transfer, the method of adding the momentum and enthalpy of the droplet [12], the coordinate transformation method [13], and the method of adding the volumetric heat source of the droplet [14] were used. Free surface tracking algorithms (e.g., the volume-of-fluid (VOF) method) allow direct consideration of molten pools with large surface deformations. Choi et al. (1998) predicted the free surface, velocity, and pressure change in the short-run mode GMA welding using the VOF method [15]. Ko et al. (2000) analyzed the effects of molten pool surface change on flow and vibration in stationary GTA welding using the VOF method [16]. In recent years, a three-dimensional transient molten pool analysis of arc welding has been performed in that the computation time is greatly reduced even in a bigger computational domain thanks to the advancement of computing technology and algorithms. A three-dimensional transient molten pool analysis considering the droplet transfer was performed for the fillet joint [17], and an integrated analysis of the arc and the molten pool was also conducted [18]. Pulsed GMA weaving welding analysis was performed for V-groove-shaped welds using the results of dynamic arc behavior analysis based on simplified RL circuit of the welding power supply. The arc heat source distribution obtained by the Abel inversion of the arc shapes observed by a CCD camera was used in simulation [19]. Molten pool behavior in the gas hollow tungsten arc (GHTA) spot welding process was also calculated at a low-pressure-gravity state like in space [20]. Kiran et al. (2015) conducted a three-dimensional simulation to understand the temperature distribution and molten pool behavior in a three-submerged-arc welding process. They showed that weld width was significantly influenced by the leading arc and the penetration by the middle and trailing arcs [21].

In this study, mathematical models presented in the literature were used for GMA welding simulation. In order to examine the effect of the driving force on the molten pool, a 2D axisymmetric simulation was conducted in stationary arc welding, and the maximum velocity components were compared in terms of the driving forces. In the 3D transient analysis, additional conservation equations for the alloying elements were used to calculate the distribution of the alloying elements supplied by the consumable electrode. The models used were verified by comparing the fusion zone shape and the alloy element distribution measured in the experiment.

2 Methodology

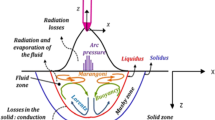
To analyze the effects of the driving forces (buoyancy, drag, arc pressure, electromagnetic force, Marangoni force, and droplet impingement), the molten pool behavior was calculated in stationary arc welding. Figure 1 shows the 2D axisymmetric computational domain and cylindrical mesh used in the simulation. Table 1 shows the boundary conditions for the computational domain. Table 2 shows the simulation cases for the six driving forces, and for the Marangoni force, and three cases with sulfur contents of 0 ppm, 130 ppm, and 500 ppm were considered. ASTM A36 steel was used in this study, and the reason for selecting the different sulfur contents is as follows: 500 ppm is the maximum sulfur content of ASTM A36 steel published in the industry standard. And 130 ppm is the sulfur content measured in the literature [22]. Figure 2 shows the change in surface tension with temperature for the three sulfur contents [23]. A three-dimensional transient analysis of GMA welding was also performed to verify the models used. Figure 3 shows the 3D computational domain and the Cartesian mesh used in the simulation. The computational domain near the area where the melting occurred was divided into a minimum mesh size of 0.2 mm as recommended in the literature [24]. Table 3 shows the boundary conditions of the 3D domain, which were defined so that the differential values of all independent variables are 0 (Neumann boundary condition).

Fig. 1
figure 1

a, b Schematic diagram of solution domain and mesh for axisymmetric stationary arc welding simulation

Full size image
Table 1 Boundary conditions for two-dimensional axisymmetric stationary arc welding simulation
Full size table
Table 2 Simulation cases for stationary arc welding
Full size table
Fig. 2
figure 2

Surface tension vs. temperature for an Fe-S system containing different amounts of sulfur [23]

Full size image
Fig. 3
figure 3

a, b Schematic diagram of solution domain and mesh for three-dimensional moving arc welding simulation

Full size image
Table 3 Boundary conditions for three-dimensional moving arc welding simulation
Full size table

The workpiece was a 10-mm-thick structural carbon steel (ASTM A36). The thermophysical properties used in the simulation are shown in Table 4. For the consumable electrode, a stainless steel solid wire (Y308) was used. The reason for using the stainless solid wire is that it is expected to be easy to experimentally analyze the alloying element distribution because the workpiece (A36 steel) has no chromium and nickel contents, whereas the wire (Y308) has high chromium and nickel contents with 20% and 10%, respectively. Welding conditions used in the simulation were the same as those in the experiment: an arc voltage of 28 V, an arc current of 231 A, a wire feeding rate of 8 m/min, a welding speed of 1 m/min, and a torch angle of 61°.

Table 4 Thermophysical material properties of materials used in simulation
Full size table

2.1 Governing equations

In this study, the basic governing equations—mass conservation, momentum conservation, and energy conservation equation—are used to perform a three-dimensional transient analysis of the heat and mass flow during the arc welding process. In addition, the VOF equation for tracking free surface and additional conservation equations for calculating the alloying element distribution were introduced. Assuming Newtonian fluid and incompressible laminar flow, the governing equations used in this study are as follows.

Mass conservation equation:

$$ \nabla \cdotp v=\frac{{\dot{m}}_s}{\rho } $$
(1)

where, v is the velocity, \( {\dot{m}}_s \) is a mass source by molten droplets, and ρ is the density.

Momentum conservation equation:

$$ \frac{\partial v}{\partial t}+v\cdotp \nabla v=-\frac{1}{\rho}\nabla p+\nu {\nabla}^2v- Kv+\frac{{\dot{m}}_s}{\rho}\left({v}_s-v\right)+G $$
(2)

where, \( K=C\frac{{F_s}^2}{{\left(1-{F}_s\right)}^3+B} \),

where, p is the pressure, ν is the dynamic viscosity, K is the drag coefficient for the porous media model in the mushy zone, vs is the velocity vector for the mass source, G is the body acceleration by body forces, C is a constant for mushy zone morphology, Fs is the solid fraction, and B is a positive zero to prevent being divided by 0. The third term on the right side of Eq. (2) represents the amount of momentum dissipated by friction in the mushy zone. The mushy zone is a region where the temperature is between the solidus and the liquidus. In this area, the dynamic viscosity and the drag coefficient were calculated using the lever rule. As shown in Fig. 4, the mushy zone is further divided into three regions by the coherent solid fraction (0.15) and the critical solid fraction, Fcr (0.67). If the solid fraction is larger than the critical solid fraction, the dynamic viscosity and the drag coefficient are large enough to indicate that there is no fluid flow. If the solid fraction is smaller than the critical solid fraction, the dynamic viscosity is calculated by using the equation \( \nu ={\nu}_0{\left(1-\frac{F_s}{F_{cr}}\right)}^{-1.55} \). The drag coefficient is 0 in the region where the solid fraction is smaller than the coherent solid fraction because the solid crystals, which are sparsely distributed, do not form a coherent solid structure but float freely in the liquid. In the area where the solid fraction is between the coherent solid fraction and the critical solid fraction, the equation presented in (2) is used, which is obtained through the Carman-Kozeny equation derived from the Darcy model by assuming that the mushy zone can be regarded as a porous medium [26].

Fig. 4
figure 4

Dynamic viscosity and drag coefficient in the mushy zone

Full size image

Energy conservation equation:

$$ \frac{\partial h}{\partial t}+v\cdotp \nabla h=\frac{1}{\rho}\nabla \cdotp \left(k\nabla T\right)+{\dot{h}}_s $$
(3)

where, h is the enthalpy, k is the thermal conductivity, T is the temperature, and \( \dot{h_s} \) is the enthalpy source term by the mass source. The enthalpy-based continuum model in Eq. (4) was used to consider the phase change between solid and liquid.

$$ h=\left\{\begin{array}{c}{\rho}_s{C}_sT\\ {}h\left({T}_s\right)+{h}_{sl}\frac{T-{T}_s}{T_l-{T}_s}\\ {}h\left({T}_l\right)+{\rho}_l{C}_l\left(T-{T}_l\right)\end{array}\kern0.5em \begin{array}{c}\left(T\le {T}_s\right)\\ {}{T}_s\le T\le {T}_l\\ {}\left({T}_l\le T\right)\end{array}\right. $$
(4)

where, ρs and ρl are the solid and liquid density, Cs and Cl are the solid and liquid specific heat, and Ts and Tl are the solidus and liquidus temperature, respectively. hsl is the latent heat of fusion.

VOF equation:

$$ \frac{\partial F}{\partial t}+\nabla \cdotp (vF)={\dot{F}}_s $$
(5)

where, F is the volume of fluid and \( {\dot{F}}_s \) is the volume source by the mass source.

Additional conservation equation:

In order to simulate the distribution and behavior of alloying elements over time, the following additional conservation equation was used, which is the common advection equation like the VOF equation.

$$ \frac{\partial \varPhi }{\partial t}+\nabla \cdotp \left( v\varPhi \right)={\dot{\varPhi}}_s $$
(6)

where, Φ is the volume fraction of alloying element and \( {\dot{\varPhi}}_s \) is the source term by the mass source. Here, diffusion effect of the alloying elements was not considered.

2.2 Boundary conditions

Energy input due to arc heat flux and energy losses due to convection, radiation, and evaporation imposed on the workpiece. These can be expressed as follows.

$$ q\left(x,y,z\right)={q}_A-{q}_{\mathrm{conv}}-{q}_{\mathrm{rad}}-{q}_{\mathrm{evap}}={q}_A-h\left(T-{T}_0\right)-{\varepsilon}_r\sigma \left({T}^4-{T_0}^4\right)-{q}_{\mathrm{evap}} $$
(7)

where, qA is the arc heat flux, qconv is the convective heat loss, qrad is the radiative heat loss, qevap is the heat loss by evaporation, h is the convective heat transfer coefficient, T0 is the ambient temperature, εr is the surface radiation emissivity, and σ is the Stefan-Boltzmann constant. It was assumed that 18% of the evaporated material were re-condensed on the surface. The heat fluxes defined in Eq. (7) were applied to the free surface cells using the source term in Eq. (3). On the bottom surface, only convection and radiative heat losses were considered.

The pressure boundary condition on the free surface can be expressed by the pressure balance of arc pressure and surface tension as follows.

$$ p={p}_A+\frac{\gamma }{R_c} $$
(8)

where, pA is the arc pressure, γ is the surface tension, and Rc is the surface curvature.

2.3 Mathematical models for arc welding

2.3.1 Arc heat source and droplet generation

In this study, the arc heat source was modeled with the Gaussian surface heat flux.

$$ {\eta}_A{q}_A\left(x,y\right)={\eta}_A\frac{VI}{2\uppi {r_A}^2}\exp \left(-\frac{x^2+{y}^2}{2{r_A}^2}\right) $$
(9)

where, ηA is the arc efficiency, V is the arc voltage, I is the arc current, and rA is the effective radius of the arc heat source. In GMA welding, the overall efficiency is expressed as the sum of the arc efficiency and the droplet generation efficiency. In this study, droplets were generated at the frequency, fd, which can be calculated using Eq. (10). The droplet temperature was 2400 K, and the droplet radius, rd, was equal to the electrode radius, rw.

$$ {f}_d=\frac{5{r_w}^2\mathrm{WFR}}{4{r_d}^3}\left(\mathrm{Hz}\right) $$
(10)

where, WFR is the wire feeding rate.

The droplet generation efficiency can be calculated as follows.

$$ {\eta}_d=\frac{4}{3 VI}\uppi {r_d}^3\rho \left[{C}_s\left({T}_s-{T}_0\right)+{C}_l\left({T}_d-{T}_s\right)+{h}_{sl}\right]{f}_d $$
(11)

Therefore, assuming that the overall efficiency of the GMA welding is 80%, the arc efficiency can be calculated as follows.

$$ {\eta}_A=0.8-{\eta}_d $$
(12)

2.3.2 Arc pressure, Marangoni force, and drag force

Of the driving forces generated in arc welding, the surface forces include arc pressure, Marangoni force, and drag force. The arc pressure was applied by using the following Gaussian function [27].

$$ {P}_A\left(x,y\right)=\frac{F}{2\uppi {r_A}^2}\exp \left(-\frac{x^2+{y}^2}{2{r_A}^2}\right) $$
(13)

where, F is the total arc force.

The molten pool surface is subjected to shear force by the temperature and the surface active element, causing a flow called the Marangoni flow. The following equation was used to account for the change in surface tension according to the temperature and the active element [28].

$$ \gamma (T)={\gamma}_m^o-A\left(T-{T}_m\right)-\bar{R}T{\varGamma}_s\mathit{\ln}\left(1+{k}_1{a}_i{e}^{-\varDelta {H}^o/\bar{R}T}\right) $$
(14)

where, \( {\gamma}_m^o \) is the surface tension of pure metal at the melting temperature, A is the surface tension gradient of pure metal, Tm is the melting temperature, Γs is the surface excess at saturation, k1 is the constant related to the entropy of segregation, ai is the thermodynamic activity of component, and ΔHo is the standard heat of adsorption.

The drag force is generated by the arc plasma jet colliding with the molten pool surface and spreading from the center. The following analytical solution for the shear stress that occurs when the jet impinges perpendicular to a flat surface was used in simulation [29].

$$ \frac{\tau }{\rho_p{u}_0^2}{\mathit{\operatorname{Re}}}_0^{1/2}{\left(\frac{H}{D}\right)}^2={g}_2\left(\frac{r}{H}\right) $$
(15)

where, τ is the shear stress, ρp is the plasma density, u0 is the initial velocity, Re0 is the Reynolds number, H is the nozzle height, D is the nozzle diameter, r is the radius, and g2 is the universal function. For the arc plasma jet, H and D were assumed to be the arc length and the electrode diameter, respectively.

2.3.3 Electromagnetic force and buoyancy force

Of the driving forces generated in arc welding, the body forces include electromagnetic force and buoyancy force.

The radial and vertical components of electromagnetic force were calculated using the analytical solution by Kou and Sun as follows [30].

$$ {F}_r=-{J}_z{B}_{\theta } $$
(16)
$$ {F}_z={J}_r{B}_{\theta } $$
(17)

where,

$$ {J}_z=\frac{I}{2\uppi}{\int}_0^{\infty}\lambda {J}_0\left(\lambda r\right)\exp \left(-{\lambda}^2{r_A}^2/12\right)\frac{\sin h\left[\lambda \left(c-z\right)\right]}{\sin h\left(\lambda c\right)} d\lambda $$
$$ {J}_r=\frac{I}{2\uppi}{\int}_0^{\infty}\lambda {J}_1\left(\lambda r\right)\exp \left(-{\lambda}^2{r_A}^2/12\right)\frac{\cos h\left[\lambda \left(c-z\right)\right]}{\sin h\left(\lambda c\right)} d\lambda $$
$$ {B}_{\theta }=\frac{\mu_mI}{2\uppi}{\int}_0^{\infty }{J}_1\left(\lambda r\right)\exp \left(-{\lambda}^2{r_A}^2/12\right)\frac{\sin h\left[\lambda \left(c-z\right)\right]}{\sin h\left(\lambda c\right)} d\lambda $$

where, Jz and Jr are the vertical and radial components of the current density, respectively. Bθ is the angular magnetic field. J0 and J1 are the first kinds of Bessel function of zero order and the first order, respectively. c is the thickness of the workpiece, z is the vertical distance, and μm is the magnetic permeability.

Buoyancy is caused by a change in the density of the molten pool. Since it is difficult to know the density change of steel at temperature above the melting point, the coefficient of thermal expansion was used to indirectly account for the density change due to the temperature difference by the Boussinesq approximation.

$$ {F}_b=\rho \kern0em g\beta \left(T-{T}_0\right) $$
(18)

where, β is the coefficient of thermal expansion.

3 Results and discussion

Figure 5 shows the simulation results for the cases in Table 2. As shown in Fig. 5a, the case with no driving force formed a semi-circular molten pool with a negligible flow. Figure 5b shows the simulation result considering only buoyancy. The clockwise-rotating pattern was observed in the molten pool, but the molten pool shape was similar to the shape in Fig. 5a because the flow was also quite small. Figure 5c shows the result for the case considering only the drag generated by the arc plasma jet colliding with the molten pool surface, in which a flow pattern spreading in the radial direction was observed. This flow was large enough to change the molten pool shape, resulting in a wider, shallower molten pool compared to the shapes in Fig. 5a and b. Figure 5d shows the simulation result considering only the arc pressure. Due to a strong downward flow generated, a deep molten pool was formed. As shown in Fig. 5e, the case considering only the electromagnetic force also showed a deep penetration together with a similar flow pattern rotating in a counterclockwise direction. Figure 5f–h shows the simulation results considering only the Marangoni force for the cases with sulfur contents of 0 ppm, 130 ppm, and 500 ppm. As shown in Fig. 2, as the sulfur content increases, the surface tension decreases, and the region with a positive surface tension gradient increases. The negative surface tension gradient causes surface flows from the center to the outside, resulting in a wide, shallow molten pool, whereas the positive gradient forms a narrow, deep molten pool by generating surface flows from the outside to the center. The simulation results also showed that as the sulfur content increased, the width of the molten pool decreased, and the depth increased. Figure 5i shows the simulation result considering only the droplet impingement. The droplet was spherical with the same radius as that of the solid wire, and the droplet generation frequency was calculated using the wire feeding speed as shown in Eq. (10). The droplet temperature was 2400 K and the speed was 35 cm/s in the -z-direction. Due to the large downward flow by the impingement, the molten pool was deepest among the simulation cases. Figure 5j shows the simulation result considering all the driving forces mentioned. What is unique about this case compared to the result in Fig. 5i is that the depth is shallower, and the width is wider due to the interaction of the driving forces. Of the driving forces, buoyancy, drag, and Marangoni forces tended to create a wide and shallow molten pool, whereas electromagnetic force, arc pressure, and droplet impingement created a deep molten pool. Figure 6 shows the average values of the maximum velocities in the molten pool of each case measured from 2 to 4 s with a period of 0.01 s.

Fig. 5
figure 5figure 5

a–j Temperature profile and molten pool flow in stationary arc spot welding simulation

Full size image
Fig. 6
figure 6

Average of maximum velocities with respect to driving force (2–4s)

Full size image

For the radial velocity component, the results are as follows:

  • Buoyancy ≪ arc pressure < EMF < drag < Marangoni < droplet.

For the vertical velocity component, the results are as follows:

  • Buoyancy ≪ drag < arc pressure < EMF < Marangoni ≪ droplet.

From the above results, the buoyancy is negligible compared to other driving forces, so it is not necessary to consider it in the simulation of GMA welding. On the other hand, the droplet impingement is the most important driving force that determines maximum velocity values not only in radial but also in axial direction. Especially it is the dominant factor that determines penetration depth. The next most effective driving force is the Marangoni force, which increases the molten pool width in the sulfur content range considered in this study. Therefore, the interaction between the droplet impingement and the Marangoni force makes the penetration depth in Fig. 5j smaller compared to Fig. 5i.

Figure 7 shows the temperature distribution of 3D transient simulation of GMA welding considering all the driving forces mentioned. In the side view, the droplet was generated and transferred according to the set conditions. The droplet collided made a concave molten pool surface in which the molten pool was deepest. Therefore, it is thought that the droplet impingement is dominant to determine the molten pool depth in moving arc welding. Since the downward flow was blocked at the solid-liquid interface, the flow rolled up in the opposite of the welding direction. Due to this flow, the molten pool with the high temperature generated by the droplet and arc flux was pushed backward, and thus the cooling at the molten pool tail was slow, forming an elongated molten pool. In the front view, cooling occurred from the bottom up, and the flow was directed from top to bottom at the molten pool near the droplet impingement, but afterwards the flow mainly occurred from bottom to top. In Fig. 8, the shapes of the fusion zone obtained from the simulation and the experiment were compared. In the simulation, the bead height was 0.23 cm, the width was 0.66 cm, and the penetration depth was 0.13 cm. In the experiment, the height was 0.23 cm, the width was 0.62 cm, and the depth was 0.16 cm. It showed that the mathematical models used in this study were appropriate for simulating the GMA welding.

Fig. 7
figure 7

a–d Simulation results of temperature views over time in GMA welding

Full size image
Fig. 8
figure 8

Comparison of the numerical and experimental fusion zone shape in GMA welding

Full size image

As shown in Fig. 9, the behavior and distribution of chromium in the molten pool were calculated using the additional conservation equation described in Eq. (6). The distribution of nickel was the same as that of chromium, except that the value was only a half. This was because the diffusion effect was not considered, and both chromium and nickel were determined by the same molten pool flow. Similar results were also seen in the experimental results in Fig. 10. The boundary shape of the fusion zone and the chromium and nickel distribution were the same, and the chromium and nickel distributions had different absolute values, but they had a similar distribution pattern. The results show that when calculating the behavior and distribution of chromium and nickel, only the flow can be considered ignoring the diffusion effect as in Eq. (6). In addition, it was found that the alloy element distribution was higher at the bottom, which is considered to be because the alloy elements supplied by droplets reached the bottom due to the high vertical velocity, but they were partially trapped at the solid-liquid interface.

Fig. 9
figure 9

a–d Simulation results of alloying element (Cr) views over time in GMA welding

Full size image
Fig. 10
figure 10

Measured alloying element distributions in GMA welding

Full size image

4 Conclusions

Heat and mass transfer in GMA welding could be calculated using the welding models validated. The impact of driving forces on the molten pool was analyzed using the simulation results. The following conclusions can be drawn:

  • For the welding conditions considered in this study, the effect of driving forces on the molten pool analyzed using the radial and vertical velocity components obtained from the simulation results is as follows.

  • For the radial velocity component: Buoyancy ≪ arc pressure < EMF < drag < Marangoni < droplet.

  • For the vertical velocity component: Buoyancy ≪ drag < arc pressure < EMF < Marangoni ≪ droplet.

  • The effect of droplet impingement is absolute in determining the penetration depth. The Marangoni force is less effective, but it can reduce the depth and increase the width to some extent.

  • The distribution of alloying elements (Cr and Ni) is determined by the molten pool flow, and the diffusion effect is negligible. Due to the predominant effect of droplet impingement on the vertical velocity of the molten pool, the element contents are higher at the bottom.