Abstract
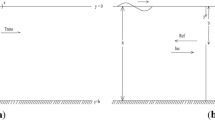
The problem of propagation of obliquely incident surface water waves involving an asymmetric rectangular trench in a channel of finite depth is examined for its solution. The problem under consideration leads to multiple series relations involving trigonometric functions. Instead of converting these relations into systems of integral equations, direct algebraic approaches are utilized and the corresponding solutions are obtained approximately, by way of solving the reduced system of over-determined algebraic equations. The system of over-determined algebraic equations are solved with the aid of the well-known algebraic approaches “Least square” (LS) and “Singular value decomposition” (SVD) methods. The presently determined results involving the reflection and transmission coefficients related to the scattering problem under consideration, agree very well, with the known results obtained recently, where integral equations and their approximate numerical solutions were determined. The effect of system of parameters on hydrodynamics quantities such as reflection and transmission coefficients, wave elevation are analysed and shown through tables and graphs. The present algebraic methods appear to be very direct and quick. A similar techniques are found to be applicable to the problem of scattering of surface water waves by any finite number of asymmetrical placed rectangular trenches. The problem of a pair of asymmetrical trenches is under progress. The energy balance relation for the given problem is derived and used to check the accuracy of numerical results. Some important results such as wave elevation profiles, the singularity behaviour of the flow near trench edges are investigated and analyzed through graphs.









Similar content being viewed by others
References
Bender CJ, Dean RG (2003) Wave transformation by two-dimensional bathymetric anomalies with sloped transitions. Coast Eng 50:61–84
Bhattacharjee J, Soares CG (2010) Wave interaction with a floating rectangular box near a vertical wall with step type bottom topography. J Hydrodyn (Ser B) 22:91–96
Chakraborty R, Mandal BN (2015) Oblique wave scattering by a rectangular submarine trench. ANZIAM J 56:286–298
Das S, Bora SN (2018) Oblique water wave damping by two submerged thin vertical porous plates of different heights. Comput Appl Math 37:3759–3779
Jung TH, Cho YS (2009) Analytical approach for long wave solution to an arbitrarily varying topography. J Coast Res 25:216–223
Kaur A, Martha SC, Chakrabarti A (2019) Solution of the problem of propagation of water waves over a pair of asymmetrical rectangular trenches. Appl Ocean Res 93 (in press)
Kirby JT, Dalrymple RA (1983) Propagation of obliquely incident waves over a trench. J Fluid Mech 133:47–63
Lin P, Liu HW (2005) Analytical study of linear-wave reflection by a two-dimensional obstacle of general trapezoidal shape. J Eng Mech 131:822–830
Liu Y, Li YC, Teng B (2007) Wave interaction with a new type perforated breakwater. Acta Mech Sin 23:351–358
Liu Y, Li Y-C, Teng B (2012) Interaction between obliquely incident waves and an infinite array of multi-chamber perforated caissons. J Eng Math 74:1–18
Liu HW, Yang J, Lin P (2012) An analytic solution to the modified mild-slope equation for wave propagation over one-dimensional piecewise smooth topographies. Wave Motion 49:445–460
Liu HW, Fu DJ, Sun XL (2013) Analytic solution to the modified mild-slope equation for reflection by a rectangular breakwater with scour trenches. J Eng Mech 139(1):39–58
Liu HW, Luo J-X, Lin P, Liu R (2013) Analytical solution for long-wave reflection by a general breakwater or trench with curvilinear slopes. J Eng Mech 139:229–245
Mei CC (1989) The applied dynamics of ocean surface waves. World Scientific, Singapore
Meng Q, Lu DQ (2017) Hydro-elastic interaction between water waves and thin elastic plate floating on three-layer fluid. Appl Math Mech 38:567–584
Miles JW (1982) On surface-wave diffraction by a trench. J Fluid Mech 115:315–325
Milller KS (1973) Complex linear least squares. SIAM Rev 15(4):706–726
Roy R, Chakraborty R, Mandal BN (2016) Propagation of water waves over an asymmetrical rectangular trench. Q J Mech Appl Mech 70:49–64
Strang G (1998) Intrduction to linear algebra, 3rd edn. Wellesley-Cambridge Press, Wellesley
Wang CD, Meylan MH (2002) The linear wave response of a floating thin plate on water of variable depth. Appl Ocean Res 24:163–174
Xie JJ, Liu HW (2012) An exact analytic solution to the modified mild-slope equation for waves propagating over a trench with various shapes. Ocean Eng 50:72–82
Xie JJ, Liu HW, Lin P (2011) Analytical solution for long-wave reflection by a rectangular obstacle with two scour trenches. J Eng Mech 137:919–930
Acknowledgements
Amandeep Kaur is thankful to the Department of Science and Technology, Govt. of India, for inspire grant for pursuing Ph.D. degree at the Indian Institute of Technology Ropar, India. A. Chakrabarti is grateful to NASI for financial support in the form of NASI Honorary-Scientist (Reference Number: NAS/1022/1/2015-16).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Raphaèle Herbin.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Kaur, A., Martha, S.C. & Chakrabarti, A. An algebraic method of solution of a water wave scattering problem involving an asymmetrical trench. Comp. Appl. Math. 39, 229 (2020). https://doi.org/10.1007/s40314-020-01255-y
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40314-020-01255-y
Keywords
- Over-determined system
- Least squares method
- Singular value decomposition method
- Asymmetric rectangular trench
- Hydrodynamics quantities