1 Introduction

The fractional calculus was originated in 1695 as a generalization of the integer order calculus. This happened through a question asked by L’Hospital to Leibniz about the meaning of \(\frac{\mathrm{d}^n}{\mathrm{d}x^n}\), being \(n=\frac{1}{2}\). In this way, it is possible to define integrals and derivatives with arbitrary orders. Since its inception, many contributions have been made by several researchers, including famous names such as Euler, Lagrange, Laplace, Fourier, Abel and Liouville (Camargo and Oliveira 2015; Srivastava and Saxena 2001).

This calculus is one of the most effective current mathematical tools used to model real-world problems. Several definitions have been proposed for fractional integrals, for example, the fractional integrals of Liouville, Weyl and Riemann–Liouville. The fractional derivative also has several definitions such as those derived from Riemann–Liouville, Caputo, Liouville, Weyl, Riesz, Grünwald–Letnikov, Marchaud and Hifler (Camargo and Oliveira 2015; Saad et al. 2018). In contrast to the Caputo’s fractional derivative, most fractional derivative definitions do not satisfy the property that the derivative of a constant is null. This suggests a preference for the Caputo derivative in many situations. Other definitions that are also commonly used today are of Riemann–Liouville and Grünwald–Letnikov (Camargo and Oliveira 2015; Pinto and Tenreiro Machado 2014).

This is important because the past is considered to explain the present (Camargo and Oliveira 2015; Pinto and Tenreiro Machado 2014). In Saeedian (2017), El-Saka (2013), a system of fractional differential equations is used to study the effect of memory on epidemic evolution. One type of memory widely observed in ecology and epidemiology is hysteresis. In hysteresis, the current state of the system depends not only on current conditions but also on previous conditions, that is, past events influence the current dynamics (Beisner et al. 2008; Chen et al. 2017; Pimenov 2012; Yamana et al. 2017). In Pimenov (2012), the hysteresis effect is incorporated into the biological model since the defense mechanism of certain living beings is activated. For example, in a situation of spreading of an infectious disease for human beings, depending on type of disease, previous experiences can reveal that social distance or additional hygiene habits are defensive behaviors to prevent its propagation. The vaccine can also have a long-term memory effect, when it has a lasting effect, causing the body to defend itself through immune memory.

Specifically, as in Beisner et al. (2008), Yamana et al. (2017), in this manuscript, we consider the effect of hysteresis on the spread of the disease through the influence of all previous states in the current states of the dynamics. To illustrate the potential of fractional differential equations in epidemiological processes with hysteresis, we investigate the evolution of COVID-19 in a population. Since the spread of COVID-19 occurs through contact between infected individuals and susceptible individuals, with part of the population already recovered, we employ the famous epidemiological SIR (susceptible–infected–recovered) model, which is compartmental model proposed by Kermack and McKrendick in 1927 and is mathematically described by a system of first order differential equations (Edelstein-Keshet 1988). However, due to the fact that this disease is little known and under-reported, parameters such as speed of propagation and recovery and contact rates are difficult to estimate. Consequently, its modeling using classical differential equations can be inappropriate to represent the dynamics of the populations involved. This is still another justification for adopting fractional equations since it is possible to adjust the order of the differential equation to the real data of the spread of the disease.

The rates of transmission and recovery (and, consequently, the time that individuals remain infected, since this time is the inverse of the recovery rate \( \gamma \)) were estimated from the actual data on the number of infected individuals in each country studied. We obtain numerical solutions since the used (SIR) model is non-linear. With these parameters in hand, it is possible to make projections for new numbers of cases in the future days.

The work is organized as follows. In Sect. 2, we present some definitions necessary for the mathematical development of the work. Section 3 shows two reasons for the use of fractional calculus, namely the Tautochrone problem and the memory effect. In Sect. 4, we present the main results of the work, where we verify objectively the memory effect via statistical tools and analyse the contribution of historical values to the fractional operators. Finally, Sect. 5 presents the fractional epidemiological SIR model to describe the evolution of COVID-19 in several countries. By adjusting the model to the data, it was possible to see that fractional calculus is a good tool for modelling real phenomena. Furthermore, the fractional order of the derivative indicates whether the disease spreads more quickly or more slowly in a given country.

2 Preliminary

In this section, we recall some of the main results of the fractional calculus needed in this work.

Definition 1

Let \(\alpha \in \mathbb {R}^+, b>0\) and \(f \in L^p([0,b]:\mathbb {R}^m)\), with \(1\le p\le \infty \). The fractional integral of Riemann–Liouville, for \(t \in [0,b],\) of order \(\alpha \), is given by

$$\begin{aligned} J^\alpha _t f(t) = \dfrac{1}{\varGamma (\alpha )} \int _{0}^{t} (t-s)^{\alpha -1}f(s)\mathrm{d}s. \end{aligned}$$
(1)

When \( \alpha \in \mathbb {N} \), we have \( \varGamma (\alpha ) = \alpha ! \) In this case, Eq. (1) becomes the Cauchy formula for iterated integrals, which is the motivation for this definition. Furthermore, for \( \alpha > 0 \), the integral exists for almost every t in [0, b] .

We denote by \( AC^n[0, b] \) the set of functions in which the order derivative \( n-1 \) is absolutely continuous in [0, b] (Diethelm 2010).

Definition 2

Let \(\alpha \in \mathbb {R}^+, b>0\), \(f \in AC^n[0,b]\) and \(n=\lfloor \alpha \rfloor \). The fractional derivative of Riemann–Liouville of order \(\alpha \) is given by

$$\begin{aligned} D^\alpha _t f(t) = D^n_t J_t^{n-\alpha } f(t) = \dfrac{\mathrm{d}^n}{\mathrm{d}t^n} \left( \dfrac{1}{\varGamma (n-\alpha )} \int _{0}^{t} (t-s)^{n-\alpha -1}f(s)\mathrm{d}s \right) . \end{aligned}$$
(2)

Definition 3

Let \(\alpha \in \mathbb {R}^+, b>0\) and \(f \in AC^n[0,b]\). For \(t \in [0,b]\), the fractional derivative of Caputo of order \(\alpha \) is given by

$$\begin{aligned} cD^\alpha _t f(t)= & {} D^\alpha _t (f(t) - f(0)). \end{aligned}$$
(3)

For \( \alpha \in (0,1)\), one can show that

$$\begin{aligned} cD^\alpha _t f(t) = J_t^{1-\alpha }f'(t). \end{aligned}$$
(4)

Next, we present some important statistics concepts for the development of the work.

Definition 4

A random variable X follows the beta distribution if its probability density function is given by

$$\begin{aligned} f_X(x) = f_X(x; p, q) = \dfrac{1}{B(p,q)} x^{p-1}(1-x)^{q-1} I_{(0,1)}(x), \end{aligned}$$
(5)

where \(p,q > 0\) and \(I_{(0,1)}\) the indicator function of interval (0, 1).

Remark 1

When \( p = q = 1\) the beta distribution becomes the uniform distribution over the range (0, 1).

The expectation or expected value represents the mean of random variable X. Below, we present the definition of this concept for continuous random variable.

Definition 5

(Mood and Graybill 1974) Let X be a continuous random variable with the probability density function \( f_X(\cdot ) \). The expectation or expected value of X is given by

$$\begin{aligned} E[X] = \int _{-\infty }^{\infty } x f_X(x) \mathrm{d}x. \end{aligned}$$
(6)

Proposition 1

(Mood and Graybill 1974) Let \(g: \mathbb {R} \rightarrow \mathbb {R}\) and X be a continuous random variable with the probability density function \( f_X(\cdot ) \). The expectation or expected value of g(X) is given by

$$\begin{aligned} E[g(X)] = \int _{-\infty }^{\infty } g(x) f_X(x) \mathrm{d}x. \end{aligned}$$
(7)

3 Motivations for using fractional calculus

The fractional or non-integer order calculus adds information to the classical calculus, with a more accurate description of certain natural phenomena. It can be applied to several areas of knowledge, such as physics, chemistry, engineering, technology, among others (Herrmann 2013; Li et al. 2011; Silva et al. 2004; Saad et al. 2018). In this section, we present two motivations for the use of fractional calculus: the tautochrone problem and the effect of memory in biological models.

3.1 The tautochrone problem

The tautochrone problem (or isochronic curve) corresponds to finding a curve s for which an object spends the same time to slide though the curve for any starting point \(y_0\) to 0. The path is considered to be frictionless and under uniform gravity. In 1823, Abel solved this problem using fractional calculus. The equation that describes the object descent time is given by Camargo and Oliveira (2015)

$$\begin{aligned} \tau = \dfrac{1}{\sqrt{2g}} \int _0^{y_0} (y-y_0)^{-\frac{1}{2}} \left( \dfrac{\mathrm{d}s}{\mathrm{d}y}\right) \mathrm{d}y, \end{aligned}$$
(8)

where g is gravity, y(t) is the height of the object at time t, \( y_0 \) is the initial height at which the object was launched, and s is the desired curve given as a function of y (Camargo and Oliveira 2015).

The curve s can be found using the traditional calculus by applying the Laplace transform and the Convolution Theorem (Camargo and Oliveira 2015). Abel obtained the same solution using fractional calculus. In particular, he observed that except for the multiplication by \(1/\varGamma (\frac{1}{2})\) Eq. (8) corresponds to the fractional integral of order \( \frac{1}{2} \) of the function \(s'(y)\). Thus, one can easily obtain the desired solution if the fractional derivative of the constant \( \tau \) is known (Camargo and Oliveira 2015).

3.2 Memory effect: traditional approach

As stated in Sect. 1, fractional calculus is a great tool that can be employed to describe real-life phenomena with so-called memory effect.

Classic models of autonomous ordinary differential equations have no memory, because their solution does not depend on the previous instant. For instance, if \(f(t;x_0)\) is a solution of an autonomous first-order ordinary differential equation with the initial condition \(x_0\) at \(t=0\), then we have the flow property \(f(t+s; x_0) = f(t;f(s;x_0))\), which means that the solution does not change by considering \(f(s;x_0)\) as initial condition since \(f(s;x_0)\) belongs to the solution. Thus, given an initial value, the solution is uniquely determined for any point of domain. In general, this assertion is not true for fractional differential equations. One way to introduce the memory effect into a mathematical model is to change the order of the derivative of a classical model so that it is non-integer (Diethelm 2010; Saeedian 2017).

Let f be a real function defined in [0, t] , \( t_1, t_2 \in [0, t] \) are such that \( 0<t_1 <t_2 \), and \( H = (J^\alpha f) (t_2) - (J^\alpha f) (t_1 ) \) for \( \alpha \in \mathbb {R}^+\). From equalities below, one can observe that the value of H depends on the entire range of f over \( [0, t_2] \) if \(\alpha \ne 1 \), whereas H depends only on the range of f over \( [t_1, t_2] \) if \(\alpha = 1\):

$$\begin{aligned} H= & {} (J^\alpha f) (t_2) - (J^\alpha f) (t_1 ) \nonumber \\= & {} \dfrac{1}{\varGamma (\alpha )} \left[ \int _0^{t_2} (t_2 - s)^{\alpha -1} f(s) \mathrm{d}s - \int _0^{t_1} (t_1 - s)^{\alpha -1} f(s) \mathrm{d}s \right] \nonumber \\= & {} \dfrac{1}{\varGamma (\alpha )} \left[ \int _{t_1}^{t_2} (t_2 - s)^{\alpha -1} f(s) \mathrm{d}s + \int _0^{t_1} \left[ (t_2 - s)^{\alpha -1} - (t_1 - s)^{\alpha -1}\right] f(s) \mathrm{d}s \right] . \end{aligned}$$
(9)

Note that if \(\alpha =1\), then the second integral is canceled:

$$\begin{aligned} H= & {} \dfrac{1}{\varGamma (\alpha )} \int _{t_1}^{t_2} (t_2 - s)^{\alpha -1} f(s) \mathrm{d}s = \int _{t_1}^{t_2} f(s) \mathrm{d}s. \end{aligned}$$
(10)

In contrast, the second integral is not canceled if \( \alpha \ne 1 \). From (9), we can see that H depends on what happens in \([0,t_1]\) and \( [t_1, t_2] \). Thus, for \(\alpha \ne 1\), H depends on the entire range of f over \( [0, t_2] \). Therefore, the fractional integral in the interval \( [t_1, t_2] \) is not determined by itself, it depends on what happened before \( t_1 \) which characterizes the memory effect in the process.

Next, we study the memory effect in the fractional integral and in the derivatives of Liouville and Caputo. For this purpose, we use the notion of mathematical expectation which is a generalization of the arithmetic mean of observed data.

4 Statistical approach

In this section, we present the so-called memory effect in fractional calculus based on statistical expectation, to the best of our knowledge, which has not yet been presented in the literature. Here, we focus on the Riemann–Liouville integral and Riemann–Liouville and Caputo fractional derivatives of a f function.

4.1 Fractional operators

We begin this section with the proposition below, which characterizes three well-known fractional operators depending on expected values of certain random variables. This result shows most clearly by means of mathematical expectation the so-called memory effect in fractional calculus.

Proposition 2

Let \(\alpha \in \mathbb {R}^+\) and \(f\in AC[0,b]\). Under these conditions, we have

$$\begin{aligned} J_t^\alpha f(t)= & {} \dfrac{t^\alpha }{\varGamma (\alpha + 1)} E[f(tU)]; \end{aligned}$$
(11)
$$\begin{aligned} D_t^\alpha f(t)= & {} \dfrac{t^{-\alpha }}{\varGamma (1-\alpha )} E[f(tW)] + \dfrac{t^{1-\alpha }}{\varGamma (3-\alpha )} E\left[ f'(tV)\right] , \, \, \, \text {if} \, \, \, 0< \alpha < 1; \end{aligned}$$
(12)
$$\begin{aligned} cD_t^\alpha f(t)= & {} \dfrac{t^{1-\alpha }}{\varGamma (2-\alpha )} E\left[ f'(tW) \right] , \, \, \, \text {if} \, \, \, 0< \alpha < 1, \end{aligned}$$
(13)

where U, V and W are random variables with the distributions \( U \sim B(1, \alpha ), V \sim B(2,1- \alpha ) \) and \( W \sim B(1,1- \alpha ) \).

Proof

First, note that \(B(1,\alpha )=\dfrac{1}{\alpha }\).

From (1), we have

$$\begin{aligned} J_t^\alpha f(t)=\dfrac{1}{\varGamma (\alpha )} \int _{0}^{t} (t-s)^{\alpha -1}f(s)\mathrm{d}s=\dfrac{1}{\varGamma (\alpha )} \int _{0}^{t} t^{\alpha -1}\left( 1-\dfrac{s}{t}\right) ^{\alpha -1}f(s)\mathrm{d}s. \end{aligned}$$

Let \(u=\frac{s}{t}\), we obtain

$$\begin{aligned} J_t^\alpha f(t)= & {} \dfrac{t^{\alpha }}{\varGamma (\alpha )} \int _{0}^{1} \left( 1-u\right) ^{\alpha -1}f(tu) \mathrm{d}u \nonumber \\= & {} \dfrac{t^{\alpha }B(1,\alpha )}{\varGamma (\alpha )} \int _{0}^{1} \dfrac{\left( 1-u\right) ^{\alpha -1}}{B(1,\alpha )} f(tu) \mathrm{d}u \nonumber \\= & {} \dfrac{t^{\alpha }}{\alpha \varGamma (\alpha )} \int _{0}^{1} \dfrac{\left( 1-u\right) ^{\alpha -1}}{B(1,\alpha )} f(tu) \mathrm{d}u. \end{aligned}$$
(14)

By the fact of \( \dfrac{\left( 1-u\right) ^{\alpha -1}}{B(1,\alpha )}\) is the density function of a beta distribution, we have that (11) holds true for \(U \sim B(1,\alpha )\).

Let \(\alpha \in (0,1)\), from (14), we have

$$\begin{aligned} J^{1-\alpha }_t f(t) = \dfrac{t^{1-\alpha }}{\varGamma (1-\alpha )} \int _{0}^{1} \left( 1-u\right) ^{-\alpha }f(tu) \mathrm{d}u. \end{aligned}$$

Since \(B(1,1-\alpha ) = \dfrac{1}{1-\alpha }\) and \(B(2,1-\alpha ) = \dfrac{1}{(1-\alpha )(2-\alpha )}\), the product rule for derivatives reveals that

$$\begin{aligned} D^\alpha _t f(t)= & {} \dfrac{\mathrm{d}}{\mathrm{d}t} \left[ J^{1-\alpha }_t f(t)\right] \\= & {} \dfrac{(1-\alpha )t^{-\alpha }}{\varGamma (1-\alpha )} \int _{0}^{1} \left( 1-u\right) ^{-\alpha }f(tu) \mathrm{d}u \\&+ \dfrac{t^{1-\alpha }}{\varGamma (1-\alpha )} \int _{0}^{1} \left( 1-u\right) ^{-\alpha }u f'(tu) \mathrm{d}u \\= & {} \dfrac{t^{-\alpha }}{\varGamma (1-\alpha )} \int _{0}^{1} \dfrac{\left( 1-u\right) ^{-\alpha }}{B(1,1-\alpha )}f(tu) \mathrm{d}u \\&+ \dfrac{t^{1-\alpha }}{(1-\alpha )(2-\alpha )\varGamma (1-\alpha )} \int _{0}^{1} \dfrac{\left( 1-u\right) ^{-\alpha }}{B(2,1-\alpha )}u f'(tu) \mathrm{d}u \\= & {} \dfrac{t^{-\alpha }}{\varGamma (1-\alpha )} \int _{0}^{1} \dfrac{\left( 1-w\right) ^{-\alpha }}{B(1,1-\alpha )}f(tw) \mathrm{d}w \\+ & {} \dfrac{t^{1-\alpha }}{(1-\alpha )(2-\alpha )\varGamma (1-\alpha )} \int _{0}^{1} \dfrac{v\left( 1-v\right) ^{-\alpha }}{B(2,1-\alpha )} f'(tv) \mathrm{d}v \\= & {} \dfrac{t^{-\alpha }}{\varGamma (1-\alpha )} E[f(tW)] + \dfrac{t^{1-\alpha }}{\varGamma (3-\alpha )} E[f'(tV)], \end{aligned}$$

where \(W \sim B(1,1-\alpha )\) and \(V \sim B(2,1-\alpha )\). Note that the beta function is well defined since \(\alpha \in (0,1)\). Thus, we prove (12).

Finally, from (4), we have

$$\begin{aligned} cD^\alpha _t f(t)= & {} J_t^{1-\alpha }f'(t) \nonumber \\= & {} \dfrac{1}{\varGamma (1-\alpha ) } \int _0^t (t-s)^{-\alpha } f'(s) \mathrm{d}s \nonumber \\= & {} \dfrac{1}{\varGamma (1-\alpha ) } \int _0^t t^{-\alpha } \left( 1-\dfrac{s}{t}\right) ^{-\alpha } f'(s) \mathrm{d}s \nonumber \\= & {} \dfrac{1}{\varGamma (1-\alpha ) } \int _0^1 t^{1-\alpha } \left( 1-u\right) ^{-\alpha } f'(tu) \mathrm{d}u \nonumber \\= & {} \dfrac{t^{1-\alpha }}{\varGamma (1-\alpha ) } B(1,1-\alpha ) \int _0^1 \dfrac{\left( 1-u\right) ^{(1-\alpha )-1}}{B(1,1-\alpha )} f'(tu) \mathrm{d}u\nonumber \\= & {} \dfrac{t^{1-\alpha }}{(1-\alpha )\varGamma (1-\alpha ) } \int _0^1 \dfrac{\left( 1-w\right) ^{(1-\alpha )-1}}{B(1,1-\alpha )} f'(tw) \mathrm{d}w \nonumber \\= & {} \dfrac{t^{1-\alpha }}{\varGamma (2-\alpha ) } E[f'(tW)], \end{aligned}$$
(15)

where \(W \sim B(1,1-\alpha )\). Thus, we conclude that (13) holds true.

Remark 2

Note that, by Definition 3, exchanging f(t) by \( f(t) - f(0) \) or, equivalently, f(tW) by \( f(tW) - f(0) \) in (12), for \( 0<\alpha <1 \), we can rewrite Caputo’s derivative as follows:

$$\begin{aligned} cD^\alpha _t f(t) = \dfrac{t^{-\alpha }}{\varGamma (1-\alpha )} E[f(tW) - f(0)] + \dfrac{t^{1-\alpha }}{\varGamma (3-\alpha )} E\left[ f'(tV)\right] . \end{aligned}$$
(16)

We can see that (16) coincides with (13). This follows from the pf of Proposition 2 and Definitions (3) and (4) .

Remark 3

Note that, for \(0< \alpha < 1, cD^\alpha f(t_\alpha )=0 \) does not imply \(t_\alpha \) is a maximum (or minimum) point of f. In fact, suppose that f has just only local maximum in \(t^*\).

In this case, we have \(f'(s) > 0\) for all \(s < t^*\). This implies that \(E[f'(tW)]>0\) for all \(t\le t^*\). Thus, by (13), if

\(cD^\alpha f({t}_\alpha ) = 0\) then \({t}_\alpha > t^*\). That is, \(cD^\alpha f({t}_\alpha ) = 0\) but \({t}_\alpha \) is not the maximum point of f.

Next, we provide some examples of Riemann–Liouville and Caputo fractional derivatives using the formulas (12) and (13).

Example 1

If \(f(t)=k\), where k is constant, we have \(E[f(tW)] = E[k] = k\) and \(E[f'(tV)] = E[f'(tW)]= E[ 0 ] = 0\). Thus, from (12) we have \(D^\alpha _t f(t) = \dfrac{k t^{-\alpha }}{\varGamma (1-\alpha )}\), and from (13) we have \(cD^\alpha _t f(t)=0\).

Example 2

If \(f(t) = t^\gamma \), with \(\gamma \in (-1,\infty )\), we find \(D^\alpha _t f(t)\) and \(cD^\alpha _t f(t)\). Note that

$$\begin{aligned} E[f(tW)]= & {} \int _0^1 \dfrac{(1-w)^{-\alpha }}{B(1,1-\alpha )} (tw)^\gamma \mathrm{d}w \\= & {} t^\gamma (1-\alpha ) \int _0^1 (1-w)^{-\alpha } w^\gamma \mathrm{d}w \\= & {} t^\gamma (1-\alpha ) B(\gamma +1,1-\alpha ), \end{aligned}$$

and

$$\begin{aligned} E[f'(tV)]= & {} \int _0^1 \dfrac{(1-v)^{-\alpha }v}{B(2,1-\alpha )} \gamma (tv)^{\gamma -1} \mathrm{d}v \\= & {} \dfrac{\gamma t^{\gamma -1}}{B(2,1-\alpha )} \int _0^1 (1-v)^{-\alpha } v^\gamma \mathrm{d}v \\= & {} \dfrac{\gamma t^{\gamma -1}}{B(2,1-\alpha )} B(\gamma +1,1-\alpha ). \end{aligned}$$

From (12), we have

$$\begin{aligned} D^\alpha _t f(t)= & {} \dfrac{t^{-\alpha }}{\varGamma (1-\alpha )} t^\gamma (1-\alpha ) B(\gamma +1,1-\alpha ) \nonumber \\&+ \dfrac{t^{1-\alpha }}{\varGamma (3-\alpha )} \dfrac{\gamma t^{\gamma -1}}{B(2,1-\alpha )} B(\gamma +1,1-\alpha ) \nonumber \\= & {} \dfrac{(1-\alpha )t^{\gamma -\alpha }}{\varGamma (1-\alpha )} B(\gamma +1,1-\alpha ) + \dfrac{\gamma t^{\gamma -\alpha }}{\varGamma (3-\alpha )B(2,1-\alpha )} B(\gamma +1,1-\alpha ) \nonumber \\= & {} t^{\gamma -\alpha } B(\gamma +1,1-\alpha ) \left[ \dfrac{1-\alpha }{\varGamma (1-\alpha )} + \dfrac{\gamma }{\varGamma (3-\alpha )B(2,1-\alpha )}\right] \nonumber \\= & {} t^{\gamma -\alpha } \dfrac{\varGamma (\gamma +1)\varGamma (1-\alpha )}{\varGamma (2+\gamma -\alpha )} \left[ \dfrac{1-\alpha }{\varGamma (1-\alpha )} + \dfrac{\gamma \varGamma (3-\alpha ) }{\varGamma (3-\alpha )\varGamma (2)\varGamma (1-\alpha )}\right] \nonumber \\= & {} t^{\gamma -\alpha } \dfrac{\varGamma (\gamma +1)\varGamma (1-\alpha )}{\varGamma (2+\gamma -\alpha )} \left[ \dfrac{1-\alpha }{\varGamma (1-\alpha )} + \dfrac{\gamma }{\varGamma (1-\alpha )}\right] \nonumber \\= & {} t^{\gamma -\alpha } \dfrac{\varGamma (\gamma +1)}{\varGamma (2+\gamma -\alpha )} \left[ 1 + \gamma -\alpha \right] \nonumber \\= & {} t^{\gamma -\alpha } \dfrac{\varGamma (\gamma +1)}{(1+\gamma -\alpha )\varGamma (1+\gamma -\alpha )} \left[ 1 + \gamma -\alpha \right] \nonumber \\= & {} t^{\gamma -\alpha } \dfrac{\varGamma (\gamma +1)}{\varGamma (1+\gamma -\alpha )}. \end{aligned}$$
(17)

Furthermore,

$$\begin{aligned} E[f'(tW)]= & {} \int _0^1 \dfrac{(1-w)^{-\alpha }}{B(1,1-\alpha )} \gamma (tw)^{\gamma -1} \mathrm{d}w \\= & {} \dfrac{\gamma t^{\gamma -1}}{B(1,1-\alpha )} \int _0^1 (1-w)^{-\alpha } w^{\gamma -1} \mathrm{d}w \\= & {} \dfrac{\gamma t^{\gamma -1}}{B(1,1-\alpha )} B(\gamma ,1-\alpha ). \end{aligned}$$

Replacing in (13), we obtain

$$\begin{aligned} cD^\alpha _t f(t)= & {} \dfrac{t^{1-\alpha }}{\varGamma (2-\alpha )} \dfrac{\gamma t^{\gamma -1}}{B(1,1-\alpha )} B(\gamma ,1-\alpha ) \nonumber \\= & {} \dfrac{t^{1-\alpha }}{\varGamma (2-\alpha )} \dfrac{\gamma t^{\gamma -1}\varGamma (2-\alpha )}{\varGamma (1)\varGamma (1-\alpha )} \dfrac{\varGamma (\gamma )\varGamma (1-\alpha )}{\varGamma (1+\gamma -\alpha )}\nonumber \\= & {} t^{1-\alpha } t^{\gamma -1} \dfrac{\gamma \varGamma (\gamma )}{\varGamma (1+\gamma -\alpha )}\nonumber \\= & {} t^{\gamma -\alpha } \dfrac{\varGamma (\gamma +1)}{\varGamma (1+\gamma -\alpha )}. \end{aligned}$$
(18)

The results of Examples 1 and 2 coincide with those presented in the literature, showing that Eqs. (12) and (13) can be used instead of the traditional approach to fractional calculus. Moreover, in Example 2, Eqs. (17) and (18) are the same, which is correct since \( D^\alpha _t f(t) = cD^\alpha _t f(t) \) for \( f(0) = 0 \) and for all \(\alpha \in (0,1)\) (see Eq. (16)).

4.2 The hysteresis phenomenon

When the current state of a system is influenced by the dynamics of its historical past, it is said that such a system presents the phenomenon of hysteresis. Several authors have incorporated effect of hysteresis on biological systems (Beisner et al. 2008; Pimenov 2012; El-Saka 2013; Yamana et al. 2017). In general, hysteresis is a type of non-limited window memory (that is, limited from the origin), so it can be formulated mathematically with a convolution kernel from the origin. This is a typical kernel used to define integral and differential fractional operators, such as the Caputo derivative. It is also possible to notice from formulas (1) and (4) that the kernel involved reveals that the memory of more recent times has more influence than the memory of previous times. This is in agreement with the evolutionary epidemiological systems (Saeedian 2017). Our study goes further. It reveals that fractional operators can be interpreted from the statistical approach, through mathematical expectation, where the past history of the system follows a beta distribution. Since the parameter \(\alpha \) is between 0 and 1, recent times have more influence than previous times in this distribution.

The hysteresis effect interpreted by fractional operators is shown in formulas (11)–(13). More specifically, the variation rate in the Caputo derivative is explicitly given by the weighted average of all past derivatives as we can see in the formula (11). The other operators have similar explanations.

Since U has distribution \( B(1, \alpha ) \), the random variable \( S = tU \) assumes the values in the interval (0, t) . Thus, from (11), \( J_t^\alpha f(t) \) coincides with \( \frac{t^\alpha }{\varGamma (\alpha + 1)} E [f(S)] \), \( 0 \le s \le t \). Clearly, \( J_t^\alpha f(t) \) is affected by all prior values at t because the expected value E[f(S)] is also affected. Since E[f(S)] appears in (12) and (16), it follows that \(D_t^\alpha f(t) \) and \(cD_t^\alpha f(t)\) also have a memory effect.

The formulas (11)–(13) reveal interesting interpretations:

  1. 1)

    The fractional integral \(J_t^\alpha f(t)\) is proportional to the weighted average of f(s), considering all prior values s of t, distributed according to a beta distribution;

  2. 2)

    \(D_t^\alpha f(t)\) is the sum of two amounts proportional to the weighted average of the f(s) and \( f'(s) \) functions, considering all prior values s of t distributed according to a beta distribution;

  3. 3)

    \(cD_t^\alpha f(t)\) is proportional to the weighted average of the classic derivative \( f '(s) \), considering all prior values s less than t, distributed according to a beta distribution;

  4. 4)

    If \(\alpha =1\), then \(U\sim B(1,1)\), that is, U has uniform distribution so that \(J^\alpha _t f(t) =tE[f(tU)]=\int _{0}^{t}f(s) \mathrm{d}s\). Thus, \(D^\alpha _t f(t)=\dfrac{\mathrm{d}}{\mathrm{d}t}J^0_t f(t) = \dfrac{\mathrm{d}}{\mathrm{d}t}f(t) = f'(t)\) and \(cD^\alpha _t [f(t)-f(0)]=\dfrac{\mathrm{d}}{\mathrm{d}t}J^0_t [f(t)-f(0)] = \dfrac{\mathrm{d}}{\mathrm{d}t}[f(t)-f(0)] = f'(t)\). Consequently, the fractional calculus coincides with the classic one, when \(\alpha =1\).

Items 1), 2) and 3) indicate that the values of the fractional integral, as well as the fractional derivatives in t, are affected by the historical values of f (at every time before t). Thus, the fractional calculus seems to be a more adequate mathematical tool for modeling phenomena with hysteresis than the classical calculus (that is, for the case where \(\alpha =1\)).

4.3 Influence of beta distribution on fractional operators of order \(\alpha \)

Since each historical value (before t) acts differently for fractional operators, according to the distributions \( B(1, \alpha ), B(1,1- \alpha ) \) and \( B(2, 1- \alpha ) \), we investigate which ones contribute most to these operators in relation to the order \( \alpha \in (0,1) \).

According to formula (11) , the value of \( J^\alpha _t f(t) \) is affected according to the density \( f_U(u) = \dfrac{(1-u)^{\alpha -1}}{B (1, \alpha )} \), which is increasing if \( 0< \alpha <1 \) and decreasing if \( \alpha > 1 \). For \(0< \alpha < 1\), recent values (i.e., close to \( t \Leftrightarrow u \simeq 1 \)) contribute more to the fractional integral \( J_t^\alpha f (t) \) than the remote ones (i.e., close to \(0 \Leftrightarrow u \simeq 0\)). On the other hand, for \( \alpha > 1 \) the opposite occurs.

From formulas (12) and (13) , one can note that Riemann–Liouville and Caputo derivative operators have similar influence of prior values of f to the integral for \( 0< \alpha <1 \). In particular, values close to t contribute more to fractional derivatives than remote values (those ones evaluated for times close to 0). This is due to the fact that density distributions \(f_W(w)=\dfrac{(1-w)^{-\alpha }}{B(1,1-\alpha )}\) and \(f_V(v) = \dfrac{v\left( 1-v\right) ^{-\alpha }}{B(2,1-\alpha )}\) are increasing for \(0< \alpha < 1\).

For the integral operator, the higher the value of \( \alpha \in (0,1) \) is, the more uniform are the weights of the initial and final values, that is, the closer to the uniform distribution the random variable U becomes. For derivative operators, the opposite occurs. This is illustrated in Fig. 1. Note that the density function \( f_U(\cdot ) \), for the parameter \( \alpha \), is equal to the density function \( f_W(\cdot ) \) for the parameter \( 1- \alpha \). The \( f_V(\cdot ) \) density function follows the same pattern as \( f_W (\cdot ) \), but with more accentuated increasing.

Regarding the fractional integral, we notice that the higher the value of \( \alpha \) is the greater is the contribution of remote values (\( u \simeq 0 \)). In contrast, the higher \( \alpha \), the smaller the contribution of the values evaluated close to t (i.e., \( u \simeq 1 \)). As to the Riemann–Liouville and Caputo fractional derivative operators, we obtain an opposite behaviour.

Fig. 1
figure 1

Density functions \( f_U \), \( f_W \) and \( f_V \), for parameters \( \alpha = 0.2, \alpha = 0.5 \) and \( \alpha = 0.8 \). a The distribution of historical weights for fractional integral; b the distribution of historical weights for the Caputo and Riemann–Liouville derivatives; c the distribution that, combined with \( f_W \), defines the historical weights for the Riemann–Liouville derivative

Full size image

Next, we admit the effect of hysteresis in an epidemiological SIR model to study the COVID-19 in four countries: South Korea, China, Switzerland and Italy.

5 Application

In this section, we analyze the spread of COVID-19 in some countries using an epidemiological model of the SIR type. This is a simple compartmental model that was proposed in 1927 by Kermack and McKendrick (1927) and is widely used to study the evolution of some diseases. In Pimenov (2012), authors pointed out that the hysteresis phenomenon should ideally be considered in the analysis of the epidemiological behaviour of diseases due to actions caused by the protective instinct and immunity, that are influenced respectively by memory and the so-called immune memory of the body. Additionally, we found out in the previous section that fractional calculus is capable of describing the hysteresis effect, which is more specific than the memory effect, since it involves the complete historical past to determine the present situation. Since we desire to incorporate the memory effect characterized by hysteresis phenomenon, we use the fractional version of the SIR model.

5.1 The models

In the epidemiological SIR model, the population is divided into three compartments: susceptible, infected and recovered. Susceptible individuals correspond to those exposed to the disease, but not yet infected. Those who have already been infected but are no longer infected and have gained immunity are classified as recovered. Originally, the model is given by

$$\begin{aligned} \left\{ \begin{array}{ccl} S'(t) &{}=&{} - \beta S(t) I(t) \\ I'(t) &{}=&{} \beta S(t) I(t) - \gamma I(t) \\ R'(t) &{}=&{} \gamma I(t) \end{array},\right. \end{aligned}$$
(19)

where S(t) , I(t) and R(t) are the number of susceptible, infected and recovered individuals at instant t, respectively. The parameter \(\beta \) is the transmission rate and \( \gamma \) is the recovery rate (Edelstein-Keshet 1988; Kermack and McKendrick 1927).

In this work, we used the fractional versions of the SIR model, given by Diethelm (2013), as follows:

$$\begin{aligned} \left\{ \begin{array}{ccl} cD^\alpha _t S(t) &{}=&{} - \beta ^\alpha S(t) I(t) \\ cD^\alpha _t I(t) &{}=&{} \beta ^\alpha S(t) I(t) - \gamma ^\alpha I(t) \\ cD^\alpha _t R(t) &{}=&{} \gamma ^\alpha I(t) \end{array},\right. \end{aligned}$$
(20)

where \( cD^\alpha _t X(t) \) is the fractional derivative of Caputo of order \( \alpha \in (0,1) \).

According to Diethelm (2013), the fractional derivative operator \(cD^\alpha _t\) has a dimension \((\text {time})^{-\alpha }\) instead of \((\text {time})^{-1}\), so that, due to dimensional analysis, on the right side of (20) the parameters \(\beta \) and \(\gamma \) must have power \(\alpha \).

The system (20) is nonlinear and for the most fractional differential equations, there are no methods to calculate the exact analytical solution (Diethelm 2010). Thus, the solution of (20) is given just by the numerical method.

5.2 Methodology and numerical solution

To compare the classic and fractional SIR models given respectively in (19) and (20), we take data from active cases of the COVID-19, that is, cases of infected people at the analyzed moment, not accumulated (Worldometers 2020), in each of the countries: South Korea, China, Switzerland and Italy. We consider the numerical solutions for which the functions I of the number of infected which fit the real data in the most appropriate way.

The parameters \( \beta , \gamma \) and, in the fractional case, \(\alpha \), are obtained by minimizing the mean squared error:

$$\begin{aligned} \sum _{i=1}^n (I(t_i)-\mathrm{obs}(t_i))^2, \end{aligned}$$
(21)

where obs is the vector with n real data about COVID-19. The process to obtain the parameters \( \beta , \gamma \) and \( \alpha \) consists of minimizing the error given by the formula (21) where I is a numerical solution of the model (20), and similarly for the model (19) considering \( \alpha = 1 \). First, we define a range of values where the parameters vary and the software tests all possible combinations for the triple \( (\beta , \gamma , \alpha ) \). For each value \( (\beta , \gamma , \alpha ) \) the software finds a numerical solution I and then calculates the error using (21). Thus, it is possible to find the values \( (\beta , \gamma , \alpha ) \) that provide the solution I with the smallest possible error, as it is desired in the data adjustment process. After having done it, we have the solution I that best fits the number of case data for each country studied in this paper. Thus, we can plot the numerical solution curve for future days, making projections of new cases of COVID-19 in that country, as in Figs. 2, 3, 4 and 5. Other examples of how to adjust fractional models can be found in Almeida (2017), Almeida et al. (2016), González-Parra et al. (2014), and Li et al. (2018).

The adjustment is performed twice, one for the model (19), with \( \alpha = 1 \) and other for the model (20), where the 3 parameters are found together. Thus, the values \( \beta \) and \( \gamma \) obtained for (19) may be different from those found for (20).

We consider the values of S, I and R in the range [0, 1]. For the normalization process, the values of the vector obs must be divided by a value N corresponding to the population of the country. We found in our tests that the total population of the country is not a feasible value for N. This is due to the fact that the peak of the obtained solution is much higher than the peak of the data, resulting in an inadequate adjustment for both models. We observe that lower values for N resulted in a good fit of the models. In general, the initial susceptible population to the disease is not all inhabitants (residents) since the first cases occur only in certain regions. Even during the outbreak of the disease, it is not the entire population of the country that comes into contact with an infected individual. In addition, some people may have increased resistance or genetic factors that make contamination unlikely. Thus, it seems feasible that the value of N is, in fact, not as large as the total number of inhabitants in a country. Note that, in the case of the SIR model, the average time that each individual remains infectious is the inverse of the recovery rate, that is, \(1/\gamma \), according to Edelstein-Keshet (1988), Tavares (2017). To choose an appropriate value of N we use the following criterion: the peak of the solutions of the models must present values close to the peak of the data and, mainly, the recovery rate should be such that \( \gamma \in [0.05,0.2]\), according to information on the average period (\(1/\gamma \)) of infectivity by COVID-19 (World Health Organization 2020).

To obtain the numerical solution we have adopted the initial condition \( (S_0, I_0, R_0) \), for both models (19) and (20), considering \( I_0 \) equal to the first value of the normalized real data and \( R_0 = 0 \). Since this model does not consider vital dynamics, we have \( 1 = S + R + I \) and, therefore, \( S_0 = 1-I_0 \). The numerical solution is obtained using the Adams–Bashforth–Moulton PECE predictor–corrector method (Diethelm and Freed 1999).

5.3 Results

In this section, we present the results obtained with the models for the number of infected by COVID-19 for four countries. It is worth pointing out that the objective of this section is to analyze the effectiveness of the SIR models (19) and (20) using COVID-19 data and compare them. The graphs in Figs. 2, 3, 4 and 5 show the real data in dotted line, the red dashed lines represent the solution of the fractional model (that is, with memory), and the black continuous lines are the solutions of the classic model. Finally, Table 1 exhibits the mean squared errors (21) obtained of each model and country as well as the corresponding fractional order \( \alpha \). Table 2 presents the parameters found in our simulations.

In Fig. 2, we can observe the behavior of the infected curve obtained by both models, (19) and (20), in comparison to the real data of COVID-19 in South Korea from February 15 to July 31, 2020, where we consider \(N=25{,}000\).

Fig. 2
figure 2

Solutions of the (19) and (20) models in the description of the spread of COVID-19 in South Korea. For the model (19), we use \(\beta =0.4047\) and \(\gamma =0.1071\). For the model (20), we use \(\beta =0.5499\), \(\gamma =0.1055\) and \(\alpha = 0.7607\)

Full size image

Note that the data curve is flatter and wider than that given by the classic SIR model, that is, the disease occurs over a period of time longer than that described by the model. In this case, the fractional solution fits better the data due to the freedom of the parameter \( \alpha \) (that is associated with memory effect). In this example, we can see how the fractional model contributes to a better description of the phenomenon. Table 1 corroborates this fact showing that the mean squared error obtained by the fractional models is less than the one obtained by the classic models.

Figure 3 shows the solutions of the fractional and classic models in comparison to the COVID-19 data of China from January 22 to July 31, 2020. In these simulations, we consider \(N=175000\).

Fig. 3
figure 3

Solutions of the (19) and (20) models in the description of the spread of COVID-19 in China. For the model (19), we use \(\beta =0.3591\) and \(\gamma =0.0907\). For the model (20), we use \(\beta =0.3613\), \(\gamma =0.0907\) and \(\alpha = 0.9937\)

Full size image

In Fig. 3, the fractional model (20) did not present much difference from the classic model (19) . In fact, we can see in Table 1 that the mean squared errors are the same for both models. In this case, the outbreak of the disease occurred in a short period of time, which is already well described by the classic model.

In Fig. 4, we compare the models by analyzing the disease data in Switzerland from February 25 to July 31, 2020, where we consider \(N=45000\).

Fig. 4
figure 4

Solutions of the (19) and (20) models in the description of the spread of COVID-19 in Switzerland. For the model (19), we use \(\beta =0.4349\) and \(\gamma =0.1207\). For the model (20), we use \(\beta =0.5118\), \(\gamma =0.1196\) and \(\alpha = 0.8391\)

Full size image

Again, in Fig. 4, we can note that the fractional model fits the data better than the classic one. This can also be observed in Table 1. The dotted curve is wider with a slower decay than the one produced by the classic SIR model. This fact can best be modeled when there is a memory effect.

In Fig. 5, we compare the models using data of Italy from February 15 to July 31, where we consider \(N=600{,}000\). From Table 1, we can observe that this is another example where the use of the fractional model yielded solutions with mean squared error less than the one produced by the classical model.

Fig. 5
figure 5

Solutions of the (19) and (20) models in the description of the spread of COVID-19 in Italy. For the model (19), we use \(\beta =0.3067\) and \(\gamma =0.1165\). For the model (20), we use \(\beta =0.4628\), \(\gamma =0.1218\) and \(\alpha =0.7114\)

Full size image

It is worth noting that the peaks obtained (in \(t=\bar{t}\)) with the solutions of the model (20) are closer to reality than the solutions of the model (19) in all countries. Moreover, all peaks of all solutions of the model (20) are on the left of the ones of the model (19) according to Remark 3, since \(cD^\alpha I(\bar{t})=0\) for all \(0< \alpha < 1\).

Table 1 exhibits the mean squared errors calculated according to Eq. (21) for the classical and fractional models in relation to the COVID-19 data from South Korea, China, Switzerland and Italy. For each country, the order \( \alpha \) obtained for the fractional derivative is also shown in Table 1.

Table 1 Mean squared errors (MSEs) achieved by the classical and fractional models and the corresponding order \(\alpha \) of the fractional derivative for each country
Full size table

Finally, Table 2 presents the parameters used for the models (19) and (20) for each country.

Table 2 Parameters of fractional model (20) and classical model (19)
Full size table

In Figs. 2, 3, 4 and 5, the solutions of both models (19) and (20) were extended by thirty days, predicting the spread of the disease for another month. Using the best adjustment provided by the fractional model, it is possible to make more accurate predictions about the disease behavior and the peak value.

We also have observed that the order \( \alpha \) of the fractional model indicates whether the disease spreads more quickly or more slowly in a given country. In our simulations, we noticed that the outbreak occurs in a short period of time when \( \alpha \) approaches 1. On the other hand, the more \( \alpha \) approaches 0, the longer the period of time that outbreak occurs. For instance, in China, there was rapid action to control the disease and isolate individuals, making the disease spread more quickly, in less time. This was well described by the high value of \( \alpha \). In contrast, we see that in other countries the disease spreads in a slower rate, taking longer to complete all stages of the disease. For these countries, we obtain lower values for \( \alpha \).

5.4 Numerical solutions for weighted data

In this section, we detail in a more illustrative way the comments made in Sect. 4.3 regarding the influence of the historical values on the fractional operators and the fractional-order \(\alpha \in (0,1)\). Specifically, in Sect. 4.3, we argue that the higher the contribution of the first data is (\(u \simeq 0\)), the lower the order \(\alpha \) of the Caputo derivative is. On the other hand, the higher the contribution of the latest data is (\(u \simeq 1\)), the higher the order \(\alpha \) of the Caputo derivative is. To illustrate the influence of these weights on the model (20), we focus only on data from Switzerland.

Here, the methodology for finding numerical solutions is analogous to the one described in Sect. 5.2, but we modify the formula (21) as follows:

$$\begin{aligned} \sum _{i=1}^n w_i[(I(t_i)-\mathrm{obs}(t_i))^2], \end{aligned}$$
(22)

where \(w_i \in \mathbb {R}\) is the weight assigned to the data. Here, we adopt

  1. (i)

    \(w_i=\dfrac{2(n+1-i)}{n(n+1)}, \, \, i=1,\ldots ,n\), when the greatest weight is attributed to the first data.

  2. (ii)

    \(w_i=\dfrac{2i}{n(n+1)}, \, \, i=1,\ldots ,n\), when the greatest weight is attributed to the latest data;

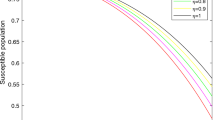
In our simulations in Sect. 5.3 for Switzerland, we obtain \( \alpha = 0.6149 \) as the fractional order of the derivative, according to the model (20). By considering the weights \(w_i\) given as in Item (i), that is, the highest weights attributed to the first data, we obtain \( \alpha = 0.5596 \) as the order of the derivative for the fractional model. As expected, the value of the derivative order decreased. Figure 6 exhibits the numerical solution for this case.

Fig. 6
figure 6

Solution of the SIR model (20) for spreading of COVID-19 with parameter estimation using weights given as in Item (i)

Full size image

In Fig. 7, the parameters are adjusted with the highest weight attributed to the latest data, that is, according to Item (ii). In this case, we obtain \( \alpha = 0.6310 \) for the derivative order of the fractional model. Again as expected, the value \(\alpha \) increased in comparison to the adjustment made in Sect. 4.3.

Fig. 7
figure 7

Solution of the SIR model (20) for spreading of COVID-19 with parameter estimation using weights given as in Item (ii)

Full size image

Given the importance of COVID-19, we will make a preliminary study on new waves, although it is not the main focus of our study. For this new wave, we estimate new peaks taking into account solely the government control actions such as social distance and lockdown. Such actions produce changes in the parameters of the SIR model and, consequently, in the peaks of each wave. In this sense, the SIR model is not only seen as a dynamic system, it comes to be seen as a system with control.

5.5 Control in the SIR model

From the SIR model, we have (Patrão and Reis 2020)

$$\begin{aligned} I = -S + \left( \frac{\gamma }{\beta }\right) \log {S} + k, \end{aligned}$$
(23)

where \(k\in \mathbb {R}\). By (23), for \(S^*=\frac{\gamma }{\beta }\) the proportion of infected reaches the maximum value. Therefore, one way to consider control in the SIR model is to change the contact rate \( \beta \), where the lower the value of \(\beta \), the greater the proportion of susceptible people \( S ^ * \) (who were not infected) at peak \( I (S ^ *) \). It is worth noting that the peak \( I (S^*) \) depends on the value of the constant k according to (23) (see Fig. 8).

It is reasonable to consider that, in the relaxation phase in control, the contact rate is higher than the one in the phase with social isolation. Consequently, we have a value of \( S_1 ^ * \) for the phase with isolation and a value of \( S_2 ^ * \) for the phase after relaxation. In this case, we have the following peaks: \(I(S_1^*)\) and \(I(S_2^*)\).

Fig. 8
figure 8

Phase plane \(S\times I\) of the SIR model. The black dashed curve represents a scenario without control measures. The red and blue dashed curves are given by Eq. (23) for some value of k. \(\overline{S}_1\) represents the proportion of susceptible people at the moment when the first social isolation begins. \(\overline{S}_2\) represents the the proportion of susceptible people at the moment when control measures are relaxed. The evolution of the epidemic with control through social isolation is given by the green curve

Full size image

Figure 8 suggests that each plateau (i.e. stabilization at a low level of infected individuals) occurs between the first and second waves. Therefore, in this case, the plateau occurs when the proportion of susceptible individuals is around \(\overline{S}_2\).

6 Discussion and conclusions

In this work we have verified, under statistic point of view, the memory effect in the fractional calculus. We have shown that both fractional integral and derivative of a function f in instant t are, respectively, proportional to average of f(s) of the function and its classical derivative \(f'(s)\), for all instants s between zero and t. So, in fact, the fractional calculus is an appropriate methodology to treat dynamical systems with memory. From this approach we also proved the loss of the memory effect when \( \alpha = 1 \) in (11)–(13), that is, when we return to the classic case. Moreover, since memory effect can involve the entire history before the present instant, that is, it considers all times s from 0 to t, fractional calculus can be viewed as a suitable tool for modeling of phenomenon with hysteresis. The hysteresis phenomenon can be seen in several dynamic systems, such as physical or biological systems, for which important properties depend on its entire past history.

In addition, we show that the contribution of the function values to the fractional operators is higher or lower according to the order of the operator. In particular, the final values of the function have greater influence on the values of the fractional Riemann–Liouville and Caputo derivatives for \(0<\alpha <1\).

We illustrate the use of a fractional model to model a system with memory using a simple compartmental SIR model which is a well-known and applicable model in epidemiology. Specifically, we study COVID-19 by assuming that it obeys the dynamics of the SIR epidemiologic model. For the purpose of comparing the results obtained via fractional calculus and via classical calculus, we study the evolution of COVID-19 in four countries, namely South Korea, China, Switzerland and, Italy. The results for these countries show that the fractional calculus produced more satisfactory results than those obtained using the classical theory. We also have studied the control of the epidemic through policies of social isolation.