Effects of the crack location on the dynamic response of multi-storey frame subjected to the passage of a high-speed train

Abstract

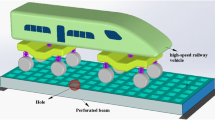
The high-speed railways require more viaduct than a conventional railway. When the viaduct is subjected to high-amplitude vibrations for a long time, the fatigue-induced crack formation can occur . The presence of a crack changes the stiffness of the structure. Depending on the location of the crack, the reduction effect in stiffness varies. In this study, the presence of a single crack in a multi-storey frame structure, which is considered as a viaduct model, has been investigated. Effects of crack location on the dynamic response are investigated via 3D velocity-crack location-dynamic magnification factor (or maximum displacement) graphs. The train is modelled as a four-axle two-bogie multi-body system with 10 DOF and moving at a constant speed. The finite element method, based on Euler–Bernoulli beam theory, is used to simulate the vibrations of the coupled vehicle-structure system. Wilson-theta time integration scheme is used to solve the equation of motion. It has been determined that when the crack is located at the midpoint of the top beam, the highest effect on the dynamic response is observed.

Appdendix

In Eq. (13), the following abbreviations have been introduced:

$$\begin{aligned} \varvec{M}_{fv}^i<q_1^{ei}>= & {} \begin{bmatrix} 0 . . m_w N_1^2 0 0 m_w N_1 N_4 0 0 . . 0 \end{bmatrix}^T \nonumber \\ \varvec{M}_{fv}^i<q_4^{ei}>= & {} \begin{bmatrix} 0 . . m_w N_1 N_4 0 0 m_w N_1^2 0 0 . . 0 \end{bmatrix}^T \end{aligned}$$

(17)

$$\begin{aligned} \varvec{C}_{fv}^i<q_1^{ei}>= & {} \begin{bmatrix} 0 \\ . \\ . \\ 2 V m_w N_1 N_{1,x} + c_p N_1^2 \\ 0 \\ 0 \\ 2 V m_w N_{1,x} N_4 + c_p N_1 N_4 \\ 0\\ 0 \\ . \\ . \\ 0 \end{bmatrix}\,, \quad \varvec{C}_{fv}^i<q_4^{ei}> = \begin{bmatrix} 0 \\ . \\ . \\ 2 V m_w N_1 N_{4,x} + c_p N_1 N_4 \\ 0 \\ 0 \\ 2 V m_w N_4 N_{4,x} + c_p N_4^2 \\ 0\\ 0 \\ . \\ . \\ 0 \end{bmatrix} \end{aligned}$$

(18)

$$\begin{aligned} \varvec{K}_{fv}^i<q_1^{ei}>= & {} \begin{bmatrix} 0 \\ . \\ . \\ m_w V^2 N_1 N_{1,xx} + c_p V N_1 N_{1,x} + k_p N_1^2 \\ 0 \\ 0 \\ m_w V^2 N_1 N_{4,xx} + c_p V N_1 N_{4,x} + k_p N_1 N_4 \\ 0\\ 0 \\ . \\ . \\ 0 \end{bmatrix}\,, \nonumber \\ \varvec{K}_{fv}^i<q_4^{ei}>= & {} \begin{bmatrix} 0 \\ . \\ . \\ m_w V^2 N_{1,xx} N_4 + c_p V N_{1,x} N_4 + k_p N_1 N_4 \\ 0 \\ 0 \\ m_w V^2 N_4 N_{4,xx} + c_p V N_4 N_{4,x} + k_p N_4^2 \\ 0\\ 0 \\ . \\ . \\ 0 \end{bmatrix} \end{aligned}$$

(19)

where $i=1,2,3,4$.

$$\begin{aligned}&\varvec{\bar{A}}_{vf} = \begin{bmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} - a_p N_1&{} 0 &{} 0 &{} a_p L_b N_1 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} - a_p N_4 &{} 0 &{}0 &{} a_p L_b N_4 &{} 0\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ 0 &{} - a_p N_1&{} 0 &{} 0 &{} -a_p L_b N_1 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} - a_p N_4 &{} 0 &{} 0 &{} -a_p L_b N_4 &{} 0\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ - a_p N_1&{} 0 &{} 0 &{} a_p L_b N_1 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ - a_p N_4 &{} 0 &{} 0 &{} a_p L_b N_4 &{} 0 &{} 0\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ - a_p N_1&{} 0 &{} 0 &{} -a_p L_b N_1 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ - a_p N_4 &{} 0 &{} 0 &{} -a_p L_b N_4 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ \end{bmatrix} \end{aligned}$$

(20)

$$\begin{aligned}&\quad \varvec{M}_{v} = diag(m_b, m_b, m_{v}, J_b, J_b, J_{v}) \end{aligned}$$

(21)

$$\begin{aligned}&\quad \varvec{A}_v = \begin{bmatrix} 2 a_p + a_s &{} 0 &{} -a_s &{} 0 &{} 0 &{} -d_1 a_s\\ 0 &{} 2 a_p + a_s &{} -a_s &{} 0 &{} 0 &{} d_2 c_s\\ -a_s &{} -a_s &{} 2 a_s 0 &{} 0 &{} (d_1-d_2)a_s\\ 0 &{} 0 &{} 0 &{} 2 L_b^2 a_p &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 2 L_b^2 a_p &{} 0 \\ -d_1 a_s &{} d_2 a_s &{} (d_1-d_2)a_s &{} 0 &{} 0 &{} (d_1^2+d_2^2)a_s \end{bmatrix} \end{aligned}$$

(22)

Notation $\varvec{A}<q_j^{ei}>$ represents the $j{\rm th}$ column of the element ei in the matrix $\varvec{A}$. If $\varvec{A}$ and a in matrices $\varvec{\bar{A}}_{vf}$ and $\varvec{A}_{v}$ in Eqs. (20) and (22) are replaced by $\varvec{C}$ and c (or $\varvec{K}$ and k), matrices $\varvec{\bar{C}}_{vf}$ and $\varvec{C}_v$ (or matrices $\varvec{\bar{K}}_{vf}$ and $\varvec{K}_v$) can be determined.