Skip to main content
SpringerLink
Log in

New positional accuracy calibration method for an autonomous robotic inspection system

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

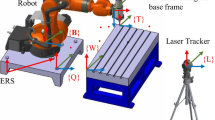
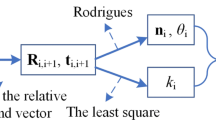
The existing automatic inspection system employed for the quality assessment in the manufacturing of automotive parts, comprising industrial robots and sensors, has a low absolute positioning accuracy. Therefore, a new method based on an optimally pruned extreme learning machine algorithm is proposed to compensate for the absolute positional errors. This algorithm is applied to the positional error compensation of a robot end-effector by mapping the robot target position to the computed position. We selected sampling points in the robot motion space to establish an error prediction model and used the trained model to predict the error at the test points. Experiments were carried out to verify the effectiveness of the proposed method in measuring the robot positional errors in the x, y, and z axes and the total absolute accuracy. The maximum absolute positional error reduced by 78.3% from 1.472 to 0.319 mm, and the average positional error reduced by 84.5% from 1.235 to 0.191 mm. A robot was made to move along a predetermined trajectory at different speeds with improved positioning accuracy. A comparison experiment was performed to validate the accuracy and superiority of the method. The experimental results showed that the proposed method could significantly improve the positional accuracy of the robotic inspection system and that the method represents an effective and convenient technique for robot calibration in workshops.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Chen Y, Dong F (2013) Robot machining: recent development and future research issues. The Int J Adv Manuf Technol 66(9–12):1489–1497

    Article  Google Scholar 

  2. Guo Y, Yin S, Ren Y et al (2015) A multilevel calibration technique for an industrial robot with parallelogram mechanism. Precis Eng 40:261–272

    Article  Google Scholar 

  3. Summers M (2005) Robot capability test and development of industrial robot positioning system for the aerospace industry. SAE Tran 114(1):1108–1118

    MathSciNet  Google Scholar 

  4. Gang Chen, Tong Li, Ming Chu et al (2014) Review on kinematics calibration technology of serial robots. Int J Precis Eng Manuf 15(8):1759–1774

    Article  Google Scholar 

  5. Liu Z, Zhao ZD, Xie Y et al (2015) Kinematic calibration and compensation for a robot with structural deformation. Robot 37(3):376–384

    Google Scholar 

  6. Denavit J, Hartenberg RS (1955) A kinematic notation for lower-pair mechanisms based on matrices. J Appl Mech 22:215–221

    Article  MathSciNet  Google Scholar 

  7. Gatti G, Danieli G (2007) A practical approach to compensate for geometric errors in measuring arms: application to a six-degree-of-freedom kinematic structure. Meas Sci Technol 19(1):1–12

    Google Scholar 

  8. Stone HW, Sanderson AC (1988) Statistical performance evaluation of the S-model arm signature identification technique. IEEE International Conference on Robotics and Automation, pp 939–946

  9. Rosvold JM, Atarod M, Frank CB et al (2015) An instrumented spatial linkage for measuring knee joint kinematics[J]. Knee 23(1):43–48

    Article  Google Scholar 

  10. Li C, Yuanqing W, Lowe H et al (2016) POE-based robot kinematic calibration using axis configuration space and the adjoint error model [J]. IEEE Trans Robot 32(5):1264–1279

    Article  Google Scholar 

  11. Zak G, Benhabib B, Fenton R, Saban I (1994) Application of the weighted least squares parameter estimation method to the robot calibration. J Mech Des 116(3):890–893

    Article  Google Scholar 

  12. Motta JMST (2001) Robot calibration using a 3D vision-based measurement system with a single camera. Robot Comput Integrat Manuf 17(6):487–497

    Article  Google Scholar 

  13. Nubiola A, Bonev I (2013) Absolute calibration of an ABB IRB 1600 robot using a laser tracker. Robot Comput Integr Manuf 29(1):236–245

    Article  Google Scholar 

  14. Nguyen H, Zhou J, Kang H (2015) A calibration method for enhancing robot accuracy through integration of an extended Kalman filter algorithm and an artificial neural network. Neurocomputing 151(P3):996–1005

    Article  Google Scholar 

  15. Render JM, Rossignal E, Becquet M, Hanus R (1991) Kinematic calibration and geometrical parameter identification for robots. IEEE Trans Robot Autom 7(6):721–732

    Article  Google Scholar 

  16. Omodei A, Legnani G, Adamini R (2000) Three methodologies for the calibration of industrial manipulators: experimental results on a SCARA robots. J Robot Syst 17(6):291–307

    Article  Google Scholar 

  17. Bai Y (2007) On the comparison of model-based and modeless robotic calibration based on a fuzzy interpolation method. Int J Adv Manuf Technol 31(11–12):1243–1250

    Article  Google Scholar 

  18. Alici G, Shirinzadeh B (2005) A systematic technique to estimate positioning errors for robot accuracy improvement using laser interferometry based sensing. Mech Mach Theory 40:879–906

    Article  Google Scholar 

  19. Zhou W, Liao W, Tian W (2013) Theory and experiment of industrial robot accuracy compensation method based on Spatial Interpolation. J Mech Eng 49(3):42–48

    Article  Google Scholar 

  20. Cai Y, Yuan P, Shi Z (2019) Application of Universal Kriging for Calibrating offline-programming Industrial Robots. J Intell Rob Syst 94:339–348

    Article  Google Scholar 

  21. Chen D, Yuan P et al (2018) A compensation method for enhancing aviation drilling robot accuracy based on Co-Kriging. Int J Precis Eng Manuf 19(8):1133–1142

    Article  Google Scholar 

  22. Rui MA, Yushu L, Yanhui D (2004) An intrusion detection method based on neural network expert system. Comput Eng Appl 40:151–153

    Google Scholar 

  23. Yuan P, Chen D, Wang T et al (2018) A compensation method based on extreme learning machine to enhance absolute position accuracy for aviation drilling robot. Adv Mech Eng 10(3):1–11

    Article  Google Scholar 

  24. Longfei W, Xu L, Liyan Z et al (2018) Analysis of the Positioning error of Industrial robots and accuracy compensation based on ELM algorithm. ROBOT 40(6):843–851

    Google Scholar 

  25. Efron B, Hastie T, Johnstone I, Tibshirani R (2004) Least angle regression. Statist 32(2):407–499

    Article  MathSciNet  Google Scholar 

  26. Boyd S, Vandenberghe L (2004) Convex optimization[M]. Cambridge University Press, New York, USA

    Book  Google Scholar 

  27. Huang GB, Zhu QY, Siew CK (2006) Extreme learning machine: Theory and applications. Neurocomputing 70:489–501

    Article  Google Scholar 

Download references

Acknowledgements

This research was sponsored by the National Key Research and Development Project [No. 2018YFB1701002] and Research and Development plan for key areas in Guangdong Province [No. 2019B090919001].

Author information

Authors and Affiliations

  1. National Number Control System Engineering Research Center, School of Mechanical Science and Engineering, Huazhong University of Science and Technology, 1037 Luoyu Road, Wuhan, 430074, China

    Geng Chen, Jianzhong Yang, Hua Xiang & Daojiang Ou

  2. Xiangyang Huazhong University of Science and Technology Advanced Manufacturing Engineering Research Institute, Ring Road, Dongjin New District, XiangYang, 441002, China

    Geng Chen

Authors
  1. Geng Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jianzhong Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hua Xiang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Daojiang Ou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hua Xiang.

Additional information

Technical Editor: Rogério Sales Gonçalves.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chen, G., Yang, J., Xiang, H. et al. New positional accuracy calibration method for an autonomous robotic inspection system. J Braz. Soc. Mech. Sci. Eng. 44, 177 (2022). https://doi.org/10.1007/s40430-022-03487-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-022-03487-x

Keywords

Search

Navigation