1 Introduction

The stochastic averaging method was proposed initially by Stratonovich [1] to deal with weakly nonlinear systems subjected to stationary broad-band random excitations. Two approximation procedures are carried out in the method: one is the replacement of the broad-band processes by Gaussian white noises, and another is the time averaging to eliminate the fast varying processes and reduce the system dimension. The remaining slowly varying processes are then approximated as a Markov vector process with its probability density governed by the Fokker–Planck equation. The validity of the stochastic averaging method was established rigorous by Khasminskii [2] and Papanicolaou and Kohler [3], and also by Lin [4] from a different perspective with clearer physical implication and more appealing to engineers. The method has been proved to be a useful tool in the stochastic dynamics. Reviews of the method and its applications were given by Roberts and Spanos [5], Zhu [6, 7], and Lin and Cai [8].

The original version of the stochastic averaging method is applied to a system with linear stiffness, weakly nonlinear damping, and weak broad-band random excitations. The system is governed by

$$\begin{aligned} \ddot{X} + \varepsilon h ( X , \dot{X} ) + \omega _0^2 X = \varepsilon ^{1 / 2} \sum _{i=1}^{n} g_i ( X , \dot{X} ) \xi _i ( t ) \end{aligned}$$
(1)

where \(\varepsilon \) is a small parameter, \(h(X,\dot{X})\) is the damping force, and \(\xi _{i}(t)\) are random excitations of broad bandwidth. The slowly varying system response is the amplitude process. Another version of the stochastic averaging, named as the quasi-conservative averaging [9, 10], or the stochastic averaging of energy envelop [11], is applicable to a system with a strongly nonlinear stiffness force. The method was originally dealing with the system

$$\begin{aligned} \ddot{X} + \varepsilon h ( X , \dot{X} ) + u ( X ) = \varepsilon ^{1 / 2}\sum _{i=1}^{n} g_i ( X , \dot{X} ) W_i ( t ) \end{aligned}$$
(2)

where \(u(X)\) is a strongly nonlinear restoring force, and \(W_{i}(t)\) are Gaussian white noises. For system (2), the slowly varying process is the energy process. Since the excitations are white noises, only the time averaging is needed. Several schemes were proposed to extend the method to non-white broad-band excitations, including the Fourier-expansion [12, 13], the energy-dependent white-noise approximation [14], the residual phase procedure [15], and the generalized harmonic function [16]. Applications also included the combination of harmonic and white noise excitations [17], the bounded noise excitations [18], and multi-degree-of freedom quasi Hamiltonian systems [19].

The strongly nonlinear restoring force \(u(X)\) considered in the above quasi-conservative averaging scheme is a monotonic function, namely, its corresponding potential energy has a single-well shape. If the potential has a double-well shape and the restoring force is not monotonic, then the system motion is more complicated. It may moves in one well, transit from one well to another, or move all over two wells. Thus, the above developed schemes of the quasi-conservative averaging are no longer applicable. For investigating such type of systems, a procedure is proposed in the present paper to extend the application of the quasi-conservative averaging. Both external and parametric excitations of wide-band random processes are considered. The asymptotic behaviors of the response at boundaries, the stationary response of the system, and the transition between two wells are investigated. Monte Carlo simulations are carried out to substantiate the proposed procedure.

2 Deterministic conservative system

A typical conservative dynamical system with a double-well potential is given by

$$\begin{aligned} \ddot{x}-\alpha x+\beta x^{3}=0 \end{aligned}$$
(3)

where \(\alpha \) and \(\beta \) are two positive constants. The potential energy and total energy of the system are, respectively,

$$\begin{aligned}&U(x)=-\frac{1}{2}\alpha x^{2}+\frac{1}{4}\beta x^{4}+\frac{\alpha ^{2}}{4\beta }\end{aligned}$$
(4)
$$\begin{aligned}&\lambda (x,\dot{x})=\frac{1}{2}\dot{x}^{2}-\frac{1}{2}\alpha x^{2}+\frac{1}{4}\beta x^{4}+\frac{\alpha ^{2}}{4\beta } \end{aligned}$$
(5)

where the constant \(\alpha ^{2}/(4\beta )\) is added so that both the potential energy and total energy are nonnegative. Figure 1 shows the double-well potential energy of the system schematically.

Fig. 1
figure 1

Double-well potential energy of system (3)

Full size image

Letting \(x_{1}=x\) and \(x_2 =\dot{x}\), system (3) can be written in the state space as follows

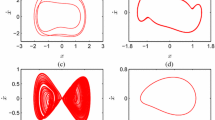
$$\begin{aligned} \begin{array}{l} \dot{x}_1 =x_2 \\ \dot{x}_2 =\alpha x_1 -\beta x_1^3 \\ \end{array} \end{aligned}$$
(6)

The system has three equilibriums at (0, 0),\((-\sqrt{\alpha /\beta }, 0)\), and \((\sqrt{\alpha /\beta }, 0)\). For initial conditions other than at these three points, the system motion is periodic. Depending on the initial condition, the periodic motion may be in one of the potential wells, or pass through both wells. Figure 2 shows these periodic motions schematically. If the total energy is less than \(\alpha ^{2}/ (4\beta )\), there are two possible motions, located on either side of the phase plane. For a given initial state of (\(x_{10}, x_{20}\)) in this case, the periodic trajectory is restricted on one side of the phase plane depending on the sign of \(x_{10}\). The lower of the total energy is, the closer of the trajectory is to one of the stable equilibriums. When the total energy exceeds \(\alpha ^{2}/ (4\beta )\), the system moves across the entire phase plane, and only one periodic trajectory corresponds to a given energy level. It is noted that (i) the periodic motion in either case is far from harmonic except for a very low energy level, (ii) the concept of amplitude is no longer meaningful in the case of \(\lambda \, <\,\alpha ^{2}/(4\beta )\).

Fig. 2
figure 2

Periodic motions of system (3) corresponding to different energy levels

Full size image

For a given energy level \(\lambda \, <\,\alpha ^{2}/(4\beta )\), the natural period of the motion can be calculated from

$$\begin{aligned} T(\lambda )=\oint {{\text{ d}}t=\oint {\frac{{\text{ d}}x}{\dot{x}}=2\int \limits _{x_a}^{x_b} {\frac{{\text{ d}}x}{\sqrt{2\lambda -\frac{\alpha ^{2}}{2\beta }+\alpha x^{2}-\frac{\beta }{2}x^{4}}}}}} \nonumber \\ \end{aligned}$$
(7)

where \(x_{a}\) and \(x_{b}\) are the smallest and largest values of \(x\) respectively, calculated from

$$\begin{aligned} x_a =\sqrt{\frac{1}{\beta }(\alpha -\sqrt{4\beta \lambda })},\quad x_b =\sqrt{\frac{1}{\beta }(\alpha +\sqrt{4\beta \lambda })} \end{aligned}$$
(8)

In deriving (7), it is assumed that the motion is on the right side of the phase plane, i.e., \(x\) is always positive. Due to the symmetry, the period is the same if the motion is on the other side. Neither \(x_{a}\) nor \(x_{b}\) has the meaning of amplitude in this case.

If the energy level \(\lambda \, >\,\alpha ^{2}/(4\beta )\), the natural period is obtained from

$$\begin{aligned} T(\lambda )=\oint {{\text{ d}}t=\oint {\frac{{\text{ d}}x}{\dot{x}}=4\int \limits _0^{x_b } {\frac{{\text{ d}}x}{\sqrt{2\lambda -\frac{\alpha ^{2}}{2\beta }+\alpha x^{2}-\frac{\beta }{2}x^{4}}}}}} \nonumber \\ \end{aligned}$$
(9)

where \(x_{b}\) is also given in (8), known as the amplitude of the periodic motion in the case. Figure 3 shows the natural period and circular frequency (\(\omega = 2\pi /T\)) versus the energy level for the case of \(\alpha = 2\) and \(\beta =1\). At \(\lambda = \alpha ^{2}/ (4\beta ) = 1\), the period has a jump of twice value. This is because the motion jumps from a small trajectory on one side of the phase plane to a twice large trajectory on the entire plane. When \(\lambda \, <\, \alpha ^{2}/(4\beta ) = 1\), the term \(-\alpha x\) plays the dominant role, the system stiffness decreases with an increasing energy level, leading to an increasing period and decreasing frequency. In the energy level of 0 \(< \, \lambda \, <1\), the natural frequency is in the range of 1 \(< \, \omega < \,2\). On the other hand, when \(\lambda \, >\,\alpha ^{2}/ (4\beta ) = 1\), the term \(\beta x^{3}\) is dominant, indicating a hardening stiffness. Thus, the larger the energy level, the larger the natural frequency is and the shorter the period is. However, the natural frequency remains in the range of \(1 < \, \omega < \, 2\) even up to quite high energy level of \(\lambda =12\). Figure 3 also shows that the behavior of the system natural frequency and period is very much different from those of a system with a single potential well.

Fig. 3
figure 3

Natural period and frequency of system (3) with respect to energy level \(\lambda \)

Full size image

For the limiting case of \(\lambda \rightarrow 0, x\) approaches either \(\sqrt{\alpha /\beta }\) or \(-\sqrt{\alpha /\beta }\). Without loss of generality, assume that it approaches \(\sqrt{\alpha /\beta }\). Denoting

$$\begin{aligned} x_e =x-\sqrt{\frac{\alpha }{\beta }} \end{aligned}$$
(10)

and neglecting higher-order terms, we have

$$\begin{aligned} \ddot{x}_e +2\alpha x_e =0 \end{aligned}$$
(11)

Equation (11) indicates that the system can be approximated as a linear oscillator around the equilibrium point \((\sqrt{\alpha /\beta },0)\), and with a limiting period,

$$\begin{aligned} \mathop {\lim }\limits _{\lambda \rightarrow 0}\, T=\frac{\sqrt{2}\pi }{\sqrt{\alpha }} \end{aligned}$$
(12)

3 Stochastic system analysis

Consider the following stochastic system with a double-well potential

$$\begin{aligned} \ddot{X} + \varepsilon h ( X , \dot{X} ) - \alpha X + \beta X^3 = \varepsilon ^{1 / 2} \sum _{i=1}^{n}g_i ( X , \dot{X} ) \xi _i ( t ) \nonumber \\ \end{aligned}$$
(13)

where \(h ( X , \dot{X} )\) represents a damping force, \(\xi _{i}(t)\) are non-white random excitations, and \(\varepsilon \) is a small parameter. Equation (11) indicates that damping is of the order of \(\varepsilon \), and excitations are of order of \(\varepsilon ^{1/2}\). For the present investigation, we assume that \(\xi _{i}(t)\) are stationary random processes with zero means and the following correlation functions

$$\begin{aligned} R_{ij} (\tau )=E[\xi _i (t)\xi _j (t+\tau )] \end{aligned}$$
(14)

3.1 Stochastic averaging

The total energy of system (13) is also a stochastic process, defined as

$$\begin{aligned} \Lambda (t)=\Lambda (X,\dot{X})=\frac{1}{2}\dot{X}^{2}-\frac{1}{2}\alpha X^{2}+\frac{1}{4}\beta X^{4}+\frac{\alpha ^{2}}{4\beta } \end{aligned}$$
(15)

which is the stochastic counterpart of \(\lambda (x,\dot{x})\) defined in (5). In terms of \(X (t)\) and \(\Lambda (t)\), the system equation of motion, Eq. (13), can be replaced by a set of two first-order equations

$$\begin{aligned} \dot{X}&= \pm \sqrt{2\Lambda - \frac{{\alpha ^{2} }}{{2\beta }} + \alpha X^{2} - \frac{1}{2}\beta X^{4} } \nonumber \\ \dot{\Lambda }&= - \varepsilon \dot{X} h ( X , \dot{X} ) + \varepsilon ^{1 / 2} \sum _{i=1}^{n} \dot{X} g_{i} (X, \dot{X})\xi _{i} ( t ) \end{aligned}$$
(16)

where \(\dot{X}\) in the second equation is treated as a function of \(X\) and \(\Lambda \) according to (15). The second equation in (16) shows that the energy process \(\Lambda (t)\) is slowly varying when the damping and the excitation are small. If, in addition, the correlation times of the excitations \(\xi _{i }(t)\) are short compared with the relaxation time of the system [8], then the \(\Lambda (t)\) process is approximately Markovian, governed by an Itô stochastic differential equation [20]

$$\begin{aligned} {\text{ d}} \Lambda = m (\Lambda ) + \sigma (\Lambda ) d B ( t ) \end{aligned}$$
(17)

where \(B(t)\) is a unit Wiener process, \(m(\Lambda )\) and \(\sigma (\Lambda )\) are known as the drift and diffusion coefficients, respectively. They can be calculated from [8]

$$\begin{aligned} m(\Lambda )&= -\varepsilon \left\langle {\dot{X}h(X,\dot{X})} \right\rangle _t\nonumber \\&+\varepsilon \int \limits _{-\infty }^0 \sum _{i=1}^n {\sum _{j=1}^n {\left\langle {\dot{X}(t{+}\tau )g_j (t{+}\tau )\frac{\partial }{\partial \Lambda }[\dot{X}(t)g_i (t)]} \right\rangle _t } }\nonumber \\&\times R_{ij} (\tau ) {\text{ d}}\tau \end{aligned}$$
(18)
$$\begin{aligned} \sigma ^{2}(\Lambda )&= \varepsilon \int \limits _{-\infty }^\infty \sum _{i=1}^n {\sum _{j=1}^n {\left\langle {\dot{X}(t)g_j (t)\dot{X}(t+\tau )g_i (t+\tau )} \right\rangle _t } }\nonumber \\&\times R_{ij} (\tau ){\text{ d}}\tau \end{aligned}$$
(19)

where \(\left\langle {[\cdot ]} \right\rangle _t \) denotes the time average over one quasi-period, defined as

$$\begin{aligned} \left\langle {[\cdot ]} \right\rangle _t =\frac{1}{T}\oint {\left[ \cdot \right] \,{\text{ d}}t=\frac{1}{T}\oint {\frac{\left[ \cdot \right] {}{\text{ d}}X}{\dot{X}}} } \end{aligned}$$
(20)

The closed-loop integration in (20) is carried out along the periodic trajectories of system (3), corresponding to different energy levels shown in Fig. 2. Since the different natures of the periodic trajectories for the two different cases of \(\Lambda < \alpha ^{2}/ (4\beta )\) and \(\Lambda >\alpha ^{2}/ (4\beta )\), the time averaging procedure needs also to be carried out differently for the two cases. The result obtained from each time average in (18) and (19) is a function of \(\Lambda \) and \(\tau \). With correlation functions \(R_{ij }(\tau )\) given, \(m (\Lambda )\) and \(\sigma (\Lambda )\) can be calculated numerically. Equations (17), (18), and (19) constitute the governing law for the one dimensional Markov process \(\Lambda (\text{ t})\).

If the excitations are Gaussian white noises, \(R_{ij} (\tau )=2\pi K_{ij} \delta (\tau )\), where \(K_{ij}\) are the spectral densities of the white noises, (18) and (19) reduce to

$$\begin{aligned} m(\Lambda )&= -\varepsilon \left\langle {\dot{X}h(X,\dot{X})} \right\rangle _t \nonumber \\&\quad +\varepsilon \pi \sum _{i=1}^n {\sum _{j=1}^n {K_{ij} \left\langle {\dot{X}(t)g_j (t)\frac{\partial }{\partial \Lambda }[\dot{X}(t)g_i (t)]} \right\rangle _t } } \nonumber \\ \end{aligned}$$
(21)
$$\begin{aligned} \sigma ^{2}(\Lambda )&= \varepsilon 2\pi \sum _{i=1}^n {\sum _{j=1}^n {K_{ij} \left\langle {\dot{X}^{2}(t)g_j (t)g_i (t)} \right\rangle _t } } \end{aligned}$$
(22)

Calculation of (21) and (22) are relatively straightforward.

3.2 Asymptotic behaviors

The qualitative behavior of the one dimensional Markov Diffusion process \(\Lambda (\text{ t})\) depends on the sample behaviors of the process at the two boundaries at \(\Lambda = 0\) and \(\Lambda =\infty \). Based on the asymptotic behaviors of the drift and diffusion coefficients, the two boundaries can be classified into different categories [8]. Systems with different types of damping \(h(X,\dot{X})\)and different types of excitations on the right side of Eq. (13) will have different natures of the two boundaries. Three scenarios are possible: (i) the equilibrium point (0, 0) is asymptotically stable, (ii) a non-trivial stationary probability distribution exists, and (iii) the system is divergent. The example in the paper will illustrate how to identify the boundaries.

3.3 Stationary probability density functions

When each of the two boundaries is either an entrances or repulsively natural, a non-trivial stationary probability distribution exists [8]. It can be obtained from the Itô equation (17) as

$$\begin{aligned} p(\lambda )=\frac{C}{\sigma ^{2}(\lambda )}\exp \left[ {\int {\frac{2m(\lambda )}{\sigma ^{2}(\lambda )}{\text{ d}}\lambda } } \right] \end{aligned}$$
(23)

where \(\lambda \) is the state variable of \(\Lambda (t)\), and \(C\) is a normalization constant.

The joint probability density of \(\Lambda (t)\) and \(X (t), p (\lambda , x)\), can be written as

$$\begin{aligned} p(\lambda ,x)=p(x|\lambda )p(\lambda ) \end{aligned}$$
(24)

where \(p(x|\lambda )\) is the conditional probability density of \(X(t)\) given \(\Lambda (t)=\lambda \). It can be obtained as follows

$$\begin{aligned} p(x|\lambda )\text{ d}x=\frac{{\text{ d}}t}{T(\lambda )}=\frac{{\text{ d}}x}{\left| {\dot{x}} \right| T(\lambda )} \end{aligned}$$
(25)

Substitution of (25) into (24) leads to

$$\begin{aligned} p(\lambda ,x)=\frac{p(\lambda )}{\left| {\dot{x}} \right| T(\lambda )} \end{aligned}$$
(26)

in which \(\dot{x}\) is treated as a function of \(x\) and \(\lambda \). Thus, the joint probability density \(p(x,\dot{x})\) follows as

$$\begin{aligned} p(x,\dot{x})=p(\lambda ,x)\left| {\begin{array}{l} \frac{\partial \lambda }{\partial x}\;\frac{\partial \lambda }{\partial \dot{x}} \\ \frac{\partial x}{\partial x}\;\;\frac{\partial x}{\partial \dot{x}} \\ \end{array}} \right| =p(\lambda ,x)\left| {\dot{x}} \right| =\frac{p(\lambda )}{T(\lambda )} \end{aligned}$$
(27)

The marginal probability densities of \(X\) and \(\dot{X}\) can then be obtained as

$$\begin{aligned} p(x)=\int \limits _{-\infty }^\infty {p(x,\dot{x})} {\text{ d}}\dot{x},\quad p(\dot{x})=\int \limits _{-\infty }^\infty {p(x,\dot{x})} {\text{ d}}x \end{aligned}$$
(28)

Consider a special case of a linear damping and an external white-noise excitation, i.e.,

$$\begin{aligned} \ddot{X} + \gamma (\dot{X} )-\alpha X +\beta X^3=W(t) \end{aligned}$$
(29)

We have from (21) and (22)

$$\begin{aligned} m(\Lambda )&= -\gamma \left\langle {\dot{X}^{2}} \right\rangle _t +\pi K \end{aligned}$$
(30)
$$\begin{aligned} \sigma ^{2}(\Lambda )&= 2\pi K\left\langle {\dot{X}^{2}} \right\rangle _t \end{aligned}$$
(31)

where \(K\) is the power spectral density of \(W(t)\). Substituting (30) and (31) into (23), we obtain

$$\begin{aligned} p(\lambda )=\frac{C}{\left\langle {\dot{x}^{2}} \right\rangle _t }\exp \left( {\int {\frac{{\text{ d}}\lambda }{\left\langle {\dot{x}^{2}} \right\rangle _t }} } \right) \exp \left( {-\frac{\gamma }{\pi K}\lambda } \right) \end{aligned}$$
(32)

It can be proved that

$$\begin{aligned} \frac{{\text{ d}}}{{\text{ d}}\lambda }\ln \left[ {T(\lambda )\left\langle {\dot{x}^{2}} \right\rangle _t } \right] =\frac{1}{\left\langle {\dot{x}^{2}} \right\rangle _t } \end{aligned}$$
(33)

Using (33), (32) is simplified to

$$\begin{aligned} p(\lambda )=CT(\lambda )\exp \left( {-\frac{\gamma }{\pi K}\lambda } \right) \end{aligned}$$
(34)

The stationary probability density \(p(x,\dot{x})\) can then be derived from (27)

$$\begin{aligned} p(x,\dot{x})&= C\exp \left( {-\frac{\gamma }{\pi K}\lambda } \right) \nonumber \\&= C_1 \exp \left[ {-\frac{\gamma }{2\pi K}\left( {-\alpha x^{2}+\frac{1}{2}\beta x^{4}+\dot{x}^{2}} \right) } \right] \end{aligned}$$
(35)

which is in fact the exact stationary probability density.

3.4 Transition between two wells

Assume that the system is in one well initially. After the random excitations are applied, it begins to oscillate randomly in the well. When the energy exceeds the critical value \(\lambda _c =\alpha ^{2}/(4\beta )\), it will jump into another well. The average transition time beginning from an initial energy level \(\lambda _{0}\), denoted by \(\mu (\lambda _{0})\), is governed by the well-known Pontryagin equation [21]

$$\begin{aligned} 1+m(\lambda _0 )\frac{{\text{ d}}\mu }{{\text{ d}}\lambda { }_0}+\frac{1}{2}\sigma ^{2}(\lambda _0 )\frac{{\text{ d}}^{2}\mu }{{\text{ d}}\lambda _0^2 }=0 \end{aligned}$$
(36)

where \(m(\lambda _{0})\) and \(\sigma (\lambda _{0})\) are given by Eqs. (18) and (19) with \(\Lambda \) replaced by \(\lambda _{0}\). The boundary conditions for Eq. (36) are

$$\begin{aligned} \mu (\lambda _c )=0,\quad \left. {\frac{{\text{ d}}\mu }{{\text{ d}}\lambda _0 }} \right| _{\lambda _0 =0} =-\frac{1}{m(0)} \end{aligned}$$
(37)

The second condition can be derived directly from Eq. (36) since it can be shown that \(\sigma ^{2}(0) = 0\). The solution of (36) satisfying the two boundary conditions are derived as

$$\begin{aligned} \mu (\lambda _0 )&= -\int \limits _{\lambda _0 }^{\lambda _c } {f(z){\text{ d}}z} \end{aligned}$$
(38)
$$\begin{aligned} f(z)&= \exp \left[ {-\int \limits _0^z {\frac{2m(u)}{\sigma ^{2}(u)}{\text{ d}}u} } \right] \nonumber \\&\times \left\{ {-\int \limits _0^z {\frac{2}{\sigma ^{2}(u)}} \exp \left[ {\int \limits _0^u {\frac{2m(v)}{\sigma ^{2}(v)}{\text{ d}}v} } \right] {\text{ d}}u-\frac{1}{m(0)}} \right\} \nonumber \\ \end{aligned}$$
(39)

The average transition time can be calculated numerically from (38) and (39).

4 An example

As an example, consider the following oscillator

$$\begin{aligned} \ddot{X}+\gamma \dot{X}-\alpha X+\beta X^{3}=X\xi _1 (t)+\xi _2(t) \end{aligned}$$
(40)

where the damping force is assumed to be of order \(\varepsilon \), and \(\xi _{1}(t)\) and \(\xi _{2}(t)\) are independent stationary broad-band random processes of order \(\varepsilon ^{1/2}\).

The drift and diffusion coefficients of the energy process \(\Lambda (t)\) are obtained from (18) and (19) as follows

$$\begin{aligned} m(\Lambda )&= -\gamma \left\langle {\dot{X}^{2}} \right\rangle _t +\int \limits _{-\infty }^0 \left\langle {\frac{X(t)X(t+\tau )\dot{X}(t+\tau )}{\dot{X}(t)}} \right\rangle _t \nonumber \\&\times R_{11} (\tau ) {\text{ d}}\tau +\int \limits _{-\infty }^0 {\left\langle {\frac{\dot{X}(t+\tau )}{\dot{X}(t)}} \right\rangle _t R_{22} (\tau )} {\text{ d}}\tau \end{aligned}$$
(41)
$$\begin{aligned} \sigma ^{2}(\Lambda )&= \int \limits _{-\infty }^\infty {\left\langle {X(t)\dot{X}(t)X(t+\tau )\dot{X}(t+\tau )} \right\rangle _t R_{11} (\tau )} {\text{ d}}\tau \nonumber \\&+\int \limits _{-\infty }^\infty {\left\langle {\dot{X}(t)\dot{X}(t+\tau )} \right\rangle _t R_{22} (\tau )} {\text{ d}}\tau \end{aligned}$$
(42)

In deriving (41), use has been made of Eq. (15) to obtain

$$\begin{aligned} \frac{\partial \dot{X}}{\partial \Lambda }=\frac{1}{\dot{X}} \end{aligned}$$
(43)

4.1 Asymptotic behaviors

Governed by the Itô stochastic differential equation (17) with the drift and diffusion coefficients given by (41) and (42), the two boundaries at \(\Lambda = 0\) and \(\Lambda = \infty \) can be classified based on a theory described by Lin and Cai [8].

As the system approaches the left boundary \(\Lambda = 0, \dot{X}\) approaches zero and \(X\) approaches either \(\sqrt{\alpha /\beta }\) or \(-\sqrt{\alpha /\beta }\). As mentioned previously, the system can be approximated as a linear oscillator around an equilibrium point, with the energy process being

$$\begin{aligned} \Lambda (X,\dot{X})=\frac{1}{2}\dot{X}_e^2 +\alpha X_e^2 \end{aligned}$$
(44)

where \(X_e =X-\sqrt{\alpha /\beta }\), is the random counterpart of \(x_{e}\) given in (10). It can then be shown that

$$\begin{aligned}&m(\Lambda )\rightarrow \pi \frac{\alpha }{\beta }\Phi _{11} (\sqrt{2\alpha })+\pi \Phi _{22} (\sqrt{2\alpha })\quad \text{,} \text{ as} \,\Lambda \rightarrow \text{0}\end{aligned}$$
(45)
$$\begin{aligned}&\sigma ^{2}(\Lambda )\rightarrow 2\pi \Lambda \left[ {\frac{\alpha }{\beta }\Phi _{11} (\sqrt{2\alpha })+\Phi _{22} (\sqrt{2\alpha })} \right] ,\quad \text{ as} \,\Lambda \rightarrow 0 \nonumber \\ \end{aligned}$$
(46)

According to [8], the left boundary \(\Lambda = 0\) is singular of the first kind, and it is an entrance. As the probability flow approaches this boundary, the repulsive force becomes larger, and it forces the system motion back to its defining range.

As \(\Lambda (t)\) approaches the right boundary at infinity, the analytical expressions for \(m (\Lambda )\) and \(\sigma ^{2}(\Lambda )\) are difficult to obtain. But their orders of magnitude can be accessed as follows

$$\begin{aligned} m(\Lambda )\sim \text{ O}(-\Lambda ),\sigma ^{2}(\Lambda )\sim \text{ O}(\Lambda ^{3/2}),\quad \text{ as} \,\Lambda \rightarrow \infty \end{aligned}$$
(47)

where \(\text{ O}(\cdot )\) denotes the order of magnitude. Thus, the right boundary \(\Lambda = \infty \) is singular of the second kind, and is repulsively natural [8], similar to, but weaker than an entrance.

The behaviors of sample functions of process \(\Lambda (t)\) near the two boundaries are represented schematically in Fig. 4. It is concluded that the stationary probability density of \(\Lambda (t)\) exists.

Fig. 4
figure 4

Boundary behaviors of sample functions of process \(\Lambda (t)\)

Full size image

4.2 Stationary probability density

Consider the case of low-pass random processes for the random excitations \(\xi _{1 }(t)\) and \(\xi _{2 }(t)\). The correlation functions are

$$\begin{aligned} R_{ii} (\tau )=D_i e^{-\alpha _i \left| \tau \right| }, \quad i=1,2 \end{aligned}$$
(48)

and the power spectral densities are

$$\begin{aligned} \Phi _{ii} (\omega )=\frac{D_i \alpha _i }{\pi (\omega ^{2}+\alpha _i^2 )} \end{aligned}$$
(49)

where \(\alpha _{i}\) and \(D_{i}\) are the band width and intensity parameters, respectively. A higher \(D_{i}\) corresponds to a stronger excitation, while a larger \(\alpha _{i}\) indicates a broader band, or equivalently, a shorter correlation time. The process is called the low-pass noise since the spectrum peak is at zero frequency (\(\omega = 0\)). Figure 5 depicts the power spectral densities of the low-pass process with \(D_{1} = 0.01\) and three different \(\alpha _{1}\) values. The case of \(\alpha _{1} = 1\) corresponds to a narrow band width, while the process is of broad band if \(\alpha _{1} = 3\).

Fig. 5
figure 5

Power spectral densities of the low-pass process with different band-width parameter \(\alpha _{i}\)

Full size image

Following the procedure proposed in the previous sections, we calculate \(m (\lambda )\) and \(\sigma ^{2 }(\lambda )\) from Eqs. (41) and (42), \(p (\lambda )\) from (23), \(p(x,\dot{x})\) from (27), and finally \(p(x)\) and \(p(\dot{x})\) from (28). The numerical results of the stationary probability density \(p(x)\) are depicted in Fig. 6 for system parameters \(\alpha = 2, \beta = 1, \gamma = 0.015\) and excitation intensities \(D_{1}=D_{2} = 0.01\). Three different values of the band-width parameter \(\alpha _{1}=\alpha _{2}\) are adopted.

Fig. 6
figure 6

Stationary probability densities of system response subjected to low-pass excitations with different band-width parameter \(\alpha _{i}\) values

Full size image

Monte Carlo simulations are performed to assess the accuracy of the proposed method. For computational convenience, the excitations \(\xi _{i }(t)\) are generated from the first-order differential equations

$$\begin{aligned} \dot{\xi }_i +\alpha _i \xi _i =W_i (t), \quad i=1,2 \end{aligned}$$
(50)

where each \(W_{i }(t)\) is a white noise with a spectral density \(K_i =\frac{D_i \alpha _i }{\pi }\). Results from the Monte Carlo simulation are also depicted in Fig. 6 to substantiate the accuracy of the analytical results.

4.3 Mean transition time

Assume that, before exposed to the random excitations, the system energy is \(\lambda _{0}\), which is less than the critical value \(\lambda _c =\alpha ^{2}/(4\beta )\). Upon imposing the excitations, jump to the other well is a random event. The mean transition time of the jump can be calculated from Eqs. (38) and (39). Figure 7 depicts the calculated results, as well as the simulation ones, with the same system parameters as in Fig. 6.

Fig. 7
figure 7

Mean transition time of system subjected to low-pass excitations with different band-width parameter \(\alpha _{i}\) values

Full size image

Figures 6 and 7 show that the band widths of the excitations have significant effects on the system response. It is noticed that, in Fig. 6, the curve for the case \(\alpha _{1}=\alpha _{2} = 3\) is between the curses for \(\alpha _{1}=\alpha _{2} = 1\) and \(\alpha _{1}=\alpha _{2} = 2\), indicating the effect of the band width does not follow a one-way trend. Similar phenomenon is also observed in Fig. 7. Therefore, the effect of the band width also depends on the system properties, more specifically, the range of the system natural frequency.

5 Concluding remarks

A procedure is proposed to apply the stochastic averaging method to systems with double-well potentials or even with potentials of more complicated shapes. The key of the procedure is to use the correlation functions instead of the power spectral densities, as being done in the previous developed versions of the stochastic averaging. Such a way, the drift and diffusion coefficients of the energy process can be calculated separately for different types of motions appearing in the double-well system. Upon extension of the stochastic averaging, dynamical behaviors of a system with a double-well potential, such as the asymptotic behaviors at boundaries, the stationary probability density function, and the transition between two potential wells, can be investigated.