Skip to main content
SpringerLink
Log in

Modeling, analysis and experimental evaluation of boundary threshold limits for Maglev system

  • Published:
International Journal of Dynamics and Control Aims and scope Submit manuscript

Abstract

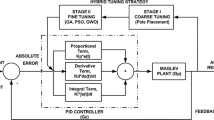
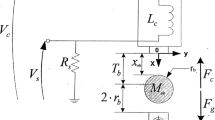
Magnetic Levitation system is an unstable and sensitive system. High precision force balance condition is required to levitate an object in the air. Accurate mathematical modeling, transfer function derivation, linearization and appropriate choice of the controller parameters play an instrumental role in the successful levitation of the object. Selection of the boundary limits for parameter variation of a controller is difficult as linearization conditions impose limitations on the upper and lower bounds. Pole Placement technique has been found to be effective in calculating the parameters of the controller as it takes the closed loop system dynamics into account. In this paper, the poles have been placed at a number of different locations to experimentally analyze the responses to find the threshold limits for successful levitation of the ball in the real time environment.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Jones W (1980) Earnshaw’s theorem and the stability of matter. Eur J Phys 1:85–88 (printed in Northern Ireland)

    Article  Google Scholar 

  2. Yaghoubi H (2013) The most important Maglev applications. J Eng, Article ID 537986

  3. Wong TH (1986) Design of a magnetic levitation control system—an undergraduate project. IEEE Trans Educ 29(4):196–200

    Article  MathSciNet  Google Scholar 

  4. Li Y, Ang KH, Chong GCY (2006) PID control system analysis and design. IEEE Control Syst Mag 26(1):32–41

    Article  Google Scholar 

  5. Astrom KJ, Hagglund T (1995) PID controllers: theory, design and tuning. Instrument Society of America, Pittsburgh

    Google Scholar 

  6. Gopal M (2011) Digital control and state variable method. Tata McGraw Hill, NJ

    Google Scholar 

  7. Ogata K (1997) Modern control engineering. PHI Learning Private Ltd, Englewood Cliffs

    MATH  Google Scholar 

  8. Valasek M, Olgac N (1995) Efficient pole placement technique for linear time-variant SlSO systems. IEEE Proc Control Theory Appl 142(5):451–458

    Article  Google Scholar 

  9. Sujitjorn S, Wiboonjaroen W (2011) State-PID feedback for pole placement of LTI systems. Math Probl Eng 2011:929430

    Article  MathSciNet  Google Scholar 

  10. Dukaa A-V, Dulau M et al (2016) IMC based PID control of a magnetic levitation system. Proc Technol 22:592–599

    Article  Google Scholar 

  11. Levitation Magnetic (2011) Control experiments. Feedback Instruments Limited, London

    Google Scholar 

  12. Hajjaji AE, Ouladsine M (2001) Modeling and nonlinear control of magnetic levitation systems. IEEE Trans Industr Electron 48(4):831–838

    Article  Google Scholar 

  13. Chowdhury A, Golob M et al (2003) Robust controller design for position control of the metal ball in magnetic field. In: IEEE international conference on industrial technology

  14. Nayak A, Subudhi B (2016). Discrete back stepping control of magnetic levitation system with a nonlinear state estimator. In: IEEE annual india conference (INDICON)

  15. Wang L, Freeman C, Rogers E (2017) Experimental evaluation of automatic tuning of PID controllers for an electro-mechanical system. IFAC Pap Line 50(1):3063–3068

    Article  Google Scholar 

  16. Ghosh A, Krishnan TR et al (2014) Design and implementation of a 2-DOF PID compensation for magnetic levitation systems. ISA Trans 53(4):1216–1222

    Article  Google Scholar 

  17. Hamed A, Shaban EM et al (2017) Design and implementation of discrete PID control applied to Bitumen tank based on new approach of pole placement technique. Int J Dyn Control 5:604–613

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors are thankful to the management of BIT Mesra for providing a research friendly atmosphere.

Funding

The authors have not received any financial grants.

Author information

Authors and Affiliations

  1. Department of EEE, Birla Institute of Technology, Mesra, Patna Campus, Bihar Veterinary College Campus, Patna, Bihar, 800014, India

    Shradha Kishore

  2. Department of EEE, Birla Institute of Technology, Mesra, Ranchi, Jharkhand, 835215, India

    Vijaya Laxmi

Authors
  1. Shradha Kishore
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Vijaya Laxmi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shradha Kishore.

Ethics declarations

Conflict of interest

The author declares that they have no conflict of interest.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kishore, S., Laxmi, V. Modeling, analysis and experimental evaluation of boundary threshold limits for Maglev system. Int. J. Dynam. Control 8, 707–716 (2020). https://doi.org/10.1007/s40435-020-00619-w

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40435-020-00619-w

Keywords

Search

Navigation