1 Introduction

Coal and gas outburst (hereafter referred to as outburst) is a destructive disaster that occurs during underground mining, involving violent and spontaneous ejections of gas and coal-rock materials from the mining space (Ma et al. 2020a, b; Guan et al. 2009; Zou et al. 2020; Wu et al. 2020). Since the first recorded outburst occurred in the Isaac Coal Mine in France in 1834, more than 40,000 outbursts have been reported around the world in more than 20 countries, including the US, China, and Germany (Fan et al. 2017; Ma et al. 2020a, b), with China most affected (Zou et al. 2020). Outburst and its resultant secondary disasters can result in serious casualties and property loss (An et al. 2019; Zhai et al. 2016; Zhou et al. 2020). On April 25, 2019, an outburst occurred in Sanjin coal mine in Yunnan Province, killing four miners and leading to a direct economic loss of up to 39.35 million CNY.

Outburst risk is closely related to mining depth. There is a critical buried depth (initial outburst depth) at which an outburst begins to occur in a given coal seam. When the buried depth of a coal seam exceeds the initial outburst depth, the risk and intensity of an outburst generally increase with increasing mining depth (Zhai et al. 2016). In recent years, a phenomenon of low-index outburst with increased mining depth has been observed; this refers to cases where an outburst occurs although the seam had been identified as non-outburst prone based on current indices. This phenomenon is difficult to prevent and can lead to serious loss. Therefore, elucidating the mechanism of outburst, especially low-index outburst, will be conducive to the prediction and prevention of such disasters (An et al. 2019; Yang et al. 2021).

The mechanism of outburst has been studied since 1852, and many hypotheses have been proposed to explain it (Ma et al. 2020a, b; Rudakov and Sobolev 2019; Sobczyk 2011, 2014; Zhi and Elsworth 2016). Most of the models or hypotheses can be classified as pocket models, dynamic models, or multi-factor model (Guan et al. 2009). According to pocket models, there exists a gas-rich and loose zone in front of the working face, and outburst occurs once the gas-rich pocket is uncovered. However, such models can only explain certain special cases encountered in mining practice. A dynamic model assumes that mining disturbance weakens the coal ahead of the working face, which makes it prone to outburst. However, this hypothesis overemphasizes the effects of stress while ignoring the key factor of gas. The multi-factor model proposes that outburst is co-initiated by multiple factors, including geostress, gas pressure, coal strength, and mining disturbance (Ma et al. 2020a, b; An et al. 2019).

In recent decades, progress has been made regarding the mechanism of outburst. Guan et al. (2009) drew an analogy between outburst and magma fragmentation during volcanic eruption. This model considered outburst as an eruption driven by a gas pressure difference, but it ignored other factors such as stress and coal strength. Chen (2011) suggested a domino effect that led to instantaneous outburst, based on the assumption that choked flow in the fracture zone resulted in a large gas pressure gradient, which initiated an outburst. The author claimed that this model could successfully predict all the observed phenomena preceding outbursts. Cao et al. (2020) investigated the initiation and evolution of outburst with micro-fracture mechanics. In this study, pre-set fractures parallel to the working face were assumed to undergo opening, expansion, and propagation driven by gas pressure. This process was modeled by setting a criterion assuming that outburst occurred once the fracture length exceeded the host element dimension. Based on analyses of the external environment of outbursts, Shu et al. (2017) proposed a key structural body model of outbursts. Based on this model, a mechanical criterion and an energy criterion for outburst initiation were developed. Fan et al. (2017) suggested that outburst was caused by interactions among coal–gas media, the geology dynamic environment, and mining disturbance, and developed a stress-seepage-damage coupling model to simulate the evolution of the outburst dynamic system. Based on this system, they also proposed a formation criterion for the geological dynamic system, an instability criterion, and an energy criterion (Luo et al. 2018). Lu et al. (2019) proposed an energy criterion for outbursts under deformed and normal coal combinations. Combining this with a coupled fluid–solid model, they simulated the distribution and components of energy ahead of the working face. An et al. (2019) found that coal damage had an effect on gas expansion energy during outburst initiation. Based on fractal theory, they modified the existing models of gas desorption and gas expansion energy.

Although previous research has clearly shown that stress, gas pressure, and coal strength are the main factors controlling outbursts, there have been few reports on how these factors interact with each other to induce outburst. In addition, most of the previously proposed hypotheses only give qualitative descriptions of the initiation mechanism; few quantitative studies have been reported.

In this work, we attempt to clarify the mechanism of outburst from a multiphysics coupling perspective. First, based on the equivalent fractured coal model, a multiphysics coupling model is developed and verified. Next, a risk identification index and critical criterion are proposed to determine the risk and initiation of outburst. Using the coupled model, factors influencing the risk identification index are systematically studied. Finally, a mechanism of multiphysics-coupling-induced outburst is described and a classified control method is proposed.

2 Modeling

2.1 Constitutive stress–strain equation

The deformation of coal containing methane can generally be expressed by Eq. (1), considering pore pressure and sorption-induced swelling (Liu et al. 2020a):

$$Gu_{{i,kk}} + \frac{G}{{1 - 2\nu }}u_{{k,ki}} - \alpha p_{{fi}} - \beta p_{{mi}} - K\Delta \varepsilon _{{mi}}^{s} + F_{i} = 0$$
(1)

where, G is the shear modulus of coal, \(G = E/2\left( {1 + \nu } \right)\); E is the elastic modulus of coal; \(\nu\) is the Poisson’s ratio of coal; \(F_{i}\) is the body force in the ith direction; \(\alpha\) and \(\beta\) are Boit’s coefficients of the fracture and the pore, respectively, \(\alpha {\text{ = }}1 - {K \mathord{\left/ {\vphantom {K {K_{\rm f} }}} \right. \kern-\nulldelimiterspace} {K_{\rm f} }}\), \(\beta {\text{ = }}1 - {K \mathord{\left/ {\vphantom {K {K_{\rm s} }}} \right. \kern-\nulldelimiterspace} {K_{\rm s} }}\); \(p_{\rm f}\) and \(p_{\rm m}\) are the gas pressures in the fracture and the matrix, respectively; K is the bulk modulus of coal, \(K = E/3\left( {1 - 2\nu } \right)\); and \(\varepsilon _{\rm m}^{\rm s}\) is the matrix strain induced by gas sorption, \(\varepsilon _{\rm m}^{\rm s} {\text{ = }}{{\varepsilon _{\rm L} p_{\rm m} } \mathord{\left/ {\vphantom {{\varepsilon _{\rm L} p_{\rm m} } {\left( {p_{\varepsilon } + p_{\rm m} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {p_{\varepsilon } + p_{\rm m} } \right)}}\), with \(\varepsilon _{\rm L}\) the Langmuir-type strain constant and \(p_{\varepsilon }\) the Langmuir-type pressure constant.

Owing to disturbance by mining, failure often occurs in coal ahead of the working face. In this work, the Drucker–Prager matching Mohr–Coulomb criterion was adopted to describe coal failure ahead of the working face:

$$F - \left( {\sqrt {J_{2} } - \alpha _{{{\rm D} - {\rm P}}} I_{1} - k_{{{\rm D} - {\rm P}}} } \right) = 0$$
(2)

where, J2 is the second deviatoric stress invariant and I1 is the first stress invariant. Here, \(\alpha _{{{\rm D} - {\rm P}}}\) and \(k_{{{\rm D} - {\rm P}}}\) are material constants given by Eq. (3):

$$\left\{ \begin{gathered} \alpha _{{{\rm D} - {\rm P}}} = \frac{{2\sin \phi }}{{\sqrt 3 \left( {3 - \sin \phi } \right)}} \hfill \\ k_{{{\rm D} - {\rm P}}} = \frac{{2\sqrt 3 C\cos \phi }}{{\left( {3 - \sin \phi } \right)}} \hfill \\ \end{gathered} \right.$$
(3)

where C and \(\phi\) are the cohesion and the internal friction angle, respectively.

In addition to shear failure, tensile failure can occur in a coal seam during the mining process. The failure criterion for tensile failure of coal can be expressed by Eq. (4):

$$f_{\rm t} = - \sigma _{1}^{\rm {eff}} - \sigma _{\rm t}$$
(4)

where, \(\sigma _{\rm t}\) is the tensile strength of coal, and the minus sign indicates the tensile stress; when ft ≥ 0, coal failure occurs.

2.2 Changes in coal strength during mining

2.2.1 Cohesion and internal friction angle

Given a set of stress–strain curves obtained under different confining stresses, the strength parameters of coal at and after the peak can be calculated. The detailed process can be found in reference (Jing et al. 2018).

Figure 1 shows the cohesion and the internal friction angle corresponding to peak and residual points calculated using 15 groups of stress–strain curves collected from the literature. As shown in Fig. 1a, all the cohesion values corresponding to the residual points are lower than those of the peak points, indicating that the decrease in cohesion after the peak represents a universal law. Relative changes in cohesion ranged between 30% and 90%, with an average of 59.8%, demonstrating that cohesion decreases greatly after failure. As shown in Fig. 1b, most of the increments in internal friction angle were in the range of ± 10%, with an average of − 4.3%. This implies that the internal friction angle does not change significantly after coal failure and can thus be considered as a constant.

Fig. 1
figure 1

Statistical results for cohesion and internal friction angle. (Cr-Cp) and (θr-θp) are the differences in cohesion and internal friction angle between residual and peak points, respectively; RC indicates relative change: RC = (Cr-Cp)/Cp or RC = (θr-θp)/θp

Full size image

A series of models have been developed to quantify the relationship between cohesion and plastic strain, including models based on the exponential function, quadratic function, linear function, and some complex composite functions (Li et al. 2016). Jing et al. (2018) theoretically proved that cohesion changed linearly with hoop strain in the plastic softening zone. In this work, a linear relation between cohesion and equivalent plastic strain is adopted (Alonso et al. 2003):

$$C = \left\{ {\begin{array}{*{20}c} {C_{0} - \left( {C_{0} - C_{\rm r} } \right)\frac{{\gamma ^{\rm p} }}{{\gamma ^{{\rm p * }} }},} & {0 \le \gamma ^{\rm p} \le \gamma ^{{\rm p * }} } \\ {C_{\rm r} ,} & {\gamma ^{\rm p} > \gamma ^{{\rm p * }} } \\ \end{array} } \right.$$
(5)

where C is the cohesion of coal, C0 is the initial cohesion of coal, Cr is the residual cohesion, \(\gamma ^{\rm p}\) is the equivalent plastic strain, and \(\gamma ^{\rm {p * }}\) is the equivalent plastic strain at the start of the residual stage.

2.2.2 Tensile strength

Assuming that coal follows the Mohr–Coulomb criterion and is in the uniaxial tensile state, we have

$$\sigma _{1} = \sigma _{2} = 0,\quad \sigma _{3} = \sigma _{t}$$
(6)

When the coal is in the triaxial tension state, the shear stress imposed is 0. Assuming that the Mohr circle is tangent to the yield surface, where coal is in the ultimate tensile state, we can obtain its tensile strength (Chen and Jin 2012) as follows:

$$\sigma _{t} = \frac{{2C}}{{\tan \phi + \sqrt {1 + \tan ^{2} \phi } }}$$
(7)

2.3 Quantitative characterization of mining-disturbed coal

Quantitative characterization of the coal structure is among the most important problems that arises in the study of gas flow in a mining-disturbed coal seam. To solve this problem, an equivalent fractured coal model was proposed in our previous work (Liu et al. 2020b). In this model, the generation of new fractures is viewed as a segmentation of the matrix, and the mining-disturbed coal can be viewed as an elastomer containing a smaller matrix and more fractures. Figure 2 shows a diagram of the equivalent fractured coal model and its application in describing the coal structure ahead of the working face.

Fig. 2
figure 2

Equivalent fractured coal model and its application in fracture characterization ahead of the working face. a primary coal; b coal disturbed by mining; c equivalent fractured coal; d fracture distribution ahead of the working face

Full size image

Based on the equivalent fractured model, the matrix size in mining-disturbed coal seam can be quantified by Eq. (8) (Liu et al. 2021):

$$L_{m} = \frac{1}{{n_{\rm {matrix}} + 1}}L_{{\rm m}0} = \frac{{\phi _{{\rm f}0} }}{{\varepsilon _{\rm b}^{\rm p} + \phi _{{\rm f}0} }}L_{{\rm m}0}$$
(8)

where, Lm0 is the initial matrix size, nmatrix is the number of new fractures in the specified direction of the matrix, \(\varepsilon _{\rm b}^{\rm p}\) is the plastic strain of coal, and \(\phi _{{\rm f}0}\) is its initial fracture porosity, with \(\phi _{{\rm f}0} {\text{ = }}{{3L_{{\rm f}0} } \mathord{\left/ {\vphantom {{3L_{{\rm f}0} } {L_{{\rm m}0} }}} \right. \kern-\nulldelimiterspace} {L_{{\rm m}0} }}\) (Liu et al. 2017; Wu et al. 2011).

2.4 Governing equation of gas migration in coal matrix

In virgin coal seams, mass transfer between coal matrices and fractures can be expressed by Fick’s law (Fan et al. 2019):

$$Q_{\rm m} = \frac{1}{\tau }\frac{{M_{\rm C} }}{{RT}}\left( {p_{\rm m} - p_{\rm f} } \right)$$
(9)

where, \(Q_{\rm m}\) is the mass transfer capacity; \(M_{\rm C}\), R, and T are the molar mass of CH4, the gas constant, and the temperature of the coal seam, respectively; τ is the sorption time, \(\tau = {{L_{\rm m} ^{2} } \mathord{\left/ {\vphantom {{L_{\rm m} ^{2} } {\left( {3\pi ^{2} D} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {3\pi ^{2} D} \right)}}\); and D is the gas diffusivity of coal.

Mining disturbance changes the structure of the coal ahead of the working face, which in turn alters the diffusion path of gas in the matrix. The sorption time of mining-disturbed coal can be expressed by Eq. (10):

$$\tau = \left( {\frac{{\phi _{{\rm f}0} }}{{\varepsilon _{\rm b}^{\rm p} + \phi _{{\rm f}0} }}} \right)^{2} \cdot \frac{{L_{{\rm m}0} ^{2} }}{{3\pi ^{2} D}} = \left( {\frac{{\phi _{{\rm f}0} }}{{\varepsilon _{\rm b}^{\rm p} + \phi _{{\rm f}0} }}} \right)^{2} \cdot \tau _{0}$$
(10)

where, τ0 is the sorption time of a virgin coal seam.

Based on mass conservation, a governing equation for gas diffusion in virgin coal seams was developed (Lu et al. 2019). Combining this with Eq. (10), we can further obtain the governing equation of gas diffusion in mining-disturbed coal seams:

$$\frac{\partial }{{\partial t}}\left\{ {\frac{{M_{\rm C} \rho _{\rm c} }}{{V_{\rm m} }} \cdot \frac{{V_{\rm L} p_{\rm m} }}{{p_{\rm L} + p_{\rm m} }} + \phi _{\rm m} \frac{{M_{\rm C} p_{\rm m} }}{{RT}}} \right\} = - \left( {\frac{{\phi _{{\rm f}0} + \varepsilon _{\rm b}^{\rm p} }}{{\phi _{{\rm f}0} }}} \right)^{2} \cdot \frac{1}{{\tau _{0} }} \cdot \frac{{M_{\rm C} }}{{RT}}\left( {p_{\rm m} - p_{\rm f} } \right)$$
(11)

where ρc is the coal density, Vm is the molar volume of gas, VL and pL are Langmuir constants, and \(\phi _{\text{m}}\) is the matrix porosity.

2.5 Governing equation of gas flow in fracture

The change in gas content in a fracture is the difference between the gas inflow and outflow (Danesh et al. 2016). Combining Darcy’s law and Eq. (10), we can obtain the following controlling equation for gas flow in fractures in mining-disturbed coal seams:

$$\phi _{\rm f} \frac{{\partial p_{\rm f} }}{{\partial t}} + p_{\rm f} \frac{{\partial \phi _{\rm f} }}{{\partial t}} - \nabla \left( {\frac{k}{\mu }p_{\rm f} \nabla p_{\rm f} } \right) = \left( {\frac{{\phi _{{\rm f}0} + \varepsilon _{\rm b}^{\rm p} }}{{\phi _{{\rm f}0} }}} \right)^{2} \cdot \frac{1}{{\tau _{0} }} \cdot \left( {p_{\rm m} - p_{\rm f} } \right)$$
(12)

where, \(\mu\) is the dynamic viscosity of CH4 and k is the coal permeability.

2.6 Coupling term

We have developed a porosity model of a mining-disturbed coal seam that considers the effects of stress change, matrix shrinkage, and coal failure, which has been shown in Eq. (13). In this model, when the coal is in the elastic stage, the porosity is dominated by the stress change and matrix shrinkage. At the strain-softening stage, porosity increases sharply because of the coal failure, whereas no obvious change occurs in the residual stage (Liu et al. 2021):

$$\frac{{\phi _{\rm f} }}{{\phi _{{\rm f}0} }} = \left\{ {\begin{array}{*{20}c} {\frac{{\phi _{{\rm f}0} + \varepsilon _{\rm b}^{\rm p} }}{{\phi _{{\rm {fi}}0} }}\left( {1 - \frac{3}{{\phi _{{\rm f}0} }}\left( {\varepsilon _{\rm m}^{\rm s} - \varepsilon _{{\rm m}0}^{s} } \right) - \frac{{\Delta \sigma ^{\rm{eff}} }}{{K_{\rm f} }}} \right)} & {\left( {\varepsilon _{\rm b}^{\rm p} \le \varepsilon _{\rm {bc}}^{\rm p} } \right)} \\ {\frac{{\phi _{{\rm f}0} + \varepsilon _{\rm {bc}}^{\rm p} }}{{\phi _{{\rm f}0} }}\left( {1 - \frac{3}{{\phi _{{\rm f}0} }}\left( {\varepsilon _{\rm m}^{\rm s} - \varepsilon _{{\rm m}0}^{\rm s} } \right) - \frac{{\Delta \sigma ^{\rm {eff}} }}{{K_{\rm f} }}} \right)} & {\left( {\varepsilon _{\rm b}^{\rm p} > \varepsilon _{\rm {bc}}^{\rm p} } \right)} \\ \end{array} } \right.$$
(13)

where, \(\phi _{\rm f}\) is the fracture porosity, \(\varepsilon _{\rm {bc}}^{\rm p}\) is the plastic volumetric strain corresponding to the starting point of the residual stage, \(\Delta \sigma ^{\rm {eff}}\) is the increment of effective stress, and \(K_{\rm f}\) is the bulk modulus of fractures (the subscript ‘0’ indicates the initial value).

According to the cubic law, the permeability of the coal seam can be described by Eq. (14) (Liu et al. 2021):

$$\frac{k}{{k_{0} }} = \left( {\frac{{\phi _{\rm f} }}{{\phi _{{\rm f}0} }}} \right)^{3} = \left\{ {\begin{array}{*{20}c} {\left[ {\frac{{\phi _{{\rm f}0} + \varepsilon _{\rm b}^{\rm p} }}{{\phi _{{\rm f}0} }}\left( {1 - \frac{3}{{\phi _{{\rm f}0} }}\left( {\varepsilon _{\rm m}^{\rm s} - \varepsilon _{{\rm m}0}^{\rm s} } \right) - \frac{{\Delta \sigma ^{\rm {eff}} }}{{K_{\rm f} }}} \right)} \right]^{3} } & {\left( {\varepsilon _{\rm b}^{\rm p} \le \varepsilon _{\rm {bc}}^{\rm p} } \right)} \\ {\left[ {\frac{{\phi _{{\rm f}0} + \varepsilon _{\rm{bc}}^{\rm p} }}{{\phi _{{\rm f}0} }}\left( {1 - \frac{3}{{\phi _{{\rm f}0} }}\left( {\varepsilon _{\rm m}^{\rm s} - \varepsilon _{{\rm m}0}^{\rm s} } \right) - \frac{{\Delta \sigma ^{\rm {eff}} }}{{K_{\rm f} }}} \right)} \right]^{3} } & {\left( {\varepsilon _{\rm b}^{\rm p} > \varepsilon _{\rm {bc}}^{\rm p} } \right)} \\ \end{array} } \right.$$
(14)

To solve the gas diffusion equation in a matrix, it is necessary to consider matrix porosity. In this work, the matrix porosity model developed in Liu et al. (2020a) is adopted:

$$\phi _{\rm m} = \phi _{{\rm m}0} \exp \left\{ {\frac{{1 - \phi _{{\rm m}0} }}{{\phi _{{\rm m}0} }}\left[ {\varepsilon _{\rm m}^{\rm s} - \varepsilon _{{\rm m}0}^{\rm s} - \frac{{\Delta \sigma _{\rm e} }}{{K_{\rm m} }}} \right]} \right\}$$
(15)

where, \(\phi _{{\rm m}0}\) is the initial porosity of the matrix and Km is the bulk modulus of the matrix.

2.7 Mechanical criterion for outburst

Outburst is a result of mechanical instability of coal ahead of the working face, arising under the combined action of crustal stress and gas pressure. In this section, a critical criterion for outburst during roadway excavation is developed by analyzing the stress imposed on a representative element volume (REV) of coal ahead of the working face.

During roadway excavation, the redistribution of stress and gas pressure leads to instability of coal near the working face (Fig. 3a). To explore the critical conditions for coal instability, we analyzed the stress distributions along the heading direction of the working face using a REV of coal of unit size (Fig. 3a). This analysis shows that stress and gas pressure increments constitute the driving force behind an outburst (Fig. 3b), while the resistance depends on the shear and tensile strengths of coal (Fig. 3c). The critical condition for instability of a REV can be written as

$$\left( {\sigma _{x} + \frac{{\text{d}\sigma _{x} }}{{\text{d}x}}} \right) - \sigma _{x} + \left( {p_{x} + \frac{{\text{d}p_{x} }}{{\text{d}x}}} \right) - p_{x} \ge 2\left( {\sigma _{y} \tan \phi + C} \right) + 2\left( {\sigma _{z} \tan \phi + C} \right) + \sigma _{t}$$
(16)

where \(\sigma _{x}\), \(\sigma _{y}\), and \(\sigma _{z}\) are stresses along the x-, y-, and z-directions, respectively; x is the distance from the coal wall; and px is the gas pressure at the point with coordinate x.

Fig. 3
figure 3

Stress analysis of REV ahead of the working face

Full size image

Rewriting Eq. (16), we obtain the critical criterion for coal instability ahead of the working face:

$$C_{\rm m} = \frac{{\frac{{\text{d}\sigma _{x} }}{{\text{d}x}} + \frac{{\text{d}p_{x} }}{{\text{d}x}}}}{{2\tan \phi \left( {\sigma _{y} + \sigma _{z} } \right) + 4C + \sigma _{\rm t} }} \ge 1$$
(17)

where, Cm is the risk identification index of the outburst (if Cm < 1, the system remains stable; if Cm = 1, the system is in a state of critical instability; and if Cm > 1, the system is not stable).

Equation (17) shows that driving force behind an outburst consists of gradients of horizontal stress and gas pressure along the heading direction of the roadway, rather than the horizontal stress and gas pressure themselves. The risk of outburst rises as the gradients of horizontal stress and gas pressure increase. The resistance is mainly derived from the stresses perpendicular to the heading direction, the shear strength of the coal or the coal-rock interface, and the tensile strength of the coal. It is clear from Eq. (17) that the greater the stresses perpendicular to the heading direction, the more stable the coal. However, increases in \(\sigma _{y}\) and \(\sigma _{z}\) cause changes in \(\sigma _{x}\), resulting in failure of the coal seam, which in turn increases the outburst risk. Therefore, the effects of stress on outburst risk are complex and should be analyzed based on the specific situation. Moreover, as the shear and tensile strengths of coal increase, the risk of outburst decreases; in previous research, the effect of tensile strength was often ignored, which may overestimate the outburst risk.

3 Case study of outburst and model verification

3.1 Introduction of outburst case study

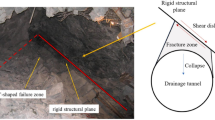
From April 1991 to January 1992, 286 m of roadway (J15-13,170 machine and equipment roadways) was excavated in No. 8 coal mine of Pingdingshan Coal Co., Ltd, in Henan Province, China. During this period, eight outbursts occurred, with an average frequency of 2.8 per 100 m of roadway. The intensity of coal outburst and volume of gas were 781 t and 41,900 m3, respectively, with mean outburst intensity and gas volume of 97.6 t and 5237.5 m3, respectively. The dynamic effects of these outbursts are obvious. Support deformation and downward movement were observed several times; the most prominent type of outburst was extrusion, which accounted for 87.5% of the total. Before the outbursts, a series of precursors were observed, including coal and gas blowout from boreholes, increases in gas emission, and coal bedding disorder.

Figure 4 shows the locations of the eight outbursts. The J15-13,170 machine and equipment roadways were located in the lower section of the J15-13,170 working face, with an opening elevation of − 490.29 m and buried depth of 566.0 m. The thickness and dip angle of the coal seam in this area were 3.5–4.0 m and 16°, respectively, and the roof and floor were sandy mudstone with poor permeability. The gas pressure and gas content were 1.47 MPa and 10.08 m3/t, respectively.

Fig. 4
figure 4

Locations of the eight outbursts in J15-13,170 machine equipment lanes in No. 8 coal mine

Full size image

3.2 Case analysis and model verification

Based on the eight outbursts that occurred in the J15-13,170 machine and equipment lanes in No. 8 coal mine, we explored the cause of the frequent outbursts in this location from the perspective of multiphysics coupling. We also compared the results calculated with the new model and those obtained with the model ignoring the effect of coal failure.

Figure 5 shows the physical model used to simulate outbursts. The model was 30 m in both length and width, and 14 m in height. The thickness of the coal seam, roof, and floor were 4, 5, and 5 m, respectively. The size of the excavated zone was 4 m × 3.2 m × 2 m. The top of the model was set as the stress boundary with a constant stress of 15 MPa to simulate a buried depth of approx. 550 m. The four sides were set as the roller boundary, and the bottom was fixed. The initial gas pressure of the coal seam was specified as 1.5 MPa. The roadway wall was set as a Dirichlet boundary with a given pressure of 0.1 MPa to simulate atmospheric pressure, and the four sides of the coal seam and the coal–rock interface were set as a non-flow boundary.

Fig. 5
figure 5

Physical model for simulating outburst

Full size image

The other parameters used as inputs to the model are listed in Table 1.

Table 1 Input parameters for the model
Full size table

The results of field tests in Zhongliangshan coal mine showed that three occurrences of impact sound caused by outburst were detected, at 2.5 s, 3.5 s, and 4 s after blasting (Lu et al. 2019). In this work, the distribution of the risk identification index Cm of outburst in the coal ahead of the working face was analyzed using the time point 2 s after excavation as an example; the results are shown in Fig. 6. According to calculations with the new model, Cm was greater than 60 (Cm ≫ 1) on the coal wall, indicating a high outburst risk. With increasing distance from the coal wall, Cm decreased sharply to 1 at a point 1.17 m from the coal wall (x = 3.17 m). The above analyses demonstrate that in this case, extrusion or outburst occurred in coal within approx. 1.2 m of the working face, consistent with the fact that eight outbursts occurred in practice. However, when the effects of coal failure were ignored, Cm at any position ahead of the working face was lower than 1 (red dotted line in Fig. 6), indicating that instability would not occur in this case; this result was contrary to the actual observations. This comparison demonstrates the superiority of the new model and the critical outburst criterion.

Fig. 6
figure 6

Distribution of Cm in coal ahead of the working face

Full size image

4 Mechanism of multiphysics-coupling-induced outburst

4.1 Main factors controlling C m

The critical criterion in Eq. (17) shows that outburst is mainly controlled by stress and its gradient, the coal strength, and the gas pressure gradient. Coal permeability also has an important effect on the distribution of gas pressure. Therefore, in this section, we analyze the influence of stress, coal strength, gas pressure, and permeability on Cm. The results are shown in Fig. 7.

Fig. 7
figure 7

Effects of various factors on Cm. a \(\sigma _{{\text{v}}}\); b C0; c \(\phi\); d pf0; e k0

Full size image

As shown in Fig. 7a, Cm initially decreased slightly, followed by a sharp increase with increasing σv. When σv increased from 4 to 6 MPa, Cm decreased from 0.93 to 0.74. Thereafter, when σv rose to 13 MPa, Cm increased sharply to 16.72. This was because when σv is relatively low (corresponding to a small buried depth), coal failure will not occur. In this case, the shear strength of the coal seam increases with an increase in stress, resulting in a low risk of outburst. When σv is relatively high (corresponding to a large buried depth), the coal seam is easily damaged as the stress increases, and outburst is more likely to occur in this case.

Figure 7b and c show the changes in Cm with cohesion C0 and internal friction angle \(\phi\). Overall, Cm showed an initial rapid decrease, followed by a gentle reduction as C0 and \(\phi\) increased. When C0 increased from 0.5 MPa to 1 MPa, Cm decreased from 9.08 to 1.15, but when C0 increased from 1 to 2 MPa, Cm was only reduced by 0.69. When \(\phi\) increased from 23° to 30°, Cm decreased from 3.51 to 0.56, whereas when \(\phi\) increased from 30° to 40°, Cm was only reduced by 0.1. This was because increases in C0 and \(\phi\) enhance the ability of coal to resist instability, thereby reducing the risk of outburst. When C0 and \(\phi\) are small, coal is prone to failure. With increasing C0 and \(\phi\), the ability of coal to resist failure increases rapidly, and the risk of outburst decreases significantly. When C0 and \(\phi\) are large, coal is unlikely to fail; in this case, increases in C0 and \(\phi\) have little effect on the outburst risk.

As shown in Fig. 7d, Cm increased with as the gas pressure pf0 increased. When pf0 increased from 0.2 MPa to 3 MPa, Cm rose from 0.29 to 2.34. In this case, when the gas pressure is lower than 1.4 MPa, outburst will not occur.

Figure 7e shows the change in Cm with the initial permeability of the coal seam, k0. In general, the lower the permeability of the coal, the higher the risk of coal instability. That is, a coal seam with low permeability is more prone to outburst. When k0 increased from 10–5 mD to 10 mD, Cm decreased from 2.7 to 2.42, with a reduction of less than 10%. This implies that the effect of permeability on Cm is not significant compared with those of the vertical stress, cohesion, internal friction angle and gas pressure.

4.2 Multi-factor coupling model of C m

The above results indicate that stress, coal strength, and gas pressure are the key factors affecting outburst; however, these factors are not independent of each other. In this section, based on the response surface method (RSM), we study the change of Cm under a multi-factor coupling effect and develop a multi-factor coupling model for Cm.

The central composite design module embedded in Design-Expert 12 was used for the design, with four factors and three levels, and a total of 30 sets of parameter combinations were obtained. Through numerical calculations, the values of the risk identification index Cm under the corresponding conditions were obtained. Using RSM, we obtained the following multi-factor coupling model for Cm:

$$\begin{aligned} C_{\rm m} = & 7.84 + 1.66\sigma _{\text{v}} - 15.28C_{0} - 0.24\phi + 1.52p_{{\rm f}0} - 0.55\sigma _{\text{v}} C_{0} - 0.07\sigma _{\text{v}} \phi \\ - 0.12\sigma _{\text{v}} p_{{\rm f}0} + 0.60C_{0} \phi + 0.07\sigma _{\text{v}}^{2} \quad (R^{2} = 0.912) \\ \end{aligned}$$
(18)

The fitting coefficient of this model was R2 = 0.912, indicating that the model matched well with the numerical results. In addition, the corresponding p-values of all items in the model were less than 0.05, indicating that the effects of each item in the model on Cm were significant.

Equation (18) indicates that interactions exist between σv and C0, σv and \(\phi\), σv and pf0, and C0 and \(\phi\), as shown in Fig. 8. The shape of the surface directly reflects the intensity of the interactions between the factors; the larger the curvature of the surface, the stronger the interaction.

Fig. 8
figure 8

Effects of interactions of different factors on Cm. a σv and C0; b σv and \(\phi\); c σv and pf0; d C0 and \(\phi\)

Full size image

As shown in Fig. 8a, as σv increased, Cm initially decreased, followed by an increase; by contrast, it decreased monotonically with increasing C0, consistent with the results shown in Fig. 7a and b. With increasing in-situ stress, the response surface became steeper, indicating that the greater the buried depth of the coal seam, the more significant the influence of C0 on outburst. With decreasing C0, the effect of in-situ stress on Cm became more significant, indicating that the effect of in-situ stress on the outburst risk of soft coal seam was more significant. The contour of Cm = 1 shows that with increasing σv, the critical value of C0 corresponding to coal instability initially decreased and then increased, indicating that the coal strength corresponding to outburst is not a constant but changes with the stress state. Converting the shear strength (C0 and \(\phi\)) into Protodyakonov's coefficient f (\(f = {{C_{0} \cos \phi } \mathord{\left/ {\vphantom {{C_{0} \cos \phi } {5\left( {1 - \sin \phi } \right)}}} \right. \kern-\nulldelimiterspace} {5\left( {1 - \sin \phi } \right)}}\), which can be derived based on the definition of f and the relation between the uniaxial compressive strength and shear strength), it can be seen that when σv increased from 6.5 MPa to 8 MPa, the critical value of f reduced from 0.36 to 0.32. Thereafter, it increased continuously, and when σv = 12 MPa, the critical value of f was greater than 0.4. Figure 8b shows that the effects of σv and \(\phi\) on Cm were similar to those shown in Fig. 8a.

As shown in Fig. 8c, with increasing stress, Cm initially decreased and then increased, whereas with increasing gas pressure, Cm increased monotonically. With decreasing in-situ stress, the effect of gas pressure on Cm became more significant; conversely, with decreasing gas pressure, the effect of in-situ stress on Cm became more significant. As can be seen from the contour of Cm = 1, with increasing σv, the critical gas pressure initially increased, followed by a decrease, indicating that the gas pressure corresponding to an outburst is not a constant but changes with the stress state. For example, when σv = 6 MPa, the critical gas pressure was 1.7 MPa; when it increased to 8 MPa, the critical gas pressure increased to 2.0 MPa; with a further increase of σv to 10.5 MPa, the critical gas pressure reduced to 0.5 MPa and thereafter decreased continuously as σv continued to increase.

As shown in Fig. 8d, with increasing C0 and \(\phi\), Cm decreased monotonically, consistent with the results shown in Fig. 8b and c. The response surface was approximately planar, implying a relatively weak interaction. Moreover, in different coals, the cohesion and internal friction angle usually decrease or increase at the same time. Therefore, the interaction between them is not discussed here.

In summary, the critical value of the parameters corresponding to outburst are not constants but depend on the environment of the coal seam. The main conclusions drawn in this section can be used to reasonably interpret the phenomenon of low-index outburst encountered in mining practice. In March 2014, a major outburst occurred in the 21,010 machine roadway of Yuxi coal mine in Yunnan province, China. This incident involved outburst amounts of coal and gas of 970 t and 31,381 m3, respectively. The buried depth of the outburst site was 498 m, and the vertical stress was ~ 10.6 MPa. The gas content and gas pressure were in the ranges 3.16–5.63 m3/t and 0.06–0.28 MPa, respectively, and the f value was in the range 0.11–0.27 with an average value of 0.19. Importantly, the outburst occurred despite the gas pressure being much lower than the critical value of 0.74 MPa given in the Regulations on Prevention and Control of Coal and Gas Outburst of China. Given the high vertical stress and low f value, we can deduce that the critical gas pressure corresponding to outburst in this case was much lower than 0.74 MPa.

4.3 Mechanism of multiphysics-coupling-induced outburst and method for its control

Previous research has shown that outburst is the result of the co-action of stress, gas pressure, and coal strength. When the driving force is greater than the resistance, coal instability occurs. However, there has been no clear explanation of how an outburst occurs as a direct consequence of the interactions among stress, gas pressure, and coal strength. In this section, we attempt to determine the mechanism of outburst from the perspective of multiphysics coupling, and propose a classified control method.

Figure 9a depicts the initiation process of an outburst. During mining, when a virgin coal seam is exposed, physical parameters including stress and gas pressure, and the mechanical properties of the coal ahead of the working face retain their original values. With increasing exposure time, the physical properties ahead of the working face interact and adjust dynamically. The interactions among stress, gas pressure, and coal strength are presented in Fig. 9b. The change in stress results in coal failure and creates a highly fractured zone ahead of the working face. In this fractured zone, the permeability of the coal increases greatly, and gas is rapidly released from the coal seam, which greatly alters the gas pressure distribution. Furthermore, the stress concentration ahead of the working face leads to an increase in gas pressure in the corresponding zone, which in turn intensifies the driving force of the outburst. In addition, in the damaged zone ahead of the working face, the coal strength is weakened because of plastic deformation, which in turn reduces the resistance against outburst. Changes in gas pressure distribution can also affect the coal deformation that occurs ahead of the working face, which indirectly affects the coal strength. During the adjustment of the physical properties, if the distributions of these properties meet the critical criterion for outburst, coal instability occurs and initiates an outburst. After the first ejection of unstable coal, outburst develops via a domino effect until the critical criterion is no longer satisfied.

Fig. 9
figure 9

Mechanism of multiphysics-coupling-induced outburst and its classified control method

Full size image

Based on the mechanism of multiphysics-coupling-induced outburst, we divide outbursts into the following four types according to their controlling factors and recommend corresponding control methods, as depicted in Fig. 9c.

Type I: stress-dominated outburst. This type of outburst occurs when the buried depth of the corresponding coal seam is large and it is subjected to relatively high stress. The main factor controlling coal instability is the stress gradient. In this type of coal seam, the outburst risk can be significantly reduced by measures such as protective seam mining or borehole stress relief.

Type II: coal-strength-dominated outburst. This type of outburst tends to occur in a coal seam that is located in a tectonic area with low strength (usually called a soft coal seam). In this type of coal seam, reservoir modification measures such as grouting reinforcement can be adopted to enhance the coal strength and thereby reduce the outburst risk.

Type III: gas-pressure-dominated outburst. This type of outburst usually occurs in a coal seam with a small buried depth and a dense roof and floor. Owing to the good storage conditions, the gas pressure is relatively high. In this type of coal seam, artificial measures to enhance gas drainage can significantly reduce the risk of outburst.

Type IV: multi-factor compound outburst. These outbursts usually occur in coal seams that are deeply buried, with a high gas pressure and a low strength, which have a high risk of outburst. It is difficult to achieve an ideal outburst elimination effect using a single measure in this type of coal seam. Therefore, a trinity of comprehensive measures comprising stress relief, gas drainage, and reservoir modification should be adopted to eliminate the risk of outburst.

5 Conclusions

In this work, we developed a multiphysics coupling model and a critical criterion for outburst. The factors controlling the outburst risk identification index in this model were discussed. The main conclusions are as follows.

The multiphysics coupling model was developed based on the equivalent fractured coal model. This model systematically considers coal failure induced by mining, weakening of coal strength in a mining-disturbed zone, and effects of coal failure on mass transfer of gas. The results of the calculations indicate that there is a high risk of outburst in the J15-13,170 machine roadway of the No. 8 coal mine, consistent with the engineering practice.

Based on force analysis of coal ahead of the working face, we propose a risk identification index Cm and a critical criterion for outburst. According to this index, the driving force for an outburst consists of stress gas pressure gradients along the heading direction of the roadway, whereas the outburst resistance depends on the shear and tensile strengths of the coal. The results show that Cm decreases slightly followed by a rapid increase with increasing vertical stress, whereas it increases monotonically with increasing gas pressure and decreases with increasing coal strength.

Multiphysics coupling changes the critical values of parameters corresponding to an outburst. With increasing buried depth, the critical values of gas pressure and coal strength initially decrease slightly, followed by a rapid increase. Therefore, the critical values of parameters corresponding to outburst are not constants but should be determined according to the specific environment of the coal seams.

Based on its controlling factors, outburst can be divided into four types: stress-dominated outburst, coal-strength-dominated outburst, gas-pressure-dominated outburst, and multi-factor compound outburst. Using this classification, a classified control method is proposed to enable a more targeted approach to outburst prevention.