Chemical Reaction Effect on MHD Jeffery Fluid Flow over a Stretching Sheet Through Porous Media with Heat Generation/Absorption

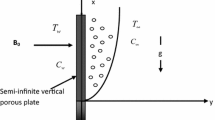
Abstract

The combined effect of heat and mass transfer in Jeffrey fluid flow through porous medium over a stretching sheet subject to transverse magnetic field in the presence of heat source/sink has been studied in this paper. The surface temperature and concentration are assumed to be of the power law form. The linear Darcy model takes care of the flow through saturated porous medium with uniform porosity. Further, first order chemical reaction rate has been considered to account for the effect of the reactive species, exhibiting non-Newtonian behaviour of Jeffery fluid model. Moreover, the present study analyses the result of previous authors’ as a particular case. The present work warrants attention to analytical method of solution by applying confluent Hypergeometric function and the fluid model considered here represents fluids of common interest such as solvent and polymers with zero shear-rate. The method of solution involves similarity transformation. The coupled non-linear partial differential equations representing momentum, concentration and non homogeneous heat equation are reduced into a set of non-linear ordinary differential equations. The transformed equations are solved by applying Kummer’s function. The effect of pertinent parameters characterizing the flow has been presented through the graph. Contributions of elasticity of the fluid, magnetic field and the porous matrix resist the motion of Jeffery fluid resulting a thinner boundary layer where as magnetic field and porous matrix contribute to enhance the temperature distribution in the flow domain.

Appendix

The new equation obtained from a differential equation by the confluence of two or more of its singularities is called the confluent equation of original equation. After confluence, the singularities of the new equation usually have properties more complicated than those of original ones; it follows that the properties are different. According to theory of differential equation only the singularities of differential equation could be the singularities of its solution.

The equation

$$\begin{aligned} z\left( 1-\frac{z}{b}\right) \frac{d^{2}y}{dz^{2}} +\left[ \gamma -(\alpha +\beta +1) \frac{z}{b}\right] \frac{dy}{dz}-\alpha \frac{\beta }{b}y=0 \end{aligned}$$

The singularities of the above equation are $0,b,\infty$ all being regular. Now let $b=\beta \rightarrow \infty$ we obtain

$$\begin{aligned} z\frac{d^{2}y}{dz^{2}}+[\gamma -z]\frac{dy}{dz}-\alpha y=0 \end{aligned}$$

This new confluent hypergeometric equation (Kummer’s equation) has only two singularities $0 \hbox { and } \infty$; the former is still a regular singularity, but the latter, being the confluence of two original regular singularity, becomes an irregular singularity. The Kummer’s function $F(\alpha ,\gamma ,z)$ is a single valued analytic function in the whole Z-plane whose properties are different from hypergeometric function $F( \alpha ,\beta ,\gamma ,z)$.

Further, solution of Kummer’s function depends upon roots of the indicial equation i.e. $\rho =0 \hbox { and } 1-\gamma$, when $1- \gamma$ is not an integer we obtain two linear independent solutions known as confluent hypergeometric function also known as Kummer’s function.

When $\gamma$ is an integer, sign of $\gamma$ will decide only one solution among the earlier two i.e. for $1-\gamma$ is not an integer. Another solution or the second solution can be obtained independently by other method.

The integral representation of Kummer’s function is as follows

$$\begin{aligned} F(\alpha ,\gamma ,z)=\frac{\Gamma (\gamma )}{\Gamma (\alpha )\Gamma (\gamma -\alpha )}\mathop {\int }\limits _0^1 {e^{zt}t^{\alpha -1}} (1-t)^{\gamma -\alpha -1}dt \end{aligned}$$

where $\hbox {Re}(\gamma )>\hbox {Re}(\alpha )>0, \arg (t)=\arg (1-t)=0$.

The integral representation, though comparatively simple, are rather restricted in its parameters $\alpha \hbox { and } \gamma$.

These are the limitations of Kummer’s function.