On the Nonlinear Vibrations of Polymer Nanocomposite Rectangular Plates Reinforced by Graphene Nanoplatelets: A Unified Higher-Order Shear Deformable Model

Abstract

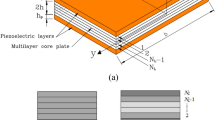
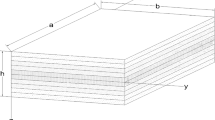
This paper presents a unified higher-order shear deformable plate model to numerically examine the nonlinear vibration behavior of thick and moderately thick polymer nanocomposite rectangular plates reinforced by graphene platelets (GPLs). Four distribution patterns of graphene nanoplatelet nanofillers across the plate thickness are considered. The effective material properties of graphene platelet-reinforced polymer (GPL-RP) nanocomposite plate are approximately calculated by employing the modified Halpin–Tsai model and rule of mixture. Using a generalized displacement field, a unified mathematical formulation is derived based on Hamilton’s principle in conjunction with von Kármán geometrical nonlinearity. By selecting appropriate shape functions, the proposed unified nonlinear plate model can be reduced to that on the basis of Mindlin, Reddy, parabolic, trigonometric and exponential shear deformation plate theories. The investigation of nonlinear vibration behavior is performed by employing a multistep numerical solution approach. In this regard, the discretization process is done through the generalized differential quadrature method. Then, the discretized governing equations are solved by employing the numerical-based Galerkin technique, periodic time differential operators and pseudo-arc length continuation algorithm. A detailed parametric study is carried out to examine the effect of GPL distribution pattern, weight fraction, geometry of GPL nanofillers and boundary constraints on the nonlinear vibration characteristics of the GPL-RP nanocomposite rectangular plates.

Appendices

Appendix 1

Definition

If A is an m-by-n matrix and B is a p-by-q matrix, the Kronecker product ${\mathbf{A}} \otimes {\mathbf{B}}$ is an mp-by-nq block matrix and defined as

$${\mathbf{A}} \otimes {\mathbf{B}}=\left[{\begin{array}{*{20}c}{a_{11} {\mathbf{B}}} &\cdots& {a_{1n} {\mathbf{B}}}\\ \vdots&\ddots&\vdots \\{a_{m1} {\mathbf{B}}} &\cdots& {a_{mn} {\mathbf{B}}}\\ \end{array}} \right]_{mp \times nq}$$

(b) Integral Matrix Operators

$$\mathop \int \limits_{{x_{1}}}^{{x_{N}}} f\left(x \right)dx=\left({\mathop \sum \limits_{r=0}^{N - 1} {\tilde{\mathbf{X}}}^{\left(r \right)} {\mathbf{D}}_{x}^{\left(r \right)}} \right){\mathbf{F}}={\mathbf{S}}_{x} {\mathbf{F}},\,{\mathbf{S}}_{x}= \left[{S_{x}} \right]_{1 \times N}$$

where ${\mathbf{D}}_{x}^{\left(r \right)}$ denotes the GDQ differential operator, and

$$\begin{aligned} {\tilde{\mathbf{X}}}^{\left(r \right)}&= \left[{\frac{{\left({x_{2}- x_{1}} \right)^{r + 1}}}{{2^{r + 1} \left({r + 1} \right)!}}, \ldots,\frac{{\left({x_{i + 1}- x_{i}} \right)^{r + 1}- \left({x_{i - 1}- x_{i}} \right)^{r + 1}}}{{2^{r + 1} \left({r + 1} \right)!}}, \ldots, - \frac{{\left({x_{N - 1}- x_{N}} \right)^{r + 1}}}{{2^{r + 1} \left({r + 1} \right)!}}} \right], \\ & \quad \quad \quad& \quad \quad \quad& \quad \quad \quad& \quad \quad \quad i=2,3, \ldots,N - 1 \\\end{aligned}$$

Appendix 2

The discretized components of K_ij, M_ij and ${\mathbf{K}}_{nl} \left({\mathbf{X}} \right)$ are as

$$\begin{aligned} {\mathbf{K}}_{11}&= A_{11} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}+ A_{66} {\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}},{\mathbf{K}}_{12}= \left({A_{12}+ A_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}, \\{\mathbf{K}}_{13}&= B_{11} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(3 \right)}+ \left({B_{12}+ 2B_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}, \\{\mathbf{K}}_{14}&= C_{11} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}+ C_{66} {\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}},{\mathbf{K}}_{15}= \left({C_{12}+ C_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}, \\{\mathbf{K}}_{21}&= \left({A_{12}+ A_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)},\quad{\mathbf{K}}_{22}= A_{22} {\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}}+ A_{66} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}, \\{\mathbf{K}}_{23}&= \left({B_{12}+ 2B_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}+ B_{22} {\mathbf{D}}_{{x_{2}}}^{\left(3 \right)}\otimes {\mathbf{I}}_{{x_{1}}},{\mathbf{K}}_{24}= \left({C_{12}+ C_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)},\\{\mathbf{K}}_{25}&= C_{22} {\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}}+ C_{66} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)},{\mathbf{K}}_{31}=- B_{11} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(3 \right)}- \left({2B_{66}+ B_{12}} \right){\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}, \\{\mathbf{K}}_{32}&=- B_{22} {\mathbf{D}}_{{x_{2}}}^{\left(3 \right)}\otimes {\mathbf{I}}_{{x_{1}}}- \left({B_{12}+ 2B_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}, \\{\mathbf{K}}_{33}&= A_{55} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}+ A_{44} {\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}}- D_{11} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(4 \right)}- 2\left({D_{12}+ 2D_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}- D_{22} {\mathbf{D}}_{{x_{2}}}^{\left(4 \right)}\otimes {\mathbf{I}}_{{x_{1}}}, \\{\mathbf{K}}_{34}&= A_{55} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}+ F_{11} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(3 \right)}+ \left({F_{12}+ 2F_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)},\\{\mathbf{K}}_{35}&= A_{44} {\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}+ \left({F_{12}+ 2F_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}+ F_{22} {\mathbf{D}}_{{x_{2}}}^{\left(3 \right)}\otimes {\mathbf{I}}_{{x_{1}}}, \\{\mathbf{K}}_{41}&= C_{11} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}+ C_{66} {\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}} {\mathbf{K}}_{42}= \left({C_{12}+ C_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}, \\{\mathbf{K}}_{43}&=- A_{55} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}+ F_{11} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(3 \right)}+ \left({F_{12}+ 2F_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}, \\{\mathbf{K}}_{44}&= H_{11} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}- A_{55} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{I}}_{{x_{1}}}+ H_{66} {\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}},{\mathbf{K}}_{45}= \left({H_{12}+ H_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}, \\{\mathbf{K}}_{51}&= \left({C_{12}+ C_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)},{\mathbf{K}}_{52}= C_{22} {\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}}+ C_{66} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}, \\{\mathbf{K}}_{53}&=- A_{44} {\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}+ \left({F_{12}+ 2F_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}+ F_{22} {\mathbf{D}}_{{x_{2}}}^{\left(3 \right)}\otimes {\mathbf{I}}_{{x_{1}}}, \\{\mathbf{K}}_{54}&= \left({H_{12}+ H_{66}} \right){\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)},{\mathbf{K}}_{55}= H_{22} {\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}}+ H_{66} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}- A_{44} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{I}}_{{x_{1}}}. \\\end{aligned}$$

(46)

$$\begin{aligned} {\mathbf{M}}_{11}&= {\mathbf{M}}_{22}= I_{0} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{I}}_{{x_{1}}},{\mathbf{M}}_{33}= I_{0} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{I}}_{{x_{1}}}- I_{4} \left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}+ {\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right), \\{\mathbf{M}}_{44}&= {\mathbf{M}}_{55}= I_{5} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{I}}_{{x_{1}}}.{\mathbf{M}}_{14}= {\mathbf{M}}_{41}= {\mathbf{M}}_{25}= {\mathbf{M}}_{52}= \varvec{I}_{2} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{I}}_{{x_{1}}},{\mathbf{M}}_{13}=- {\mathbf{M}}_{31}= I_{1} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}, \\{\mathbf{M}}_{23}&=- {\mathbf{M}}_{32}= I_{1} {\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}},{\mathbf{M}}_{34}=- {\mathbf{M}}_{43}=- I_{3} {\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)},{\mathbf{M}}_{35}=- {\mathbf{M}}_{53}=- I_{3} {\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}, \\\end{aligned}$$

(47)

Also, one can be written the components of the nonlinear stiffness vector as follows

$$\begin{aligned} {\mathbf{K}}_{{u_{1}}} \left({\mathbf{X}} \right) &= A_{11} \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}} \right){\mathbf{w}}} \right) + \left({A_{12}+ A_{66}} \right)\left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \\ & \quad+ A_{66} \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}} \right){\mathbf{w}}} \right), \\{\mathbf{K}}_{{u_{2}}} \left({\mathbf{X}} \right) &= A_{22} \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right) + \left({A_{12}+ A_{66}} \right)\left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \\ & \quad+ A_{66} \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right), \\{\mathbf{K}}_{w} \left({\mathbf{X}} \right) &= \left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right)\left({{\mathbf{N}}_{11}\circ \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right)} \right) + \left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right)\left({{\mathbf{N}}_{22}\circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right)} \right) \\ & \quad+ \left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right)\left({{\mathbf{N}}_{12}\circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right)} \right) + \left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right)\left({{\mathbf{N}}_{12}\circ \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right)} \right) \\ & \quad- B_{11} \left({\left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}} \right){\mathbf{w}}} \right) + \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(3 \right)}} \right){\mathbf{w}}} \right)} \right) \\ & \quad- \left({B_{12}+ 2B_{66}} \right)\left({\left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) + \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}} \right){\mathbf{w}}} \right)} \right) \\ & \quad- B_{66} \left({\left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right) + \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right)} \right) \\ & \quad- B_{12} \left({\left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) + \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right)} \right) \\ & \quad- B_{22} \left({\left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right) + \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(3 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right)} \right), \\{\mathbf{K}}_{{\psi_{1}}} \left({\mathbf{X}} \right) &= C_{11} \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{\varvec{x}_{1}}}^{\left(2 \right)}} \right){\mathbf{w}}} \right) + \left({C_{12}+ C_{66}} \right)\left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \\ & \quad+ C_{66} \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}} \right){\mathbf{w}}} \right), \\\end{aligned}$$

$$\begin{aligned} {\mathbf{K}}_{{\psi_{2}}} \left({\mathbf{X}} \right)=C_{22} \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right) + \left({C_{12}+ C_{66}} \right)\left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + C_{66} \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right). \hfill \\\end{aligned}$$

(48)

where

$$\begin{aligned} {\mathbf{N}}_{11}&= A_{11} \left[{\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{u}}_{1}+ \frac{1}{2}\left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right)} \right] \\ & \quad+ A_{12} \left[{\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{u}}_{2}+ \frac{1}{2}\left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right)} \right] + C_{11} \left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\varvec{\uppsi}}_{1}\\ & \quad+ C_{12} \left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\varvec{\uppsi}}_{2}+ B_{11} \left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}} \right){\mathbf{w}} + B_{22} \left({{\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}, \\{\mathbf{N}}_{22}&= A_{22} \left[{\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{u}}_{2}+ \frac{1}{2}\left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right)} \right] \\ & \quad+ A_{12} \left[{\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{u}}_{1}+ \frac{1}{2}\left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right)} \right] + C_{22} \left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\varvec{\uppsi}}_{2}\\ & \quad+ C_{12} \left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\varvec{\uppsi}}_{1}+ B_{22} \left({{\mathbf{D}}_{{x_{2}}}^{\left(2 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}} + {\text{B}}_{12} \left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(2 \right)}} \right){\mathbf{w}}, \\{\mathbf{N}}_{12}&= A_{66} \left[{\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{u}}_{1}+ \left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{u}}_{2}+ \left({\left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right) \circ \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\mathbf{w}}} \right)} \right] \\ & \quad+ C_{66} \left[{\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\varvec{\uppsi}}_{1}+ \left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\varvec{\uppsi}}_{2}} \right] \\ & \quad+ B_{66} \left({\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{I}}_{{x_{1}}}} \right){\varvec{\uppsi}}_{1}+ \left({{\mathbf{I}}_{{x_{2}}}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\varvec{\uppsi}}_{2}+ 2\left({{\mathbf{D}}_{{x_{2}}}^{\left(1 \right)}\otimes {\mathbf{D}}_{{x_{1}}}^{\left(1 \right)}} \right){\mathbf{w}}} \right). \\\end{aligned}$$

(49)

where ${\mathbf{I}}_{{x_{1}}}$ and ${\mathbf{I}}_{{x_{2}}}$ are, respectively, N × N and M × M identity tensors and ° indicates the Hadamard product.