1 Introduction

Highly precise products with close tolerances are manufactured by non-conventional machining methods in aerospace and defence industries. Specifically, electric discharge machining (EDM) is practically versatile applications of non-conventional machining in precision manufacturing industries to manufacture precise and close tolerance parts with higher accuracy. Therefore, it is the requirement that regular estimations should be made to measure the form tolerances [1,2,3,4,– 5].

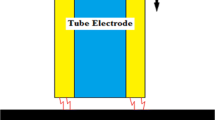
The schematic of the EDM is illustrated in Fig. 1. When a suitable voltage is supplied across the cathode (tool) and anode (workpiece), an electrostatic field of high strength is established which cause emission of an electron from the tool. The emitted electrons get accelerated towards workpiece and collide with the dielectric fields molecules, breaking them into electrons and ions [6, 7]. The produced electrons accelerate and dislodge. As a result, a spark is produced between anode and cathode and a very high temperature is developed on the electrode. The high temperature causes melting and vaporization of the material. EDM is used to manufacture precise and difficult- to- machine materials such as superalloys [8,9,10].

Fig. 1
figure 1

Schematic of electric discharge machining (EDM)

Full size image

Nickel-based superalloys are extensively used in high precision components because of its excellent properties [11,12,13]. However, based on the properties Inconel 625 is a well identified difficult-to-machine superalloy [14]. Inconel 625 wrought superalloy has a high cutting temperature due to its lesser thermal conductivity and specific heat. Furthermore, built-up edge (BUE) engrave at the tip of the tool, when this super-alloy is machined by using traditional machining processes. Therefore, EDM has been explored for the machining of this superalloy by using copper and brass electrodes [15).

Various researchers have been reported work on EDM to measure the influence of input parameters on performance parameters. As an attempt to use the EDM process effectively, researchers reported the dominance of EDM parameters in hole drilling of nickel-based superalloy [16].

Narender Singh presented multiple performance characteristics optimizations for EDM constraints by applying the Taguchi based Grey relational Analysis method (GRA) for AL-10% SiC composites. Li demonstrated the application of grey-fuzzy logic based orthogonal array (OA) for optimization [15].

Form Tolerance may be described as the deviation between the maximal and minimal limits and the total measure that a particular dimension is allowed to deviate. Tolerances are specified generally by two methods; unilateral tolerance and the bilateral tolerance. Unilateral tolerance allows the variance for a nominal measure in one direction only, whereas the bilateral tolerance allows the dimensional variation in both the directions from the specified value [2, 17, 18].

Specification of Cylindricity/Circularity Tolerance is the condition of a cylindrical and cone surface in which entire points of the intersected surface by the plane perpendicular to an axis are at equal distance from that axis. It is a geometric tolerance that restrains the radial difference between the highest and lowest points in an element. It never uses a datum feature reference and can only be applied to a circular cross-section (i.e. sphere, cylinder, cone etc.). Tolerances for circular shape elements are lobbying, ovality and irregular shape. Circularity is a perfect condition & it results in perfect circular elements. However, the perfect conditions cannot be developed, therefore, it’s essential to determine the tolerance for deviation from circularity. Cylindricity is the circumstance of a surface rotation where all levels of the surface are at equal distance from the common axis. It never uses a datum reference and can only be applied to a single cylindrical element. Cylindricity tolerance is the deviation permitted on a cylindrical surface. Cylindricity tolerance zone is the length between two axial cylinders & this distance is equalising to the tolerance value 8, 10, 19, 20] (Fig. 2).

Fig. 2
figure 2

Test for a standard-compliant circularity/cylindricity specification

Full size image

Stanislaw [8] investigated the importance of cylindricity measurement by using the reference method. Adamczak presented the principle of reference method and also presented the method for comparing the cylindrical profile [22, 23] measured and analyzed the cylindricity, diameter, roundness, straightness and taper for EDM micro-holes by using coordinate measuring machine (CMM). Therefore, the importance of form tolerance in manufacture components was discussed.

Volkan Yilmaz and Murat Sarikaya et al. [24,25,26] optimized the EDM performance parameters namely machining rate, WR (wear rate), AOC (average over-cut) and taper angle by using Taguchi, RSM, Regression analysis and ANNs (artificial neural networks) for µ-EDD (Electrical discharge drilling) of AISI-304 SS and Hand field steel. The authors concluded that discharge current had the most significance on performance parameters. Guren Meral et al. [27] statistically optimized the Ra value, torque and thrust force for two drill geometries on AISI-4140 using Taguchi based GRA method.

Some researchers have been reported the use of different shape Cu electrodes and multihole electrodes to predict the machinability in the EDM process [28,29,30,31,32,33,34,35,36,37,38,39]. Wl-Taweel [28] concluded that the Al-Cu-Si-TiC powder sintered electrodes are more sensitive to Ton (pulse on time) and peak current. Khan [29] demonstrated the effect of Cu and brass electrodes to measure electrode wear and MRR (material removal rate) during EDM of Al and mild steel. The author concluded that the Cu electrode has a low wear rate and highest MRR as compared to the brass electrode. The wear rate increases with the increase in both voltage and current. Kin et al. [35] concluded that the machinability of Cu electrode is higher and the bigger DIA. Of multihole electrode reduces the MRR. Govindan and Murugesan et al. [36, 37] investigated and optimized the EDM parameters by GRA method using multihole electrodes.

From the literature survey, it is ascertained that no plausible works were reported to measure form tolerances such as cylindricity and circularity on an Inconel-718 Ni-based superalloy using a different diameter circular shape multi-hole copper electrode in EDM process. Therefore, this experimental analysis and multi-objective optimization work being undertaken to improve the form tolerances in EDM by Taguchi analysis, Fuzzy logic and GRA method.

2 Experimental setup

Design-of-experiments (DoE) needs cautions scheduling, practical layout of the trials, Taguchi has identical procedures for every DoE application steps and the DoE can dramatically decrease the number of trials [21, 40] Thus, the four major process constraints viz. Hole DIA. Of multi-hole electrode, Peak current (Ip), pulse on time (Ton) and dielectric fluid pressure had selected for the governing parameter, and each parametric quantity had three levels, as designated in Table 1.

Table 1 Allocated values of EDM constraints and their levels
Full size table

Bruker SI turbo Analyzer and Hardness Tester HT-7 were used to measure the chemical composition and the hardness values of Inconel-718 plate. As per DoE (design of experiment), the experiments were performed on 15 amps rated die-sinking SPARONIX-EDM. The different diameters of multi-holes were engraved by laser drilling. The EDM set-up and different diameters multi-hole copper electrodes used for experimentation are shown in Fig. 3a, b.

Fig. 3
figure 3

a Experimental set-up of die sinking SPARKONIX-EDM; b Different DIA, multi-hole Cu electrodes

Full size image

The Inconel-718 workpiece was used in the form of a 4 mm thick rectangular plate. The workpiece and the electrodes were linked up with +ve and –ve polarity in the D.C. power source, respectively. Die-electric kerosene along with various pressure ranges was used with centre flushing technique for the experimental work. The weight of the electrodes and workpiece was measured before and after machining for every trial run with digital weight-balance (up to 0.001-g accuracy).

The mathematical relation used to evaluate the material removal rate (MRR) is given in Eq. 1.

$$ \text{MRR} = \frac{{\text{Weight of work material removal }}}{{\text{Time}}}\;\left( {g/\hbox{min} } \right) $$
(1)

The mathematical relation used to calculate the electrode wear rate (EWR) is given below in Eq. 2.

$$ \text{EWR} = \frac{{\text{Weight of electrode material removal }}}{{\text{Time}}}\;\left( {g/\hbox{min} } \right) $$
(2)

Each trial was evaluated thrice and the mean values were obtained. The form tolerances namely cylindricity and circularity were measured by using a TESA Micro-Hite 3D co-ordinate measuring machine (CMM).

3 Form tolerance analysis

The aim of this experimental analysis is to increase the MRR and to minimize the value of form tolerances namely cylindricity and circularity. In the present experimentation work, L9 (3**4) orthogonal array (OA) was chosen. This OA has 9 constraints combinations, therefore; the total numbers of 9 experiments were conducted to measure the interactions between the various factors. The parameter combinations using the L9 OA are expressed in Table 2.

Table 2 DOE matrix of L9 orthogonal array (OA)
Full size table

For accurate measurements minimum, three values were taken for each specimen and the mean value was selected. The mean values of the MRR, EWR and form tolerances such as circularity and cylindricity are shown in Table 3.

Table 3 Measured values for output responses using circular profile multi-hole Cu electrode, as per DOE
Full size table

3.1 Taguchi analysis of circular profile multi-hole Cu electrode

Taguchi analysis is used for the selection of best-optimized parameter value for the individual process parameter and to measure the influence of each parameter at different levels.

3.1.1 Dominance of input constraints on MRR

The ANOVA main effect plot for data means shows the effect of an individual parameter at a different level of MRR. For the measurement of MRR, larger is better (S/N) was utilized because the maximum value of MRR means the higher rate of production. Therefore, for the measurement of MRR, ‘Larger is better’ ratio is used.

The MRR value is maximum at the level-2 of Elec. Hole DIA., level-3 of (Ip), level-3 of (Ton) and level-2 of dielectric fluid pressure, as givenn in Table 4. Therefore, these are the best-optimized values of parameters for MRR. The rank is given as 1, 2 3 & 4 in Table 5 shows the most influencing parameters for MRR. For MRR, peak current (Ip) and dielectric fluid pressure is the most influencing constraint, whereas the Ton and DIA. of an electrode has the least significance.

Table 4 ANOVA response table (MRR)
Full size table
Table 5 Levels of selected input variables at maximum MRR
Full size table

The influence on MRR in relation to changes in input variables is presented in Fig. 4.

Fig. 4
figure 4

Dominance on MRR in relation to change of process constraints a Ip and dielectric fluid pressure; b Ton and Toff

Full size image

3.1.2 Influence of input constraints on EWR

The ANOVA main effect plot for data means indicate the effect of an individual parameter at a different level of EWR (electrode wear rate). For the measurement of EWR, Smaller is better (S/N) was utilized because the minimum value of EWR means the higher accuracy of production and tool life. Therefore, for the measurement of EWR, ‘Smaller is better’ ratio is used.

From the main effect for data means the EWR is minimum at the 3rd level of DIA. of the multi-hole electrode, 2nd level of Ip, 2nd level of Ton and 3rd level of dielectric fluid pressure, as given in Table 7. Therefore, these are the best-optimized values of parameters for EWR. The rank is given as 1, 2 3 & 4 in Table 6 shows the most influencing parameters for EWR. For EWR, Ton is the most dominating constraint whereas the DIA. of the multi-hole electrode has the least significance.

Table 6 ANOVA response table (EWR)
Full size table
Table 7 Levels of selected input variables at minimum EWR
Full size table

The influence on EWR in relation to changes in input variables is illustrated in Fig. 5.

Fig. 5
figure 5

Influence on EWR in relation to change of process constraints a Elec. Multi-hole diameter and dielectric fluid pressure; b Ip and Ton

Full size image

3.1.3 Dominance of input parameters on circularity

The ANOVA main effect plot presents the effect of an individual parameter at the different level of form tolerance namely circularity. For the measurement of circularity, smaller is better (S/N) was utilized because the minimum value of circularity deviation means the higher precision and accuracy. Therefore, for the measurement of circularity, ‘Smaller is better’ ratio is used.

From the main effect for data means the circularity form tolerance is minimum at the 1st level of DIA. of the multi-hole electrode, 2nd level of Ip, 2nd level of Ton and 1st level of dielectric fluid pressure, as given in Table 8. Therefore, these are the best-optimized values of parameters for circularity. Dielectric fluid pressure and Ip are the most influencing constraint for circularity, whereas the DIA. of multi-hole electrode and Ton has the least significance, as shown in Table 9.

Table 8 ANOVA response table (circularity)
Full size table
Table 9 Levels of selected input variables for circularity
Full size table

The influence on circularity in relation to changes in input variables is presented in Fig. 6.

Fig. 6
figure 6

Influence on Circularity in relation to change of process constraints a Elec. Multi-hole DIA. and dielectric fluid pressure; b Ip and Ton

Full size image

3.1.4 Dominance of input parameters on cylindricity

The ANOVA main effect plot is showing the effect of an individual parameter at a different level of Cylindricity tolerance. For the measurement of cylindricity form tolerance, smaller is better (S/N) ratio was used because the minimum value of cylindricity deviation means the highest precision and accuracy. Therefore, for the measurement of cylindricity, ‘Smaller is better’ ratio is used.

From the main effect for data means, cylindricity form tolerance is minimum at the 3rd level of DIA. of the multi-hole electrode, 2nd level of Ip, 3rd level of Ton and 1st level of dielectric fluid pressure, as given in Tables 10 and 11. Therefore, these are the best-optimized values of parameters for cylindricity. Dielectric fluid pressure and DIA. of Multihole electrode are the most influencing parameter for cylindricity, whereas the Ton and IP have less significance.

Table 10 ANOVA response table (cylindricity)
Full size table
Table 11 Levels of selected input variables for cylindricity
Full size table

The influence on Circularity in relation to change of variables is presented in Fig. 7.

Fig. 7
figure 7

Influence on Cylindricity in relation to change of a Ip and dielectric fluid pressure; b Ton and Elec. Multi-hole DIA

Full size image

4 Multi-parametric optimization using the Grey relational method

The steps used for multi-parametric optimization using the Grey relational analysis are discussed below [40, 41]:

(a) Normalization of the all experimental results of MRR, EWR, Machining Time and form tolerances such as the angle and flatness: Linear normalization of experimental values is performed in the range of 0 and 1. The normalized values for output responses were calculated by using the standard formula:

$$ \text{Normalized results }(X_{ij} ) = \frac{{(y_{ij} ) - (\min_{j} y_{ij} )}}{{(\max_{j} y_{ij} ) - \left( {\min_{ij} y_{ij} } \right)}} $$
(3)

where yij = ith experiment results in jth experiment.

(b) Calculation for the Grey relational coefficients:

Grey relational coefficients are evaluated to express the relation between the ideal and factual experimental consequences. The standard formula used for the computation of Grey relational coefficients is given below:

$$ \delta_{ij} = \frac{{\min_{i} \min_{j} \left| {x^\circ_{i} - x_{ij} } \right| + \xi \max_{i} \max_{j} \left| {x^\circ_{i} - x_{ij} } \right|}}{{\left| {x^\circ_{i} - x_{ij} } \right| + \xi \max_{i} \max_{i} \left| {x^\circ_{i} - x_{j} } \right|}}, \;0 < \xi < 1 $$
(4)

where \({x^\circ_{i} - x_{i} }\) =  ideal normalized result.

(c) Calculation for the Grey relational grade:

Grey relational grades as shown in Table 12 are evaluated by the average of Grey relational coefficient using the formula given below:

$$ \upalpha_{j} = \frac{1}{m}\mathop \sum \limits_{i = 1}^{m}\updelta_{ij} $$
(5)

where

  • αj = Grey relational grade

  • m = No. of execution grade characteristics.

Table 12 Calculated values for normalization, Grey relational coefficient and grades
Full size table

(d) Calculation of the optimum levels: optimum levels are calculated to find the significant parameters as shown in Table 13.

Table 13 Grey relational grade response table
Full size table

(e) Selection of the optimal levels of process parameters by taking the highest values of levels for each parameter from the optimum level table. The Response table is clearly indicating the level values for process parameters. The highest value of process parameters for each parameter showed the best-optimized value.

(f) Confirmation of experiment and verification of the optimized process parameters.

4.1 Confirmation of experiment

After obtaining the optimized values of process parameters the last step is to confirm the experimentation as shown in Table 14.

Table 14 Confirmation of experiment
Full size table

The estimated Grey relational grade can be calculated from the following given relation:

$$ \widehat{\upalpha} = \alpha_{m} + \mathop \sum \limits_{i = 1}^{q} \left( {{\bar{\alpha }}_{i} -\upalpha_{m} } \right) $$
(6)

where αm = Total mean of the Grey relational grade at optimum level, q = No. of process parameters.

5 Fuzzy logic modelling for performance predictions

For Fuzzyfication, the triangular-shaped function was used to describe the input variables and trimf- shaped functions were practised for output variables. ‘Trimf (triangular MF’s) is frequently used because this function has inclined and decline features with one certain value’. Three trimf MF’s were used for each variable as input, namely Low (L), Medium (M) and High (H) and five trimf MF’s were used for the output variables (MRR, EWR and form tolerance) namely Very Low (VL), Low (L), Average (Avg.), Good and Excellent. The linguistic variables and fuzzy expressions are mentioned in Table 15. The MF’s for fuzzy-set input are engraved hole diameter of Multi-hole electrode (D), Peak current (Ip), Pulse on Time (Ton) and dielectric fluid pressure whereas the membership functions of fuzzy set output (MRR, EWR and form tolerance) are shown in Fig. 8

Table 15 Selected linguistic variables for fuzzy model
Full size table
Fig. 8
figure 8

Trimf MF’s for Input and output variables (fuzzy-logic designer)

Full size image

5.1 Structure of fuzzy rules

The Fuzzy rules as illustrated in Fig. 9 were built based on the actual observational results and a set of 9 rules were constructed as given below:

  1. 1.

    If (Electrode hole DIA. is Small) and (Ip is L) and (Ton is L) and (Dielectric fluid pressure is L) then (MRR is VL) (EWR is H) and (Circularity is Avg.) and (Cylindricity is Avg.).

  2. 2.

    If (Electrode hole DIA. is Small) and (Ip is M) and (Ton is M) and (Dielectric fluid pressure is Avg.) then (MRR is Good) (EWR is Avg.) and (Circularity is VL) and (Cylindricity is VL).

  3. 3.

    If (Electrode hole DIA. is Small) and (Ip is H) and (Ton is H) and (Dielectric fluid pressure is H) then (MRR is Excellent) (EWR is Avg.) and (Circularity is L) and (Cylindricity is H).

  4. 4.

    If (Electrode hole DIA. is M) and (Ip is L) and (Ton is M) and (Dielectric fluid pressure is H) then (MRR is Avg.) (EWR is L) and (Circularity is L) and (Cylindricity is VH).

  5. 5.

    If (Electrode hole DIA. is M) and (Ip is M) and (Ton is H) and (Dielectric fluid pressure is L) then (MRR is Good) (EWR is L) and (Circularity is VL) and (Cylindricity is VL).

  6. 6.

    If (Electrode hole DIA. is M) and (Ip is H) and (Ton is M) and (Dielectric fluid pressure is Avg.) then (MRR is Excellent) (EWR is VH) and (Circularity is L) and (Cylindricity is Avg.).

  7. 7.

    If (Electrode hole DIA. is Large) and (Ip is L) and (Ton is H) and (Dielectric fluid pressure is Avg.) then (MRR is Avg.) (EWR is L) and (Circularity is VH) and (Cylindricity is VL).

  8. 8.

    If (Electrode hole DIA. is Large) and (Ip is M) and (Ton is L) and (Dielectric fluid pressure is H) then (MRR is Avg.) (EWR is L) and (Circularity is L) and (Cylindricity is Avg.).

  9. 9.

    If (Electrode hole DIA. is Large) and (Ip is H) and (Ton is M) and (Dielectric fluid pressure is L) then (MRR is Avg.) (EWR is L) and (Circularity is VL) and (Cylindricity is VL).

Fig. 9
figure 9

Trimf MF’s for Input and output variables

Full size image

Mamdani Fuzzy logic was used to simulate the experimental results as shown in Fig. 10. The obtained results are explained herewith:

Fig. 10
figure 10

Influence on output responses in relation to change of input variables (fuzzy model)

Full size image

5.2 Accuracy of fuzzy model’s

To measure the Fuzzy model accuracy, as shown in Fig. 11, the predicted values were calculated by using the fuzzy model and keeping the same set of input values. Error and Accuracy of the model are measured by the following relations:

$$ e_{i } = \left( {\frac{{\left| {H_{m} - H_{p} } \right|}}{{H_{m} }} } \right) \times 100 \% $$
(7)

where \( \varvec{e}_{{\varvec{i }}} \) = individual error, \( \varvec{H}_{\varvec{m}} \) = measured value and \( \varvec{H}_{\varvec{p}} \) = predicted value.

Fig. 11
figure 11

Comparison of fuzzy logic model with experimental results

Full size image

Accuracy is the closeness of predicted value to the measured value. The accuracy and error for Fuzzy model are shown in Table 16. The mathematical relation used to calculate the accuracy is given below:

Table 16 Comparison of Fuzzy model and experimental results
Full size table
$$ A = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left( {1 - \frac{{\left| {H_{m} - H_{p} } \right|}}{{H_{m} }} } \right) \times 100 \% $$
(8)

where A = accuracy of the model and N = number of experiments.

6 Results and conclusion

The EDM process parameter for Ni-based superalloy (Inconel-718) has been optimized by Taguchi analysis and multi-objective optimization method GRA to obtain an optimal solution. The optimized parameters for the response of MRR, EWR and form tolerance are: Ø 0.16 mm DIA. of the multi-hole electrode, 8 Amps Ip, 600 µs Ton and 0.1 kg/m2 dielectric fluid pressure. The optimal solutions have been calculated from output responses. An attempt has also been made to attain the Max. and Min. Evaluation of MRR and form tolerances respectively. The attained outcomes had also been examined through a real experiment and established to be satisfactory. The experimental results showed considerable advancement in the process. From Taguchi analysis, the obtained results are: For MRR, Ip and dielectric fluid pressure are the most significant constraints, whereas the Toff has the least significance. The MRR improves with an increase in spark discharge area which is higher for the multihole electrode. For EWR, DIA. of a hole in the multihole electrode is the most influencing parameters, whereas the Ton has the least significance. Ton and Ip are the most influencing constraint for circularity, whereas the DIA. of the multi-hole electrode has less significance. For cylindricity form tolerance, Dielectric fluid pressure is the most influencing parameter, whereas the Ton has less significance.

The utilization of a multi-hole electrode improves the MRR as well as the form tolerances and minimizes the EWR. The Fuzzy model has been developed to measure the output results. The accuracy and percentage of the model is 96.45% respectively. This model may be used to predict the accurate output responses (MRR, EWR and form tolerance) of Ni-based superalloy. The attained optimal outcomes had been tested by conducting a real experiment trial and found to be acceptable. Therefore, these experimental results will facilitate the aerospace and defence industries to improve the productivity, performance and MRR of Inconel-718 superalloy with closer tolerances.