1 Introduction

With the advent of micro and nano-technology, several industries investigated on researches of small-sized products. Consequently, micro and nano-electro-mechanical-systems (M/NEMS) have been widely introduced to the scientific and engineering society. MEMS is basically introduced on the modeling, mechanical analysis, simulation and microfabrication steps. Final product of MEMS includes such wide applications including: small-sized sensors, actuators, resonators, gyroscopes, accelerometers etc. each one of the examples has their own specific application in diverse engineering products. MEMS is a field of highly inter-disciplinary studies between mechanical, electrical, chemical and bio-medical engineering. As mentioned, MEMS gyroscopes are amongst the most practical devices applicable in Automotive and imaging industries. In inertial navigation systems (INS) of advanced cars, MEMS gyroscopes in conjunction with steering wheel sensors can be utilized to prevent roll-over of the car. Such MEMS elements can also be used within a car airbag. In advanced imaging devices industry, MEMS gyroscopes are applied in order to diminish the blurring effect due to unwanted motions of the camera. Consequently, optimized and proper design of MEMS gyroscopes deals with increasing car safety along with quality of imaging machines. To design efficient elements, modeling is the first step and one the most commonly-used models is small-sized rod. In order to capture size-dependencies, non-classical theorems should be used instead of classical continuum mechanics theorem. One of such non-classical theories is the non-local elasticity theory (NLET) [1,2,3,4,5]. This theory is basically established based on the assumption that in small-sized elements; stress at a point is not only a function of the strain at that point, but it is also dependent on the strain of the points at the vicinity. This theory is divided into integral-based and differentiation-based cases.

There are several researches available, in which the static and dynamic analysis of M/NEMS has been done. Ghanbari and Babaei [6] studied the new boundary condition effects upon dynamic analysis of a micro-cantilever. Shaat [7] investigated the slowly varying waves analysis based on the nonlocal theory revealing the approximations of the non-local theory. Zenkour [8] used a mixed theory mostly using non-local assumptions to peruse the thermo-elastic vibration behavior of nano-plates. Babaei et al. [9] studied dynamic behavior of functionally graded beam exposed to thermal stresses. They have pictured the effects of shear deformations especially useful for thick beams. Dynamic-vibration analysis of a micro-beam is reported by Babaei et al. [10]. Ghanbari et al. [11] used a numerical method to study the vibration analysis of a beam under inertia effects at random points along the length of the beam. Sahmani and Aghdam [12] studied postbuckling analysis of functionally graded composite size-dependent plate reinforced with GPLs based on non-local strain gradient theory. Nonlinear vibrations of functionally graded plate based on non-local strain gradient theory is reported by Sahmani et al. [13]. Sahmani et al. [14] reported nonlinear bending analysis of functionally graded beam reinforced one with graphene platelets. Sahmani and Fattahi [15] reported nonlinear instability of shear deformable cylindrical nano-panels which is subject to axial compression and thermal stresses.

Besides to the non-classical theories, here is a brief literature review about the analysis of small-sized rods. Longitudinal vibration analysis of rods based on the non-local strain gradient theory is reported by Zhu and Li [16]. Sumelka et al. [17] carried out the free longitudinal vibration behavior of a nonlocal rod. They utilized the fractional continuum mechanics theory. Static and dynamic stability of an elastic rod embedded on a nonlinear base is studied by Annin et al. [18]. Mei et al. [19] presented dynamic and vibration analysis of a vibrating rod which has variations along the length direction. They used diverse rod theories to derive the equations. Li and Liu [20] carried out a research regarding vibration analysis and active control of piezoelectric structure. They proposed spectral element structure method through the analysis of the rod. Abrate [21] studied the vibration analysis of non-uniform beams and rods based on analytical and Rayleigh–Ritz methods. Rahmani and Rahman [22] worked on controlling concept of a MEMS gyroscope. Rahmani and Rahman [23] also extended their research on adaptive and sliding control of a MEMS gyroscope. Rahmani et al. [24] carried out a research about PID control of a MEMS gyroscope model using bat algorithms. Rahmani [25] reported MEMS gyroscope control using robust control concepts.

There is a complementary notion to conceive the rod rotating around a fixed axis. This is especially efficient for small-sized gyroscopes. Along with this notion, rotation effect in terms of rotation velocity upon frequencies of the system is to be investigated. Stiffening effects on dynamic characteristics of rotating beams is reported by Kim et al. [26]. Ghafarian and Ariaei [27] carried out a research regarding vibration behavior of a system of interconnected Timoshenko beams capturing rotating effects. Using iteration method, Chen et al. [28] conducted a research about vibration analysis of tapered beams. Kiani [29] studied vibration analysis of a tapered wire based on the non-local theory and perturbation technique. Simsek [30] conducted a research about vibration behavior of a rod with gradations along the length.

Constraint between the axial displacement and rotational displacement is an optimized idea firstly introduced by Babaei and Yang [31]. They proposed a coupled linear displacement field for the first time to analyze the dynamic-vibration behavior of a uniform nano-rod model of a MEMS gyroscope. This optimized model is rotating around a fixed axis with various velocities. However, to present a more comprehensive gyroscope model, non-uniformity and axial gradations of the rod are being considered as well. In other words, to the best of my knowledge, there is not any published technical paper addressing the rotation effects upon dynamic analysis of a tapered (axially functionally graded) nano-rod based on the coupled displacement fields. In short, for the first time; axial vibration analysis of clamped–clamped and clamped-free, rotating tapered (geometrically non-uniform) rod is reported based on both classical and non-local theories along with an optimized concept to capture both translational and rotational rates.

2 Preliminaries of non-local theory

Eringen [5] assumed the following equation as the nonlocal characteristic equation:

$$\uplambda \upvarepsilon _{\text{rr}} \left[ {1 - \mu^{2} \nabla^{2} } \right]{\text{t}}_{\text{kl}} =\updelta_{\text{kl}} +\upmu \upvarepsilon _{\text{kl}}$$
(1)

Assumptions of classic continuum mechanics state that in an elastic medium stress field at a random point \(x\) is a function of the strain field of that very random point. Eringen has nullified this single-dependency and expressed that for small-sized systems, stress field of the desired point is a function of the strain field of all points existing within the configuration. In Eq. (1), \({\text{t}}_{\text{kl}}\) is nonlocal stress tensor, \(\upvarepsilon_{\text{kl}}\) is strain tensor, \(\uplambda\) and \(\upmu\) represent Lame’s constants. \(\mu^{2}\) is nonlocal parameter which consists of \({\text{e}}_{0}\) and \(a\) (\(\mu = {\text{e}}_{0} a\)), wherein \({\text{e}}_{0}\) is a quantity which varies from material to material, and \({\text{a}}\) is the internal characteristic length of each material. Constitutive relation based on nonlocal theory is:

$$\upsigma_{\text{xx}} - \mu^{2} \frac{{\partial^{2}\upsigma_{\text{xx}} }}{{\partial {\text{x}}^{2} }} = {\text{E}}\upvarepsilon_{\text{xx}}$$
(2)

In Eq. (2), \(\upsigma_{\text{xx}}\) and \(\upvarepsilon_{\text{xx}}\) represent axial normal stress and axial normal strain. \(\upsigma_{\text{xz}}\) shows shear stress, and \(\upgamma_{\text{xz}}\) is shear strain. \({\text{E}}\) and \({\text{G}}\) are modulus of elasticity and rigidity (\({\text{G}} = {\text{E}}/2\left( {1 +\upnu} \right)\)), \(\upnu\) is Poison’s ratio). In Eq. (2), putting nonlocal parameter equal to zero yields constitutive relation of a classic model.

3 Mathematical modeling

3.1 Kinematic relations

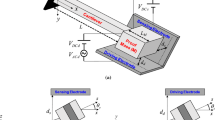
Consider a non-uniform rod with length \(L\), and radius \(r\) of cross section area \(A_{0}\). Length of the beam is aligned with \(x\) axis coordinates and show in (Fig. 1).

Fig. 1
figure 1

Schematic of tapered rotating rod (a clamped-free), (b clamped–clamped)

Full size image

Axially functionally graded rod has taper shape (Fig. 2). This non-uniformity causes the gradation of area along the \(x\) direction which finally makes rod stiffness variable.

Fig. 2
figure 2

Schematic of tapered rod

Full size image

Using Thales theorem, \(r\left( x \right)\) is obtained in terms of base radius (\(r_{0}\)), \(x\) and \(L\):

$$r\left( x \right) = r_{0} \left( {1 - \frac{x}{L}} \right)$$
(3a)

Expectedly cross section area of the rod is \(x\)-dependent at each specific point:

$$A\left( x \right) = \pi r\left( x \right)^{2} = \pi r_{0}^{2} \left( {1 - \frac{x}{L}} \right)^{2}$$
(3b)

Considering area of the base cross section as \(A_{0} = \pi r_{0}^{2}\), Eq. (3b) can be converted to the following equation:

$$A\left( x \right) = A_{0} \left( {1 - \frac{x}{L}} \right)^{2}$$
(3c)

It is good to consider the case where, radius is increasing along \(x\) direction. In this case, Eq. (3c) is converted to Eq. (3d):

$$A\left( x \right) = A_{0} \left( {1 + \frac{x}{L}} \right)^{2}$$
(3d)

In the case of longitudinal vibrations, displacement along the \(x\) plane does not play any roles; however displacement along the length is the major point:

$$u_{x} \left( {x,t} \right) = u\left( {x,t} \right)$$
(4a)
$$u_{y} = u_{z} = 0$$
(4b)

where \(t\) shows time. There is only one non-zero strain term:

$$\varepsilon_{xx} = \frac{{\partial u\left( {x,t} \right)}}{\partial x}$$
(5)

In this section, coupled displacement field is defined. Rod is rotating around a fixed axis shown by \(z\) axis. Based on a novel concept, rotational displacement of the rod is supposed to be a linear proportional function of rod translational axial displacement (Babaei and Yang [31]). In details, this concept states that rotation of the rod at each specific point of the infinitesimal element times length of the element \(x\) is a multiple of the axial displacement of the element. In other words, length of the arc passed through rotation is equal to a multiple of axial displacement.

$$x\theta \left( t \right) = pu\left( {x,t} \right)$$
(6)

In Eq. (6), \(p\) is velocity factor.

3.2 Strain potential and kinetic energy terms

In this case study, there are two major energy terms influential through behavior if the system. Because of the elongations and axial displacements, potential energy due to normal axial strain is to be considered. It is good to note that, lateral strain terms in comparison to axial strain terms are discounted. Strain potential energy of the rod can defied as following equation:

$${\text{U}}_{s} = \frac{1}{2}\mathop \int \limits_{\text{V}} {\text{E}}\left( {\frac{{\partial {\text{u}}\left( {{\text{x}},{\text{t}}} \right)}}{{\partial {\text{x}}}}} \right)^{2} {\text{dV}}$$
(7)

In Eq. (7) \({\text{V}}\) shows the volume of the rod.

Kinetic energy term encompasses the energy of bulk of the rod due to axial displacements and definite kinetic energy due to rotation.

$$T = \frac{1}{2}I_{o} \left( {\frac{{\partial\uptheta\left( {\text{t}} \right)}}{{\partial {\text{t}}}}} \right)^{2} + \frac{1}{2}\mathop \int \limits_{0}^{L}\uprho{\text{A}}\left( {\text{x}} \right)\left( {\frac{{\partial {\text{u}}\left( {{\text{x}},{\text{t}}} \right)}}{{\partial {\text{t}}}}} \right)^{2} {\text{dx }}$$
(8)

where \(A\) is area of cross section, \(\rho\) is density, and \(I_{o}\) is the second moment of mass inertia around the fixed axis, which can be written as:

$$I_{o} = \int x^{2} dm$$
(9)

dm represents the mass of the infinitesimal element of the rod.

Substituting Eq. (9) into Eq. (8) leads to the following:

$$T = \frac{1}{2}\int x^{2} \left( {\frac{{\partial\uptheta\left( {\text{t}} \right)}}{{\partial {\text{t}}}}} \right)^{2} dm + \frac{1}{2}\mathop \int \limits_{0}^{L}\uprho{\text{A}}\left( {\frac{{\partial {\text{u}}\left( {{\text{x}},{\text{t}}} \right)}}{{\partial {\text{t}}}}} \right)^{2} {\text{dx }}$$
(10)

In Eq. (10) rotational displacement (\(\theta\)) is only function of time and using Eq. (6) both integrands can be accreted into a single one:

$$T = \frac{1}{2}\left( {p^{2} + 1} \right)\mathop \int \limits_{0}^{L}\uprho{\text{A}}\left( {\text{x}} \right)\left( {\frac{{\partial {\text{u}}\left( {{\text{x}},{\text{t}}} \right)}}{{\partial {\text{t}}}}} \right)^{2} {\text{dx }}$$
(11)

3.3 Hamilton’s principle

In order to derive the dynamic-vibration equations of the tapered rotating rod based on non-local theory (NLET); Hamilton’s variational approach is adopted. Based on this approach, variations of a system through quite short time interval is equal to zero. To follow this approach, variations of energy terms are obtained:

$$\delta T = \left( {p^{2} + 1} \right)\mathop \int \limits_{0}^{L}\uprho{\text{A}}\frac{{\partial {\text{u}}}}{{\partial {\text{t}}}}\frac{\partial }{\partial t}\delta t dx$$
(12)
$$\delta U_{s} = \mathop \int \limits_{V}\upsigma_{xx} \delta \varepsilon_{xx} dV$$
(13)

where \(\upsigma_{xx} = E\varepsilon_{xx}\);

Introduction of the stress resultant (N) leads to the modified form of Eq. (13):

$$N = \mathop \int \limits_{A}\upsigma_{xx} dA$$
(14)

Using Eq. (14) and concept of variational approach, variations of strain energy is shown in Eq. (15):

$$\delta U_{s} = \mathop \int \limits_{0}^{L} {\text{N}}\delta \varepsilon_{xx} dx$$
(15)

In mathematical language, Hamilton’s principle implies the following equation:

$$\mathop \int \limits_{{t_{1} }}^{{t_{2} }} \delta Lag = 0$$
(16)

where \(Lag\) is Lagrangian and defined as:

$$Lag = T - U_{s}$$
(17)

Substituting Eqs. (12) and (15) into Eq. (17) and applying the integration over time interval (Eq. (16)); combination of variational terms are obtained as integrand. The mentioned integral can lead to the dynamic-vibration equation of the tapered rotating rod using integration by parts:

$$\left( {p^{2} + 1} \right)\uprho{\text{A}}\left( {\text{x}} \right)\frac{{\partial^{2} {\text{u}}\left( {{\text{x}},{\text{t}}} \right)}}{{\partial {\text{t}}^{2} }} - \frac{\partial N}{\partial x} = 0$$
(18)

Equation (18) includes stress resultant. To find the mentioned equation explicitly in terms of translational terms; some mathematical operations are required: first of all, integrating Eq. (2) over area, and using Eq. (17) leads to the following auxiliary equation:

$$N - \mu^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}N = EA\left( x \right)\frac{{\partial u\left( {x,t} \right)}}{\partial x}$$
(19)

Second derivative of stress resultant out of Eq. (18) can be replaced with the equivalent term in Eq. (18):

$$N = \left( {p^{2} + 1} \right)\mu^{2} \left( {\uprho{\text{A}}\left( {\text{x}} \right)\frac{{\partial^{3} {\text{u}}\left( {{\text{x}},{\text{t}}} \right)}}{{\partial {\text{x}}\partial {\text{t}}^{2} }}} \right) + EA\left( x \right)\frac{{\partial u\left( {x,t} \right)}}{\partial x}$$
(20)

Now, first derivative of the above equation with respect to stress resultant and substituting into Eq. (18) leads to the following equation which is explicitly expressed in terms of the desired parameters:

$$\left( {1 - \left( {p^{2} + 1} \right)\mu^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right)\left( {\uprho{\text{A}}\left( {\text{x}} \right)\frac{{\partial^{2} {\text{u}}\left( {{\text{x}},{\text{t}}} \right)}}{{\partial {\text{t}}^{2} }}} \right) = \frac{\partial }{\partial x}\left( {EA\left( x \right)\frac{{\partial u\left( {x,t} \right)}}{\partial x}} \right)$$
(21)

Boundary conditions of the clamped–clamped rod is:

$$\left. u \right|_{x = 0,L} = 0$$
(22)

Boundary conditions for the clamped-free rod is:

$$\left. u \right|_{x = 0} = 0,\quad \left. {\frac{\partial u}{\partial x}} \right|_{x = L} = 0$$
(23)

4 Solution method

4.1 Non-dimensioning procedure

Since the presented model is considered under free vibrations, and with no viscous damping effect, displacement function can be stated as:

$$u\left( {x,t } \right) = U\left( x \right){ \exp }\left( {i\omega t} \right)$$
(24)

where \(\omega\) represents natural frequency of vibrations, \(i^{2} = - 1\), and \(U\left( x \right)\) is axial displacement function. Substituting Eq. (24) into Eq. (21) yields the following ordinary differential equation:

$$\left( {p^{2} + 1} \right)\omega^{2} \left( {1 - \mu^{2} \frac{{d^{2} }}{{dx^{2} }}} \right)\left( {\uprho{\text{A}}\left( {\text{x}} \right)U\left( x \right)} \right) + \frac{d}{dx}\left( {EA\left( x \right)\frac{dU\left( x \right)}{dx}} \right) = 0$$
(25)

Using following parameters, Eq. (25) is changeable into a non-dimensional equation (Eq. (26)):

$$\Omega = \omega L\sqrt {\frac{\rho }{E}} ,\quad \zeta = \frac{x}{L},\quad \gamma = \frac{\mu }{L}$$
$$\left( {p^{2} + 1} \right)\Omega ^{2} \left( {1 - \gamma^{2} \frac{{d^{2} }}{{d\zeta^{2} }}} \right)\left( {\uprho{\text{A}}\left( \zeta \right)U\left( \zeta \right)} \right) + \frac{d}{d\zeta }\left( {EA\left( \zeta \right)\frac{dU\left( \zeta \right)}{d\zeta }} \right) = 0$$
(26)

Expanding Eq. (26) results in:

$$\Omega ^{2} U\left( \zeta \right)A\left( \zeta \right) -\Omega ^{2} \gamma^{2} A\left( \zeta \right)\frac{{d^{2} U\left( \zeta \right)}}{{d\zeta^{2} }} - 2\Omega ^{2} \gamma^{2} \frac{dA\left( \zeta \right)}{d\zeta }\frac{dU\left( \zeta \right)}{d\zeta } -\Omega ^{2} \gamma^{2} U\left( \zeta \right)\frac{{d^{2} A\left( \zeta \right)}}{{d\zeta^{2} }} + \frac{dA\left( \zeta \right)}{d\zeta }\frac{dU\left( \zeta \right)}{d\zeta } + A\left( \zeta \right)\frac{{d^{2} U\left( \zeta \right)}}{{d\zeta^{2} }} = 0$$
(27)

Equation (27) can be rewritten in the following form:

$$\left( {1 - \left( {p^{2} + 1} \right)\Omega ^{2} \gamma^{2} } \right)A\left( \zeta \right)\frac{{d^{2} U\left( \zeta \right)}}{{d\zeta^{2} }} + \left( {1 - 2\left( {p^{2} + 1} \right)\Omega ^{2} \gamma^{2} } \right)\left( {\frac{dA\left( \zeta \right)}{d\zeta }\frac{dU\left( \zeta \right)}{d\zeta }} \right) + \left( {p^{2} + 1} \right)\Omega ^{2} \left( {A - \gamma^{2} \frac{{d^{2} A\left( \zeta \right)}}{{d\zeta^{2} }}} \right)U\left( \zeta \right) = 0$$
(28)

Equation (28) is the non-dimensional from of dynamic-vibration equation of tapered rotating non-local rod.

4.2 Rayleigh–Ritz method

By non-dimensioning the governing equation, it is easier to solve it. To solve Eq. (28), Rayleigh–Ritz method is adopted. Based on this approximate method, \(U\left( \zeta \right)\) can be replaced with expansion series including comparison functions satisfying natural boundary conditions of the system. It is good to note that, comparison functions satisfy the natural boundary conditions of any system. Such functions are inferior to admissible functions when the system has forced boundary conditions. Since in this case, we face only natural boundary conditions, comparison functions work well. For the clamped-clamed rod, sine-based functions and for the clamped-free boundary conditions, cosine-based functions are suggested.

$$f_{i} \left( \zeta \right) = { \sin }\left( {\frac{i\pi }{L}\zeta } \right)$$
(29)
$$f_{i} \left( \zeta \right) = { \cos }\left( {\frac{i\pi }{L}\zeta } \right)$$
(30)

Mentioned admissible functions should be multiplied by unknown coefficients to form the expansion series:

$$U\left( \zeta \right) = \mathop \sum \limits_{i = 1}^{n} c_{i} f_{i} \left( \zeta \right)$$
(31)

Substitution of the proposed mode shape functions into Eq. (28) yields the following equation:

$$\left( {1 - \left( {p^{2} + 1} \right)\Omega ^{2} \gamma^{2} } \right)A\left( \zeta \right)\frac{{d^{2} }}{{d\zeta^{2} }}\mathop \sum \limits_{i = 1}^{n} c_{i} f_{i} \left( \zeta \right) + \left( {1 - 2\left( {p^{2} + 1} \right)\Omega ^{2} \gamma^{2} } \right)\left( {\frac{dA\left( \zeta \right)}{d\zeta }\frac{d}{d\zeta }\mathop \sum \limits_{i = 1}^{n} c_{i} f_{i} \left( \zeta \right)} \right) + \left( {p^{2} + 1} \right)\Omega ^{2} \left( {A - \gamma^{2} \frac{{d^{2} A\left( \zeta \right)}}{{d\zeta^{2} }}} \right)\mathop \sum \limits_{i = 1}^{n} c_{i} f_{i} \left( \zeta \right) = 0$$
(32)

Since there is not any external forces, viscous dampers and dissipating forces; Rayleigh’s quotient can be applied through solution procedure since this principle concerns the maximum kinetic and maximum potential energies of a system in the absence of dissipating and external forces. Using this quotient, a continuous (lumped) system is discretized into a discrete system with \(n\) degrees of freedom. Number of degrees of freedom is adoptable by number of comparison (admissible) functions we consider. Based on Rayleigh–Ritz, minimizing the Rayleigh’s quotient with respect to the unknown coefficients converts differential Eigen-value problem into algebraic Eigen-value problem which yields non-dimensional frequencies of the system by solving the homogenous algebraic Eigen-value problem using MATLAB.

5 Results and discussion

In this paper; free vibrations of rotating, tapered and non-local rods based on two common boundary conditions of clamped–clamped and clamped-free is studied. It is good to mention that taking \(\alpha\) equal to zero, yields uniform rod, putting \(\gamma\) equal to zero results in classical rod, and neglecting angular velocity factor (\(p = 0\)) leads into fixed rod. Firstly, to verify the presented model along with the suggested solution procedure, Tables 1, 2, 3, 4, 5 and 6 are provided. Since the problem of this paper is a comprehensive analysis including rotation effect, non-uniformity (taper) effect, and non-local effect; different technical references are presented to verify each effect. In details; Tables 1 and 2 verify the present results based on Rayleigh–Ritz method of fixed, uniform, and classical rods with other papers. Tables 3 and 4 show the evaluation of present results of fixed, tapered, and classical rods with Abrate [21] Finally, Tables 5 and 6 demonstrate good level of result accuracy of fixed, uniform, and non-local rods with technical references.

Table 1 Comparison of first three modes of vibration of fixed uniform and classical clamped-free rod \((\gamma = 0,\;p = 0,\;\alpha = 0)\)
Full size table
Table 2 Comparison of first three modes of vibration of fixed uniform and classical clamped–clamped rod \((\gamma = 0,\;p = 0,\;\alpha = 0)\)
Full size table
Table 3 Comparison of first three modes of vibration of fixed tapered and classical clamped-free rod \((\gamma = 0,\;p = 0,\;\alpha \ne 0)\)
Full size table
Table 4 Comparison of first three modes of vibration of fixed tapered and classical clamped–clamped rod \((\gamma = 0,\;p = 0,\;\alpha \ne 0)\)
Full size table
Table 5 Comparison of first three modes of vibration of fixed uniform and non-local clamped-free rod \((\gamma \ne 0,\;p = 0,\;\alpha = 0)\)
Full size table
Table 6 Comparison of first three modes of vibration of fixed uniform and non-local clamped–clamped rod \((\gamma \ne 0,\;p = 0,\;\alpha = 0)\)
Full size table

In order to obtain specific effects of: gradation along the length better known as the non-uniformity (taper parameter \(\alpha\)), size-dependency (\(\gamma\)), and coupled rod rotations (angular velocity factor \(p\)); following eight figures are presented solely for each parameter:

Figure 3 shows fundamental natural frequency changes of a classical non-uniform, increasing-cross section rod based on different values of angular velocity factor. As the taper parameter increases, frequencies of clamped-free rod decrease; in contrast, frequencies of clamped–clamped rod increase. For clamped-free rod; Frequency decrement is pretty sharp when \(\alpha < 2\), gentle variations happen when \(2 < \alpha < 5\) and finally variations are comparatively insignificant if \(\alpha > 5\). For clamped–clamped rod; variations are gentle almost for all values of taper parameter.

Fig. 3
figure 3

Variations of non-dimensional frequency with increasing taper parameter (a clamped-free, b clamped–clamped)

Full size image

Figure 4 demonstrates the effects of taper parameter of an increasing-cross section non-uniform rod. Increment of taper parameter results in increment of the frequency. To make the analysis physically meaningful; for an increasing-cross section tapered rod, taper parameter is limited to interval of \(0 < \alpha < 1\). For both clamped-free and clamped–clamped rods; frequency increases by increment in the value of \(\alpha\). Such increments are steep for clamped–clamped rod and gentle for the clamped–clamped rod. Another finding yields the fact that for clamped–clamped rod, variations are sharper if \(< 0.5\).

Fig. 4
figure 4

Variations of non-dimensional frequency with decreasing taper parameter (a clamped-free, b clamped–clamped)

Full size image

Figure 5 shows results of fixed, non-local decreasing-cross section rod. Accordingly; for a clamped-free rod, frequency decreases as taper parameter increases. However for clamped–clamped rod, quite small variations take place by increment of taper parameter and frequencies increase slightly. An eye-catching point is the existence of a chaotic behavior for a clamped-free rod. This sudden drop-down (plunge) happens when \(1 < \alpha < 2\) and \(\gamma = 1\). Accordingly; as non-local parameter is enhanced in value frequency reaches zero faster, initial sharp decrements gets more gentle, and finally when non-local parameter passes specific value, behavior of the system totally changes and frequency increases to the acme point. At the acme point there is a sudden plunge resulting in no vibrations. For clamped–clamped rod, smooth and quite slight increments take place by increasing taper parameter.

Fig. 5
figure 5

Variations of non-dimensional frequency with increasing taper parameter (a clamped-free, b clamped–clamped)

Full size image

Variations for fixed, non-local decreasing-cross section rod are illustrated in Fig. 6. For both clamped-free and clamped–clamped rods; frequencies increase as the taper parameter gets greater. And this is valid for all values of non-local parameter. For clamped-free rod, variations are more inclined upwards in comparison to the clamped–clamped rod. When \(\alpha > 0.5\) clamped-free rod behaves more oscillatory. So expectedly, more oscillations happen if taper parameter is greater and this fact is true regardless of non-local parameter.

Fig. 6
figure 6

Variations of non-dimensional frequency with decreasing taper effect (a clamped-free, b clamped–clamped)

Full size image

Variations of frequency for classical rotating non-uniform rod are reported in Fig. 7. Vibration frequencies of both clamped–clamped and clamped-free rods diminish by increasing the angular velocity. Sharpest drop-down is observed when \(p < 10\), mediocre variations appear if \(10 < p < 30\), finally system behaves with pretty small and insignificant oscillations whenever rotation rates are great (\(p > 30\)). Feature of Fig. 7 discloses the fact that; in contrast to the above-shown figures, boundary conditions do not play a chief role when variations are essentially based on angular velocity factor (Fig. 8).

Fig. 7
figure 7

Variations of non-dimensional frequency with velocity for different vales of increasing taper parameter (a clamped-free, b clamped–clamped)

Full size image
Fig. 8
figure 8

Variations of non-dimensional frequency with velocity for different values of decreasing taper parameter (a clamped-free, b clamped–clamped)

Full size image

Figure 7 shows results based on the increasing-cross section tapered rod; similar results are shown when cross section area of the axially functionally graded rod is decreasing. Similarly, vibrations dwindle as system rotates at higher rates and the same regime mentioned above for \(p\) is valid here. It is also valuable to note that for decreasing-cross section rod, boundary condition type is not a key factor and behavior changes of the system is independent of boundary conditions unless the specific values of frequencies are dependent on boundary conditions for all cases.

Figure 9 illustrates the chaotic behavior of fixed, non-local, tapered rod with increasing cross-section area. In details; for clamped-free rod as non-local parameter increases for some values of taper parameter, frequency decreases and for some other values frequency increases. For small values of taper parameter, increment of non-local parameter leads to decrement in frequency. This decrement gradually inflects when taper parameter increases. In other words, enhancing the effect of area variations along the length, effects of non-local parameter are suppressed by taper parameter. Starting from \(\alpha = 1\), frequency values are inflected from decline into rise, as a result it is technically safe to note that for the values of taper and non-local parameter specified in Fig. 9; non-uniformity overcomes influences of non-locality. This chaotic behavior emerges more significantly whenever \(0.5 < \gamma < 0.5\) and \(\alpha = 5\); frequency increases up to the acme point. At the acme point there is sudden harsh plunge and dropdown to zero. For clamped–clamped case, increment of non-local parameter leads to higher frequency values and for all cases of taper parameter, frequency rate is certainly negative. In this case, chaos appears in the content of frequency value. Meaning that enhancing taper and non-local effects, leads into no detectable pattern to determine whether frequency is increasing or decreasing. For example, comparison of \(\alpha = 1\) and \(\alpha = 5\) reveals that for some values of \(\gamma\) the more taper effect, the higher frequency. In contrast, for some other \(\gamma\) values, the more taper effect, the smaller frequency. Keeping increment in \(\gamma\) inflects the results again. Consequently, it is not feasible to come up with specific pattern(s) for the mentioned case. And the only certain point is the decrement of frequency with non-local effect.

Fig. 9
figure 9

Variations of non-dimensional frequency with non-local effect for different values of increasing taper parameter (a clamped-free, b clamped–clamped)

Full size image

Figure 10 shows behavior of fixed, non-uniform (decreasing-cross section of area), non-local rod. For clamped–clamped rod, there is a neat pattern certifying the decrement of frequency with intensifying the non-locality. For the clamped–clamped case, the very chaos mentioned for the increasing-cross section non-uniformity takes place. Comparison of two different values of taper effect (\(\alpha = 1\) and \(\alpha = 5\)) accompanied by increasing non-local parameter, yields no specific patterns. The only finding from this figure testifies decrement of frequency with intensifying the non-locality.

Fig. 10
figure 10

Variations of non-dimensional frequency with non-local effect for different values of decreasing taper parameter (a clamped-free, b clamped–clamped)

Full size image

6 Conclusion

In this technical paper, free longitudinal vibration analysis of clamped-free (CF) and clamped–clamped (CC) tapered rod is studied. This nano-rod model represents schematic of MEMS gyroscope. For the first time, incorporated effects of: size dependency parameter (non-local parameter), coupled angular motions (angular velocity factor), and taper parameter (non-uniformity) over frequencies of the system are studied in details. To derive the governing equations of motion, Hamilton’s variational approach is being used. Rayleigh–Ritz numerical method is utilized to solve the derived equations. Main findings of this study are: taper parameter intensifies vibration frequencies for all cases and boundary conditions except when cross-section area of a CF rod is increasing. In the mentioned sole case, increment of taper parameter results in decreased rate of vibrations. There is a case where effects of taper parameter gradually vanish and the system behaves almost independently. This condition occurs when the cross-section area of a CC rod is increasing and rod is intensely highly non-uniform. Making the system rotate faster always suppresses vibrations and this is valid for all types of boundary conditions and area changes types. Incorporation of taper parameter along with non-local parameter shows the outcomes mentioned above; however there is a chaos taking place for the sole case (increasing-cross section CF rod) meaning that no specific patterns could be captured. In this case, enhancing non-uniformity accompanied with small and mediocre values of non-local parameter shows diminishing rate of oscillations. This pattern keeps alive up to critical values of the taper parameter and non-local factor. By reaching such critical values, chaos takes place and system starts to oscillate intensely with severe rise followed by a plunge and reaching static state implying suppressed vibrations case. Second chaotic behavior of the system is observed when CC rod has either type of cross-section area changes (increasing and decreasing). Intensifying non-local effect yields slight oscillations, however incorporation of taper parameter makes it indiscernible how the vibration rates diminish. In short; behavior analysis of tapered, non-local, rotating rod system is totally influenced by non-uniformity, non-locality, and rotations velocity as well as boundary conditions. This means that such systems conduct predictable and sometimes chaotic and unpredictable manners. In other words, design of micro-gyroscopes with such complexities requires comprehensive and case-by-case analysis of material, geometrical and velocity-based factors. Such an optimized design will result in better performance of gyroscopes with less car roll-overs, higher safety and more accurate cameras along with other advantages in other industrial applications.