1 Introduction

The scratch test is a quasi-non-destructive method, was developed [1, 2] over 2 decades ago, made up of pushing a tool across the surface of a weaker rock and tracing the groove at a given penetration depth. The uniaxial or unconfined compressive rock strength (\({\text{UCS}}\)) which is the ultimate stress a rock can withstand before undergoing failure, is characterized by rock confining pressure, stress–strain relationship, and pore-fluid pressure. Analysis and prediction of the in situ rock failure behavior as a function of rock type, pore pressure, spatio-temporal stresses, and fault-reactivation potential provides critical information for proactive decision-making to achieve successful energy production operations.

In the optimization of hydrocarbon exploitation, hydraulic fracturing has proven to be one of the most efficient matrix stimulation methods in unconventional reservoirs [3, 4]. During this treatment, complex fracture networks are often generated, and the interaction of hydraulic and natural fractures significantly influences the complexity of the fracture networks created [5, 6]. Stronger rocks will exhibit greater fracture toughness \((K_{IC} )\), which will influence the fracture geometry and propagation. UCS, \(K_{IC}\), and other rock mechanical parameters influencing how the fracture nucleates [7], fracture size and geometry, but fracture sizes and geometry adopted in hydraulic fracture design and modelling, Discrete Fracture Network (DFN) modeling, and Finite Element Modeling (FEM); are most often overestimated. Although scratch tests are applicable nowadays to several fields of science and engineering, ranging from strength characterization of rocks and cements/ceramics [8, 9], to damage of polymers [10,11,12] and metals [13, 14], and quality control of thin films and coatings [15, 16]; the underlying rock failure mechanisms, characterization, and applications has not been fully explored. Although several researchers have attempted to evaluate and quantify UCS, fracture toughness, and other rock mechanical properties in conventional and unconventional reservoir rocks using indentation and scratch testing methods, but there remain differing opinions on the fundamental approach and principles to be adopted in estimating those parameters.

Over the past decades of advances in the evaluation of geomechanical properties through scratch tests, prior to this our contribution, there still exists a gap in the state of knowledge of the scratch test method and its application to solve current needs of the energy industry. This paper discusses and summarizes the key findings regarding the use of scratch test method to estimate rock strength, fracture toughness, and other geomechanical properties over the past few decades. Firstly, we highlight the advantages of scratch testing method over other conventional methods of estimating geomechanical properties. Secondly, we extensively discussed the methodology, modifications, and its devices available in published research studies. Subsequently, we presented the application of scratch test to measure and estimate geomechanical properties. Lastly, we provided recommendations for future research to address identified outstanding problems related to the application of scratch test method to estimate geomechanical properties for improved hydrocarbon and geothermal exploitation and production, and geologic carbon sequestration.

2 The scratch test method

2.1 Scratch test method versus other conventional methods

The uniaxial compressive test using load frame to evaluate the \({\text{UCS}}\) of core plugs is one of the most popular methods. The indentation test [17] is another popular conventional method of estimating mechanical properties of rocks, and other materials. This method involves the use of a scratching tool to create indentations on the surface of the material surface. In a research study [18], micro-nano indentation method was utilized to evaluate and predict KIC in shale rocks, but the study failed to account for maximum holding stage on the indentation-displacement curves in fracture toughness estimation. This fracture toughness model deficiency was highlighted and corrected in Zeng et al. [19], but the final \(K_{IC}\) values are in the order of magnitude two. The macroscopic and mesoscopic rock mechanical parameters of shale rocks were investigated by authors in Chen et al. [20] using micro-indentation test method. The shale outcrops from the Cambrian Longmaxi formation in Sichuan Basin, China, was utilized for the study. In the results, the authors observed that mesoscopic elastic modulus and indentation hardness are heterogeneously distributed across the formation and exhibits a non-linear increase behavior with rise in packing density. The microscopic mechanical properties of shale rocks were not accounted for in this study.

The shale rock samples from the Longmaxi formation in Sichuan Basin, China, was utilized to estimate \(K_{IC}\) through micro-indentation method [21]. The authors aim to address the previous limitation of the \(K_{IC}\) estimation observed in Zeng et al. [19], and their results showed much lower \(K_{IC}\) values. In KIC measurement using indentation method, results are more of qualitative, and can yield high inaccuracy and subjectivity by virtue of the crack length measurement requiring optical imaging method, which is onerous task for non-translucent rocks like shale [22]. Other methods of estimating rock’s UCS include the point-load test [23, 24]; and “Drill Test” [25], which was developed using the drilling concept and incorporates 2/3 butt core sections to evaluate UCS in shale rocks.

The rebound hardness test method using EquotipR hardness tester [26, 27] was initially adopted for evaluating the UCS of rocks, but recently utilized for creating UCS logs and strength contrast profiles of shale rocks [28, 29]. The rebound hardness test can also be carried out using Schmidt hammer [30]. Although the rebound index test is also useful in qualitatively estimating the UCS of rocks, it has proven inefficient in providing a continuous and accurate quantitative rock strength profile [31]. This is another means the scratch test has proven its efficiency over other methods of testing rock strength by providing continuous high-resolution logs of rock strength with high degree of repeatability.

The effect of anisotropy in \(K_{IC}\) was estimated in Gokaraju et al. [32] using Chevron Bend (CB) test and Boundary Element Method model. Sierra et al. [33] also utilized the Chevron Notched Semicircular Bend (CNSCB) test to estimate rock strength and fracture toughness of Woodford shale rocks, with the estimated fracture toughness (\(K_{IC}\)) values in Lower and Middle Woodford shale much lesser than values of Upper Woodford shale. In a study by Chandler et al. [34] using a modified Short-Rod sample geometry to estimate anisotropic \(K_{IC}\) values of Mancos Shale rock, conflicting values were obtained in divider, short-transverse, and arrester configurations. Coring operation was also suggested as another viable method of estimating UCS from data obtained from acoustic and bulk density logs [35].

The advantages of scratch test method over other conventional methods discussed, to measure and estimate geomechanical properties are [36,37,38,39]:

  1. (a)

    It is quasi-non-destructive, and the post-test core samples remain intact which can be utilized for other destructive or non-destructive tests.

  2. (b)

    It provides direct equivalent measurement with the rock’s UCS.

  3. (c)

    It requires limited and minimal level of sample preparation.

  4. (d)

    It is simple, quick, and highly repeatable.

  5. (e)

    It can be conducted on any dimension of rock, as the results are not affected by the core sample geometry.

  6. (f)

    It provides precise continuous profile of rock strength over the scratch interval.

The scratch profile from the scratch tests provides a reliable quantitative measurement of the scale and distribution of the heterogenous properties along the tested core samples.

2.2 The mechanics of rock scratching

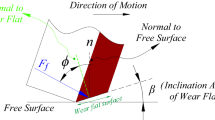
In the scratch testing method, continuous trace of the groove of the rock surface is conducted with a stronger cutting tool, while the cutter penetration depth (d) and the cutting velocity (v) between the cutter and the rock are held constant. In Fig. 1, the FT and FV are horizontal and vertical components of the cutting force (FC) applied on the cutter face, which is normal to the cutting velocity. The rock cutting configuration is also composed of other parameters such as: the back-rake angle of the cutter (θ); the contact surface between the cutter and the rock surface which is represented by \(l\); frictional force (Ff) acting on wear-flat surface below the cutter; cross-sectional area (Ac) of the cutter face; width (w) of the cutter; and the internal friction angle of the (∅).

Fig. 1
figure 1

Rock scratching configuration

Full size image

The mechanisms of rock scratching are evident in the linear relationship between cutter penetration depth (d) and \(F_{T}\). The two rock failure mechanisms (Fig. 2) depending on the cutter penetration depths are [40, 41]:

Fig. 2
figure 2

Modified from [55]

Schematic of rock failure regimes a Ductile regime; b Brittle regime.

Full size image
  1. (a)

    Ductile failure mode: Also known as “plastic flow”. The ductile failure mode occurring at shallow penetration depth (d), is characterized by the rock shearing ahead of the cutter. As the rock matrix and the grains are dislodged, the rock grains and powder accumulate continuously ahead of the cutter, and they are removed by the moving cutter.

  2. (b)

    Brittle failure mode also known as “chipping”, The brittle failure mode occurring at large penetration depth (d), is characterized by macroscopic fractures generating from the tip of the cutting tool and propagates upwards towards the rock surface ahead of the cutter. The chips and fragments formed are removed by the cutter.

The brittle failure mode is dependent on fracture toughness \((K_{IC} )\), while the ductile failure mode on \({\text{UCS}}\), and the transition between ductile and brittle failure modes is dependent on the cutter penetration depth (d).

He and Xu [42] adopted the Bažant’s Size Effect Law (SEL) to investigate the critical ductile-to-brittle transition depth in a wide range rock type. This critical ductile-to-brittle transition penetration depth \((d_{c} )\), distinguishes the ductile failure regime from the brittle failure regime. The Quasi-brittle fracture property of cement paste was investigated [7] to account for the linear elastic relationship between applied forces and scratch width and depth \((w\sqrt d )\). The authors proposed a linear scaling method from scratch geometrical scale to large scale ranges for estimating \(K_{IC}\) in homogenous materials.

2.3 Scratch test devices

2.3.1 The rock strength device

The Rock Strength Device (RSD) is designed to scratch the rock surface while the normal and tangential forces applied to the cutter are measured, and the device is kinematically controlled [2, 43,44,45]. The main components of the RSD as shown in Fig. 3 are: 1—a transverse with a core holder of length \(l\); 2—a moving cart; 3—housing the vertical positioning system; 4—the load cell; 5—cutting tool; 6—computer controlled stepper-motor (controls the horizontal movement of the cart); 7—horizontal ball screw; 8—gearbox; 9—the vertical positioning system (controls the depth of cut); 10—micrometer; 11—locking system (keeping the vertical mechanical system locked against the frame to maintain a constant penetration depth). The load sensor measures tangential \((F_{T} )\) and vertical \((F_{V} )\) forces acting on the cutter.

Fig. 3
figure 3

Rock strength device showing the front and side view [63]

Full size image

2.3.2 The wombat machine

The wombat scratch test machine as shown in Fig. 4, is a unique scratch test equipment developed by Epslog S.A. with the capability of testing core samples up to 3 ft long and a diameter range between 0.5 and 6 in. The following are the main components of the Wombat machine: horizontal bed on which the core samples are fixed; mobile carriage to hoist the vertically erected cutter; load sensor measuring \(F_{T}\) and \(F_{V}\); high-definition camera to capture continuous images of the rock core surface during scratching. The results are processed and analyzed by a computer software solution.

Fig. 4
figure 4

Wombat scratch machine (Image Courtesy of Epslog S.A.)

Full size image

2.3.3 Other devices

The Mechanical Profiler Test System (MPTS) from TerraTek TSI™ [46,47,48] is another type of scratch test equipment utilized for estimating rock mechanical properties and other parameters through the scratch test method. Its system consists of a moving cart containing a core sample holder, a cutting tool with the rock “scratching” capability, loading cell to measure the vertical and horizontal forces acting on the rock surface. As part of an existing compression machine, a simple scratching cell was developed [49] and utilized to create rock strength correlation for predicting \({\text{UCS}}\) of rocks in Saudi Arabia. Most recently, the miniature linear cutting device [50] was developed using a milling machine and designing it to measure forces and distance scratched by the probe.

3 Scratch test method application for estimation of geomechanical properties

3.1 Uniaxial compressive strength (UCS)

The scratch test can be resourceful in estimating reservoir geomechanical and petrophysical properties. The concept of obtaining rock strength information from rock cutting tests was proposed by Adachi et al. [51, 52], and this approach was dependent on phenomeno-logical model of continuously cutting of rock with blunt cutter. This cutter/rock interaction model in ductile failure mode was developed based on three assumptions, irrespective of the cutting tool wear. These assumptions are that [2, 40]: (i) the forces acting on the cutter face, averaged over a distance higher than the penetration depth, is directly proportional to the cross-sectional area \((A_{c} )\) due to horizontal force; (ii) the inclination of the average force acting normal to the cutter face is constant; (iii) friction force at the wear-flat rock interface exists. The above developed model is composed of three major parameters:

  1. (a)

    The intrinsic specific energy \((\varepsilon )\) of the rock cutting process, which is the energy required to cut rock per unit volume, and this parameter correlates to UCS.

  2. (b)

    The inclination \((\zeta )\) of the average force acting on the face of the cutter.

  3. (c)

    The coefficient of friction \((\mu )\) on the wear flat/rock interface.

The model assumptions and its application to estimate rock strength, combining the pure cutting and frictional contact process is presented in Eqs. 1–6 (assuming a rectangular cutter; Ac = wd) as:

$$F_{T} = \varepsilon \left( {1 - \mu \zeta } \right)wd + F_{V}$$
(1)
$$\mu = \tan \emptyset$$
(2)
$$E = E_{o} + \mu S$$
(3)
$$E = \frac{{F_{T} }}{wd}$$
(4)
$$S = \frac{{F_{V} }}{wd}$$
(5)
$$E_{o} = \varepsilon \left( {1 - \mu \zeta } \right)$$
(6)

where \(S\) is the drilling strength, and \(E\) is the specific energy.

The feasibility of RSD to estimate rock strength parameters from scratch test was first conducted [51]. The researchers used blunt and sharp cutters in conducting the scratch tests on sandstone samples. The RSD was also utilized [40] to investigate to estimate the rock strength of different rocks using scratch test method. The experiment was conducted on 130 quarry rocks and 236 oil and gas reservoir rocks (sandstones, limestones, dolomites and shales). The results of the tests show strong correlation between the values of intrinsic specific energy (ε) and the \({\text{UCS}}\) as shown in Fig. 5. Schei et al. [41] conducted a study on 35 sandstone and 24 carbonate samples to assess the strength and Young’s modulus (stiffness) of sedimentary rocks through scratch testing as shown in Fig. 6. The values of intrinsic specific energy (ε) obtained in their results agree with the \({\text{UCS}}\), which further validates the efficiency of scratch test for quick and effective estimation of \({\text{UCS}}\) and other geomechanical properties in rocks.

Fig. 5
figure 5

Correlation of intrinsic specific energy and uniaxial compressive strength in limestones, sandstones, and other rocks [55]

Full size image
Fig. 6
figure 6

Uniaxial compressive strength and Young’s modulus over the scratch length in carbonates and sandstones [58]

Full size image

Thin layer of weakness or heterogeneity along rock core can be captured through scratch testing, and this was showed in the rock strength estimation experiment conducted [36] using the RSD. The \({\text{UCS}}\) results from Ferreira et al. [53] uniaxial lab test and scratch test from Brazilian limestone core with high heterogeneity was presented by researchers. Their results validated the use of scratch testing to estimate \({\text{UCS}}\) and Young’s modulus in rocks such as limestone.

Fairhurst [54] combined the strength profiles with well logs to create correlations of strength and other petrophysical properties such as porosity, density, and sonic velocity. The continuous strength profile obtained provides a reliable quantitative measurement of the scale and distribution of the heterogenous properties along the tested core samples. The mechanistic basis of equivalence between a rock’s estimated intrinsic specific energy (\(\varepsilon\)) and the \({\text{UCS}}\) was further validated by using the scratch test. In their results, they observed in sedimentary rocks that in addition to the compressive strength, the Mohr–Coulomb failure envelope could also be obtained by scratch testing by the substitution of the scratching tool or cutter in order to evaluate the rock friction coefficient. The \({\text{UCS}}\) of carbonate rocks was estimated by conducting 85 uniaxial compressive tests with RSD, and the result range from 9.16 to 401.83 MPa [52]. Adachi et al. [51] attempted to investigate the rock strength under the ductile-failure mode, and the \(K_{IC}\) under the under brittle-failure mode through scratch testing method. The authors applied the Bažant’s Size Effect Law (SEL) to the experimental results to estimate \(K_{IC}\) and \({\text{UCS}}\) of different rock types. The fracture toughness values are estimated in brittle regime, while the \({\text{UCS}}\) is estimated in ductile regime.

Naeimipour et al. [55] attempted to investigate the mechanical properties of 4 different rocks (limestone, coal, conglomerate, siltstone) using scratch tests with various scratch probes. In their results, they observed high degree of agreement between the values average normal force and the compressive and tensile strengths of the rocks tested. They showed that the \({\text{UCS}}\) and Brazilian tensile strength (BTS) of the 4 different rock samples can be estimated by averaging the forces acting on the cutter in the scratch test. The authors also suggested that the rock properties can be best estimated at cutter penetration depth > 0.4 mm. The results from the study can be used for borehole probe design for evaluation of rock strength in small hole drilled for bolting or blasting.

The rock material and the strength of rock materials has been mostly mis-interpreted to be equal to intact rock and intact rock strength [56]. This misconception was clarified by Hoek and Brown [57, 58], that the intact rocks are rocks that are free from fractures and contains minimal disturbance by the core sampling process; whereas intact rock strength is the \({\text{UCS}}\) of intact rock conducted in core samples of ~ 0.061 m in diameter. The successive tests conducted [59] proposed that a rock’s principal stresses relationship at failure are characterized by two parameters, the uniaxial compressive strength and an instant rock strength parameter. The author suggested those parameters could be estimated in rocks by unconfined compression test and the Brazilian indirect tension test.

3.2 Fracture toughness (KIC)

Fracture toughness (\(K_{IC}\)) is a measure of a material’s resistance to fracture propagation. Propagating fractures tends to travel along the path of lowest resistance, but the fracture orientation, direction and limit of its path creates a complex relationship between in situ stress-field, the rock’s anisotropic mechanical properties, and the pore pressure, and fracturing pressure [34]. Williams [60] conducted scratch tests on brittle solids to investigate its scratch hardness, and the researcher observed plastic behavior aided by the high hydrostatic compressive stresses which are localized. Reliable geomechanical parameters such as \(K_{IC}\), are of upmost importance in hydraulic fracturing design and simulation to achieve successful operation and optimum hydrocarbon recovery. Notwithstanding the several attempts by researchers to investigate the elastoplastic behavior of shale rocks, its fracture characterization has not been adequately investigated. It is a common knowledge that fractures is inherently a multi-scale phenomenon, but a substantial number of studies have limited fractures to the macroscopic sphere. The novel study by Akono and Kabir [22] focused on fracture characterization in gas shales on microscopic scale using the scratch test method. The authors used shale rocks from 3 systems: Torcian Shale in Paris, Basin, France, and Lower and Upper Woodford shale in Oklahoma, USA. The authors presented a novel method of estimating fracture energy and \(K_{IC}\) in shale rocks at microscopic scale through the scratch testing method. An experiment involving four consecutive tests with an Anton Paar scratch testing machine was utilized for this study using a sphero-conical scratch probe. Akono [61] presented the macroscopic scale investigation of fracture characterization in gas shales. The test was carried out using an inclined parallel-piped blade and scratch velocities of 6 and 180 mm/min. The results validate the anisotropic fracture behavior of shale rocks at both microscopic and macroscopic scales. The author also confirmed the fractured resistance of shales is lowest when the fracture is along the bedding plane, and highest when the fracture nucleates perpendicular to the bedding plane.

Larsen et al. [62] presented a scratch force linear relationship for scratch probes with axisymmetric shapes. In the force-scaling relationship developed, the scratch probe geometries considered are conical probe, flat punch, and hemi-spherical probe. The scratch force criterion utilized for characterizing scratch resistance of materials is termed as the scratch hardness (\(H_{T}\)) [63], and it can be quantified in Eq. 7 as:

$$F_{T} \mathop = \limits^{\text{def}} H_{T} A_{c}$$
(7)

Akono et al. [64] addressed the limitation of Akono and Ulm [8] by accounting for cutter blade width in estimation of \(K_{IC}\). The force-scaling relationship for scratch probe geometries [11, 62] are well defined by Akono [61] for conical scratch probe (Eq. 8), and spherical scratch probe (Eq. 9):

$$F_{eq} = \sqrt {F_{T}^{2} + \frac{3}{5}F_{V}^{2} }$$
(8)
$$F_{eq} = \sqrt {F_{T}^{2} + \frac{665}{1188}F_{V}^{2} }$$
(9)

For crack-initiation point, Akono and Kabir [22] used threshold criterion for the energy release rate \(\left( {\mathcal{G}} \right)\), and stated that the fracture propagation occurs when \({\mathcal{G}} = {\mathcal{G}}_{f}\). Where \({\mathcal{G}}_{f}\), is the fracture energy and is the threshold value. Their scratch fracture toughness \(\left( {{\text{K}}_{s} } \right)\) estimation is given as:

$$K_{s} = \frac{{F_{T} }}{{\sqrt {2pA_{c} } }}$$
(10)

The scratch toughness of shale rock is highly dependent on scratch orientation, while the probe function, \(2pA_{c}\) is dependent on the stylus geometry and the penetration depth, \(d\). The term \(2pA_{c}\) is applicable for scratch testing using flat punch, spherical, and conical or sphero-conical scratch probe geometries. Since a sphero-conical probe was utilized, the expression for the probe function was given as:

$$2pA_{c} = \frac{4\tan \theta }{{\cos \theta d^{3} }}$$
(11)

The authors also attempted to estimate \({\mathcal{G}}_{f}\) for an anisotropic material such as shale rock, using the J-integral solution [63, 65]. The fracture energy (\({\mathcal{G}}_{f} )\) for anisotropic rocks such as shale is given as:

$${\mathcal{G}}_{f} = \frac{{1 - \upsilon^{2}_{ab} }}{{{\text{E}}_{a} }}K_{s}^{2}$$
(12)

where \(E_{a}\), is the Young’s modulus parallel to the bedding plane, while \(\upsilon_{ab}\), is the Poisson’s ratio parallel to the bedding plane.

From their results [22], the authors observed that increase in cutting depth yields higher fracture toughness \(\left( {{\text{K}}_{s} } \right)\) and focalize at an asymptotic value \(\left( {K_{s}^{\infty } } \right)\) which highlights the ductile-to-brittle transition as a function of depth of penetration. The microscopic scratch toughness estimated was observed to be to three times greater than the macroscopic fracture toughness estimated through other methods, while the microscopic fracture energy is twice as much as that estimated by other researchers at macroscopic scale. The scanning electron microscopy (SEM) result shows very rough scratch surfaces which tends to result in deflection of the fracture, due to the interaction between the shale rock’s weaker component such as clay, and much stronger constituents such as quartz. The fracture mechanical behavior observed by the authors from the SEM images are: (i) particle pull-out; (ii) fracture bridging; and (iii) fracture branching, micro-fracturing, and fracture trapping.

In a microscale experimental study by Ante et al. [66], the fracture mechanical behavior was investigated to characterize its initiation and propagation in shale and sandstone rocks using microscale mechanical scratch tests. The \(K_{IC}\) and fracture directionality were evaluated in the formation to identify the effect of grain-scale heterogeneity and inelasticity on hydraulic fracturing design and operations. Micro-scratch testing was conducted on the shale and sandstone cores used in the experiment and the cores are sourced from the Monterey formation. The continuity of core scratching increases the degree of elastic and plastic deformation of the rock. In \(F_{T}\) versus scratch length results for sandstones and shales, the instantaneous change in penetration depth along the scratch length signifies fracture occurrences. In fracture toughness estimation results presented by the authors, the values for both shale and sandstone core samples perpendicular to the bedding plane are greater the values obtained in core samples parallel to the bedding plane. Their result validates this observation made by Akono [61]. This is due to the contrasting beddings intersected during fracture toughness estimation in core samples perpendicular to the bedding plane.

In cores oriented along the bedding plane in shale rocks, \(K_{IC}\) values intersect at an average value with increase in scratch length, and this is similar to the asymptotic value (\(K_{s}^{\infty }\)) in Akono and Kabir [22]. Ante et al. [66] subsequently combined Acoustic Emission (AE) with SEM to observe the scratch area, and the damage within and outside the scratch path, to characterize the crack surface events. The authors showed (Fig. 7) the possible microscopic fracture mechanical behavior in sandstone and shale rock samples as: fracture branching, fracture bridging, particle pull-out, and fracture deflection. This validates the microscopic fracture mechanical behavior in shales already identified in [22].

Fig. 7
figure 7

Post-scratch fracture mechanical behavior a parallel to bedding plane in sandstone sample; b perpendicular to bedding plane in sandstone sample; c parallel to bedding plane in shale sample; d perpendicular to bedding plane in shale sample (after [66])

Full size image

3.3 Other parameters

Scratch testing was utilized in sanding prediction evaluation by obtaining the vertical distribution of the rock’s mechanical properties [46]. The logging measurements (GR, Sonic, porosity, and density) of the mechanical properties was obtained experimentally using the TerraTek TSI™ scratch machine. The tests conducted on 85 ft sandstone reservoir provided reliable results showing the capability of the scratch testing to (i) evaluate the vertical heterogeneity of the core; (ii) choose a number that is representative of the core sections for rock mechanical experiments; (iii) displaying the minimum vertical resolution display and log evaluation; (iv) provide quick and immediate calibration of logs for proactive decision to prevent wellbore instability and sand production.

Micro-scratch test can be resourceful in evaluating mudrock brittleness of shale rocks [67]. The results showed that the transverse force measured can be used to estimate rock brittleness index. Scratch testing also proved resourceful in studying the effect of bit wear in polycrystalline diamond compact (PDC) bits [68]. \({\text{UCS}}\) from scratch tests can be combined with sedimentology, core analysis and wireline logs to provide better characterization of rock’s heterogeneity and create continuous profile of the geomechnical properties in un-cored intervals [69].

Borehole instability issues arising from oil and gas drilling operations can addressed by predicting the strength of homogenous and heterogeneous rocks using scratch test [49]. This test was conducted on 13 carbonate and sandstone rocks with the scratching cell. Chen et al. [48] utilized the scratch testing method to evaluate continuous rock drillability by correlating the scratch test’s intrinsic specific energy and the micro-drilling tests with PDC bits. In their results, the drillability of heterogeneous sandstone from Songnan oilfield, China, was determined using combination of scratch and micro-drill tests. Filter cakes formed by various mud systems was addressed using scratch test method to determine the rock strength and stiffness and correlated them to external filter cake probing. In Cerasi et al. [70], results from the tests conducted on sandstone core samples, the scratch test technique showed the entire shear strength profile starting from the mud/cake interface to the cake/rock boundary. The authors also showed the capability of the scratch testing tool to clean-out mud filter cake layers to a lowly thickness of 0.1 mm.

4 Conclusions and recommendations

In this paper, we provided a comprehensive review of scratch test method for estimating rock strength (\({\text{UCS}}\)), fracture toughness (\(K_{IC}\)) and other geomechanical properties over the past few decades. Additionally, we presented a comparison between scratch test technique and other conventional methods. We further highlighted the methodology, modifications, and applications of the scratch test and its devices.

The advantages of scratch test method over other conventional methods in estimating rock strength and other geomechanical properties are that:

  1. (a)

    It is quasi-non-destructive, and the post-test core samples remain intact which can be utilized for other destructive or non-destructive tests.

  2. (b)

    It provides direct equivalent measurement with the rock’s \({\text{UCS}}\).

  3. (c)

    It requires limited and minimal level of sample preparation.

  4. (d)

    It is simple, quick, and highly repeatable.

  5. (e)

    It can be conducted on any dimension of rock, as the results are not affected by the core sample geometry.

  6. (f)

    It provides precise continuous profile of rock strength over the scratch interval.

As shown in Fig. 8a, the indentation test method has been more adopted in other materials such as metals, polymer/wax and ceramics/concrete than in rocks, and likewise, the scratch test is mostly used for testing rocks, followed by concrete/ceramics.

Fig. 8
figure 8

Chart showing a scratch test, indentation test, and other methods with. materials investigated; b scratch and indentation tests versus geomechanical parameters investigated

Full size image

Assessment of the chart in Fig. 8b shows that in geologic materials (rocks and unlithified sediments), scratch test is most utilized for estimating rock strength, and least for fracture toughness. This shows minimal application of scratch test method in investigating fractomechanical behavior of geological materials.

Based on the current issues, we propose the following recommendations for further research utilizing scratch test method to estimate geomechanical properties for improved hydrocarbon and geothermal exploitation and production, and geologic carbon sequestration:

  1. (a)

    Increased studies on estimation of fracture toughness in geologic materials using scratch test method.

  2. (b)

    Extended studies on fracture characterization at microscopic scales in rocks.

  3. (c)

    Further investigations on the heterogeneous microstructure and composition of rocks with a high-level accuracy.

  4. (d)

    Achieving a rock surface roughness with a lower maximum penetration depth over an extended surface area.

  5. (e)

    Application of scratch test method to characterize the fractomechanical behavior in enhanced geothermal systems (EGS).

  6. (f)

    Application of scratch test method to characterize the mechanical properties of depleted reservoirs utilized for geologic carbon sequestration.