1 Introduction

As tangible constructs (either artificial or natural), reservoirs are used as water storage for supervision, monitoring and maintenance of water supply (Hussain et al., 2011), forming the most valuable element in water resources systems. Due to environmental issues, however, construction of new dams is not an easy task; therefore, it is important that active reservoirs be boosted for the maximum effectiveness, so as to handle any present and future water-related challenges. Reservoirs are built with a dam across a flow. The major feature of a reservoir is the rule of herbal streamflow with the aid of storing surplus water within moist seasons and liberating the saved water in destiny dry seasons, thus complementing the discount in river flows. The intention is to balance streamflows and change the sequential and three-dimensional water availability. The water stored in a reservoir can be distributed later for advantageous uses, giving rise to sequential changes or reroutes through waterways or pipelines to outlying locations, and thus resulting in three-dimensional changes. Reservoir outflow projection is guided by various potential constraints, such as water storage, inflow of water, water level, evaporation, infiltration, geomorphology, and other factors, all of which need to be considered, so as to understand the ambiguity. Plentiful methods have been used in forecasting hydrological practices over the past years. Traditional tactics used are of linear mathematical relationships based on the capability of machinists, a simple set of curve fitment, and standards employed to quote reservoir water outflows (Tokar & Markus, 2000). However, poor performances are found in numerical models, due to their unavailability and complexity of statistics, missing datapoints and overemphasized constraints. Various machine learning algorithms have been used in previous research, with an intention to overcome these concerns and estimate reservoir water outflows (Mokhtar et al., 2014; Seckin et al., 2013). Subsequently, many Machine Learning (ML) models, including Artificial Neural Networks (ANNs), Radial Basis Neural Networks (RBNN), Support Vector Machines (SVMs), Adaptive Neuro-Fuzzy Inference Systems (ANFIS), Logistic Regression (LR), etc., have been deployed in water management systems progressively, so as to improve the consistency and precision of the estimation models (Ahmadlou et al., 2019; Bowden et al., 2002; Naghibi & Pourghasemi, 2015). Modelling a machine to work and improvise on its own without explicit programming each time is called ML. In intellectual studies, ML shows the capability to solve complex problems at a high level of accuracy and can make predictions as demanded for certain future periods (Mullainathan & Spiess, 2017). Nowadays, AI models have been extended successfully to the field of reservoir operation. Compared to conventional physical prediction models, ML models can, with the help of historical dataset, learn numerous hydrological operations independently at acceptable correct operating rates. Advantages of such modelling lie in the capability of their software system to map input–output models (Hejazi & Cai, 2009; Hipni et al., 2013; Najah et al., 2011). To forecast daily water levels, five different ANN models were tested each with an increasing number of inputs, finding that the accuracy began to decrease with the addition of many inputs. The reason for this is that the network started to be obsolete and irrelevant, as explained in the research (Nwobi-Okoye & Igboanugo, 2013). By comparing the performance of SVM and multilayer perceptron (MLP), it is found that due to the optimization algorithms, SVM has a great deal of capacity to resolve a linearly constrained quadratic programming function, and the optimum kernel function in this case is a radial basis kernel function (Khan & Coulibaly, 2006). During the process of creating fuzzy membership functions, a study on the ANFIS technique observed that triangular and trapezoid membership functions were deemed to be more suitable than bell-shaped membership functions (Shafaei & Kisi, 2016). In addition, a genetic algorithm (GA) was successfully utilized in optimizing reservoir operations; and by using data collected in a longer period of time, the GA model could be further improved for reservoir water levels (Onur Hınçal et al., 2011). Many more AI methods, such as the adaptive network-based fuzzy inference system (ANFIS), genetic algorithm (GA) and decision tree, have been effectively applied in the reservoir operation field, in addition to these AI algorithms . In fact, many reservoirs in California have used the improved decision tree (DT) algorithms, classification methods and regression trees to estimate water storage or release (Yang et al., 2016).

In this study, five models of the SVM algorithm and Regression tree (RT) algorithm were compared with an increasing number of inputs by using 5-, 10- and 20-fold cross-validation for original data, so as to accurately forecast fluctuations of the water level of Rupnagar's Bhakra reservoir (Ropar). A lot of quantitative metrics, including root mean square error (RMSE), correlation coefficient (R2), and mean absolute error (MAE), were used to validate and compare these models; and MATLAB R2021b was used to design and code the modelling and data procedures.

2 Materials and methods

2.1 The study area

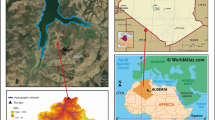
Bhakra Dam on the Sutlej River (Bilaspur, Himachal Pradesh) is a concrete gravity dam in the northern part of India, with geographic coordinates of 31°24′39″N latitude and 76°26′0″ E longitude. The dam is considered to be the highest gravity dam in the world. The Sutlej River, a major tributary of the Indus River, originates in Tibet and flows into the Indo-Gangetic plains near Bhakra. The overall upriver catchment area of the Bhakra River is 56,980 km2. The precipitation in the catchment changes around an annual average of about 875 mm. Situated in a canyon near the (now submerged) upstream Bhakra community in the Himachal Pradesh district of Bilaspur, the dam is 226 m high, 518.25 m long and 9.1 m wide. Its “Gobind Sagar” reservoir can hold up to 9.34 billion cubic metres of water. The Bhakra dam generates a 90-km-long reservoir, covering 168.35 square kilometres and forming India's third-largest reservoir in terms of water storage capacity. The Bhakra Beas Management Board (BBMB) is in charge of the dam's operation and maintenance.

As a straight gravity cum concrete dam, Bhakra Dam has four radial spillway gates and an 8212 cumec designed overflow capacity. The location of the study area is shown on the map in Fig. 1. The Nangal reservoir is built with a 28–95 m high dam, situated at about 11 km downstream of the Bhakra dam. It controls irrigation releases by acting as a head regulator. During the monsoon, the dam would retain extra water; and then, it would release the water gradually throughout a year. It also prevents flood damage caused by monsoon rains. This dam feeds the Bhakra canal, which irrigates 10 million acres (40,000 km2) of land in Haryana Punjab and Rajasthan. Table 1 shows the characteristics of the Bhakra Nagal dam and reservoir.

Fig. 1
figure 1

Bhakra Dam’s location

Full size image
Table 1 Characteristics of Bhakra Nagal Dam and Reservoir
Full size table

2.2 Data collection

A total of 2976 historical data points (for 30 years) were used, including: the reservoir level (M), the monthly reservoir storage (BCM), the previous inflow of reservoir (MCM), the current inflow of reservoir (MCM), the evaporation of reservoir (MCM), the previous outflow of the reservoir (MCM), and time (months) and release of the reservoir. All the data were acquired from the following websites: “UK Centre for Ecology and Hydrology”, “Bhakra Beas Management Board” and “India Meteorological Department”. The range of the reservoir’s water level is determined by the hydraulic features of the Bhakra dam, with the maximum water level at 512.06 m and the minimum operating level at 450.45 m. Table 2 shows the essential statistical properties of the inputs, such as the minimum, maximum and total count values.

Table 2 Data acquired with descriptive statistics
Full size table

One of the tasks during modelling nonlinear hydrological processes was to select the most significant variables from the whole set of input variables (Bahrami & Wigand, 2018; Hu & Wan, 2009). The major goal of data collection in this study is to choose appropriate input variables, depending on the data available. Also known as feature selection, the choice of the best subset of the inputs in the model was made based on certain defined governing rules (Sharafati et al., 2019), so as to increase the model’s accuracy and efficiency. Therefore, during the modelling phase of this study, various combinations of input variables were used. For this study, five scenarios are initially defined at different folds, as shown in Table 3, so as to find out the most effective output. Then, the prediction accuracy was evaluated for each scenario.

Table 3 The selected scenarios for input combinations
Full size table

2.3 Support vector machine (SVM)

Support Vector Machine has gained popularity as a novel statistical learning method over recent two decades. Used for both classification and regression, it proves an efficient and reliable approach (Collobert & Bengio, 2001; Drucker et al., 1996; Vapnik, 1995). Unlike the traditional chaotic methods, the SVM method is based on the idea of mapping input data into a high-dimensional feature space, so as to help with classification and simulate unknown relationships between the set of input variables and the set of output variables. Based on the mechanism’s simplicity, two advantages of this method are that it is sufficiently known by scientists and that it dominates prediction. It has a level of precision that sets it apart from several other approaches. SVM is a strategy that uses a kernel trick to understand an issue, while simultaneously lowering the complexity and prediction errors of models. SVM classification is the first step in making a decision limitation for the feature space, which is delivered by generating an ideal separation hyperplane between two classes, so as to maximize the margin by minimizing the generalization error. In theory, SVM classification has the potential to predict outcomes, which can be comprehended with three essential concepts: (1) Function of the kernel; (2) The soft-margin; and (3) The separation hyperplane (Cristianini & Shawe-Taylor, 2000; Schwefel, 1981). Polynomial, radial basis and sigmoid, functions are exemplary kernel functions. Algorithms like SVM are mostly used to forecast classification problems and support vector regression (SVR) is an expansion of SVM by adding an insensitive loss function, so that it can be used in regression analysis (Drucker et al., 1996; Kim et al., 2012). In other words, in a classification problem, SVM is utilised to partition data into “+1” and “− 1” classes. On the other hand, SVR is a generalized SVM approach to predict random real values (Basak et al., 2007; Gunn, 1988). To improve forecasting of reservoir inflows, a modified SVM-based prediction system was created (Li et al., 2010). Climatic data from previous time periods were used, in addition to highly connected climate precursors. To understand non-linear patterns underlying climatic systems more flexibly, SVM parameters were determined in a genetic algorithm-based parameter determination approach. The median of forecasts from the created models was then used to reduce the variation in the prediction by using bagging to construct several SVM models. In terms of the predictive ability, the suggested modified SVM-based model outperformed a bagged multiple linear regression (MLR), a simple SVM, and a simple MLR model.

Regression with an alternate loss function is an example of SVM. Loss functions are frequently used in estimation, model selection, and prediction; and they are critical in determining any disparities between the null and nonparametric models’ fitted values (Hong & Lee, 2009). In terms of hydrology, researchers must consider loss functions when making predictions. In this study, a hydrologic loss function is used to link two primary variables: rainfall and runoff. A distance measure must be supplied, which necessitates a change in the loss function (Smola & Scholkopf, 2004). SVR’s main notion is to nonlinearly translate the initial data into a higher-dimensional feature space, so as to solve the linear regression issue (Fig. 2). As a result, SVR is usually required to construct a suitable function f(x) to reflect the non-linear relationship between feature xi and target value yi, as demonstrated in Eq. (4).

$$f\left({x}_{i}\right)=w \varphi ({x}_{i})+ {b \| w\| }^{2}$$
(1)

where w denotes the coefficient vector, \(\varphi\) (\({x}_{i}\)) denotes the transformation function, and w and b denote the weight and bias, respectively, which are calculated by minimising the so-called regularised risk function, as shown in Eq. (5).

$$\mathrm{R}(\mathrm{w}) = \frac{1}{2}{\| w\| }^{2}+c\sum_{i=1}^{n}{L}_{\varepsilon }({y}_{i},\mathrm{f}({x}_{i} ))$$
(2)

where \(\frac{1}{2}{\| w\| }^{2}\) is the regularization term; \(c\) is the penalty coefficient; and \(L\varepsilon ({y}_{i},\mathrm{f}({x}_{i} ))\) is the \(\varepsilon\)-insensitive loss function, which is calculated according to Eq. (6).

$$L\varepsilon \left({y}_{i},\mathrm{f}\left({x}_{i} \right)\right)=\mathrm{ max}\{0,\left|{y}_{i}-\mathrm{f}\left({x}_{i} \right)\right|-\varepsilon \}$$
(3)

where ε signifies the allowed error threshold, which will be ignored if the projected value is within the scope of the threshold; otherwise, the loss will equal to a number greater than ε.

Fig. 2
figure 2

Schematic diagram of SVR (Zhang et al., 2018)

Full size image

To find out the optimization boundary, two slack factors, \({\xi }^{+}\) and \({\xi }^{-}\), are introduced:

$$\mathrm{min}f\left(\mathrm{w}, {\xi }^{+},{\xi }^{-}\right)=\frac{1}{2}{\| w\| }^{2}+c\sum_{i=1}^{n}( {\xi }^{+},{\xi }^{-})$$
(4)

Subject to

$${y}_{i}-\left[\mathrm{w}. \varphi \left({x}_{i} \right)\right]-\mathrm{b }\le\upvarepsilon +{\xi }^{-},{\xi }^{-} \ge 0$$
$$\left[\mathrm{w}. \varphi \left({x}_{i} \right)\right]+\mathrm{b}-{y}_{i}\le\upvarepsilon +{\xi }^{+},{\xi }^{+} \ge 0$$
(5)

The minimization of a Lagrange function, which is formed from the objective function and the problem constraints, yields the dual version of this optimization problem:

$${\mathrm{max\alpha },\mathrm{ \alpha }}^{*}= \frac{1}{2}\sum_{i,j=1}^{N} ({\mathrm{\alpha }}_{i }-{{\mathrm{\alpha }}^{*}}_{i}),({\mathrm{\alpha }}_{j }-{{\mathrm{\alpha }}^{*}}_{j} )\mathrm{K}{(x}_{i},{x}_{j})-\upvarepsilon \sum_{i=1}^{N}\left( {\mathrm{\alpha }}_{i}+{{\mathrm{\alpha }}^{*}}_{i}\right) +\upvarepsilon \sum_{i=1}^{N}{y}_{i}\left( {\mathrm{\alpha }}_{i}-{{\mathrm{\alpha }}^{*}}_{i}\right),$$
(6)
$$\begin{aligned}\text{s}.{\text{t}} \quad & \sum_{i=1}^{l} ({{\alpha }}_{i }-{{{\alpha }}^{*}}_{i})=0, \quad \text{i}=1 \; \text{to} \;N, \\ & {{\alpha }}_{i }, {{{\alpha }}^{*}}_{i} \ge 0 \quad { i}=1 \; \text{to} \;N, \\ & -{{\alpha }}_{i },{-{{\alpha }}^{*}}_{i}- \ge -{C} \quad {i}=1\text{to}\; N. \end {aligned}$$
(7)

The inner product\(\{\varphi \left({x}_{i} \right),\varphi \left({x}_{j}\right)\)} in the feature space is denoted by the function K(x i, x j) in the dual formulation of the issue.

Any function \(K{(x}_{i},{x}_{j})\) can become a kernel function, if it satisfies the inner product criteria. Hence, the regression function can be expressed as follows:

$$f(\mathrm{x})=\sum_{i=1}^{N} ({\mathrm{\alpha }}_{i }-{{\mathrm{\alpha }}^{*}}_{i})\mathrm{K}{(x}_{i},{x}_{j})+\mathrm{b}$$
(8)

2.4 Regression tree (RT)

As a machine-learning algorithm for building prediction models from datasets, Regression Tree employs a clustering tree with post-pruning processing. The clustering tree algorithm is often referred to as the forecasting clustering tree and the monothetic clustering tree (Chavent, 1988; Vens et al., 2010). Regression Tree is used for model-dependent variables having a finite number of values which are not arranged in order, with prediction errors commonly assessed as the squared difference between the predicted and observed values (Loh, 2011). Clustering tree algorithms are based on the top-down induction technique of decision trees (Quinlan, 1986). Regression Tree algorithms take a collection of data for training and create a new internal node as good as possible. Based on the decreased variance, such algorithms choose the top test scores. The lower the variance, the more homogeneous the cluster and the more accurate the forecast. If none of the tests significantly reduce variance, a leaf will be generated and marked as data representative (Chavent, 1988; Vens et al., 2010). By recursively splitting the data space and fitting a prediction model within each partition, a hierarchical tree-like division of the input space can be created (Breiman, 2017). A sequence of recursive splits divides the input space into local regions, which are designated by a series of recursive splits. Internal decision nodes and terminal leaves make up the tree finally. Starting at the root node, a sequence of tests and decision nodes will determine the path through the tree, till it approaches a terminal node, providing a test data point. A prediction is made at the terminal node based on the model linked to that node locally.

2.5 K-fold cross-validation

The holdout approach can be employed when the amount of data available for training and testing are limited. In this approach, a subset of data is saved for validation, while the rest is for training. It is a common practice in engineering to keep one-third data for validation and utilize the other two-thirds for training and testing (Witten & Frank, 2000). By dividing the obtained data into a specified number of equally sized observations or folds (k), the holdout approach can be further improved. The dataset used for testing is chosen from these (k) folds, whereas the rest (k-1) is employed in the training process. This procedure will be repeated for k times, with a different fold being tested in each time and the remaining folds (k-1) serving as the training dataset. As a result, the approach would generate k different degrees of accuracy. The variance of the resulting estimate diminishes as (k) will be increased. Consider a fivefold cross-validation scenario (k = 5). Figure 3 shows how the dataset is divided into five folds. The first fold is used to test the model, while the others are used to train the model in the first iteration. Then, the second iteration uses the second fold as the testing set and the rest as the training set. This procedure will be repeated until each of the five folds has served as a testing set.

Fig. 3
figure 3

Cross-validation in different folds

Full size image

3 Results and discussions

The best value of each grouping would result in the most precise estimating model; and later, the unsurpassed grouping combination would be chosen. The data were divided into two categories: Regression tree and SVM analysis. Following this process, two models were employed to make data projections based on five diverse scenarios. The most appropriate and exact prediction scenario was determined by each model’s best estimation. To decide whether a model was best, the estimating power of both models was examined. To evaluate the suggested model’s execution in varied in preparing, checking and testing information, three types of measurable assessments were used, i.e., RMSE, MAE and \({R}^{2}\). Figures 4 and 5 show the comparison of the observed values with the predicted values of outflows by using SVM and RT models for 5-, 10- and 20-fold cross-validation. It can be clearly seen from the figures that the predicted values are much closer to the observed ones for Scenario 5 with tenfold cross-validation using SVM model. Figures 6 and 7 depict the residuals obtained by using SVM and RT models for different cross-validation conditions. Residuals obtained are the minimum for SVM models as compared to RT models and are best for tenfold cross-validation condition. Table 4 contrasts the calculations statistically for the model SVM computed by using fivefold cross-validation. Data observed from the table clearly show that Scenario 5 relates to the lowest RMSE, MAE values and a maximum \({R}^{2}\) value amid all the situations. Moreover, data forecasting in Scenario 5 offers the most accurate results, while Scenario 4 provides the second lowest result. Besides, Scenario 3 has erratic forecasts, compared to all other scenarios. The lowest value for authentication oversights RMSE is also held by Scenario 5. Continuous development can be seen in the results from Scenarios 1–2 in SVM Regression. A big inaccuracy from Scenarios 2 to 3 of the SVM was recorded in the values of RMSE; MAE would increase, while the coefficient of correlation decreased from 0.87 to 0.85.

Fig. 4
figure 4

Relationship between the observed outflow and the predicted outflow by using SVM, fivefold (a), tenfold (b) and 20-fold (c)

Full size image
Fig. 5
figure 5

Relationship between the observed outflow and the predicted outflow by using RT, fivefold (a), tenfold (b) and 20-fold (c)

Full size image
Fig. 6
figure 6

Residue plots for the SVM model at the monthly scale, fivefold (a), tenfold (b) and 20-fold (c)

Full size image
Fig. 7
figure 7

Residue plots for the RT model at monthly scale, fivefold (a), tenfold (b) and 20-fold (c)

Full size image
Table 4 Statistical evaluation of support vector machine for fivefold cross-validation
Full size table

Table 5 compares and contrasts the statistical evaluations for the SVM model using tenfold cross-validation. It can be observed that Scenario 5 for SVM using tenfold cross-validation does necessarily produce better results than fivefold cross-validation. The RMSE and MAE values obtained with tenfold cross-validation seem to be more accurate than those obtained with fivefold cross-validation, as shown in Table 4. On the other hand, R2 has the same value as fivefold cross-validation. Except for the R square value, i.e., 0.9, tenfold cross-validation yields better results than fivefold cross-validation for all parameters, which is the same as fivefold cross-validation. In the same way, Table 6 shows a comparison of the statistical assessments for the SVM model using 20-fold cross-validation, purposed to determine whether a greater cross-validation number may minimise the predicting errors. It shows that SVM model Scenario 5, which uses 20-fold cross-validation, may not always deliver better results than fivefold and tenfold cross-validation. Scenario fivefold and tenfold cross-validation yields lower RMSE values than 20-fold cross-validation. Fivefold and tenfold cross-validation has R square values closer to 1 as compared to 20-fold cross-validation. Table 7 displays the results of fivefold cross-validation using regression tree models under various assessment criteria. It can be observed that all of the scenarios have extremely strong prediction ability (R2 > 0.77), according to the statistical assessment standards of this study. Scenario 3 achieves the best result, since it has the highest \({\mathrm{R}}^{2}\) value (0.82), followed by Scenarios 2, 4, 1 and 5. In terms of RMSE, Scenario 5 gives the best predictive power (602.8), followed by Scenarios 3, 4, 2 and 1. Table 8 shows that Scenario 4 of Regression tree model using tenfold cross-validation has very good predictive ability, since it gives the best R2 value (0.85), the lowest RMSE (557.48) and the lowest MAE (270.23), followed by Scenario 2. As clearly seen in Table 9, the results of the Regression tree of Scenario 1 using 20-fold cross-validation are overall better than those for both fivefold and tenfold cross-validation. The computed RMSE values are higher than tenfold cross-validation. Table 10 compares the predicted outcomes based on two distinct AI models, i.e., Regression Tree and Support Vector Machine, united with various parameters of the model. The findings reveal that the SVM model with tenfold cross-validation [RMSE (452.17), R2 (0.9)] performs the best when compared to other SVM and RT models.

Table 5 Statistical evaluation of support vector machine for tenfold cross-validation
Full size table
Table 6 Statistical calculation of Support Vector Machine for 20-fold cross-validation
Full size table
Table 7 Statistical calculation of Regression tree for fivefold cross-validation
Full size table
Table 8 Statistical calculation of regression tree for tenfold cross-validation
Full size table
Table 9 Statistical calculation of regression tree for 20-fold cross-validation
Full size table
Table 10 Statistical calculation of regression tree model and support vector machine model
Full size table

4 Conclusion

Over the past decades, traditional hydrological forecasting models have greatly changed, with SVM taking the prominence, because it can offer accurate data forecasts for a variety of hydrological processes. The ability to accurately estimate changes in reservoir water levels is beneficial for the planning and management of reservoir water usage in the long run. By examining two distinct Machine Learning approaches, i.e., Regression Tree and Support Vector Machine, this study tries to find which one is the most accurate in predicting water levels based on monthly hydrological records collected in the past 30 years, so as to simulate reservoir outflows. To get the best parameters, this study evaluated a variety of scenarios based on a variety of data inputs. For this purpose, RMSE, MAE and \({\mathrm{R}}^{2}\) indices are used to quantify the performance of the forecasting models. In summary, Scenario 5 shows the optimum combination of input data, which comprise inflow, evaporation, water level, reservoir storage, previous inflow and previous outflow. The best SVM regression is with quadratic kernel function, and the best V-fold cross-validation is tenfold, which is employed for the optimal scenario selection. In the comparative analysis of water level prediction by the two algorithms, SVM is proven to be the best algorithms for water level prediction. However, when performing water level prediction individually, Regression tree with tenfold cross-validation shows that the SVM model can make accurate predictions. This highlights its unique capabilities and benefits in detecting hydrological time series with nonlinear properties. Therefore, SVM has certain generality and can be used as a model for reservoir water level prediction. More kind of hydrological data, such as infiltration rates, transpiration rates, low inflow conditions and other relevant parameters, should be added in future studies, so as to deliver more precise forecasts.