1 Introduction

The investigation of soliton solutions for nonlinear evolution equations (NLEEs) has emerged as an emerging area of research with far-reaching implications across various scientific disciplines, including plasma physics, fluid dynamics, ocean engineering, optical fiber communication, and mechanical engineering, among others. The origins of soliton theory can be traced back to the observations made by Scottish scientist John Scott Russell [1] in 1834. However, it was the work of Zabusky and Kruskal [2] in 1965 that demonstrated the significance of soliton wave solutions. In their study, they established the celebrated Korteweg-de-Vries (KdV) equation and revealed that by balancing the highest-order linear and nonlinear terms, a soliton solution could be obtained. Several researchers disclosed that soliton wave solutions can propagate a long distance with unchanged shape and velocity, even when colliding with other solitons. In ocean engineering, soliton wave theory is crucial for controlling destructive waves occurred in ocean. In communication system, it is used to transmit data over long distance without any significant distortion and attenuation. Several researchers investigated soliton and wave solutions applicable in ocean engineering, marine and coastal engineering, communication systems, and other scientific fields. For example, Shakeel et al. [3, 4], Zhang et al. [5], Shakeel et al. [6, 7], Shah et al. [8], Ismail et al. [9,10,11], and Shakir et al. [12] conducted several significant studies on soliton theory. As all natural incidents are inherently nonlinear, the NLEEs are being utilized to model the physical events come about in real-life problems. Due to their nonlinear nature, NLEEs possess soliton solutions that play a remarkable role in disclosing the nature of the problems and ascertaining a wide range of ways to make advancement in the relevant fields. Several academics have made significant efforts to formulate a universal scheme to examine all NLEEs. Consequently, numerous approaches have been developed, though none of them are ubiquitously applicable. For instance, the modified extended direct algebraic method [13, 14], the generalized tanh-coth method [15], the Mohand transformation method [16], the extended \(F\)-expansion method [17], the generalized Kudryashov method [18, 19], improved F-expansion method [20, 21], the modified differential transform method [22, 23], the optimal perturbation method [24], the extended rational sinh-cosh method [25], the modified fractional homotopy analysis transform method [26], the fractional sub-equation method [27],the mapping method [28], the \(({G}{\prime}/G)\)-expansion method [29, 30], the extended \(({G}{\prime}/G)\)-expansion method [31], the \(({G}{\prime}/G\),\(1/G)\)-expansion method [32, 33], etc.

Nowadays, the fractional differential models are being used universally due to its ability to explore any phenomena more precisely than the integer ordered differential models. In contemporary times, fractional differential models have gained widespread use due to their further precision in searching various phenomena compared to integer-ordered differential models. The fractional derivative (FD), a branch of differential calculus focuses on the fractional order derivative rather than integer order. The origin of FD can be traced back to the correspondence between Leibniz and L’ Hospital in 1695, and it has since flourished through the efforts of several researchers who have strived to formulate robust definitions of FD. As a result, several reliable definitions have emerged, including the Grunwald–Letnikov FD [34], the Riemann–Liouville fractional derivative [35], the Caputo FD definition [36], the beta FD definition [37], and the conformable FD definition [38], etc. The beta fractional derivative, introduced by Atangana et al. [39], is the most recent definition and has not exhibited any known drawbacks so far. The beta derivative is defined as follows:

The beta fractional derivative: For any function \(w\left(t\right)\), the beta derivative of the function is.

\({D}_{x}^{\beta }w\left(t\right)=\underset{h\to 0}{\mathrm{lim}}\frac{w\left(t+h{\left(t+\frac{1}{\Gamma \beta }\right)}^{1-\beta }\right)-w(t)}{h},\)

Together with \(h={\left(t+\frac{1}{\Gamma \beta }\right)}^{\beta -1}k\), \(0<\beta \le 1\), \(k\) is an arbitrary constant.

The model equation: In 2006, Wazwaz [40] discussed the modified \(\alpha\)-equation in his study on fluid dynamics. This equation is used in fluid dynamics to describe turbulence, and can be stated as:

$${w}_{t}-{w}_{xxt}+(\alpha +1){w}^{2}{w}_{xx}-b{w}_{x}{w}_{xx}-{w}_{xxx}=0.$$
(1.1)

Equation (1.1) alters to the modified Camassa-Holm (CH) equation for \(\alpha =2\), and holds the form:

$${w}_{t}-{w}_{xxt}+3{w}^{2}{w}_{xx}-b{w}_{x}{w}_{xx}-{w}_{xxx}=0$$
(1.2)

Subsequently, another form is derived from of this equation named the simplified modified Camassa-Holm equation which takes the form [41]:

$${w}_{t}+2a{w}_{x}-{w}_{xxt}+b{w}^{2}{w}_{x}=0$$
(1.3)

The simplified mCH equation is a simplification version of the CH equation, which models the dynamics of shallow water waves. This equation neglects some of the dispersion and nonlinear effects that are present in the original CH equation, but it still captures some important features of wave dynamics. Now, if we consider the beta fractional derivative for the differentiation with respect to time \(t\), the simplified mCH equation can be written as

$${D}_{t}^{\beta }w+2a{w}_{x}-{D}_{t}^{\beta }\left({w}_{xx}\right)+b{w}^{2}{w}_{x}=\mathrm{0,0}<\beta \le 1,$$
(1.4)

where the first term is the time evolution of the wave function \(w=w(x,t)\),\({w}_{x}\) describes the advection of wave due to the mean flow of wave in \(x\)-direction, third term defines the dispersive effects of the fluid, which cause the wave to spread out over time, and the last term labels the nonlinearity of fluid. In the meantime, the parameters \(a\) and \(b\) represents the strength of advection and nonlinearity of the wave, respectively.

Several approaches have been exploited to search out the exact traveling wave solutions to the aforementioned Eqs. (1.3) and (1.4). Islam et al., [42] adopted the extended Riccati method that delivered singular kink-shaped, singular periodic, compacton, singular anti-bell-shaped, kink-shaped, and singular compacton solitons; Zafar et al., [41] adopted the extended Jacobi’s elliptic function expansion, the new Kudryashov and the \({\mathrm{Exp}}_{a}\)-function approaches and derived bell-shaped, anti-bell-shaped, and rogue wave solutions; Shakeel et al., [43] employed the novel \(\left({G}{\prime}/G\right)\)-expansion method, which yielded kink, periodic, and singular kink solitons; Fang et al., [44] utilized the homotopy perturbation method that provided with anti-bell-shaped, singular kink, and flat kink solitons; and many others considered several schemes to investigate soliton solution of the concerned equations.

The \(({G}{\prime}/G,1/G)\)-expansion method is a concise and purist technique that has not been exploited to establish solitary wave solutions to the simplified mCH equation in the former research. Therefore, this research aims to obtain the soliton solution of the beta fractional simplified mCH equation using the \(({G}{\prime}/G,1/G)\)-expansion method for theoretical calculations. As a result, the article presents several new solutions for the aforementioned equation.

The remaining sections of this article are structured as follows: Sect. 2 provides a detailed explanation of the technique; the method is employed to extract the analytical solutions of the time-fractional simplified mCH equation in Sect. 3. Section 4 presents a comparison of the results obtained. In Sect. 5 , we have illustrated the graphical features of solutions. At last, Sect. 6 is entitled to the conclusion.

2 Outlines of method

The key steps which are to be followed to put in use the \(\left({G}{\prime}/G, 1/G\right)\)-expansion approach have been summarized in the subsequent context. Suppose a FNLEE, which has to be investigated, is given in the following form:

$$W\left(w,{w}_{{x}_{1}},{w}_{t},{w}_{{x}_{2}},{w}_{t{x}_{1}},\dots ,{D}_{t}^{\beta }w,{D}_{{x}_{1}}^{\beta }w,\dots \right)=0, 0<\beta <1.$$
(2.1)

The given FNLEE contains a polynomial \(w\) of the wave function \(w=w(t, {x}_{1},{x}_{2},\dots )\) and its various fractional derivatives. To implement the mentioned method, the given FNLEE has to be converted to a nonlinear differential equation through wave transformation. As we consider beta derivative for fractional differentiation, the wave transformation is.

$$w\left({t,x}_{1},{x}_{2},\dots \right)=r\left(\Theta \right),$$
(2.2)

together with \(\Theta =\pm {\frac{{\varrho }_{1}}{\beta }\left({x}_{1}+\frac{1}{\Gamma \beta }\right)}^{\beta }\pm \frac{{\varrho }_{2}}{\beta }{\left({x}_{2}+\frac{1}{\Gamma \beta }\right)}^{\beta }\pm \dots \pm \frac{\Omega }{\beta }{\left(t+\frac{1}{\Gamma \beta }\right)}^{\beta }\), which is the new wave variable, \(r(\Theta )\) stands for the wave amplitude with velocity \(\Omega\), while \({\varrho }_{1}\), \({\varrho }_{2}\),… be the wave numbers in the corresponding directions \({x}_{1}\), \({x}_{2}\),…, and \(\beta\) defines the fractional order of differentiation. The implication of the wave transformation to Eq. (2.1) converts the equation to a nonlinear differential equation in \(r(\Theta )\).

$$R\left(r,{r}^{\prime},{r}^{{\prime}{\prime}},{r}^{{\prime}{\prime}{\prime}},\dots \right)=0.$$
(2.3)

Here, the prime is used to denotes the conventional differentiation of \(r(\Theta )\) with respect to \(\Theta\).

The following strategies should be executed to resolve NLEEs using the \((G{\prime}/G\),\(1/G)\)-expansion approach.

Step-1: As per the presented method, Eq. (2.3) admits an exact traveling wave solution that can be expressed as a series of combination of two functions as follows:

$$r\left(\Theta \right)=\sum_{k=0}^{N}{{\tau }_{k}({G}{\prime}/G)}^{k}+\sum_{k=1}^{N}{\sigma }_{k}{({G}{\prime}/G)}^{k-1}(1/G),$$
(2.4)

with \(k\) being a positive integer determined through the principle of balance. The constants \({\tau }_{k}\), \({\sigma }_{k}\) are arbitrary, while \(G=G(\Theta )\) satisfies the second-ordered equation:

$${G}^{{\prime}{\prime}}\left(\Theta \right)+\lambda G\left(\Theta \right)=\mu ,$$
(2.5)

where \(\lambda\), \(\mu\) are free parameters. Afterward, the succeeding relations can be assessed

$${\upchi }{\prime}=-{\upchi }^{2}+\mu\Pi -\lambda , {\Pi }{\prime}=-\mathrm{\chi \Pi },$$
(2.6)

with \(\upchi \left(\Theta \right)={G}{\prime}/G,\Pi \left(\Theta \right)=1/G\).

The general solution of Eq. (2.5) can be categorized into three cases, which are discussed below.

Case 1: When \(\lambda >0\), the general solution involves combination of trigonometric functions as follows:

$$G\left(\Theta \right)={\Upsilon }_{1}\mathrm{sin}\left(\sqrt{\lambda }\Theta \right)+{\Upsilon }_{2}\mathrm{cos}\left(\sqrt{\lambda }\Theta \right)+\frac{\upmu }{\lambda },$$
(2.7)

along with \({\Pi }^{2}=\frac{\lambda \left({\upchi }^{2}-2\mathrm{\Pi \mu }+\lambda \right)}{{\lambda }^{2}\Lambda -{\upmu }^{2}}\), \(\Lambda ={\Upsilon }_{1}^{2}+{\Upsilon }_{2}^{2}\), and \({\Upsilon }_{1}\), \({\Upsilon }_{2}\) are arbitrary parameters.

Case 2: When \(\lambda <0\), the general solution of Eq. (2.5) is constructed with the aid of the hyperbolic functions and takes the form:

$$G\left(\Theta \right)={\Upsilon }_{1}\mathrm{sinh}\left(\sqrt{-\lambda }\Theta \right)+{\Upsilon }_{2}\mathrm{cosh}\left(\sqrt{-\lambda }\Theta \right)+\frac{\upmu }{\lambda },$$
(2.8)

together with \({\Pi }^{2}=-\frac{\lambda \left({\upchi }^{2}-2\mathrm{\Pi \mu }+\lambda \right)}{{\lambda }^{2}\Lambda +{\upmu }^{2}}\), \(\Lambda ={\Upsilon }_{1}^{2}-{\Upsilon }_{2}^{2}\), and \({\Upsilon }_{1}\), \({\Upsilon }_{2}\) are arbitrary parameters.

Case 3: When \(\lambda =0\), the general solution of Eq. (2.5) involves rational algebraic functions and holds the form as:

$$G\left(\Theta \right)=\frac{\mu }{2}{\Theta }^{2}+{\Upsilon }_{1}\Theta +{\Upsilon }_{2},$$
(2.9)

along with \({\Pi }^{2}=\frac{1}{{\Upsilon }_{1}^{2}-2{\mathrm{\mu \Upsilon}}_{2}}\left({\upchi }^{2}-2\mathrm{\mu \Pi }\right)\), \({\Upsilon }_{1},{\Upsilon }_{2}=\) arbitrary parameters.

Step-2: Plugging in the values of \(r\left(\Theta \right)\) and its derivatives into (2.3), an equation can be derived that includes \({\upchi }^{\mathrm{k}}\left(\Theta \right)\), \({\Pi }^{\mathrm{k}}(\Theta )\), and their respective derivatives. Replacing the derivatives and \({\Pi }^{2}(\Theta )\) by their values, the derivatives and higher order of \(\Pi \left(\Theta \right)\) are to be eliminated from the obtained equation.

Step-3: An algebraic system of equations is accomplished by equating the coefficients of \({\upchi }^{k}{\Pi }^{k}(k=\mathrm{0,1},\dots N;k=\mathrm{0,1})\) on both sides of the obtained equation. Solving these equations leads to a range of solutions to the differential Eq. (2.3). Once these solutions are extracted, we can attain our desired exact traveling wave solutions of FNLEE (2.1) utilizing the wave transformation Eq. (2.2).

3 Solutions to the simplified modified time-fractional CH equation

Through the wave transformation, Eq. (1.4) will be altered to the subsequent nonlinear equation.

$$2a\varrho {r}^{\prime}\left(\Theta \right)-\Omega {r}^{\prime}\left(\Theta \right)+b\varrho {r\left(\Theta \right)}^{2}{r}^{\prime}\left(\Theta \right)+{\varrho }^{2}\Omega {r}^{\left(3\right)}\left(\Theta \right)=0,$$
(4.1)

with \(\Theta =\varrho x-\frac{\Omega {(t+\frac{1}{\Gamma \beta })}^{\beta }}{\beta }\), \(\varrho =\) wave number, and \(\Omega =\) velocity of wave.

Integrating both sides of (4.1) and considering the integration constant zero, the resultant equation is.

$$6a\varrho r(\Theta )-3\Omega r(\Theta )+b\varrho {r\left(\Theta \right)}^{3}+3{\varrho }^{2}\mathrm{\Omega r}^{\prime\prime} (\Theta )=0.$$
(4.2)

The value of the balance variable \(k\) is estimated by balancing the order between \(r{\prime}{\prime}\) and \({r}^{3}\), \(i.e.\), \(3k=k+2\). Thus, the derived value is \(k=1\). As a result, the trial solution of Eq. (4.2) can be expressed as follows:

$$r\left(\Theta \right)={\tau }_{0}+{\tau }_{1}\chi \left(\Theta \right)+{\sigma }_{1}\Pi (\Theta ).$$
(4.3)

Computing the estimation as per the asserted steps of methods, we obtain a number of solution depending on the values of parameter \(\lambda\), that are discussed in the successive context.

Class 1: When we attributed the condition \(\lambda <0\), the deduced values of the parameters are worked out as:

Set 1: \({\tau }_{0}=0\), \({\tau }_{1}=\pm \frac{\sqrt{6}\sqrt{a}\varrho }{\sqrt{b{\varrho }^{2}\lambda -2b}}\), \({\sigma }_{1}=\pm \frac{\sqrt{6}\sqrt{a}\varrho \sqrt{{\mu }^{2}+{\lambda }^{2}\Lambda }}{\sqrt{-\lambda }\sqrt{b{\varrho }^{2}\lambda -2b}}\), \(\Omega =-\frac{4a\varrho }{-2+{\varrho }^{2}\lambda }\).

Set 2: \({\tau }_{0}=0\), \({\tau }_{1}=\pm \frac{2\sqrt{3}\sqrt{a}\varrho }{\sqrt{2b{\varrho }^{2}\lambda -b}}\), \({\sigma }_{1}=0\), \(\mu =0\), \(\Omega =-\frac{2a\varrho }{-1+2{\varrho }^{2}\lambda }\).

Set 3: \({\tau }_{0}=0\), \({\tau }_{1}=0\), \({\sigma }_{1}=\pm \frac{2\sqrt{3}\sqrt{a}\varrho \sqrt{\lambda }\sqrt{\Lambda }}{\sqrt{b+b{\varrho }^{2}\lambda }}\), \(\mu =0\), \(\Omega =\frac{2a\varrho }{1+{\varrho }^{2}\lambda }\).

Introducing the estimated values of the parameters asserted above, the respective closed-form wave solutions can be obtained as:

$${w}_{11}\left(x,t\right)=\pm \frac{\sqrt{6}\sqrt{a}\varrho }{\sqrt{b{\varrho }^{2}\lambda -2b}\left(\frac{\mu }{\lambda }+\mathrm{sinh}(\Theta \sqrt{-\lambda }){\Upsilon }_{1}+\mathrm{cosh}(\Theta \sqrt{-\lambda }){\Upsilon }_{2}\right)}\Bigg\{\frac{\sqrt{{\mu }^{2}+{\lambda }^{2}\Lambda }}{\sqrt{-\lambda }}$$
$$-\sqrt{-\lambda }\left(\mathrm{cosh}\left(\Theta \sqrt{-\lambda }\right){\Upsilon }_{1}+\mathrm{sinh}\left(\Theta \sqrt{-\lambda }\right){\Upsilon }_{2}\right\},$$
(4.4)
$${w}_{12}\left(x,t\right)=\pm \frac{2\sqrt{3}\sqrt{a}\varrho \sqrt{-\lambda }(\mathrm{cosh}(\Theta \sqrt{-\lambda }){\Upsilon }_{1}+\mathrm{sinh}(\Theta \sqrt{-\lambda }){\Upsilon }_{2})}{\sqrt{2b{\varrho }^{2}\lambda -b}(\mathrm{sinh}(\Theta \sqrt{-\lambda }){\Upsilon }_{1}+\mathrm{cosh}(\Theta \sqrt{-\lambda }){\Upsilon }_{2})},$$
(4.5)
$${w}_{13}\left(x,t\right)=\pm \frac{2\sqrt{3}\sqrt{a}\varrho \sqrt{\lambda }\sqrt{\Lambda }}{\sqrt{b+b{\varrho }^{2}\lambda }(\mathrm{sinh}(\Theta \sqrt{-\lambda }){\Upsilon }_{1}+\mathrm{cosh}(\Theta \sqrt{-\lambda }){\Upsilon }_{2})},$$
(4.6)

where \(\Theta =\varrho x-\frac{\Omega {(t+\frac{1}{\Gamma \beta })}^{\beta }}{\beta }\), \(\Lambda ={\Upsilon }_{1}^{2}-{\Upsilon }_{2}^{2}\), and \({\Upsilon }_{1}\), \({\Upsilon }_{2}\) being free parameters.Setting \(\Upsilon {}_{2}, \mu =0\), the solution (4.4) takes the form as:

\({w}_{11}\left(x,t\right)=\pm \frac{\sqrt{6}\sqrt{a}\varrho \sqrt{-\lambda }}{\sqrt{b{\varrho }^{2}\lambda -2b}}\{\mathrm{csch}(\Theta \sqrt{-\lambda })-(\mathrm{coth}(\Theta \sqrt{-\lambda })\).

Correspondingly, the rest of the solutions can be transmuted to another form for the apted values of the parameters \({\Upsilon }_{1}\), \({\Upsilon }_{2}\), and \(\mu\).

Class 2: If we choose positive values for the parameter \(\lambda\), the implication of concerned approach to the Eq. (4.2) provides the following values of the parameters.

Set 1: \({\tau }_{0}=0\), \({\tau }_{1}=\pm \frac{\sqrt{6}\sqrt{a}\varrho }{\sqrt{b{\varrho }^{2}\lambda -2b}}\), \({\sigma }_{1}=\pm \frac{\sqrt{6}\sqrt{a{\varrho }^{2}{\lambda }^{2}\Lambda -a{\varrho }^{2}{\mu }^{2}}}{\sqrt{\lambda }\sqrt{b{\varrho }^{2}\lambda -2b}}\), \(\Omega =-\frac{4a\varrho }{-2+{\varrho }^{2}\lambda }\).

Set 2: \({\tau }_{0}=0\), \({\tau }_{1}=\pm \frac{2\sqrt{3}\sqrt{a}\varrho }{\sqrt{-(2b{\varrho }^{2}\lambda +b)}}\), \({\sigma }_{1}=0\), \(\mu =0\), \(\Omega =-\frac{2a\varrho }{-1+2{\varrho }^{2}\lambda }\).

Set 3: \({\tau }_{0}=0\), \({\tau }_{1}=0\), \({\sigma }_{1}=\pm \frac{2\sqrt{3}\sqrt{a}\varrho \sqrt{\lambda }\sqrt{\Lambda }}{\sqrt{-(b+b{\varrho }^{2}\lambda })}\), \(\mu =0\), \(\Omega =\frac{2a\varrho }{1+{\varrho }^{2}\lambda }\).

Putting into force the derived parametric values into the solution (4.3), the resultant solutions in this case can be written as:

$${w}_{21}=\pm \frac{\sqrt{6}\sqrt{a}\varrho }{\sqrt{b{\varrho }^{2}\uplambda -2\mathrm{b}}\left(\frac{\mu }{\lambda }+\mathrm{sin}(\Theta \sqrt{\lambda }){\Upsilon }_{1}+\mathrm{cos}(\Theta \sqrt{\lambda }){\Upsilon }_{2}\right)}\Bigg\{\frac{\sqrt{{\lambda }^{2}\Lambda -{\mu }^{2}}}{\sqrt{\lambda }}$$
$$\left.-\sqrt{\lambda }(\mathrm{cos}(\Theta \sqrt{\lambda }){\Upsilon }_{1}-\mathrm{sin}(\Theta \sqrt{\lambda }){\Upsilon }_{2})\right\}.$$
(4.7)
$${w}_{22}\left(x,t\right)=\pm \frac{2\sqrt{3}\sqrt{a}\varrho \sqrt{\lambda }(\mathrm{cos}(\Theta \sqrt{\lambda }){\Upsilon }_{1}-\mathrm{sin}(\Theta \sqrt{\lambda }){\Upsilon }_{2})}{\sqrt{2b{\varrho }^{2}\lambda -b}(\mathrm{sin}(\Theta \sqrt{\lambda }){\Upsilon }_{1}+\mathrm{cos}(\Theta \sqrt{\lambda }){\Upsilon }_{2})}.$$
(4.8)
$${w}_{23}\left(x,t\right)=\pm \frac{2\sqrt{3}\sqrt{a}\varrho \sqrt{\lambda }\sqrt{\Lambda }}{\sqrt{-(b+b{\varrho }^{2}\lambda )}(\mathrm{sin}(\Theta \sqrt{\lambda }){\Upsilon }_{1}+\mathrm{cos}(\Theta \sqrt{\lambda }){\Upsilon }_{2})}.$$
(4.9)

Here \(\Theta =\varrho x-\frac{\Omega {(t+\frac{1}{\Gamma \beta })}^{\beta }}{\beta }\), \(\Lambda ={\Upsilon }_{1}^{2}+{\Upsilon }_{2}^{2}\), and \({\Upsilon }_{1}\), \({\Upsilon }_{2}\) being free parameters.

Class 3: Analogously, the obtained parametric values for \(\lambda =0\) are provided below:

Set 1: \({\tau }_{0}=0\), \({\tau }_{1}=\pm \frac{\sqrt{3}\sqrt{a}\varrho }{\sqrt{-b}}\), \({\sigma }_{1}=\pm \frac{\sqrt{3}\sqrt{a}\varrho \sqrt{{\Upsilon }_{1}^{2}-2\mu {\Upsilon }_{2}}}{\sqrt{-b}}\), \(\Omega =2a\varrho\).

Set 2: \({\tau }_{0}=0\), \({\tau }_{1}=0\), \({\sigma }_{1}=\pm \frac{2\sqrt{3}\sqrt{a}\varrho {\Upsilon }_{1}}{\sqrt{-b}}\), \(\Omega =2a\varrho\), \(\mu =0\).

Set 3:\({\tau }_{0}=0\), \({\tau }_{1}=\pm \frac{2\sqrt{3}\sqrt{a}\varrho }{\sqrt{-b}}\), \({\sigma }_{1}=0\), \(\Omega =2a\varrho\), \(\mu =0\).

By setting the obtained parametric values into the solution (4.3), we can represent the resulting solutions in the following ways:

$${w}_{31}\left(x,t\right)=\pm \frac{\sqrt{3}\sqrt{a}\varrho \left(\Theta \mu +\Upsilon \right)}{\sqrt{-b}\left(\frac{{\Theta }^{2}\mu }{2}+\Theta {\Upsilon }_{1}+{\Upsilon }_{2}\right)}\left\{\left(\Theta \mu +{\Upsilon }_{1}\right)+\sqrt{{\Upsilon }_{1}^{2}-2\mu {\Upsilon }_{2}}\right\}.$$
(4.10)
$${w}_{32}\left(x,t\right)=\pm \frac{2\sqrt{3}\sqrt{a}\varrho {\Upsilon }_{1}}{\sqrt{-b}(\Theta {\Upsilon }_{1}+{\Upsilon }_{2})},$$
(4.11)

where \(\Theta =\varrho x-\frac{\Omega {(t+\frac{1}{\Gamma \beta })}^{\beta }}{\beta }\), and \({\Upsilon }_{1}\), \({\Upsilon }_{2}\) being free parameters.

It is possible to obtain other useful closed-form soliton solutions of the simplified modified CH equation by choosing different values of the free parameters; however, for conciseness, these particular solutions are not provided in detail in this context.

4 Comparison

In this section, we establish a comparison between the results obtained presently and the former results found in the literature using different analytical techniques. This comparison has been accomplished to emphasize the originality of this study, and the details can be found in the subsequent Table 1.

Table 1 Comparison of the results
Full size table

Reviewing the Table, it becomes evident that some of the results obtained in this article by appropriately selecting the parameter values are similar to some of the previous results. However, it should be noted that their original expression is different from ours. Despite conducting a thorough search across relevant articles that have investigated the equation under consideration, we could not find any other identical solution to the one we have obtained. Therefore, it is noteworthy that the remaining results we obtained are new and innovative, as they do not appear to have been previously documented.

5 Graphical representations and analysis

We have presented two- and three- dimensional plots of the solutions to enhance understanding of the characteristics of obtained solutions. Besides, the contour plots of solutions have been included to demonstrate the stability of solitons. These figures are plotted within the range of \(-10\le x\le 10\) and \(0\le t\le 10\). In the subsequent context, we have discussed the features and applications of the several useful solutions.

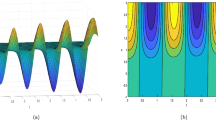
Figure 1 represents the absolute value of solution (4.4) which have been plotted for the values \(a=0.02\), \(\varrho =0.34\), \(\lambda =-10\), \(b=-8.18\), \(\beta =0.99\), \({\Upsilon }_{1}=-10.8\), \({\Upsilon }_{2}=13.7\), and \(\mu =5.15\). It can be observed from the figure that the absolute value of solution (4.4) describes a bell-shaped soliton for the chosen values of parameters. This type of soliton is also acquainted as the bright or non-topological soliton, and very useful in optical fiber study to transfer signals or data over a long distance. It provides a constant value for \(t\to \infty\). Shallow water waves typically involve the interaction of waves with a seafloor or coastline, and undergo shoaling, breaking, and dispersion due to the varying depth of the water. As bell-shaped can propagate a wide range without distortion, it has remarkable application to investigate wave natures in shallow water. The absolute value of solution (4.5) revels the anti-peakon soliton, which have been plotted in Fig. 2 for the values \(a=0.14\), \(\varrho =-0.08\), \(\lambda =-8.49\), \(b=2.06\), \(\beta =0.1\), \({\Upsilon }_{1}=-7.2\), \({\Upsilon }_{2}=15\), whereas the absolute value of solution (4.6) presents a singular bell-shaped soliton for the chosen values of parameter \(a=0.26\), \(\varrho =2.06\), \(\lambda =-0.99\), \(b=-0.36\), \(\beta =0.99\), \({\Upsilon }_{1}=-5.5\), \({\Upsilon }_{2}=12.45\) as shown in Fig. 3. In an anti-peakon soliton, the first-derivative becomes undefined at the lowest tough even though the function is continuous. On the other hand, singular bell-shaped soliton incorporates singularity and the function is discontinuous at the point \(x=0\). Anti-peakon is robust and efficient in data transmission system to transmit signal in remote area without any distortion. It is a special case of the anti-bell-shaped soliton.

Fig. 1
figure 1

a 3D, b 2D, and c contour plots of absolute value of solution (4.4)

Full size image
Fig. 2
figure 2

a 3D, b 2D, and c contour plots of absolute value of solution (4.5)

Full size image
Fig. 3
figure 3

Depiction of absolute value of solution (4.6)

Full size image

Figure 4 displays the graphical characteristics of the absolute value of solution (4.7), which have been plotted for the values \(a=-1.18\), \(\varrho =-0.17\), \(\lambda =0.1\), \(b=-0.08\), \(\beta =0.99\), \({\Upsilon }_{1}=10.45\), \({\Upsilon }_{2}=-11.35\), and \(\mu =13.8\). If we change the value of \(\varrho\) (wave number) to \(\varrho =-1.94\), it will represent a periodic soliton as shown in Fig. 5. Both of the solutions are useful to study the nonlinear wave property in shallow water wave. The periodic soliton is characterized by its periodic behavior, and the compacton is characterized by its compact seize. Thus, the periodic soliton travels a long distance having the unchanged velocity and shape, whereas compacton travels in a limited area.

Fig. 4
figure 4

Depiction of absolute value of solution (4.7)

Full size image
Fig. 5
figure 5

Depiction of absolute value of solution (4.7)

Full size image

The absolute value of solution (4.8) presents a singular periodic soliton for the values \(a=2.28\), \(\varrho =-0.56\), \(\lambda =0.1\), \(b=2.7\), \(\beta =0.99\), \({\Upsilon }_{1}=-2\), \({\Upsilon }_{2}=-10.3\), which has been attached in Fig. 6. Figure 7 is illustrated the absolute value of solution (4.10) which is plotted for the values \(a=-10\), \(\varrho =-10\), \(\lambda =0.1\), \(b=-0.1\), \(\beta =0.99\), \({\Upsilon }_{1}=1.45\), \({\Upsilon }_{2}=-12.05\), and \(\mu =-13.7\). The absolute value of solution (4.10) presents a flat kink soliton.

Fig. 6
figure 6

Depiction of absolute value of solution (4.8)

Full size image
Fig. 7
figure 7

Depiction of absolute value of solution (4.10)

Full size image

The study of soliton waves plays a role in coastal studies and the development of structures such as harbor entrances. By comprehending their behavior, it can effectively control wave energy and ensure the safety and stability of coastal infrastructure. Moreover, solitary waves are useful for simulating and understanding tsunami waves in shallow water. Since this study presents several new solutions to the concerned equation, these solutions might help to study the new properties of shallow water waves.

6 Conclusion

This article focuses on the investigation of the modified fractional Camassa-Holm equation using the \(({G}{\prime}/G, 1/G)\)-expansionapproach in order to establish a range of useful soliton solutions. The obtained solutions provide valuable insights into the characteristics and behavior of shallow water waves through various types of solitons, such as periodic, bell-shaped, compacton, anti-peakon, and singular bell-shaped solitons. These solutions are obtained by appropriately selecting parameter values within the analytical framework. The obtained solutions are visualized through three-dimensional, two-dimensional, and contour plots to aid in better comprehension. These findings have significant implications for the study of diverse physical phenomena, including fluid dynamics, coastal engineering, and other related fields. Moreover, the analytical solutions obtained offer potential insights into the behavior of shallow water waves, serving as a basis for further research in coastal engineering and tsunami waves.