Abstract
We consider parity games, a special form of two-player infinite-duration games on numerically labelled graphs, whose winning condition requires that the maximal value of a label occurring infinitely often during a play be of some specific parity. The problem has a rather intriguing status from a complexity theoretic viewpoint, since it belongs to the class  , and still open is the question whether it can be solved in polynomial time. Parity games also have great practical interest, as they arise in many fields of theoretical computer science, most notably logic, automata theory, and formal verification. In this paper, we propose a new algorithm for the solution of the problem, based on the idea of promoting vertices to higher priorities during the search for winning regions. The proposed approach has nice computational properties, exhibiting the best space complexity among the currently known solutions. Experimental results on both random games and benchmark families show that the technique is also very effective in practice.
, and still open is the question whether it can be solved in polynomial time. Parity games also have great practical interest, as they arise in many fields of theoretical computer science, most notably logic, automata theory, and formal verification. In this paper, we propose a new algorithm for the solution of the problem, based on the idea of promoting vertices to higher priorities during the search for winning regions. The proposed approach has nice computational properties, exhibiting the best space complexity among the currently known solutions. Experimental results on both random games and benchmark families show that the technique is also very effective in practice.
F. Mogavero—Sponsored by the Engineering and Physical Sciences Research Council of the United Kingdom, grant EP/M005852/1.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Parity games [45] are perfect-information two-player turn-based games of infinite duration, usually played on finite directed graphs. Their vertices, labelled by natural numbers called priorities, are assigned to one of two players, named Even and Odd or, simply, 0 and 1, respectively. The game starts at an arbitrary vertex and, during its evolution, each player can take a move only at its own positions, which consists in choosing one of the edges outgoing from the current vertex. The moves selected by the players induce an infinite sequence of vertices, called play. If the maximal priority of the vertices occurring infinitely often in the play is even, then the play is winning for player 0, otherwise, player 1 takes it all.
Parity games have been extensively studied in the attempt to find efficient solutions to the problem of determining the winner. From a complexity theoretic perspective, this decision problem lies in  [18, 19], since it is memoryless determined [17, 37, 38, 45]. It has been even proved to belong to
[18, 19], since it is memoryless determined [17, 37, 38, 45]. It has been even proved to belong to  [31], a status shared with the factorisation problem [1, 24, 25]. They are the simplest class of games in a wider family with similar complexities and containing, e.g., mean payoff games [16, 30], discounted payoff games [55], and simple stochastic games [15]. In fact, polynomial time reductions exist from parity games to the latter ones. However, despite being the most likely class among those games to admit a polynomial-time solution, the answer to the question whether such a solution exists still eludes the research community.
[31], a status shared with the factorisation problem [1, 24, 25]. They are the simplest class of games in a wider family with similar complexities and containing, e.g., mean payoff games [16, 30], discounted payoff games [55], and simple stochastic games [15]. In fact, polynomial time reductions exist from parity games to the latter ones. However, despite being the most likely class among those games to admit a polynomial-time solution, the answer to the question whether such a solution exists still eludes the research community.
The effort devoted to provide efficient solutions stems primarily form the fact that many problems in formal verification and synthesis can be reformulated in terms of solving parity games. Emerson, Jutla, and Sistla [18, 19] have shown that computing winning strategies for these games is linear-time equivalent to solving the modal \(\mu \textsc {Calculus}\) model checking problem [20]. Parity games also play a crucial role in automata theory [17, 36, 44], where, for instance, they can be applied to solve the complementation problem for alternating automata [29] and the emptiness of the corresponding nondeterministic tree automata [36]. These automata, in turn, can be used to solve the satisfiability and model checking problems for expressive logics, such as the modal [53] and alternating [2, 51] \(\mu \textsc {Calculus}\), \(\mathrm{ATL}^*\) [2, 50], Strategy Logic [14, 40, 41, 43], Substructure Temporal Logic [4, 5], and fixed-point extensions of guarded first-order logics [7, 8].
Previous solutions mainly divide into two families: those based on decomposing the game into subsets of winning regions, called dominions, and those trying to directly build winning strategies for the two players on the entire game. To the first family belongs the divide et impera solution originally proposed by McNaughton [39] for Muller games and adapted to parity games by Zielonka [54]. More recent improvements to that recursive algorithm have been proposed by Jurdziński, Paterson, and Zwick [33, 34] and by Schewe [48]. Both approaches rely on finding suitably closed dominions, which can then be removed from a game to reduce the size of the subgames to be recursively solved. To the second family belongs the procedure proposed by Jurdziński [32], which exploits the connection between the notions of progress measures [35] and winning strategies. An alternative approach was proposed by Jurdziński and Vöge [52], based on the idea of iteratively improving an initial non-winning strategy. This technique was later optimised by Schewe [49]. From a purely theoretical viewpoint, the best asymptotic behaviour obtained to date is the one exhibited by the solution proposed in [48], which runs in time  , where n and e are the number of vertices and edges of the underlying graph and k is the number of priorities. As far as space consumption is concerned, we have two incomparable best behaviours:
, where n and e are the number of vertices and edges of the underlying graph and k is the number of priorities. As far as space consumption is concerned, we have two incomparable best behaviours:  , for the small progress measure procedure of [32], and
, for the small progress measure procedure of [32], and  , for the optimised strategy improvement method of [49]. Due to their inherent recursive nature, the algorithms of the first family require
, for the optimised strategy improvement method of [49]. Due to their inherent recursive nature, the algorithms of the first family require  memory, which could be reduced to
memory, which could be reduced to  , by representing subgames implicitly through their sets of vertices. All these bounds do not seem to be amenable to further improvements, as they appear to be intrinsic to the corresponding solution techniques. Polynomial time solutions are only known for restricted versions of the problem, where one among the tree-width [22, 23, 46], the dag-width [6], the clique-width [47] and the entanglement [9] of the underlying graph is bounded.
, by representing subgames implicitly through their sets of vertices. All these bounds do not seem to be amenable to further improvements, as they appear to be intrinsic to the corresponding solution techniques. Polynomial time solutions are only known for restricted versions of the problem, where one among the tree-width [22, 23, 46], the dag-width [6], the clique-width [47] and the entanglement [9] of the underlying graph is bounded.
The main contribution of the paper is a new algorithm for solving parity games, based on the notions of quasi dominion and priority promotion. A quasi dominion Q for player \(\alpha \in \{ 0, 1 \}\), called a quasi \(\alpha \) -dominion, is a set of vertices from each of which player \(\alpha \) can enforce a winning play that never leaves the region, unless one of the following two conditions holds: (i) the opponent  can escape from Q or (ii) the only choice for player \(\alpha \) itself is to exit from Q (i.e., no edge from a vertex of \(\alpha \) remains in Q). Quasi dominions can be ordered by assigning to each of them a priority corresponding to an under-approximation of the best value the opponent can be forced to visit along any play exiting from it. A crucial property is that, under suitable and easy to check assumptions, a higher priority quasi \(\alpha \)-dominion \(\mathrm{Q}_1\) and a lower priority one \(\mathrm{Q}_2\), can be merged into a single quasi \(\alpha \)-dominion of the higher priority, thus improving the approximation for \(\mathrm{Q}_2\). For this reason we call this merging operation a priority promotion of \(\mathrm{Q}_2\) to \(\mathrm{Q}_1\). The underlying idea of our approach is to iteratively enlarge quasi \(\alpha \)-dominions, by performing sequences of promotions, until an \(\alpha \)-dominion is obtained.
can escape from Q or (ii) the only choice for player \(\alpha \) itself is to exit from Q (i.e., no edge from a vertex of \(\alpha \) remains in Q). Quasi dominions can be ordered by assigning to each of them a priority corresponding to an under-approximation of the best value the opponent can be forced to visit along any play exiting from it. A crucial property is that, under suitable and easy to check assumptions, a higher priority quasi \(\alpha \)-dominion \(\mathrm{Q}_1\) and a lower priority one \(\mathrm{Q}_2\), can be merged into a single quasi \(\alpha \)-dominion of the higher priority, thus improving the approximation for \(\mathrm{Q}_2\). For this reason we call this merging operation a priority promotion of \(\mathrm{Q}_2\) to \(\mathrm{Q}_1\). The underlying idea of our approach is to iteratively enlarge quasi \(\alpha \)-dominions, by performing sequences of promotions, until an \(\alpha \)-dominion is obtained.
We prove soundness and completeness of the algorithm. Moreover, a bound  on the time complexity and a
on the time complexity and a  bound on the memory requirements are provided. Experimental results, comparing our algorithm with the state of the art solvers, also show that the proposed approach perform very well in practice, most often significantly better than existing ones, on both random games and benchmark families proposed in the literature.
bound on the memory requirements are provided. Experimental results, comparing our algorithm with the state of the art solvers, also show that the proposed approach perform very well in practice, most often significantly better than existing ones, on both random games and benchmark families proposed in the literature.
2 Parity Games
Let us first briefly recall the notation and basic definitions concerning parity games that expert readers can simply skip. We refer to [3, 54] for a comprehensive presentation of the subject.
Given a partial function  we denote the domain and range of
we denote the domain and range of  , respectively.
, respectively.
A two-player turn-based arena is a tuple  , with
, with  and
and  , such that
, such that  is a finite directed graph.
is a finite directed graph.  (resp.
(resp.  ) is the set of positions of player 0 (resp., 1) and
) is the set of positions of player 0 (resp., 1) and  is a left-total relation describing all possible moves. A path in
is a left-total relation describing all possible moves. A path in  is a finite or infinite sequence
is a finite or infinite sequence  of positions in V compatible with the move relation, i.e.,
of positions in V compatible with the move relation, i.e.,  , for all
, for all  . For a finite path
. For a finite path  , with
, with  we denote the last position of
we denote the last position of  . A positional strategy for player \(\alpha \in \{ 0, 1 \}\) on
. A positional strategy for player \(\alpha \in \{ 0, 1 \}\) on  is a partial function
is a partial function  , mapping each \(\alpha \)-position
, mapping each \(\alpha \)-position  to position
to position  compatible with the move relation, i.e.,
compatible with the move relation, i.e.,  . With
. With  we denote the set of all \(\alpha \)-strategies on V. A play in
we denote the set of all \(\alpha \)-strategies on V. A play in  from a position
from a position  w.r.t. a pair of strategies
w.r.t. a pair of strategies  , called
, called  -play, is a path
-play, is a path  such that
such that  and, for all
and, for all  , if
, if  then
then  else
else  . The play function
. The play function  returns, for each position
returns, for each position  and pair of strategies
and pair of strategies  , the maximal
, the maximal  -play
-play  .
.
A parity game is a tuple  , where
, where  is an arena,
is an arena,  is a finite set of priorities, and
is a finite set of priorities, and  is a priority function assigning a priority to each position. The priority function can be naturally extended to games and paths as follows:
is a priority function assigning a priority to each position. The priority function can be naturally extended to games and paths as follows:  ; for a path
; for a path  , we set
, we set  , if
, if  is finite, and
is finite, and  , otherwise. A set of positions
, otherwise. A set of positions  is an \(\alpha \)-dominion, with \(\alpha \in \{ 0, 1 \}\), if there exists an \(\alpha \)-strategy
is an \(\alpha \)-dominion, with \(\alpha \in \{ 0, 1 \}\), if there exists an \(\alpha \)-strategy  such that, for all
such that, for all  -strategies
-strategies  and positions
and positions  , the induced play
, the induced play  is infinite and
is infinite and  . In other words,
. In other words,  only induces on V infinite plays whose maximal priority visited infinitely often has parity \(\alpha \). By
only induces on V infinite plays whose maximal priority visited infinitely often has parity \(\alpha \). By  we denote the maximal subgame of
we denote the maximal subgame of  with set of positions
with set of positions  contained in
contained in  and move relation
and move relation  equal to the restriction of
equal to the restriction of  to
to  .
.
The \(\alpha \)-predecessor of V, in symbols  , collects the positions from which player \(\alpha \) can force the game to reach some position in V with a single move. The \(\alpha \)-attractor
, collects the positions from which player \(\alpha \) can force the game to reach some position in V with a single move. The \(\alpha \)-attractor  generalizes the notion of \(\alpha \)-predecessor
generalizes the notion of \(\alpha \)-predecessor  to an arbitrary number of moves. Thus, it corresponds to the least fix-point of that operator. When
to an arbitrary number of moves. Thus, it corresponds to the least fix-point of that operator. When  , we say that V is \(\alpha \)-maximal. Intuitively, V is \(\alpha \)-maximal if player \(\alpha \) cannot force any position outside V to enter this set. For such a V, the set of positions of the subgame
, we say that V is \(\alpha \)-maximal. Intuitively, V is \(\alpha \)-maximal if player \(\alpha \) cannot force any position outside V to enter this set. For such a V, the set of positions of the subgame  is precisely
is precisely  . Finally, the \(\alpha \)
-escape of V, formally
. Finally, the \(\alpha \)
-escape of V, formally  , contains the positions in V from which \(\alpha \) can leave V in one move, while the dual notion of \(\alpha \)
-interior, defined as
, contains the positions in V from which \(\alpha \) can leave V in one move, while the dual notion of \(\alpha \)
-interior, defined as  , contains the \(\alpha \)-positions from which \(\alpha \) cannot escape with a single move.
, contains the \(\alpha \)-positions from which \(\alpha \) cannot escape with a single move.
3 A New Idea
A solution for a parity game  over an arena
over an arena  can trivially be obtained by iteratively computing dominions of some player, namely sets of positions from which that player has a strategy to win the game. Once an \(\alpha \)-dominion D for player \(\alpha \in \{ 0, 1 \}\) is found, its \(\alpha \)-attractor
can trivially be obtained by iteratively computing dominions of some player, namely sets of positions from which that player has a strategy to win the game. Once an \(\alpha \)-dominion D for player \(\alpha \in \{ 0, 1 \}\) is found, its \(\alpha \)-attractor  gives an \(\alpha \)-maximal dominion containing D, i.e., \(\alpha \) cannot force any position outside D to enter this set. The subgame
gives an \(\alpha \)-maximal dominion containing D, i.e., \(\alpha \) cannot force any position outside D to enter this set. The subgame  can then be solved by iterating the process. Therefore, the crucial problem to address consists in computing a dominion for some player in the game. The difficulty here is that, in general, no unique priority exists which satisfies the winning condition for a player along all the plays inside the dominion. In fact, that value depends on the strategy chosen by the opponent. Our solution to this problem is to proceed in a bottom-up fashion, starting from a weaker notion of \(\alpha \)-dominion, called quasi \(\alpha \)
-dominion. Then, we compose quasi \(\alpha \)-dominions until we obtain an \(\alpha \)-dominion. Intuitively, a quasi \(\alpha \)-dominion is a set of positions on which player \(\alpha \) has a strategy whose induced plays either remain in the set forever and are winning for \(\alpha \) or can exit from it. This notion is formalised by the following definition.
can then be solved by iterating the process. Therefore, the crucial problem to address consists in computing a dominion for some player in the game. The difficulty here is that, in general, no unique priority exists which satisfies the winning condition for a player along all the plays inside the dominion. In fact, that value depends on the strategy chosen by the opponent. Our solution to this problem is to proceed in a bottom-up fashion, starting from a weaker notion of \(\alpha \)-dominion, called quasi \(\alpha \)
-dominion. Then, we compose quasi \(\alpha \)-dominions until we obtain an \(\alpha \)-dominion. Intuitively, a quasi \(\alpha \)-dominion is a set of positions on which player \(\alpha \) has a strategy whose induced plays either remain in the set forever and are winning for \(\alpha \) or can exit from it. This notion is formalised by the following definition.
Definition 1
(Quasi Dominion). Let  be a game and \(\alpha \in \{ 0, 1 \}\) a player. A non-empty set of positions
be a game and \(\alpha \in \{ 0, 1 \}\) a player. A non-empty set of positions  is a quasi \(\alpha \)
-dominion in
is a quasi \(\alpha \)
-dominion in  if there exists an \(\alpha \)-strategy
if there exists an \(\alpha \)-strategy  such that, for all
such that, for all  -strategies
-strategies  , with
, with  , and positions \(v \in \mathrm{Q}\), the induced play
, and positions \(v \in \mathrm{Q}\), the induced play  satisfies
satisfies  , if
, if  is infinite, and
is infinite, and  , otherwise.
, otherwise.
The additional requirement that the opponent strategies be defined on all interior positions discards those strategies in which the opponent deliberately chooses to forfeit the play by declining to take any move at some of its positions.
We say that a quasi \(\alpha \)-dominion Q is \(\alpha \)
-open (resp., \(\alpha \)
-closed) if  (resp.,
(resp.,  ). In other words, in a closed quasi \(\alpha \)-dominion, player \(\alpha \) has a strategy whose induced plays are all infinite and winning. Hence, when closed, a quasi \(\alpha \)-dominion is a dominion for \(\alpha \) in
). In other words, in a closed quasi \(\alpha \)-dominion, player \(\alpha \) has a strategy whose induced plays are all infinite and winning. Hence, when closed, a quasi \(\alpha \)-dominion is a dominion for \(\alpha \) in  . The set of pairs
. The set of pairs  , where Q is a quasi \(\alpha \)-dominion, is denoted by
, where Q is a quasi \(\alpha \)-dominion, is denoted by  , and is partitioned into the sets
, and is partitioned into the sets  and
and  of open and closed quasi \(\alpha \)-dominion pairs, respectively.
of open and closed quasi \(\alpha \)-dominion pairs, respectively.
Note that quasi \(\alpha \)-dominions are loosely related with the concept of snares, introduced in [21] and used for completely different purposes, namely to speed up the convergence of strategy improvement algorithms.
During the search for a dominion, we explore a suitable partial order, whose elements, called states, record information about the open quasi dominions computed so far. The search starts from the top element, where the quasi dominions are initialised to the sets of nodes with the same priority. At each step, a query is performed on the current state to extract a new quasi dominion, which is then used to compute a successor state, if it is open. If, on the other hand, it is closed, the search is over. Different query and successor operations can in principle be defined, even on the same partial order. However, such operations cannot be completely independent. To account for this intrinsic dependence, we introduce a compatibility relation between states and quasi dominions that can be extracted by the query operation. Such a relation also forms the domain of the successor function. The partial order together with the query and successor operations and the compatibility relation forms what we call a dominion space.
Definition 2
(Dominion Space). A dominion space for a game  is a tuple
is a tuple  , where (1)
, where (1)  is a well-founded partial order w.r.t.
is a well-founded partial order w.r.t.  with distinguished element
with distinguished element  , (2)
, (2)  is the compatibility relation, (3)
is the compatibility relation, (3)  is the query function mapping each element
is the query function mapping each element  to a quasi dominion pair
to a quasi dominion pair  such that, if
such that, if  then
then  , and (4)
, and (4)  is the successor function mapping each pair
is the successor function mapping each pair  to the element
to the element  with
with  .
.
The depth of a dominion space \(\mathcal {D}\) is the length of the longest chain in the underlying partial order \(\mathcal {S}\) starting from \(\top \). Instead, by execution depth of \(\mathcal {D}\) we mean the length of the longest chain induced by the successor function  . Obviously, the execution depth is always bound by the depth.
. Obviously, the execution depth is always bound by the depth.
Different dominion spaces can be associated to the same game. Therefore, in the rest of this section, we shall simply assume a function \(\varGamma \) mapping every game  to a dominion space
to a dominion space  . Given the top element of
. Given the top element of  , Algorithm 1 searches for a dominion of either one of the two players by querying the current state
, Algorithm 1 searches for a dominion of either one of the two players by querying the current state  for a region pair \((\mathrm{Q}, \alpha )\). If this is closed in
for a region pair \((\mathrm{Q}, \alpha )\). If this is closed in  , it is returned as an \(\alpha \)-dominion. Otherwise, a successor state
, it is returned as an \(\alpha \)-dominion. Otherwise, a successor state  is computed and the search proceeds recursively from it. Clearly, since the partial order is well-founded, termination of the
is computed and the search proceeds recursively from it. Clearly, since the partial order is well-founded, termination of the  procedure is guaranteed. The total number of recursive calls is, therefore, the execution depth
procedure is guaranteed. The total number of recursive calls is, therefore, the execution depth  of the dominion space \(\mathcal {D}\), where n, e, and k are the number of positions, moves, and priorities, respectively. Hence,
of the dominion space \(\mathcal {D}\), where n, e, and k are the number of positions, moves, and priorities, respectively. Hence,  runs in time
runs in time  , where
, where  and
and  denote the time needed by the query and successor functions, respectively. Thus, the total time to solve a game is
denote the time needed by the query and successor functions, respectively. Thus, the total time to solve a game is  . Since the query and successor functions of the dominion space considered in the rest of the paper can be computed in linear time w.r.t. both n and e, the whole procedure terminates in time
. Since the query and successor functions of the dominion space considered in the rest of the paper can be computed in linear time w.r.t. both n and e, the whole procedure terminates in time  . As to the space requirements, observe that
. As to the space requirements, observe that  is a tail recursive algorithm. Hence, the upper bound on memory only depends on the space needed to encode the states of a dominion space, namely
is a tail recursive algorithm. Hence, the upper bound on memory only depends on the space needed to encode the states of a dominion space, namely  , where
, where  is the size of the partial order \(\mathcal {S}\) associated with \(\mathcal {D}\).
is the size of the partial order \(\mathcal {S}\) associated with \(\mathcal {D}\).

Soundness of the approach follows from the observation that quasi \(\alpha \)-dominions closed in the entire game are winning for player \(\alpha \) and so are their \(\alpha \)-attractors. Completeness, instead, is ensured by the nature of dominion spaces. Indeed, algorithm  always terminates by well-foundedness of the underlying partial order and, when it eventually does, a dominion for some player is returned. Therefore, the correctness of the algorithm reduces to proving the existence of a suitable dominion space, which is the subject of the next section.
always terminates by well-foundedness of the underlying partial order and, when it eventually does, a dominion for some player is returned. Therefore, the correctness of the algorithm reduces to proving the existence of a suitable dominion space, which is the subject of the next section.
4 Priority Promotion
In order to compute dominions, we shall consider a restricted form of quasi dominions that constrains the escape set to have the maximal priority in the game. Such quasi dominions are called regions.
Definition 3
(Region). A quasi \(\alpha \)-dominion R is an \(\alpha \)-region if  and all the positions in
and all the positions in  have priority
have priority  , i.e.
, i.e.  .
.
As a consequence of the above definition, if the opponent  can escape from an \(\alpha \)-region, it must visit a position with the highest priority in the region, which is of parity \(\alpha \). Similarly to the case of quasi dominions, we shall denote with
can escape from an \(\alpha \)-region, it must visit a position with the highest priority in the region, which is of parity \(\alpha \). Similarly to the case of quasi dominions, we shall denote with  the set of region pairs in
the set of region pairs in  and with
and with  and
and  the sets of open and closed region pairs, respectively. A closed \(\alpha \)-region is clearly an \(\alpha \)-dominion.
the sets of open and closed region pairs, respectively. A closed \(\alpha \)-region is clearly an \(\alpha \)-dominion.
At this point, we have all the tools to explain the crucial steps underlying the search procedure. Open regions are not winning, as the opponent can force plays exiting from them. Therefore, in order to build a dominion starting from open regions, we look for a suitable sequence of regions that can be merged together until a closed one is found. Obviously, the merging operation needs to be applied only to regions belonging to the same player, in such a way that the resulting set of position is still a region of that player. To this end, a mechanism is proposed, where an \(\alpha \)-region R in some game  and an \(\alpha \)-dominion D in a subgame of
and an \(\alpha \)-dominion D in a subgame of  not containing R itself are merged together, if the only moves exiting from
not containing R itself are merged together, if the only moves exiting from  -positions of D in the entire game lead to higher priority \(\alpha \)-regions and R has the lowest priority among them. As we shall see, this ensures that the new region
-positions of D in the entire game lead to higher priority \(\alpha \)-regions and R has the lowest priority among them. As we shall see, this ensures that the new region  has the same associated priority as R. This merging operation, based on the following proposition, is called promotion of the lower region to the higher one.
has the same associated priority as R. This merging operation, based on the following proposition, is called promotion of the lower region to the higher one.
Proposition 1
(Region Merging). Let  be a game,
be a game,  an \(\alpha \)-region, and
an \(\alpha \)-region, and  an \(\alpha \)-dominion in the subgame
an \(\alpha \)-dominion in the subgame  . Then,
. Then,  is an \(\alpha \)-region in
is an \(\alpha \)-region in  . Moreover, if both R and D are \(\alpha \)-maximal in
. Moreover, if both R and D are \(\alpha \)-maximal in  and
and  , respectively, then
, respectively, then  is \(\alpha \)-maximal in
is \(\alpha \)-maximal in  as well.
as well.
Proof
Since R is an \(\alpha \)-region, there is an \(\alpha \)-strategy  such that, for all
such that, for all  -strategies
-strategies  , with
, with  , and positions
, and positions  , the play induced by the two strategies is either winning for \(\alpha \) or exits from R passing through a position of the escape set
, the play induced by the two strategies is either winning for \(\alpha \) or exits from R passing through a position of the escape set  , which must be one of the position of maximal priority in
, which must be one of the position of maximal priority in  and of parity \(\alpha \). Set D is, instead, an \(\alpha \)-dominion in the game
and of parity \(\alpha \). Set D is, instead, an \(\alpha \)-dominion in the game  , therefore an \(\alpha \)-strategy
, therefore an \(\alpha \)-strategy  exists that is winning for \(\alpha \) from every position in D, regardless of the strategy
exists that is winning for \(\alpha \) from every position in D, regardless of the strategy  , with
, with  , chosen by the opponent
, chosen by the opponent  . To show that
. To show that  is an \(\alpha \)-region, it suffices to show that the following three conditions hold: (i) it is a quasi \(\alpha \)-dominion; (ii) the maximal priority of
is an \(\alpha \)-region, it suffices to show that the following three conditions hold: (i) it is a quasi \(\alpha \)-dominion; (ii) the maximal priority of  is of parity \(\alpha \); (iii) the escape set
is of parity \(\alpha \); (iii) the escape set  is contained in
is contained in  .
.
Condition (ii) immediately follows from the assumption that R is an \(\alpha \)-region in  . To show that also Condition (iii) holds, we observe that, since D is an \(\alpha \)-dominion in
. To show that also Condition (iii) holds, we observe that, since D is an \(\alpha \)-dominion in  , the only possible moves exiting from
, the only possible moves exiting from  -positions of D in game
-positions of D in game  must lead to R, i.e.,
must lead to R, i.e.,  . Hence, the only escaping positions of
. Hence, the only escaping positions of  , if any, must belong to R, i.e.
, if any, must belong to R, i.e.  . Since R is an \(\alpha \)-region in
. Since R is an \(\alpha \)-region in  , it hods that
, it hods that  . By transitivity, we conclude that
. By transitivity, we conclude that  .
.
Let us now consider Condition (i) and let the \(\alpha \)-strategy  be defined as the union of the two strategies above. Note that, being D and R disjoint sets of positions,
be defined as the union of the two strategies above. Note that, being D and R disjoint sets of positions,  is a well-defined strategy. We have to show that every path \(\pi \) compatible with
is a well-defined strategy. We have to show that every path \(\pi \) compatible with  and starting from a position in
and starting from a position in  is either winning for \(\alpha \) or ends in a position of the escape set
is either winning for \(\alpha \) or ends in a position of the escape set  .
.
First, observe that  contains only those positions in the escaping set of R from which \(\alpha \) cannot force to move into D, i.e.
contains only those positions in the escaping set of R from which \(\alpha \) cannot force to move into D, i.e.  .
.
Let now \(\pi \) be a play compatible with  . If \(\pi \) is an infinite play, then it remains forever in
. If \(\pi \) is an infinite play, then it remains forever in  and we have three possible cases. If \(\pi \) eventually remains forever in D, then it is clearly winning for \(\alpha \), since
and we have three possible cases. If \(\pi \) eventually remains forever in D, then it is clearly winning for \(\alpha \), since  coincides with
coincides with  on all the positions in D. Similarly, if \(\pi \) eventually remains forever in R, then it is also winning for \(\alpha \), as
on all the positions in D. Similarly, if \(\pi \) eventually remains forever in R, then it is also winning for \(\alpha \), as  coincides with
coincides with  on all the positions in R. If, on the other hand, \(\pi \) passes infinitely often through both R and D, it necessarily visits infinitely often an escaping position in
on all the positions in R. If, on the other hand, \(\pi \) passes infinitely often through both R and D, it necessarily visits infinitely often an escaping position in  , which has the maximal priority in
, which has the maximal priority in  and is of parity \(\alpha \). Hence, the parity of the maximal priority visited infinitely often along \(\pi \) is \(\alpha \) and \(\pi \) is winning for player \(\alpha \). Finally, if \(\pi \) is a finite play, then it must end at some escaping position of R from where \(\alpha \) cannot force to move to a position still in
and is of parity \(\alpha \). Hence, the parity of the maximal priority visited infinitely often along \(\pi \) is \(\alpha \) and \(\pi \) is winning for player \(\alpha \). Finally, if \(\pi \) is a finite play, then it must end at some escaping position of R from where \(\alpha \) cannot force to move to a position still in  , i.e., it must end in a position of the set
, i.e., it must end in a position of the set  . Therefore,
. Therefore,  . We can then conclude that
. We can then conclude that  also satisfies Condition (i).
also satisfies Condition (i).
Let us now assume, by contradiction, that  is not \(\alpha \)-maximal. Then, there must be at least one position v belonging to
is not \(\alpha \)-maximal. Then, there must be at least one position v belonging to  , from which \(\alpha \) can force entering
, from which \(\alpha \) can force entering  in one move. Assume first that v is an \(\alpha \)-position. Then there is a move from v leading either to R or to D. But this means that v belongs to either
in one move. Assume first that v is an \(\alpha \)-position. Then there is a move from v leading either to R or to D. But this means that v belongs to either  or
or  , contradicting \(\alpha \)-maximality of those sets. If v is a
, contradicting \(\alpha \)-maximality of those sets. If v is a  -position, instead, all its outgoing moves must lead to \(\mathrm{R} \cup \mathrm{D}\). If all those moves lead to R, then
-position, instead, all its outgoing moves must lead to \(\mathrm{R} \cup \mathrm{D}\). If all those moves lead to R, then  , contradicting \(\alpha \)-maximality of R in
, contradicting \(\alpha \)-maximality of R in  . If not, then in the subgame
. If not, then in the subgame  , the remaining moves from v must all lead to D. But then,
, the remaining moves from v must all lead to D. But then,  , contradicting \(\alpha \)-maximality of D in
, contradicting \(\alpha \)-maximality of D in  .
.
During the search, we keep track of the computed regions by means of an auxiliary priority function  , called region function, which formalises the intuitive notion of priority of a region described above. Initially, the region function coincides with the priority function
, called region function, which formalises the intuitive notion of priority of a region described above. Initially, the region function coincides with the priority function  of the entire game
of the entire game  . Priorities are considered starting from the highest one. A region of the same parity \(\alpha \in \{ 0, 1 \}\) of the priority p under consideration is extracted from the region function, by collecting the set of positions
. Priorities are considered starting from the highest one. A region of the same parity \(\alpha \in \{ 0, 1 \}\) of the priority p under consideration is extracted from the region function, by collecting the set of positions  . Then, its attractor
. Then, its attractor  is computed w.r.t. the subgame
is computed w.r.t. the subgame  , which is derived from
, which is derived from  by removing the regions with priority higher than p. The resulting set forms an \(\alpha \)-maximal set of positions from which the corresponding player can force a visit to positions with priority p. This first phase is called region extension. If the \(\alpha \)-region R is open in
by removing the regions with priority higher than p. The resulting set forms an \(\alpha \)-maximal set of positions from which the corresponding player can force a visit to positions with priority p. This first phase is called region extension. If the \(\alpha \)-region R is open in  , we proceed and process the next priority. In this case, we set the priority of the newly computed region to p. Otherwise, one of two situations may arise. Either R is closed in the whole game
, we proceed and process the next priority. In this case, we set the priority of the newly computed region to p. Otherwise, one of two situations may arise. Either R is closed in the whole game  or the only
or the only  -moves exiting from R lead to higher regions of the same parity. In the former case, R is a \(\alpha \)-dominion in the entire game and the search stops. In the latter case, R is only an \(\alpha \)-dominion in the subgame
-moves exiting from R lead to higher regions of the same parity. In the former case, R is a \(\alpha \)-dominion in the entire game and the search stops. In the latter case, R is only an \(\alpha \)-dominion in the subgame  , and a promotion of R to a higher region
, and a promotion of R to a higher region  can be performed, according to Proposition 1. The search, then, restarts from the priority of
can be performed, according to Proposition 1. The search, then, restarts from the priority of  , after resetting to the original priorities in
, after resetting to the original priorities in  all the positions of the lower priority regions. The region
all the positions of the lower priority regions. The region  resulting from the union of
resulting from the union of  and R will then be reprocessed and, possibly, extended in order to make it \(\alpha \)-maximal. If R can be promoted to more than one region, the one with the lowest priority is chosen, so as to ensure the correctness of the merging operation. Due to the property of maximality, no
and R will then be reprocessed and, possibly, extended in order to make it \(\alpha \)-maximal. If R can be promoted to more than one region, the one with the lowest priority is chosen, so as to ensure the correctness of the merging operation. Due to the property of maximality, no  -moves from R to higher priority
-moves from R to higher priority  -regions exist. Therefore, only regions of the same parity are considered in the promotion step. The correctness of region extension operation above, the remaining fundamental step in the proposed approach, is formalised by the following proposition.
-regions exist. Therefore, only regions of the same parity are considered in the promotion step. The correctness of region extension operation above, the remaining fundamental step in the proposed approach, is formalised by the following proposition.
Proposition 2
(Region Extension). Let  be a game and
be a game and  an \(\alpha \)-region in
an \(\alpha \)-region in  . Then,
. Then,  is an \(\alpha \)-maximal \(\alpha \)-region in
is an \(\alpha \)-maximal \(\alpha \)-region in  .
.
Proof
Since  is an \(\alpha \)-region in
is an \(\alpha \)-region in  , then the maximal priority in
, then the maximal priority in  is of parity \(\alpha \) and
is of parity \(\alpha \) and  . Hence, any position v in
. Hence, any position v in  must have priority
must have priority  . Player \(\alpha \) can force entering
. Player \(\alpha \) can force entering  from every position in
from every position in  , with a finite number of moves. Moreover,
, with a finite number of moves. Moreover,  is a quasi \(\alpha \)-dominion and the priorities of the positions in
is a quasi \(\alpha \)-dominion and the priorities of the positions in  are lower than or equal to
are lower than or equal to  . Hence, every play that remains in R forever either eventually remains forever in
. Hence, every play that remains in R forever either eventually remains forever in  and is winning for \(\alpha \), or passes infinitely often through
and is winning for \(\alpha \), or passes infinitely often through  and
and  . In the latter case, that path must visit infinitely often a position in
. In the latter case, that path must visit infinitely often a position in  that has the maximal priority in
that has the maximal priority in  and has parity \(\alpha \). Hence, the play is winning for \(\alpha \). If, on the other hand,
and has parity \(\alpha \). Hence, the play is winning for \(\alpha \). If, on the other hand,  can force a play to exit from R, it can do so only by visiting some position in
can force a play to exit from R, it can do so only by visiting some position in  . In other words,
. In other words,  . In either case, we conclude that R is an \(\alpha \)-region in
. In either case, we conclude that R is an \(\alpha \)-region in  . Finally, being R the result of an \(\alpha \)-attractor, it is clearly \(\alpha \)-maximal.
. Finally, being R the result of an \(\alpha \)-attractor, it is clearly \(\alpha \)-maximal.
Figure 1 and Table 1 illustrate the search procedure on an example game, where diamond shaped positions belong to player 0 and square shaped ones to the opponent 1. Player 0 wins from every position, hence the 0-region containing all the positions is a 0-dominion in this case. Each cell of the table contains a computed region. A downward arrow denotes a region that is open in the subgame where it is computed, while an upward arrow means that the region gets to be promoted to the priority in the subscript. The index of each row corresponds to the priority of the region. Following the idea sketched above, the first region obtained is the single-position 0-region \(\{ \texttt {a} \}\), which is open because of the two moves leading to d and e. At priority 5, the open 1-region \(\{ {\texttt {b}}, {\texttt {f}}, {\texttt {h}} \}\) is formed by attracting both f and h to b, which is open in the subgame where \(\{ {\texttt {a}} \}\) is removed. Similarly, the 0-region \(\{ {\texttt {c}} \}\) at priority 4 and the 1-region \(\{ {\texttt {d}} \}\) at priority 3 are open, once removed \(\{ {\texttt {a}}, {\texttt {b}}, {\texttt {f}}, {\texttt {h}} \}\) and \(\{ {\texttt {a}}, {\texttt {b}}, {\texttt {c}}, {\texttt {f}}, {\texttt {h}} \}\), respectively, from the game. At priority 2, the 0-region \(\{ {\texttt {e}} \}\) is closed in the corresponding subgame. However, it is not closed in the whole game, since it has a move leading to c, i.e., to region 4. A promotion of \(\{ {\texttt {e}} \}\) to 4 is then performed, resulting in the new 0-region \(\{ {\texttt {c}}, {\texttt {e}} \}\). The search resumes at the corresponding priority and, after computing the extension of such a region via the attractor, we obtain that it is still open in the corresponding subgame. Consequently, the 1-region of priority 3 is recomputed and, then, priority 1 is processed to build the 1-region \(\{ {\texttt {g}} \}\). The latter is closed in the associated subgame, but not in the original game, because of a move leading to position d. Hence, another promotion is performed, leading to closed region in Row 3 and Column 3, which in turn triggers a promotion to 5. Observe that every time a promotion to a higher region is performed, all positions of the regions at lower priorities are reset to their original priorities. The iteration of the region forming and promotion steps proceeds until the configuration in Column 7 is reached. Here only two 0-regions are present: the open region 6 containing \(\{ {\texttt {a}}, {\texttt {b}}, {\texttt {d}}, {\texttt {g}}, {\texttt {i}} \}\) and the closed region 4 containing \(\{ {\texttt {c}}, {\texttt {e}}, {\texttt {f}}, {\texttt {h}} \}\). The second one has a move leading to the first one, hence, it is promoted to its priority. This last operation forms a 0-region containing all the positions of the game. It is obviously closed in the whole game and is, therefore, a 0-dominion.
Note that, the positions in 0-region \(\{ {\texttt {c}}, {\texttt {e}} \}\) are reset to their initial priorities, when 1-region \(\{ {\texttt {d}}, {\texttt {g}} \}\) in Column 3 is promoted to 5. Similarly, when 0-region \(\{ {\texttt {i}} \}\) in Column 5 is promoted to 6, the priorities of the positions in both regions \(\{ {\texttt {b}}, {\texttt {d}}, {\texttt {f}}, {\texttt {g}}, {\texttt {h}} \}\) and \(\{ {\texttt {c}}, {\texttt {e}} \}\), highlighted by the grey areas, are reset. This is actually necessary for correctness, at least in general. In fact, if region \(\{ {\texttt {b}}, {\texttt {d}}, {\texttt {f}}, {\texttt {g}}, {\texttt {h}} \}\) were not reset, the promotion of \(\{ {\texttt {i}} \}\) to 6, which also attracts b, d, and g, would leave \(\{ {\texttt {f}}, {\texttt {h}} \}\) as a 1-region of priority 5. However, according to Definition 3, this is not a 1-region. Even worse, it would also be considered a closed 1-region in the entire game, without being a 1-dominion, since it is actually an open 0-region. This shows that, in principle, promotions to an higher priority require the reset of previously built regions of lower priorities.
In the rest of this section, we shall formalise the intuitive idea described above. The necessary conditions under which promotion operations can be applied are also stated. Finally, query and successor algorithms are provided, which ensure that the necessary conditions are easy to check and always met when promotions are performed.
The PP Dominion Space. In order to define the dominion space induced by the priority-promotion mechanism (PP, for short), we need to introduce some additional notation. Given a priority function  and a priority
and a priority  , we denote by
, we denote by  (resp.,
(resp.,  and
and  ) the function obtained by restricting the domain of r to the positions with priority greater than or equal to p (resp., greater than and lower than p). Formally,
) the function obtained by restricting the domain of r to the positions with priority greater than or equal to p (resp., greater than and lower than p). Formally,  ,
,  , and
, and  . By
. By  we denote the largest subgame contained in the structure
we denote the largest subgame contained in the structure  , which is obtained by removing from
, which is obtained by removing from  all the positions in the domain of
all the positions in the domain of  .
.
A priority function  in
in  is a region function iff, for all priorities
is a region function iff, for all priorities  with
with  , it holds that
, it holds that  is an \(\alpha \)-region in the subgame
is an \(\alpha \)-region in the subgame  , if non-empty. In addition, we say that r is maximal above
, if non-empty. In addition, we say that r is maximal above  iff, for all
iff, for all  with
with  , we have that
, we have that  is \(\alpha \)-maximal in
is \(\alpha \)-maximal in  with
with  .
.
To account for the current status of the search of a dominion, the states s of the corresponding dominion space need to contain the current region function r and the current priority p reached by the search in  . To each of such states
. To each of such states  , we then associate the subgame at s defined as
, we then associate the subgame at s defined as  , representing the portion of the original game that still has to be processed.
, representing the portion of the original game that still has to be processed.
We can now formally define the Priority Promotion dominion space, by characterising the corresponding state space and compatibility relation. Moreover, algorithms for the query and successor functions of that space are provided.
Definition 4
(State Space). A state space is a tuple  , where its components are defined as prescribed in the following:
, where its components are defined as prescribed in the following:
-
1.
 is the set of all pairs
is the set of all pairs  , called states, composed of a region function
, called states, composed of a region function  and a priority
and a priority  such that (a) r is maximal above p and (b)
such that (a) r is maximal above p and (b)  , and (c)
, and (c) 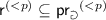 ;
; -
2.
 ;
; -
3.
for any two states
 , it holds that
, it holds that 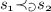 iff either (a) there exists a priority
iff either (a) there exists a priority  with
with  such that (a.i)
such that (a.i) 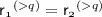 and (a.ii)
and (a.ii) 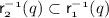 , or (b) both (b.i)
, or (b) both (b.i)  and (b.ii)
and (b.ii)  hold.
hold.
The state space specifies the configurations in which the priority promotion procedure can reside and the relative order that the successor function must satisfy. In particular, for a given state  , every region
, every region  , with priority
, with priority  , recorded in the region function r has to be \(\alpha \)-maximal, where
, recorded in the region function r has to be \(\alpha \)-maximal, where  . This implies that
. This implies that  . Moreover, the current priority p of the state must be the priority of an actual region in r. As far as the order is concerned, a state
. Moreover, the current priority p of the state must be the priority of an actual region in r. As far as the order is concerned, a state  is strictly smaller than another state
is strictly smaller than another state  if either there is a region recorded in
if either there is a region recorded in  at some higher priority that strictly contains the corresponding one in
at some higher priority that strictly contains the corresponding one in  and all regions above are equal in the two states, or state
and all regions above are equal in the two states, or state  is currently processing a lower priority than the one of
is currently processing a lower priority than the one of  .
.

At this point, we can determine the regions that are compatible with a given state. They are the only ones that the query function is allowed to return and that can then be used by the successor function to make the search progress in the dominion space. Intuitively, a region pair \((\mathrm{R}, \alpha )\) is compatible with a state  if it is an \(\alpha \)-region in the current subgame
if it is an \(\alpha \)-region in the current subgame  . Moreover, if such region is \(\alpha \)-open in that game, it has to be \(\alpha \)-maximal, and it has to necessarily contain the current region
. Moreover, if such region is \(\alpha \)-open in that game, it has to be \(\alpha \)-maximal, and it has to necessarily contain the current region  of priority p in r. These three accessory properties ensure that the successor function is always able to cast R inside the current region function r and obtain a new state.
of priority p in r. These three accessory properties ensure that the successor function is always able to cast R inside the current region function r and obtain a new state.
Definition 5
(Compatibility Relation). An open quasi dominion pair  is compatible with a state
is compatible with a state  , in symbols
, in symbols  , iff (1)
, iff (1)  and (2) if R is \(\alpha \)-open in
and (2) if R is \(\alpha \)-open in  then (2.a) R is \(\alpha \)-maximal in
then (2.a) R is \(\alpha \)-maximal in  and (2.b)
and (2.b)  .
.
Algorithm 2 provides a possible implementation for the query function compatible with the priority-promotion mechanism. Let  be the current state. Line 1 simply computes the parity \(\alpha \) of the priority to process in that state. Line 2, instead, computes in game
be the current state. Line 1 simply computes the parity \(\alpha \) of the priority to process in that state. Line 2, instead, computes in game  the attractor w.r.t. player \(\alpha \) of the region contained in r at the current priority p. The resulting set R is, according to Proposition 2, an \(\alpha \)-maximal \(\alpha \)-region in
the attractor w.r.t. player \(\alpha \) of the region contained in r at the current priority p. The resulting set R is, according to Proposition 2, an \(\alpha \)-maximal \(\alpha \)-region in  containing
containing  .
.
Before continuing with the description of the implementation of the successor function, we need to introduce the notion of best escape priority for player  w.r.t. an \(\alpha \)-region R of the subgame
w.r.t. an \(\alpha \)-region R of the subgame  and a region function r in the whole game
and a region function r in the whole game  . Informally, such a value represents the best priority associated with an \(\alpha \)-region contained in r and reachable by
. Informally, such a value represents the best priority associated with an \(\alpha \)-region contained in r and reachable by  when escaping from r. To formalise this concept, let
when escaping from r. To formalise this concept, let  be the interface relation between R and r, i.e., the set of
be the interface relation between R and r, i.e., the set of  -moves exiting from R and reaching some position within a region recorded in r. Then,
-moves exiting from R and reaching some position within a region recorded in r. Then,  is set to the minimal priority among those regions containing positions reachable by a move in I. Formally,
is set to the minimal priority among those regions containing positions reachable by a move in I. Formally,  . Note that, if R is a closed \(\alpha \)-region in
. Note that, if R is a closed \(\alpha \)-region in  , then
, then  is necessarily of parity \(\alpha \) and greater than the priority p of R. This property immediately follows from the maximality of r above p in any state of the dominion space. Indeed, no move of an
is necessarily of parity \(\alpha \) and greater than the priority p of R. This property immediately follows from the maximality of r above p in any state of the dominion space. Indeed, no move of an  -position can lead to a
-position can lead to a  -maximal
-maximal  -region. For instance, in the example of Fig. 1, for 0-region \(\mathrm{R} = \{{\texttt {e}}, {\texttt {f}}, {\texttt {h}}\}\) with priority equal to 2 in column 6, we have that \(I = \{({\texttt {e}},{\texttt {c}}),({\texttt {h}},{\texttt {b}})\}\) and
-region. For instance, in the example of Fig. 1, for 0-region \(\mathrm{R} = \{{\texttt {e}}, {\texttt {f}}, {\texttt {h}}\}\) with priority equal to 2 in column 6, we have that \(I = \{({\texttt {e}},{\texttt {c}}),({\texttt {h}},{\texttt {b}})\}\) and  . Hence,
. Hence,  .
.

In the following, to reset the priority of some the positions in the game, after a promotion of a given region is performed, we define the completing operator  that, taken a partial function
that, taken a partial function  and a total function \(\texttt {g} : \mathrm{A} \rightarrow \mathrm{B}\), returns the total function
and a total function \(\texttt {g} : \mathrm{A} \rightarrow \mathrm{B}\), returns the total function  . The result is equal to f on its domain and assumes the same values of g on the remaining part of the set A.
. The result is equal to f on its domain and assumes the same values of g on the remaining part of the set A.
Algorithm 3 implements the successor function informally described at the beginning of the section. Given the current state s and a compatible region pair \((\mathrm{R}, \alpha )\) open in the whole game as inputs, it produces a successor state  in the dominion space. It first checks whether R is open also in the subgame
in the dominion space. It first checks whether R is open also in the subgame  (Line 1). If this is the case, it assigns priority p to region R and stores it in the new region function
(Line 1). If this is the case, it assigns priority p to region R and stores it in the new region function  (Line 2). The new current priority
(Line 2). The new current priority  is, then, computed as the highest priority lower than p in
is, then, computed as the highest priority lower than p in  (Line 3). If, on the other hand, R is closed in
(Line 3). If, on the other hand, R is closed in  , a promotion merging R with some other \(\alpha \)-region contained in r is required. The next priority
, a promotion merging R with some other \(\alpha \)-region contained in r is required. The next priority  is set to the
is set to the  of R for player
of R for player  in the entire game
in the entire game  w.r.t. r (Line 4). Region R is, then, promoted to priority
w.r.t. r (Line 4). Region R is, then, promoted to priority  and all the priorities below
and all the priorities below  in the current region function r are reset (Line 5). The correctness of this last operation follows from Proposition 1.
in the current region function r are reset (Line 5). The correctness of this last operation follows from Proposition 1.
As already observed in Sect. 3, a dominion space, together with Algorithm 1, provides a sound and complete solution procedure. The following theorem states that the priority-promotion mechanism presented above is indeed a dominion space. The proof will be provided in the extended version of the paper.
Theorem 1
(Dominion Space). For a game  , the structure
, the structure  , where
, where  is given in Definition 4,
is given in Definition 4,  is the relation of Definition 5, and
is the relation of Definition 5, and  and
and  are the functions computed by Algorithms 2 and 3 is a dominion space.
are the functions computed by Algorithms 2 and 3 is a dominion space.
Complexity of PP Dominion Space. To conclude, we estimate the size and depth of dominion space  . This provides upper bounds on both the time and space needed by the search procedure
. This provides upper bounds on both the time and space needed by the search procedure  computing dominions. By looking at the definition of state space
computing dominions. By looking at the definition of state space  , it is immediate to see that, for a game
, it is immediate to see that, for a game  with n positions and k priorities, the number of states is bounded by \(k^{n}\). Indeed, there are at most \(k^{n}\) functions
with n positions and k priorities, the number of states is bounded by \(k^{n}\). Indeed, there are at most \(k^{n}\) functions  from positions to priorities that can be used as region function of a state. Note that the associated current priority is uniquely determined by the content of the region function. Measuring the depth is a little trickier. A coarse bound can be obtained by observing that there is an homomorphism from
from positions to priorities that can be used as region function of a state. Note that the associated current priority is uniquely determined by the content of the region function. Measuring the depth is a little trickier. A coarse bound can be obtained by observing that there is an homomorphism from  to the well-founded partial order, in which the region function r of a state is replaced by a partial function
to the well-founded partial order, in which the region function r of a state is replaced by a partial function  with the following properties: it assigns to each priority
with the following properties: it assigns to each priority  the size
the size  of the associated region
of the associated region  . The order
. The order  between two pairs is derived from the one on the states, by replacing
between two pairs is derived from the one on the states, by replacing  with
with  . This homomorphism ensures that every chain in
. This homomorphism ensures that every chain in  corresponds to a chain in the new partial order. Moreover, there are exactly
corresponds to a chain in the new partial order. Moreover, there are exactly  partial functions f such that
partial functions f such that  . Consequently, every chain cannot be longer than
. Consequently, every chain cannot be longer than  , where e is the Euler constant. By further exploiting the structure of the space, one can obtain a recurrence relation expressing a slightly better upper bound, whose explicit solution is
, where e is the Euler constant. By further exploiting the structure of the space, one can obtain a recurrence relation expressing a slightly better upper bound, whose explicit solution is  . Then, by applying a standard approximation via geometric series based on the inequality
. Then, by applying a standard approximation via geometric series based on the inequality  , we derive the asymptotic bound stated by the following theorem. A formal account of the recurrence relation will be provided in the extended version of this article.
, we derive the asymptotic bound stated by the following theorem. A formal account of the recurrence relation will be provided in the extended version of this article.
Theorem 2
(Size & Depth Upper Bounds). The size of a PP dominion space \(\mathcal {R}\) with  positions and \(k \in [1, n]\) priorities is bounded by \(k^{n}\). Moreover, if \(2 \le k\), its depth is bounded by
positions and \(k \in [1, n]\) priorities is bounded by \(k^{n}\). Moreover, if \(2 \le k\), its depth is bounded by  , which is less than \(3 \frac{n - k + 1}{n - 2k + 3} \left( \!{\texttt {e}} \frac{n - 2}{k - 2} \right) ^{k - 2}\), if
, which is less than \(3 \frac{n - k + 1}{n - 2k + 3} \left( \!{\texttt {e}} \frac{n - 2}{k - 2} \right) ^{k - 2}\), if  , and less than \(3(2^{n - 2} - c (\frac{n - 2}{k - 2})^{k - 2})\), for a constant \(c \>0\), otherwise.
, and less than \(3(2^{n - 2} - c (\frac{n - 2}{k - 2})^{k - 2})\), for a constant \(c \>0\), otherwise.
Unfortunately, due to the reset operations performed after each promotion, an exponential worst-case can actually be built. Indeed, consider the game  having all positions ruled by player 0 and containing h chains of length \(2m + 1\) that converge into a single position of priority 0 with a self loop. The i-th chain has a head of priority \(4k - i\) and a body composed of m blocks of two positions having priority \(2i - 1\) and 2i, respectively. The first position in each block also has a self loop. An instance of this game with \(m = 2\) and \(h = 4\) is depicted in Fig. 2. The labels of the positions correspond to the associated priorities and the highlighted area at the bottom of the figure groups together the last blocks of the chains. Intuitively, the execution depth of the PP dominion space for this game is exponential, since the consecutive promotion operations performed on each chain can simulate the increments of a counter up to m. Also, the priorities are chosen in such a way that, when the i-th counter is incremented, all the j-th counters with
having all positions ruled by player 0 and containing h chains of length \(2m + 1\) that converge into a single position of priority 0 with a self loop. The i-th chain has a head of priority \(4k - i\) and a body composed of m blocks of two positions having priority \(2i - 1\) and 2i, respectively. The first position in each block also has a self loop. An instance of this game with \(m = 2\) and \(h = 4\) is depicted in Fig. 2. The labels of the positions correspond to the associated priorities and the highlighted area at the bottom of the figure groups together the last blocks of the chains. Intuitively, the execution depth of the PP dominion space for this game is exponential, since the consecutive promotion operations performed on each chain can simulate the increments of a counter up to m. Also, the priorities are chosen in such a way that, when the i-th counter is incremented, all the j-th counters with  are reset. Therefore, the whole game simulates a counter with h digits taking values from 0 to m. Hence, the overall number of performed promotions is \((m + 1)^{h}\). The search procedure on
are reset. Therefore, the whole game simulates a counter with h digits taking values from 0 to m. Hence, the overall number of performed promotions is \((m + 1)^{h}\). The search procedure on  starts by building the four open 1-regions \(\{ 15 \}\), \(\{ 13 \}\), \(\{ 11 \}\), and \(\{ 9 \}\) and the open 0-region \(\{ 8', 7'', 8'' \}\), where we use apices to distinguish different positions with the same priority. This state represents the configuration of the counter, where all four digits are set to 0. The closed 1-region \(\{ 7' \}\) is then found and promoted to 9. Consequently, the previously computed 0-region with priority 8 is reset and the new region is maximised to obtain the open 1-region \(\{ 9, 7', 8' \}\). Now, the counter is set to 0001.
starts by building the four open 1-regions \(\{ 15 \}\), \(\{ 13 \}\), \(\{ 11 \}\), and \(\{ 9 \}\) and the open 0-region \(\{ 8', 7'', 8'' \}\), where we use apices to distinguish different positions with the same priority. This state represents the configuration of the counter, where all four digits are set to 0. The closed 1-region \(\{ 7' \}\) is then found and promoted to 9. Consequently, the previously computed 0-region with priority 8 is reset and the new region is maximised to obtain the open 1-region \(\{ 9, 7', 8' \}\). Now, the counter is set to 0001.
After that, the open 0-region \(\{ 8'' \}\) and the closed 1-region \(\{ 7'' \}\) are computed. The latter one is promoted to 9 and maximised to attract position \(8''\). This completes the 1-region containing the entire chain ending in 9. The value of the counter is now 0002. At this point, immediately after the construction of the open 0-region \(\{ 6', 5'', 6'' \}\), the closed 1-region \(\{ 5' \}\) is found, promoted to 11, and maximised to absorb position \(6'\). Due to the promotion, the positions in the 1-region with priority 9 are reset to their original priority and all the work done to build it gets lost. This last operation represents the reset of the least significant digit of the counter, caused by the increment of the second one, i.e., the counter displays 0010. Following similar steps, the process carries on until each chain is grouped in a single region. The corresponding state represents the configuration of the counter in which all digits are set to m. Thus, after an exponential number promotions, the closed 0-region \(\{ 0 \}\) is eventually obtained as solution.
Theorem 3
(Execution-Depth Lower Bounds). For all numbers \(h \in \mathbb {N}\), there exists a PP dominion space \(\mathcal {R}_h\) with \(k = 2h + 1\) positions and priorities, whose execution depth is \(3 \cdot 2^{h} - 2 = \Theta {2^{k / 2}}\). Moreover, for all numbers \(m \in \mathbb {N}_{+}\), there exists a PP dominion space \(\mathcal {R}_{m,h}\) with \(n = (2m + 1) \cdot h + 1\) positions and \(k = 3h + 1\) priorities, whose execution depth is  .
.
Observe that, in the above theorem, we provide two different exponential lower bounds. The general one, with k / 3 as exponent and a parametric base, is the result of the game  described in the previous paragraph, where \(k = 3h + 1\). The other bound, instead, has a base fixed to 2, but the worse exponent k / 2. We conjecture that the given upper bound could be improved to match the exponent k / 2 of this lower bound. In this way, we would obtain an algorithm with an asymptotic behaviour comparable with the one exhibited by the small-progress measure procedure [32]. This study will be further pursued in the extended version of the article.
described in the previous paragraph, where \(k = 3h + 1\). The other bound, instead, has a base fixed to 2, but the worse exponent k / 2. We conjecture that the given upper bound could be improved to match the exponent k / 2 of this lower bound. In this way, we would obtain an algorithm with an asymptotic behaviour comparable with the one exhibited by the small-progress measure procedure [32]. This study will be further pursued in the extended version of the article.
5 Experimental Evaluation
In order to assess the effectiveness of the proposed approach, the new technique described above has been implemented in the tool PGSolver [28], which collects implementations of several parity game solvers proposed in the literature. This software framework, implemented in OCaml, also provides a benchmarking tool, which can generate different forms of parity games. The available benchmarks divide into concrete problems and synthetic ones. The concrete benchmarks encode validity and verification problems for temporal logics. They consist in parity games resulting from encodings of the language inclusion problem between automata, specifically a non-deterministic Büchi automaton and a deterministic one, reachability problems, namely the Tower of Hanoi problem, and fairness verification problems, the Elevator problem (see [28]). The synthetic benchmarks divide into randomly generated games and various families corresponding to difficult cases (clique and ladder-like games) and worst cases of the solvers implemented in PGSolver. To fairly compare the different solution techniques used by the underlying algorithms, the solvers involved in the experiments have been isolated from the generic solver implemented in PGSolver, which exploits game transformation and decomposition techniques in the attempt to speed up the solution process. However, those optimisations can, in some cases, solve the game without even calling the selected algorithm, and, in other cases, the resulting overhead can even outweigh the solver time, making the comparison among solvers virtually worthless [28]. Experiments were also conducted with different optimisations enabled and the results exhibit the same pattern emerging in the following experimental evaluation.
The algorithms considered in the experimentation are the Zielonka algorithm Rec [54], its two dominion decomposition variants, Dom [33, 34] and Big [48], the strategy improvement algorithm Str [52], and the one proposed in this article, PP. Small progress measure [32] is not included, since it could not solve any of the tested benchmarks within the available computational resourcesFootnote 1.
Special Families. Table 2 displays the results of all the solvers involved on the benchmark families available in PGSolver. We only report on the biggest instances we could deal with, given the available computational resourcesFootnote 2. The parameter Size refers to the number of positions in the games and the best performance are emphasised in bold. The first three rows consider the concrete verification problems mentioned above. On the Tower of Hanoi problem all the solvers perform reasonably well, except for Str due its high memory requirements. The Elevator problem proved to be very demanding in terms of memory for all the solvers, except for our new algorithm and Dom, which, however, could not solve it within the time limit of 10 min. Our solver performs extremely well on both this benchmark and on Language Inclusion, which could be solved only by Rec among the other solvers. On the worst case benchmarks, it performs quite well also on Ladder, Strategy Improvement, and Clique, which proved to be considerably difficult for all the other solvers. It was outperformed only on the last three ones: the Modelchecker, the Recursive Ladder, and Jurdziński games. Despite this fact, the new solver exhibit the most consistent behaviour overall on these benchmarks. Indeed, in all those benchmarks, the priority promotion algorithm requires no promotions regardless of the input parameters, except for the elevator problem, where it performs only two promotions.
Random Games. Figure 3 compares the running times (left-hand side) and memory requirements (right-end side) of the new algorithm PP against Rec and Str on 2000 random games of size ranging from 5000 to 20000 positions and 2 outgoing moves per position. Interestingly, these random games proved to be quite challenging for all the considered solvers. We set a time-out to 180 s (3 min). Both Dom and Big perform quite poorly on those games, hitting the time-out already for very small instances, and we decided to leave them out of the picture. The behaviour of the solvers is typically highly variable even on games of the same size and priorities. To summarise the results, the average running time on clusters of games seemed the most appropriate choice in this case. Therefore, each point in the graph shows the average time over a cluster of 100 different games of the same size: for each size value n, we chose a number \(k = n \cdot i / 10\) of priorities, with  , and 10 random games were generated for each pair of n and k. The new algorithm perform significantly better than the others on those games. The right-hand side graph also shows that the theoretical improvement on the auxiliary memory requirements of the new algorithm has a considerable practical impact on memory consumption compared to the other solvers. We also experimented on random games with a higher number of moves per position. The resulting games turn out to be much easier to solve for all the solvers. This behaviour might depend on the specific random generator provided by PGSolver. However, those experiments still show better performance by the new algorithm w.r.t. the competitor ones. Due to the space constraints, the corresponding results will be reported in the extended version of the paper.
, and 10 random games were generated for each pair of n and k. The new algorithm perform significantly better than the others on those games. The right-hand side graph also shows that the theoretical improvement on the auxiliary memory requirements of the new algorithm has a considerable practical impact on memory consumption compared to the other solvers. We also experimented on random games with a higher number of moves per position. The resulting games turn out to be much easier to solve for all the solvers. This behaviour might depend on the specific random generator provided by PGSolver. However, those experiments still show better performance by the new algorithm w.r.t. the competitor ones. Due to the space constraints, the corresponding results will be reported in the extended version of the paper.
6 Discussion
We considered the problem of solving Parity Games, a special form of infinite-duration games over graphs having relevant applications in various branches of Theoretical Computer Science. We proposed a novel solution technique, based on a priority-promotion mechanism. Based on this approach, a new solution algorithm have been presented and studied. We gave proofs of its correctness and provided an accurate analysis of its time and space complexities.
As far as time complexity is concerned, an exponential upper bound in the number of priorities has been given. A lower bound for the worst-case was also presented in the form of a family of parity games on which the new technique exhibits an exponential behaviour. On the bright side, the new solution exhibits the best space complexity among the currently known algorithms for parity games. In fact, we showed that the maximal additional space needed to solve a parity game is linear in the number of positions, logarithmic in the number of priorities, and independent from the number of moves in the game. This is an important result, in particular considering that in practical applications we often need to deal with games having a very high number of positions, moves, and, in some cases, priorities. Therefore, low space requirements are essential for practical scalability.
To assess the effectiveness of the new approach, experiments were carried out against concrete and synthetic problems. We compared the new algorithm with the state-of-the-art solvers implemented in PGSolver. The results are very promising, showing that the proposed approach is extremely effective in practice, often substantially better than existing ones. This suggests that the new approach is worth pursuing further. Therefore, we are currently investigating new and clever priority-promotion policies that try to minimise the number of region resets after a priority promotion.
It would be interesting to investigate the applicability of the priority promotion approach to related problems, such as prompt-parity games [42] and similar conditions [12, 26, 27], and even in wider contexts like mean-payoff games [13, 16] and energy games [10, 11].
Notes
- 1.
Experiments were carried out on a 64-bit 3.1 GHz Intel® quad-core machine, with i5-2400 processor and 8 GB of RAM, running Ubuntu 12.04 with Linux kernel version 3.2.0. PGSolver was compiled with OCaml version 2.12.1.
- 2.
The instances were generated with the following PGSolver commands: towersofhanoi 13, elevatorgame 8, langincl 500 100, laddergame 4000000, stratimprgen -pg friedmannsubexp 1000, modelcheckerladder 2500000, clique game 8000, recursiveladder 10000, and jurdzinskigame 100 100.
References
Agrawal, M., Kayal, N., Saxena, N.: PRIMES is in P. Ann. Math. 160(2), 781–793 (2004)
Alur, R., Henzinger, T., Kupferman, O.: Alternating-time temporal logic. JACM 49(5), 672–713 (2002)
Apt, K., Grädel, E.: Lectures in Game Theory for Computer Scientists. Cambridge University Press, Cambridge (2011)
Benerecetti, M., Mogavero, F., Murano, A.: Substructure temporal logic. In: LICS 2013, pp. 368–377. IEEE Computer Society (2013)
Benerecetti, M., Mogavero, F., Murano, A.: Reasoning about substructures and games. TOCL 16(3), 25:1–25:46 (2015)
Berwanger, D., Dawar, A., Hunter, P., Kreutzer, S.: DAG-width and parity games. In: Durand, B., Thomas, W. (eds.) STACS 2006. LNCS, vol. 3884, pp. 524–536. Springer, Heidelberg (2006)
Berwanger, D., Grädel, E.: Games and model checking for guarded logics. In: Nieuwenhuis, R., Voronkov, A. (eds.) LPAR 2001. LNCS (LNAI), vol. 2250, pp. 70–84. Springer, Heidelberg (2001)
Berwanger, D., Grädel, E.: Fixed-point logics and solitaire games. TCS 37(6), 675–694 (2004)
Berwanger, D., Grädel, E., Kaiser, L., Rabinovich, R.: Entanglement and the complexity of directed graphs. TCS 463, 2–25 (2012)
Chatterjee, K., Doyen, L.: Energy parity games. TCS 458, 49–60 (2012)
Chatterjee, K., Doyen, L., Henzinger, T., Raskin, J.-F.: Generalized mean-payoff and energy games. In: FSTTCS 2010. LIPIcs, vol. 8, pp. 505–516. Leibniz-Zentrum fuer Informatik (2010)
Chatterjee, K., Henzinger, T., Horn, F.: Finitary winning in omega-regular games. TOCL 11(1), 1:1–1:26 (2010)
Chatterjee, K., Henzinger, T., Jurdziński, M.: Mean-payoff parity games. In: LICS 2005, pp. 178–187. IEEE Computer Society (2005)
Chatterjee, K., Henzinger, T., Piterman, N.: Strategy Logic. IC 208(6), 677–693 (2010)
Condon, A.: The complexity of stochastic games. IC 96(2), 203–224 (1992)
Ehrenfeucht, A., Mycielski, J.: Positional strategies for mean payoff games. IJGT 8(2), 109–113 (1979)
Emerson, E., Jutla, C.: Tree automata, mucalculus, and determinacy. In: FOCS 1991, pp. 368–377. IEEE Computer Society (1991)
Emerson, E.A., Jutla, C.S., Sistla, A.P.: On model-checking for fragments of \(\mu \)-calculus. In: Courcoubetis, C. (ed.) CAV 1993. LNCS, vol. 697, pp. 385–396. Springer, Heidelberg (1993)
Emerson, E., Jutla, C., Sistla, A.: On model checking for the mucalculus and its fragments. TCS 258(1–2), 491–522 (2001)
Emerson, E., Lei, C.-L.: Temporal reasoning under generalized fairness constraints. In: Monien, B., Vidal-Naquet, G. (eds.) STACS 1986. LNCS, vol. 210, pp. 267–278. Springer, Heidelberg (1986)
Fearnley, J.: Non-oblivious strategy improvement. In: Clarke, E.M., Voronkov, A. (eds.) LPAR-16 2010. LNCS, vol. 6355, pp. 212–230. Springer, Heidelberg (2010)
Fearnley, J., Lachish, O.: Parity games on graphs with medium tree-width. In: Murlak, F., Sankowski, P. (eds.) MFCS 2011. LNCS, vol. 6907, pp. 303–314. Springer, Heidelberg (2011)
Fearnley, J., Schewe, S.: Time and parallelizability results for parity games with bounded treewidth. In: Czumaj, A., Mehlhorn, K., Pitts, A., Wattenhofer, R. (eds.) ICALP 2012, Part II. LNCS, vol. 7392, pp. 189–200. Springer, Heidelberg (2012)
Fellows, M., Koblitz, N.: Self-witnessing polynomial-time complexity and prime factorization. In: CSCT 1992, pp. 107–110. IEEE Computer Society (1992)
Fellows, M., Koblitz, N.: Self-witnessing polynomial-time complexity and prime factorization. DCC 2(3), 231–235 (1992)
Fijalkow, N., Zimmermann, M.: Cost-parity and cost-streett games. In: FSTTCS 2012. LIPIcs, vol. 18, pp. 124–135. Leibniz-Zentrum fuer Informatik (2012)
Fijalkow, N., Zimmermann, M.: Cost-parity and cost-streett games. LMCS 10(2), 1–29 (2014)
Friedmann, O., Lange, M.: Solving parity games in practice. In: Liu, Z., Ravn, A.P. (eds.) ATVA 2009. LNCS, vol. 5799, pp. 182–196. Springer, Heidelberg (2009)
Grädel, E., Thomas, W., Wilke, T. (eds.): Automata, Logics, and Infinite Games: A Guide to Current Research. LNCS, vol. 2500. Springer, Heidelberg (2002)
Gurvich, V., Karzanov, A., Khachivan, L.: Cyclic games and an algorithm to find minimax cycle means in directed graphs. USSRCMMP 28(5), 85–91 (1990)
Jurdziński, M.: Deciding the winner in parity games is in UP \(\cap \) co-Up. IPL 68(3), 119–124 (1998)
Jurdziński, M.: Small progress measures for solving parity games. In: Reichel, H., Tison, S. (eds.) STACS 2000. LNCS, vol. 1770, pp. 290–301. Springer, Heidelberg (2000)
Jurdziński, M., Paterson, M., Zwick, U.: A deterministic subexponential algorithm for solving parity games. In: SODA 2006, pp. 117–123. Society for Industrial and Applied Mathematics (2006)
Jurdziński, M., Paterson, M., Zwick, U.: A deterministic subexponential algorithm for solving parity games. SJM 38(4), 1519–1532 (2008)
Klarlund, N., Kozen, D.: Rabin measures and their applications to fairness and automata theory. In: LICS 1991, pp. 256–265. IEEE Computer Society (1991)
Kupferman, O., Vardi, M.: Weak alternating automata and tree automata emptiness. In: STOC 1998, pp. 224–233. Association for Computing Machinery (1998)
Martin, A.: Borel determinacy. Ann. Math. 102(2), 363–371 (1975)
Martin, A.: A purely inductive proof of borel determinacy. In: SPM 1982. Recursion Theory, pp. 303–308. American Mathematical Society and Association for Symbolic Logic (1985)
McNaughton, R.: Infinite games played on finite graphs. APAL 65, 149–184 (1993)
Mogavero, F., Murano, A., Perelli, G., Vardi, M.Y.: What makes Atl* decidable? a decidable fragment of strategy logic. In: Koutny, M., Ulidowski, I. (eds.) CONCUR 2012. LNCS, vol. 7454, pp. 193–208. Springer, Heidelberg (2012)
Mogavero, F., Murano, A., Perelli, G., Vardi, M.: Reasoning about strategies: on the model-checking problem. TOCL 15(4), 34:1–34:42 (2014)
Mogavero, F., Murano, A., Sorrentino, L.: On promptness in parity games. In: McMillan, K., Middeldorp, A., Voronkov, A. (eds.) LPAR-19 2013. LNCS, vol. 8312, pp. 601–618. Springer, Heidelberg (2013)
Mogavero, F., Murano, A., Vardi, M.: Reasoning About Strategies. In: FSTTCS 2010. LIPIcs, vol. 8, pp. 133–144. Leibniz-Zentrum fuer Informatik (2010)
Mostowski, A.: Regular expressions for infinite trees and a standard form of automata. In: Skowron, A. (ed.) SCT 1984. LNCS, vol. 208, pp. 157–168. Springer, Heidelberg (1984)
Mostowski, A.: Games with Forbidden Positions. University of Gdańsk, Gdańsk, Poland, Technical report (1991)
Obdržálek, J.: Fast mu-calculus model checking when tree-width is bounded. In: Hunt Jr., W.A., Somenzi, F. (eds.) CAV 2003. LNCS, vol. 2725, pp. 80–92. Springer, Heidelberg (2003)
Obdržálek, J.: Clique-width and parity games. In: Duparc, J., Henzinger, T.A. (eds.) CSL 2007. LNCS, vol. 4646, pp. 54–68. Springer, Heidelberg (2007)
Schewe, S.: Solving parity games in big steps. In: Arvind, V., Prasad, S. (eds.) FSTTCS 2007. LNCS, vol. 4855, pp. 449–460. Springer, Heidelberg (2007)
Schewe, S.: An optimal strategy improvement algorithm for solving parity and payoff games. In: Kaminski, M., Martini, S. (eds.) CSL 2008. LNCS, vol. 5213, pp. 369–384. Springer, Heidelberg (2008)
Schewe, S.: ATL* satisfiability is 2EXPTIME-complete. In: Aceto, L., Damgård, I., Goldberg, L.A., Halldórsson, M.M., Ingólfsdóttir, A., Walukiewicz, I. (eds.) ICALP 2008, Part II. LNCS, vol. 5126, pp. 373–385. Springer, Heidelberg (2008)
Schewe, S., Finkbeiner, B.: Satisfiability and finite model property for the alternating-Time \(\mu \)-calculus. In: Ésik, Z. (ed.) CSL 2006. LNCS, vol. 4207, pp. 591–605. Springer, Heidelberg (2006)
Vöge, J., Jurdziński, M.: A discrete strategy improvement algorithm for solving parity games. In: Emerson, E.A., Sistla, A.P. (eds.) CAV 2000. LNCS, vol. 1855, pp. 202–215. Springer, Heidelberg (2000)
Wilke, T.: Alternating tree automata, parity games, and modal mu calculus. BBMS 8(2), 359–391 (2001)
Zielonka, W.: Infinite games on finitely coloured graphs with applications to automata on infinite trees. TCS 200(1–2), 135–183 (1998)
Zwick, U., Paterson, M.: The complexity of mean payoff games on graphs. TCS 158(1–2), 343–359 (1996)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this paper
Cite this paper
Benerecetti, M., Dell’Erba, D., Mogavero, F. (2016). Solving Parity Games via Priority Promotion. In: Chaudhuri, S., Farzan, A. (eds) Computer Aided Verification. CAV 2016. Lecture Notes in Computer Science(), vol 9780. Springer, Cham. https://doi.org/10.1007/978-3-319-41540-6_15
Download citation
DOI: https://doi.org/10.1007/978-3-319-41540-6_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-41539-0
Online ISBN: 978-3-319-41540-6
eBook Packages: Computer ScienceComputer Science (R0)





 is the set of all pairs
is the set of all pairs  , called states, composed of a region function
, called states, composed of a region function  and a priority
and a priority  such that (a)
such that (a)  , and (c)
, and (c) 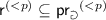 ;
; ;
; , it holds that
, it holds that 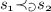 iff either (a) there exists a priority
iff either (a) there exists a priority  with
with  such that (a.i)
such that (a.i) 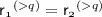 and (a.ii)
and (a.ii) 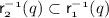 , or (b) both (b.i)
, or (b) both (b.i)  and (b.ii)
and (b.ii)  hold.
hold.
 game.
game.