Tridiagonalization of a Symmetric Band Matrix

Abstract

The well known method proposed by Givens [1] reduces a full symmetric matrix A = (a _ik ) of order n by a sequence of appropriately chosen elementary orthogonal transformations (in the following called Jacobi rotations) to triput diagonal form. This is achieved by (n - 1)(n - 2)/2 Jacobi rotations, each of which annihilates one of the elements a _ik with |i - k|>1. If this process is applied in one of its usual ways to a symmetric band matrix A = (a _ik ) of order n and with the band width m>1, i.e. with

$${a_{ik}} = 0{\rm{ for all }}i{\rm{ and }}k{\rm{ with |}}i - k{\rm{| >}}m,$$

((1))

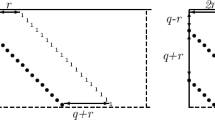
it would of course produce a tridiagonal matrix, too. But the rotations generate immediately nonvanishing elements outside the original band that show the tendency to fill out the matrix. Thus it seems that little profit with respect to computational and storage requirements may be taken from the property of the given matrix A to be of band type.

Prepublished in Numer. Math. 12, 231–241 (1968).