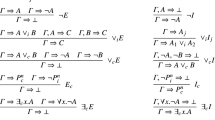Sequent-systems and groupoid models. II

Abstract

The purpose of this paper is to connect the proof theory and the model theory of a family of prepositional logics weaker than Heyting's. This family includes systems analogous to the Lambek calculus of syntactic categories, systems of relevant logic, systems related to BCK algebras, and, finally, Johansson's and Heyting's logic. First, sequent-systems are given for these logics, and cut-elimination results are proved. In these sequent-systems the rules for the logical operations are never changed: all changes are made in the structural rules. Next, Hilbert-style formulations are given for these logics, and algebraic completeness results are demonstrated with respect to residuated lattice-ordered groupoids. Finally, model structures related to relevant model structures (of Urquhart, Fine, Routley, Meyer, and Maksimova) are given for our logics. These model structures are based on groupoids parallel to the sequent-systems. This paper lays the ground for a kind of correspondence theory for axioms of logics with implication weaker than Heyting's, a correspondence theory analogous to the correspondence theory for modal axioms of normal modal logics.

Below is the sequel to the first part of the paper, which appeared in the previous issue of this journal (vol. 47 (1988), pp. 353–386). The first part contained sections on sequent-systems and Hilbert-formulations, and here is the third section on groupoid models. This second part is meant to be read in conjunction with the first part.