1 Introduction

The theoretical and experimental studies of the magnetic materials with large magnetocaloric effect (MCE) have been the interest of many researchers thanks to their great potential applications in energy-efficient magnetic refrigeration (MR) technology [1,2,3]. Concerning the first reason, it pertains to the fact that magnetic cooling offers a competitive alternative to conventional gas compression-expansion refrigeration systems since it is highly energy-efficient and environment friendly. Actually, the need is neither for ozone-depleting nor global warming volatile refrigerants. As for the second one, it relates to the fact that magnetic refrigeration close to room temperature is only possible with materials that undergo a phase transition close to the working temperature of a refrigerator. Hence, the characterization of magnetocaloric materials commonly tends to become linked to a comprehensive study of their phase transition, which is also important from a fundamental standpoint. Many magnetocaloric materials have been thoroughly investigated over the past years due to their possible application in magnetic refrigeration near room temperature region, e.g., Gd5Si2Ge2 alloy [4], NiMnGa [5], MnFeP1−x As x [6], LaFe13−x Si x [7], and ferromagnetic perovskite manganites [8,9,10]. Perovskite-like manganites La1−x Ca x MnO3 exhibit a variety of physical properties depending on the Ca concentration x. The strong correlation among magnetic, electronic, orbital, and transport properties of manganites makes these systems principally sensitive to external perturbations, such as temperature variation, magnetic field application, or high pressure [11, 12].

The present research is a theoretical work that undertakes the study of the effect of quenching on the correlation between the electrical and magnetic properties of the La0.8Ca0.2MnO3 polycrystalline.

2 Theoretical Considerations

Using the phenomenological model, described in [13, 14], the variation of the magnetization with temperature is simulated by:

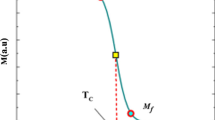
$$\begin{array}{@{}rcl@{}} M(T,H=H_{\max} )&=&(\frac{M_{i} -M_{f}} {2})\\&&\times \left[ {\tanh (A(T_{C} -T))} \right]+BT+C \end{array} $$
(1)

where M i is an initial value of magnetization at ferromagnetic-paramagnetic transition and is the point of magnetization just after the linear line of magnetization (FM) and before the curvature (PM), while M f is a final value of magnetization at paramagnetic-ferromagnetic transition exactly the point just after the curvature and before the linear line of magnetization (Fig. 1); \(A=\frac {2(B-S_{\mathrm {C}})}{M_{i} -M_{\mathrm {f}}}\); B is the magnetization sensitivity \(\frac {dM}{dT}\) at ferromagnetic state before transition; S C is the magnetization sensitivity \(\frac {dM}{dT}\) at Curie temperature T C; and \(C=\left ({\frac {M_{i} -M_{\mathrm {f}}} {2}} \right )-BT_{\mathrm {C}}\).

Fig. 1
figure 1

Temperature dependence of magnetization in constant applied magnetic field

Full size image

The magnetic entropy change of a magnetic system under adiabatic magnetic field variation from 0 to final value H max is available by:

$$ {\Delta} S_{\mathrm{M}} \,=\,\left( -A\left( {\frac{M_{i} -M_{\mathrm{f}}} {2}} \right)\sec{} h^{2}\left.(A(T_{\mathrm{C}} -T))+B\right)H_{\max} \right) $$
(2)

where sec h(x) = 1 / cos h(x).

The foundation of large magnetic entropy change is attributed to high magnetic moment and rapid change of magnetization at T C. A result of (2) is a maximum magnetic entropy change ΔS max (where T = T C), which can be evaluated as the following equation:

$$ {\Delta} S_{\max} =\left( {-A\left( {\frac{M_{i} -M_{\mathrm{f}}} {2}} \right)+B} \right)H_{\max} $$
(3)

Equation 3 is important for taking into consideration the value of the magnetic entropy change to evaluate magnetic cooling efficiency with its full-width at half-maximum.

The determination of full-width at half-maximum δ T FWHM can be carried out as follows:

$$ \delta_{\text{FWHM}} =\frac{2}{A}\sec {}h\left[ {\sqrt {\frac{2A(M_{i} -M_{\mathrm{f}} )}{A(M_{i} -M_{\mathrm{f}} )+2B}}} \right] $$
(4)

The magnetic cooling efficiency is estimated by considering the magnitude of magnetic entropy change ΔS M, and its full-width at half-maximum δ T FWHM [15] The product of − ΔS M and δ T FWHM is called relative cooling power (RCP) based on magnetic entropy change:

$$\begin{array}{@{}rcl@{}} \text{RCP}&=&-{\Delta} S_{\mathrm{M}} (T,H_{\max} )\times \delta_{\text{FWHM}}\\ &=&\left( {M_{i} -M_{\mathrm{f}} -2\frac{B}{A}} \right)H_{\max}\\ &&\times \sec {} h\left[ {\sqrt {\frac{2A(M_{i} -M_{\mathrm{f}} )}{A(M_{i} -M_{\mathrm{f}} )+2B}}} \right] \end{array} $$
(5)

The magnetization-related change of the specific heat is given by [16]:

$$ {\Delta} C_{\text{P,H}} =T\frac{\delta {\Delta} S_{\mathrm{M}}} {\delta T} $$
(6)

According to this model, ΔC P,Hcan be rewritten as:

$$\begin{array}{@{}rcl@{}} {\Delta} C_{\text{P,H}} &=&-TA^{2}(M_{i} -M_{\mathrm{f}} )\sec h^{2}\left[ {A\left( {T_{\mathrm{C}} -T} \right)} \right]\\&&\times \tanh \left[ {A\left( {T_{\mathrm{C}} -T} \right)} \right]H_{\max} \end{array} $$
(7)

On the other hand, the magnetic entropy change (ΔS M) can be estimated using the following equation [17]:

$$ {\Delta} S= - \alpha {\int\limits_{0}^{H}} {\left[ {\frac{\delta \text{Ln}\left( \rho \right)}{\delta T}} \right]}_{H} dH $$
(8)

where the parameter α determines the magnetic properties of the sample. Different functional dependences between M and ρ have been used to estimate α directly where \(\rho = \rho _{0} \exp \left ({\frac {-M}{\alpha }}\right )\) [17]. O’Donnell et al. [18] pointed out that the exact equation should be \(\rho =\text { } \rho _{0} \exp \left ({\frac {-M^{2}}{\alpha }} \right )\), while Chen et al. [19] proposed the equation \(\rho = \rho _{0} \exp \left ({\frac {-M^{2}}{\alpha T}} \right )\) for small and intermediate magnetization near and above the Curie temperature.

3 Model Application and Discussion

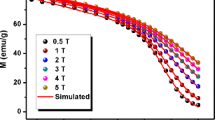
In order to apply the phenomenological model, Fig. 2 presents the magnetization versus temperature in different applied magnetic fields. This figure displays the simulated (solid line) and experimental results for La0.8Ca0.2MnO3 sample. It can be seen that the computational results are in a good agreement with the experimental results.

Fig. 2
figure 2

Magnetization in different applied magnetic fields for the La0.8Ca0.2MnO3 sample versus temperature. Symbols are the experimental results and solid lines are the graphs fitted by (1)

Full size image

The best-fit parameters are given in Table 1.

Table 1 Model parameters for La0.8Ca0.2MnO3 in different applied magnetic fields
Full size table

What is worthy to note is that the Curie temperature T C increases significantly with the increase in magnetic field and the magnetization exhibits a continuous change around T C in different magnetic fields.

We have recently studied the magnetocaloric effect of La0.8Ca0.2MnO3 sample [9] using the measured magnetization versus the applied magnetic field M(H, T) at different temperatures (T) around T C. In order to check the validity of this model, the experimental results from the magnetic entropy change have been fitted by (3) (Fig. 3). It is seen that the calculation results are in accordance with the experimental ones. Although the magnetocaloric effect increases with the increase of the applied magnetic fields, the maxima observed in the ΔS M curves are related to a spin reorientation that occurs continuously. This can be explained by the fact that the effect reaches its maximum in the vicinity of magnetic phase transition points.

Fig. 3
figure 3

Magnetic entropy change as a function of temperature for La0.8Ca0.2MnO3 in different applied magnetic field variations. Symbols are the experimental results and solid lines are the graphs fitted by (2)

Full size image

Figure 4 shows the modeled results of specific heat versus temperature for La0.8Ca0.2MnO3 sample. The maximum and minimum values of specific heat change at different applied magnetic fields were calculated using (7) and listed in Table 2.

Fig. 4
figure 4

Heat capacity changes as function of temperature for La0.8Ca0.2MnO3 in different applied magnetic field variations. The inset shows the experimental and simulated results fitted by (7) to a field of 1 T

Full size image
Table 2 The predicted values of specific heat change in different applied magnetic fields
Full size table

From the ρ(H,T) curves plotted in Fig. 5, the magnetic entropy change (ΔS M) has been estimated using (8), for an applied magnetic field of 2 T. For this aim, and as shown in Fig. 6, the variation ρ versus M, M 2 and M 2/T was studied. This research work has proven that the resistivity strongly depends on M 2/T. The results on the calculation of the change in magnetic entropy by (8) and the Maxwell relation, described in our previous research work [9], are shown in Fig. 7, where the value of the parameter α for our system is equal to 153.60 (emu) 2 g −2 K. This is determined from the fitting of ρ versus M 2/T curve around the transition temperature T C with the equation \(\rho =\rho _{0} \exp \left ({\frac {-M^{2}}{\alpha T}}\right )\) (Fig. 5).

Fig. 5
figure 5

Temperature dependence of the resistivity under different applied magnetic fields rising from 0 to 5 T for La0.8Ca0.2MnO3 compound

Full size image
Fig. 6
figure 6

ρ versus M, M 2, and M 2/T under the field of 2 T. Solid line is a fit to the formula \(\rho = \rho _{0} \exp \left ({\frac {-M^{2}}{\alpha T}} \right )\)

Full size image
Fig. 7
figure 7

Temperature dependence of the magnetic-entropy change measured and calculated using (8) an applied magnetic field of 2 T for La0.8Ca0.2MnO3 sample

Full size image

Eventually, the comparison in Fig. 8 shows the magnetic entropy changes determined according to Eqs. 3 and 8 by the experimental values determined from the M(H, T).

Fig. 8
figure 8

Temperature dependence of the magnetic-entropy change measured and calculated using Eqs. 3 and 8 an applied magnetic field of 2 T for La0.8Ca0.2MnO3 sample

Full size image

From this figure, we note that the good quantitative agreement between calculated and experimental data from such analysis would be quite unexpected, but the fact of observing qualitative agreement between them reveals a strong correlation of electrical and magnetic properties in the manganites of La0.8Ca0.2MnO3 type near the phase transition temperature.

4 Conclusions

The phenomenological model can be considered as another indirect method that determines the change in magnetic entropy from the data of M(T,H) measurements in manganites. Moreover, from the temperature dependence of the resistivity measured at several applied magnetic field ρ(H,T), we have calculated the magnetic entropy change based on the following equation:\({\Delta } S = -\alpha {\int \limits _{0}^{H}} {\left [ {\frac {\delta \text {Ln}\left (\rho \right )}{\delta T}} \right ]}_{H} dH\). An agreement between the experimental and calculated magnetic entropy change has been found. Finally, it is important to note that all equations derived for the magnetic entropy calculation are valid for other doping concentration such as such as 0.00 ≤ x ≤ 0.20.