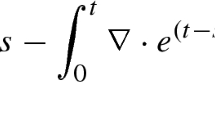Abstract
Consider a bounded domain\({{\Omega \subseteq \mathbb{R}^3}}\) with smooth boundary, some initial value \({{u_0 \in L^2_{\sigma}(\Omega )}}\), and a weak solution u of the Navier–Stokes system in \({{[0,T) \times\Omega,\,0 < T \le \infty}}\). Our aim is to develop regularity and uniqueness conditions for u which are based on the Besov space
with \({{2 < s < \infty,\,3 < q <\infty,\,\frac2{s}+\frac{3}{q} = 1}}\); here A denotes the Stokes operator. This space, introduced by Farwig et al. (Ann. Univ. Ferrara 55:89–110, 2009 and J. Math. Fluid Mech. 14: 529–540, 2012), is a subspace of the well known Besov space \({{{\mathbb{B}}^{-2/s}_{q,s}(\Omega )}}\), see Amann (Nonhomogeneous Navier–Stokes Equations with Integrable Low-Regularity Data. Int. Math. Ser. pp. 1–28. Kluwer/Plenum, New York, 2002). Our main results on the regularity of u exploits a variant of the space \({{B^{q,s}(\Omega )}}\) in which the integral in time has to be considered only on finite intervals (0, δ ) with \({{\delta \to 0}}\). Further we discuss several criteria for uniqueness and local right-hand regularity, in particular, if u satisfies Serrin’s limit condition \({{u\in L^{\infty}_{\text{loc}}([0,T);L^3_{\sigma}(\Omega ))}}\). Finally, we obtain a large class of regular weak solutions u defined by a smallness condition \({{\|u_0\|_{B^{q,s}(\Omega )} \le K}}\) with some constant \({{K=K(\Omega, q)>0}}\).
Similar content being viewed by others
References
Amann, H.: Nonhomogeneous Navier–Stokes Equations with Integrable Low-Regularity Data Int. Math. Ser. pp. 1–28. Kluwer/Plenum, New York (2002)
Farwig R., Kozono H., Sohr H.: Local in time regularity properties of the Navier–Stokes equations. Indiana Univ. Math. J. 56, 2111–2131 (2007)
Farwig R., Sohr H., Varnhorn W.: On optimal initial value conditions for local strong solutions of the Navier–Stokes equations. Ann. Univ. Ferrara 55, 89–110 (2009)
Farwig R., Sohr H., Varnhorn W.: Extensions of Serrin’s uniqueness and regularity conditions for the Navier–Stokes equations. J. Math. Fluid Mech. 14, 529–540 (2012)
Galdi, G.P.: An Introduction to the Mathematical Theory of the Navier–Stokes Equations, vol. I. Springer, New York (1994)
Giga Y.: Analyticity of the semigroup generated by the Stokes operator in L r spaces. Math. Z. 178, 297–329 (1981)
Giga Y.: Solutions for semilinear parabolic equations in Lp and regularity of weak solutions of the Navier–Stokes system. J. Differ. Equ. 61, 186–212 (1986)
Giga Y., Sohr H.: Abstract L q-estimates for the Cauchy problem with applications to the Navier–Stokes equations in exterior domains. J. Funct. Anal. 102, 72–94 (1991)
Kozono H.: Uniqueness and regularity of weak solutions to the Navier–Stokes equations. Lecture Notes in Num. Appl. Anal. Kinokuniya, Tokyo, 16, 161–208 (1998)
Kozono H., Sohr H.: Remark on uniqueness of weak solutions to the Navier–Stokes equations. Analysis 16, 255–271 (1996)
Mikhailov, A.S., Shilkin, T.N.: L 3,∞-solutions to the 3D-Navier–Stokes system in a domain with a curved boundary. Zap. Nauchn. Semin. POMI 336, 133–152 (2006) Russian. J. Math. Sci. 143 (2007) (English)
Seregin G.: On smoothness of L 3,∞-solutions to the Navier–Stokes equations up to boundary. Math. Ann. 332, 219–238 (2005)
Serrin, J.: The initial value problem for the Navier–Stokes equations. Nonlinear Problems. Proc. Sympos. Madison, pp. 69–98 (1963)
Sohr H.: The Navier–Stokes Equations. Birkhäuser Verlag, Basel (2001)
Sohr H.: A regularity class for the Navier–Stokes equations in Lorentz spaces. J. Evol. Equ. 1, 441–467 (2001)
Temam R.: Navier–Stokes Equations. North Holland, Amsterdam (1977)
Triebel H.: Interpolation Theory, Function Spaces, Differential Operators. North-Holland, Amsterdam (1978)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Farwig, R., Sohr, H. & Varnhorn, W. Besov Space Regularity Conditions for Weak Solutions of the Navier–Stokes Equations. J. Math. Fluid Mech. 16, 307–320 (2014). https://doi.org/10.1007/s00021-013-0154-1
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00021-013-0154-1