Adaptive Polynomial Filtering using Generalized Variable Step-Size Least Mean pth Power (LMP) Algorithm

Abstract

This correspondence presents the adaptive polynomial filtering using the generalized variable step-size least mean $p$th power (GVSS-LMP) algorithm for the nonlinear Volterra system identification, under the $\alpha$-stable impulsive noise environment. Due to the lack of finite second-order statistics of the impulse noise, we espouse the minimum error dispersion criterion as an appropriate metric for the estimation error, instead of the conventional minimum mean square error criterion. For the convergence of LMP algorithm, the adaptive weights are updated by adjusting $p\ge 1$ in the presence of impulsive noise characterized by $1<\alpha <2$. In many practical applications, the autocorrelation matrix of input signal has the larger eigenvalue spread in the case of nonlinear Volterra filter than in the case of linear finite impulse response filter. In such cases, the time-varying step-size is an appropriate option to mitigate the adverse effects of eigenvalue spread on the convergence of LMP adaptive algorithm. In this paper, the GVSS updating criterion is proposed in combination with the LMP algorithm, to identify the slowly time-varying Volterra kernels, under the non-Gaussian $\alpha$-stable impulsive noise scenario. The simulation results are presented to demonstrate that the proposed GVSS-LMP algorithm is more robust to the impulsive noise in comparison to the conventional techniques, when the input signal is correlated or uncorrelated Gaussian sequence, while keeping $1<p<\alpha <2$. It also exhibits flexible design to tackle the slowly time-varying nonlinear system identification problem.

Appendix

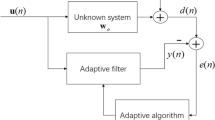
The literature [8, 30] of fixed step-size LMS (FSS-LMS) algorithm reflects a tradeoff between the misadjustment and speed of adaptation, which depicts that a small step-size produces small misadjustment, but at the cost of longer convergence time. Under time-varying environment, the optimum value of the step-size in FSS-LMS algorithm strikes a balance between the amount of lag noise and gradient noise [5]. However, the optimum value of step-size can not be determined a priori due to the unknown channel parameters. Therefore, in KVSS-LMS algorithm [10], the variable step-size (VSS) is attuned using

$$\begin{aligned} {\mu }'( n)=\bar{\alpha }{\mu }'( {n-1})+\bar{\gamma }\underline{\underline{e{ }^2( {n-1})}} \end{aligned}$$

(33)

In this KVSS-LMS algorithm, a large prediction error causes the step-size to increase in order to provide fast tracking, while a small prediction error leads to reduction in the step-size to yield small misadjustment. The step-size increases or decreases as the MSE increases or decreases, allowing the adaptive filter to track changes in the time-varying system, as well as to produce a small steady-state error. It also reduces sensitivity of the misadjustment to the level of nonstationarity. This approach is heuristically sound and has resulted in several ad hoc techniques, where the selection of convergence parameters is based on the magnitude of estimation error, polarity of the successive samples of the estimation error, measurement of the crosscorrelation of the estimation error with input data. However, the VSS-LMS algorithms are found to be sensitive to noise disturbances [4, 23] in the low signal-to-noise-ratio (SNR) environment because the step-size update of these algorithms are directly obtained from the instantaneous error that is contaminated by the disturbance noise.

Further in AVSS-LMS algorithm [1], the VSS is controlled using

$$\begin{aligned} {\mu }'( n)=\bar{\alpha }{\mu }'( {n-1})+\bar{\gamma }\theta ^2( {n-1}) \end{aligned}$$

(34)

$$\begin{aligned} \theta ( {n-1})=\bar{\alpha }_A \theta ( {n-2})+( {1-\bar{\alpha }_A })\underline{\underline{\left\{ {e( {n-1})e( {n-2})} \right\} }} \end{aligned}$$

(35)

Here, the error autocorrelation is usually a fine measure of the proximity to the optimum, which rejects the effect of uncorrelated noise sequence on the step-size update. In the early stages of adaptation, the error autocorrelation estimate is large, resulting in a large step-size. However, the small error autocorrelation leads to a small step-size under the optimum conditions. It results in effective adjustment of the step-size, while sustaining the immunity against independent noise disturbance, for the flexible control of misadjustment. The AVSS-LMS algorithm [1] shows substantial convergence rate improvement over the KVSS-LMS algorithm [10] and FSS-LMS algorithm [30] under the stationary environment for the low SNR, as well as the high SNR values. However, the performance of AVSS-LMS algorithm is comparable to the FSS-LMS and KVSS-LMS adaptive algorithms under the nonstationary conditions.

But in SVSS-LMS algorithm [2], the VSS is adjusted using the following recursive relation by adjusting the control parameters $\bar{\rho }_w \,\,and\,\,\bar{\alpha }_w$.

$$\begin{aligned} {\mu }'( n)={\mu }'( {n-1})+\bar{\rho }_w \vec {\psi }^T( n)\vec {x}( n)e( n) \end{aligned}$$

(36)

$$\begin{aligned} \vec {\psi }( n)=\bar{\alpha }_w \vec {\psi }( {n-1})+e( {n-1})\vec {x}( {n-1}) \end{aligned}$$

(37)

The above equation can be rewritten in the expanded form as

$$\begin{aligned} \begin{array}{l} \vec {\psi }^T\left\{ n \right\} =\bar{\alpha }_w^{\bar{Q}} \vec {\psi }^T\left\{ {n-\bar{Q}} \right\} +\bar{\alpha }_w^{\bar{Q}-1} e( {n-\bar{Q}})\vec {x}^T( {n-\bar{Q}})+\ldots \\ \qquad \qquad \qquad +\bar{\alpha }_w e( {n-2})\vec {x}^T( {n-2})+e( {n-1})\vec {x}^T( {n-1}) \\ \end{array} \end{aligned}$$

(38)

For $0\le \bar{\alpha }_w <1$ and $\bar{Q}\rightarrow high\,\,\,value$, the Eq. (38) can be approximated as

$$\begin{aligned} \begin{array}{l} \vec {\psi }^T\left\{ n \right\} \approx \underline{\underline{\bar{\alpha }_w^{\bar{Q}-1} e( {n-\bar{Q}})\vec {x}^T( {n-\bar{Q}})+}} \,\,\ldots \,\,\, \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{\underline{+\,\,\bar{\alpha }_w^2 e( {n-3})\vec {x}^T( {n-3})+\bar{\alpha }_w e( {n-2})\vec {x}^T( {n-2})+e( {n-1})\vec {x}^T( {n-1})}} \\ \end{array} \end{aligned}$$

(39)

This algorithm [2] outperforms the Mathews’ algorithm [13], when both are set to track the random walk channel under the similar conditions.