Logit tree models for discrete choice data with application to advice-seeking preferences among Chinese Christians

Abstract

Logit models are popular tools for analyzing discrete choice and ranking data. The models assume that judges rate each item with a measurable utility, and the ordering of a judge’s utilities determines the outcome. Logit models have been proven to be powerful tools, but they become difficult to interpret if the models contain nonlinear and interaction terms. We extended the logit models by adding a decision tree structure to overcome this difficulty. We introduced a new method of tree splitting variable selection that distinguishes the nonlinear and linear effects, and the variable with the strongest nonlinear effect will be selected in the view that linear effect is best modeled using the logit model. Decision trees built in this fashion were shown to have smaller sizes than those using loglikelihood-based splitting criteria. In addition, the proposed splitting methods could save computational time and avoid bias in choosing the optimal splitting variable. Issues on variable selection in logit models are also investigated, and forward selection criterion was shown to work well with logit tree models. Focused on ranking data, simulations are carried out and the results showed that our proposed splitting methods are unbiased. Finally, to demonstrate the feasibility of the logit tree models, they were applied to analyze two datasets, one with binary outcome and the other with ranking outcome.

Appendices

Appendix 1: Tree pruning: the cost-complexity algorithm

In the cost-complexity algorithm, we seek to find the optimal tree T by minimizing

$$\begin{aligned} R(T) + g |\tilde{T}|, \end{aligned}$$

(16)

where R(T) and $|\tilde{T}|$ are the cost function (or error) and the number of terminal nodes of the tree T respectively, and g controls the quantity of penalization for the tree size. The pruning stage can be divided into two steps: (1) generating subtrees and (2) choosing the best subtree. We will discuss them in the following Sections.

1.1 Generating subtrees

Before explaining how the subtrees are generated, here are some definitions:

• R(T) is defined as the sum of deviance (i.e. $-$2 $\times$ loglikelihood) for all of its terminal nodes.

• $T_t$ is the subtree with root t, where t is an internal node of tree T.

• R(t) is the deviance of internal node t.

• g(t) is the strength of the link from t and is defined as

  $$\begin{aligned} \frac{R(t)-R(T_t)}{|\tilde{T}_t|-1}. \end{aligned}$$

  It can be viewed as the reduction of error if the node t is further split instead of being stopped.

Note that when $g = g(t)$, it is indifferent for cutting the nodes under t or not.

After the growing stage, we arrive at a tree $T^0$. The pruning stage begins by calculating g(t) for all internal nodes in $T^0$ and searching for the node $t^1$ with the minimum value $g(t^1)$. Next, we then cut all the descendant nodes under $t^1$ and turn $t^1$ into a terminal node. A pruned tree $T^1$ is then created. This process is repeated until $T^0$ is pruned to the root $T^m$. Afterwards, we obtain a sequence of nested trees

$$\begin{aligned} T^0\supset T^1\supset T^2\supset \cdots \supset T^m. \end{aligned}$$

Note that among the sequence, the tree $T^y$ will be chosen as our final model if

$$\begin{aligned} g(t^y) \le g \le g(t^{y+1}). \end{aligned}$$

1.2 Choosing the best subtree

Breiman et al. (1984) suggested two methods to choose the best model among trees $T^0, T^1,\ldots ,T^m$. When the dataset is large, the independent testing dataset method can be used. Otherwise, the cross-validation method is suggested. Here, the latter method is applied.

To select the best subtree, we first need to compute the selection criterion, the cross-validation deviance (DEV-CV) The N observations are divided randomly into V arbitrary equal-sized subsets $L_1, L_2, \ldots , L_V$. It is a common practice to take $V=10$. For $v=1,\ldots ,V, L_v$ is the vth validation dataset and its complement $L_v^C$ is the vth training dataset. Based on the training dataset $L_v^C$, the vth sequence of nested trees,

$$\begin{aligned} T_v^0\supset T_v^1\supset T_v^2 \supset \cdots \supset T_v^{m_v} \end{aligned}$$

is constructed. We then use the validation dataset $L_v$ to compute the validation deviance. The validation deviance in any particular terminal node of tree $T_v^y, D_v^y$ is $-2 \times$ loglikelihood, where in the loglikelihood function, the probabilities are computed using $L_v^C$ and the observed frequencies are those in $L_v$ Adding up the validation deviance of all terminal nodes, we get the validation deviance of tree $T_v^y$.

After computing the validation deviances for all nested trees $T_v^0, T_v^1,\ldots ,T_v^{m_v}$, $v=1,\ldots ,V$, we can proceed to the next step, that is, evaluating the DEV-CV for each of the nested trees $T^0, T^1,\ldots ,T^m$. Breiman et al. (1984) recommended using the geometric average $\sqrt{g(t^y)g(t^{y+1})}$ as the estimate of $g^y$, and hence the cross-validation deviance for tree $T^y$, $R^{CV}(T^y)$ is evaluated as

$$\begin{aligned} R^{CV}(T^y) = \frac{1}{V}\sum _{v=1}^{V} R\left( T_v\left( \sqrt{g\left( t_v^y\right) g\left( t_v^{y+1}\right) }\right) \right) \end{aligned}$$

(17)

where $T_v(g)$ is equal to the pruned subtree $T_v^y$ such that $g(t_v^y) \le g \le g(t_v^{y+1})$.

Now we can return to the selection of the best subtree from $T^0, T^1,\ldots ,T^m$. Let $T^*$ be the tree with minimum DEV-CV. It sounds reasonable to select $T^*$ as our final model. Since the position of the minimum $R^{CV}(T^*)$ is uncertain (Breiman et al. 1984), we adopt the 1-SE rule to select another tree $T^{**}$ as our final model. $T^{**}$ is the smallest subtree which satisfies

$$\begin{aligned} R^{CV}(T^{**}) \le R^{CV}(T^*) + SE\left( R^{CV}(T^*)\right) . \end{aligned}$$

(18)

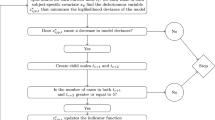
To summarize, below is the pseudo-code for demonstrating how our pruning algorithm works:

Appendix 2: Covariates used in the “formation and transformation of beliefs in Chinese” study

The summary statistics of these covariates are listed in Table 14.

Table 14 Summary of covariates

All these covariates, with the exception of demographic information, are the participants’ raw answers to a number of items. The meaning of these covariates will be described in the following.

Personality. The 50-item International Personality Item Pool Big-Five Domain scale (IPIP; Goldberg 1997) was used to measure five personality dimensions, namely intellect (openness to experience), conscientiousness, extraversion, agreeableness, and emotional stability. The items were translated into Chinese (followed by the usual back-translation procedure). Participants rated each item on a 5-point scale (1 $=$ extremely disagree; 5 $=$ extremely agree). The Cronbach’s alpha for the five dimensions in our sample were 0.79, 0.76, 0.86, 0.77, and 0.90 respectively.

Social axiom. Social Axiom (Leung et al. 2002) included social cynicism (negative assessment of human nature and social events), social complexity (belief in multiple and uncertain solutions to social issues), reward for application (belief that effort will bring good outcomes), religiosity (belief in the presence of supernatural influences on the world, and that religions are good), and fate control (belief in the presence of impersonal forces influencing social events). Participants rated each of the 25 items on a 5-point scale (1 $=$ extremely disagree; 5 $=$ extremely agree). The Cronbach’s alpha for the five dimensions in our sample were 0.61, 0.56, 0.71, 0.76, and 0.71 respectively.

Quality of life. From the 28 items in the Hong Kong Chinese version of World Health Organization Quality of Life Measures (WHOQOL-BREF(HK); Leung et al. 1997) we chose 26 which we deemed suitable. The instrument provides several indices, namely Physical Health, Psychological Health (culturally adjusted for Hong Kong), Social Relationships, and Environment. Overall quality of life and overall health were individually indicated by one item each. Participants responded to each item on a 5-point scale. The anchors of the rating scales vary from item to item, using wordings from the items themselves. For example, for the item “How safe do you feel in your daily life?”, the scale was from 1 (not at all safe) to 5 (extremely safe).To allow comparison with the WHOQOL-100 (the origin of WHOQOL-BREF(HK)), the 6 indices (Physical health, Psychological health, Social relationships, Environment, Overall QOL, Overall health) were scaled to the range (4, 20). The Cronbach’s alpha for the four dimensions in our sample were 0.67, 0.82, 0.59, and 0.68 respectively.

Personal values. Personal values were measured with the Schwartz Value Survey (Schwartz 1996). Participants indicated the importance of each of 57 items as a guiding principle in their life on a 9-point scale ($-$1 $=$ opposed to my values; 0 $=$ not important, 7 $=$ of extreme importance). Ten value indices were computed: conformity, tradition, benevolence, universalism, self-direction, stimulation, hedonism, achievement, power, and security. The Cronbach’s alpha for the ten dimensions in our sample were 0.77, 0.56, 0.83, 0.84, 0.77, 0.64, 0.58, 0.81, 0.76, and 0.76 respectively.

Faith maturity. Faith Maturity Scale (FMS) was developed by the Search Institute (http://www.search-institute.org/). The scale has two dimensions. The FM vertical dimension reflects the person and his/her feelings of faith. The FM horizontal dimension reflects how the person’s behavior towards others approximates that prescribed in the religion. The Cronbach’s alpha for the two dimensions in our sample were 0.89 and 0.77 respectively.

Demographic information. Participants indicated if they were students, and for how long they had been a believer.