Analytical computation of gravity effects for polyhedral bodies

Abstract

On the basis of recent analytical results we derive new formulas for computing the gravity effects of polyhedral bodies which are expressed solely as function of the coordinates of the vertices of the relevant faces. We thus prove that such formulas exhibit no singularity whenever the position of the observation point is not aligned with an edge of a face. In the opposite case, the contribution of the edge to the potential to its first-order derivative and to the diagonal entries of the second-order derivative is deemed to be zero on the basis of some claims which still require a rigorous mathematical proof. In contrast with a common statement in the literature, it is proved that only the off-diagonal entries of the second-order derivative of the potential do exhibit a noneliminable singularity when the observation point is aligned with an edge of a face. The analytical provisions on the range of validity of the derived formulas have been fully confirmed by the Matlab$^{\textregistered }$ program which has been coded and thoroughly tested by computing the gravity effects induced by real asteroids at arbitrarily placed observation points.

Appendices

Appendix 1

The aim of this appendix was to illustrate some useful geometrical results concerning a generic face.

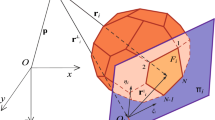
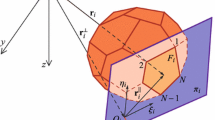
In particular, we shall detail the algorithm which has been implemented to evaluate the columns of the operator ${\mathbf T}_{F_i}$ in (7) and project the observation point onto the generic face so as to determine the origin $P_i$ of the 2D reference frame on the face, see, e.g. Fig. 2.

For a generic face, which is defined at least by three vertices, we know the coordinates of the relevant 3D vectors, say ${\mathbf r}^i_1$, ${\mathbf r}^i_2$ and ${\mathbf r}^i_3$ where, for a face with more than three vertices, the subscript 3 denotes $N_{E_i}$; hence, we always consider as third vector the position vector of the last vertex of the face.

The unit normal to the face $F_i$ can be evaluated as

$$\begin{aligned} {\mathbf n}_i=\frac{({\mathbf r}_{i2}-{\mathbf r}_{i1})\times ({\mathbf r}_{i3}-{\mathbf r}_{i1})}{|({\mathbf r}_{i2}-{\mathbf r}_{i1})\times ({\mathbf r}_{i3}-{\mathbf r}_{i1})|}, \end{aligned}$$

(51)

where $\times$ denotes the vector product and the order of vectors in it depends on the circulation sense assumed along $Fr(F_i)$; specifically, we have assumed that the vertices of each face are numbered consecutively in a counter-clockwise sense as seen from an observer lying outside $\varOmega$.

Denoting by

$$\begin{aligned} {\mathbf u}_i=\frac{({\mathbf r}_{i2}-{\mathbf r}_{i1})}{|({\mathbf r}_{i2}-{\mathbf r}_{i1})|} \end{aligned}$$

(52)

we also compute

$$\begin{aligned} {\mathbf v}_i={\mathbf n}_i\times {\mathbf u}_i \end{aligned}$$

(53)

Thus ${\mathbf v}_i$ is parallel to the face and, together with ${\mathbf u}_i$, defines the 2D reference frame on the face, see Fig. 2, as well as the operator ${\mathbf T}_{F_i}$ in (7)

$$\begin{aligned} {\mathbf T}_{F_i}= \left[ \begin{array}{c@{\quad }c} {\mathbf u}_{i1}&{}{\mathbf v}_{i1}\\ {\mathbf u}_{i2}&{}{\mathbf v}_{i2}\\ {\mathbf u}_{i3}&{}{\mathbf v}_{i3} \end{array} \right] \end{aligned}$$

(54)

Given an arbitrary vector ${\mathbf p}$, representing the observation point $P$, our aim is to obtain the 3D coordinates of the point ${\mathbf p}_{F_i}$ representing the orthogonal projection $P_i$ of $P$ onto the face $F_i$.

It is customary to choose $P$ as the origin of the 3D reference frame in which the coordinates of the vertices of the polyhedron are assigned; hence ${\mathbf p}={\mathbf o}$. Nevertheless, for generality, we shall make reference in the sequel to an arbitrary position ${\mathbf p}$ of the observation point.

The equation of the face $F_i$ is defined in parametric form by

$$\begin{aligned} {\mathbf r}_i(\xi ,\eta )={\mathbf r}_{i1}+\xi {\mathbf u}_i+\eta {\mathbf v}_i \end{aligned}$$

(55)

or, in implicit form, as

$$\begin{aligned} {\mathbf r}_i\cdot {\mathbf n}_i={\mathbf r}_{i1}\cdot {\mathbf n}_i=c_i \end{aligned}$$

(56)

The parametric equation of the line passing through ${\mathbf p}$ and directed along ${\mathbf n}_i$ is

$$\begin{aligned} {\mathbf r}(\lambda )={\mathbf p}+\lambda {\mathbf n}_i \end{aligned}$$

(57)

Accordingly, the value $\lambda ^*$ such that ${\mathbf r}(\lambda ^*)\in F_i$ is trivially obtained by imposing the fulfillment of (56)

$$\begin{aligned} ({\mathbf p}+\lambda ^*{\mathbf n}_i)\cdot {\mathbf n}_i=c_i \end{aligned}$$

(58)

from which one infers

$$\begin{aligned} \lambda ^* = c_i-{\mathbf p}\cdot {\mathbf n}_i = ({\mathbf r}_{i1}-{\mathbf p})\cdot {\mathbf n}_i \end{aligned}$$

(59)

being ${\mathbf n}_i\cdot {\mathbf n}_i=1$.

In conclusion

$$\begin{aligned} {\mathbf p}_{F_i}&= {\mathbf r}(\lambda ^*) = {\mathbf p}+\lambda ^*{\mathbf n}_i = {\mathbf p}+(c_i-{\mathbf p}\cdot {\mathbf n}_i){\mathbf n}_i \nonumber \\&= {\mathbf p}+[({\mathbf r}_{i1}-{\mathbf p})\cdot {\mathbf n}_i)]{\mathbf n}_i \nonumber \\&= {\mathbf p}+({\mathbf n}_i\otimes {\mathbf n}_i)({\mathbf r}_{i1}-{\mathbf p}) \end{aligned}$$

(60)

so that

$$\begin{aligned} d_i=({\mathbf r}_{i1}-{\mathbf p})\cdot {\mathbf n}_i \end{aligned}$$

(61)

represent the signed distance of $P$ from the face $F_i$.

Appendix 2

Let us consider a prism and suppose that the observation point $P$ does belong to the interior of one of its faces. Without loss of generality we shall assume that the point belongs to the face having unit normal directed in the opposite direction with respect to the x axis, see, e.g. Fig. 6.

Fig. 6

Prism used for computing analytically the off-diagonal entries of the second derivative of the potential

The position of $P$ with respect to the face is defined by the positive quantities $b_1$, $b_2$, $c_1$ and $c_2$ so that the lengths of the edges parallel to the $y$ and $z$ axes are expressed by $b= b_1+b_2$ and $c= c_1+c_2$, respectively.

For brevity we shall detail only the computation of the integrals pertaining to the edges of the first face; for this reason we report in Fig. 7 only the relevant local reference frame.

Fig. 7

First face of the prism in Fig. 6 and related local reference frame

Thus, the 2D position vectors of the vertices are

$$\begin{aligned} \begin{array}{l} {\varvec{\rho }}_1 = \left[ \begin{array}{c} b_1\\ -c_2 \end{array} \right] \quad {\varvec{\rho }}_2 = \left[ \begin{array}{c} b_1\\ c_1 \end{array} \right] \\ {\varvec{\rho }}_3 = \left[ \begin{array}{c} -b_2\\ c_1 \end{array} \right] \quad {\varvec{\rho }}_4 = \left[ \begin{array}{c} -b_2\\ -c_2 \end{array} \right] \end{array} \end{aligned}$$

(62)

so that

$$\begin{aligned} \begin{array}{l} {\varvec{\rho }}_2-{\varvec{\rho }}_1 = \left[ \begin{array}{c} 0\\ c \end{array} \right] \quad {\varvec{\rho }}_3-{\varvec{\rho }}_2 = \left[ \begin{array}{c} -b\\ 0 \end{array} \right] \\ {\varvec{\rho }}_4-{\varvec{\rho }}_3 = \left[ \begin{array}{c} 0\\ -c \end{array} \right] \quad {\varvec{\rho }}_1-{\varvec{\rho }}_4 = \left[ \begin{array}{c} b\\ 0 \end{array} \right] \end{array} \end{aligned}$$

(63)

Accordingly, one infers from (11)

$$\begin{aligned} \begin{array}{l} p_1\!=\!c^2 \qquad q_1\!=\!-\!c_2c \qquad u_1=b_1^2\!+\!c_2^2 \\ v_1\!=\!a^2+b_1^2\!+\!c_2^2 \qquad p_1\!+\!2q_1\!+\!v_1\!=\!a^2+b_1^2+c_1^2\quad \end{array} \end{aligned}$$

(64)

for the first edge

$$\begin{aligned} \begin{array}{l} p_2=b^2 \qquad q_2=-b_1b \qquad u_2=b_1^2+c_1^2 \\ v_2=a^2+b_1^2+c_1^2 \qquad p_2+2q_2+v_2=a^2+b_2^2+c_1^2 \end{array} \end{aligned}$$

(65)

for the second edge

$$\begin{aligned} \begin{array}{l} p_3=c^2 \qquad q_3=-c_1c \qquad u_3=b_2^2+c_1^2 \\ v_3=a^2+b_2^2+c_1^2 \qquad p_3+2q_3+v_3=a^2+b_2^2+c_2^2 \end{array} \end{aligned}$$

(66)

for the third edge and

$$\begin{aligned} \begin{array}{l} p_4=b^2 \qquad q_4=-b_2b \qquad u_4=b_2^2+c_1^2 \\ v_4=a^2+b_2^2+c_1^2 \qquad p_4+2q_4+v_4=a^2+b_1^2+c_2^2 \end{array} \end{aligned}$$

(67)

for the fourth edge.

Being also

$$\begin{aligned} \begin{array}{l} {\varvec{\nu }}_{F_1,1} = \left[ \begin{array}{c} 1\\ 0 \end{array} \right] \quad {\varvec{\nu }}_{F_1,2} = \left[ \begin{array}{c} 0\\ 1 \end{array} \right] \\ {\varvec{\nu }}_{F_1,3} = \left[ \begin{array}{c} -1\\ 0 \end{array} \right] \quad {\varvec{\nu }}_{F_1,4} = \left[ \begin{array}{c} 0\\ -1 \end{array} \right] \end{array} \end{aligned}$$

(68)

one has from (39)

$$\begin{aligned} {\varvec{\iota }}_{F_1,1} = \left[ \begin{array}{c} K_{F_1,1}-K_{F_1,3}\\ K_{F_1,2}-K_{F_1,4} \end{array} \right] , \end{aligned}$$

(69)

where

$$\begin{aligned} \begin{array}{l} K_{F_1,1} = \displaystyle {\ln \frac{c_1+\sqrt{a^2+b_1^2+c_1^2}}{-c_2+\sqrt{a^2+b_1^2+c_2^2}} } \\ K_{F_1,2} = \displaystyle {\ln \frac{b_2+\sqrt{a^2+b_2^2+c_1^2}}{-b_1+\sqrt{a^2+b_1^2+c_1^2}} } \\ K_{F_1,3} = \displaystyle {\ln \frac{c_2+\sqrt{a^2+b_2^2+c_2^2}}{-c_1+\sqrt{a^2+b_2^2+c_1^2}} } \\ K_{F_1,4} = \displaystyle {\ln \frac{b_1+\sqrt{a^2+b_1^2+c_2^2}}{-b_2+\sqrt{a^2+b_2^2+c_2^2}} } \end{array} \end{aligned}$$

(70)

which are trivially well defined.

For the reader’s convenience we also report the final expressions of the remaining integrals.

Specifically, it turns out to be

$$\begin{aligned} {\varvec{\iota }}_{F_2,1} = \left[ \begin{array}{c} K_{F_2,1}-K_{F_2,3}\\ K_{F_2,2}-K_{F_2,4} \end{array} \right] , \end{aligned}$$

(71)

where

$$\begin{aligned} \begin{array}{l} K_{F_2,1} = \displaystyle {\ln \frac{b_2+\sqrt{b_2^2+c_2^2}}{-b_1+\sqrt{b_1^2+c_2^2}} } \\ K_{F_2,2} = \displaystyle {\ln \frac{c_1+\sqrt{b_2^2+c_1^2}}{-c_2+\sqrt{b_2^2+c_2^2}} } \\ K_{F_2,3} = \displaystyle {\ln \frac{b_1+\sqrt{b_1^2+c_1^2}}{-b_2+\sqrt{b_2^2+c_1^2}} } \\ K_{F_2,4} = \displaystyle {\ln \frac{c_2+\sqrt{b_1^2+c_2^2}}{-c_1+\sqrt{b_1^2+c_1^2}} } \end{array} \end{aligned}$$

(72)

for the second face;

$$\begin{aligned} {\varvec{\iota }}_{F_3,1} = \left[ \begin{array}{c} K_{F_3,1}-K_{F_3,3}\\ K_{F_3,2}-K_{F_3,4} \end{array} \right] , \end{aligned}$$

(73)

where

$$\begin{aligned} \begin{array}{l} K_{F_3,1} = \displaystyle {\ln \frac{a+\sqrt{a^2+b_1^2+c_1^2}}{\sqrt{b_1^2+c_1^2}} } \\ K_{F_3,2} = \displaystyle {\ln \frac{c_2+\sqrt{a^2+b_1^2+c_2^2}}{-c_1+\sqrt{a^2+b_1^2+c_1^2}} } \\ K_{F_3,3} = \displaystyle {\ln \frac{\sqrt{b_1^2+c_2^2}}{-a+\sqrt{a^2+b_1^2+c_2^2}} } \\ K_{F_3,4} = \displaystyle {\ln \frac{c_1+\sqrt{b_1^2+c_1^2}}{-c_2+\sqrt{b_1^2+c_2^2}} } \end{array} \end{aligned}$$

(74)

for the third face;

$$\begin{aligned} {\varvec{\iota }}_{F_4,1} = \left[ \begin{array}{c} K_{F_4,3}-K_{F_4,1}\\ K_{F_4,2}-K_{F_4,4} \end{array} \right] , \end{aligned}$$

(75)

where

$$\begin{aligned} \begin{array}{l} K_{F_4,1} = \displaystyle {\ln \frac{a+\sqrt{a^2+b_2^2+c_1^2}}{\sqrt{b_2^2+c_1^2}} } \\ K_{F_4,2} = \displaystyle {\ln \frac{c_2+\sqrt{a^2+b_2^2+c_2^2}}{-c_1+\sqrt{a^2+b_2^2+c_1^2}} } \\ K_{F_4,3} = \displaystyle {\ln \frac{\sqrt{b_2^2+c_2^2}}{-a+\sqrt{a^2+b_2^2+c_2^2}} } \\ K_{F_4,4} = \displaystyle {\ln \frac{c_1+\sqrt{b_2^2+c_1^2}}{-c_2+\sqrt{b_2^2+c_2^2}} } \end{array} \end{aligned}$$

(76)

for the fourth face;

$$\begin{aligned} {\varvec{\iota }}_{F_5,1} = \left[ \begin{array}{c} K_{F_5,4}-K_{F_5,2}\\ K_{F_5,1}-K_{F_5,3} \end{array} \right] \!, \end{aligned}$$

(77)

where

$$\begin{aligned} \begin{array}{l} K_{F_5,1} = \displaystyle {\ln \frac{\sqrt{b_1^2+c_1^2}}{-a+\sqrt{a^2+b_1^2+c_1^2}} } \\ K_{F_5,2} = \displaystyle {\ln \frac{b_2+\sqrt{b_2^2+c_1^2}}{-b_1+\sqrt{b_1^2+c_1^2}} } \\ K_{F_5,3} = \displaystyle {\ln \frac{a+\sqrt{a^2+b_2^2+c_1^2}}{\sqrt{b_2^2+c_1^2}} } \\ K_{F_5,4} = \displaystyle {\ln \frac{b_1+\sqrt{a^2+b_1^2+c_1^2}}{-b_2+\sqrt{a^2+b_2^2+c_1^2}} } \end{array} \end{aligned}$$

(78)

for the fifth face;

$$\begin{aligned} {\varvec{\iota }}_{F_6,1} = \left[ \begin{array}{c} K_{F_6,1}-K_{F_6,3}\\ K_{F_6,2}-K_{F_6,4} \end{array} \right] \!, \end{aligned}$$

(79)

where

$$\begin{aligned}&K_{F_6,1} = \displaystyle {\ln \frac{b_2+\sqrt{b_2^2+c_2^2}}{-b_1+\sqrt{b_1^2+c_2^2}} } \nonumber \\&K_{F_6,2} = \displaystyle {\ln \frac{a+\sqrt{a^2+b_2^2+c_2^2}}{\sqrt{b_2^2+c_2^2}} } \nonumber \\&K_{F_6,3} = \displaystyle {\ln \frac{b_1+\sqrt{a^2+b_1^2+c_2^2}}{-b_2+\sqrt{a^2+b_2^2+c_2^2}} } \nonumber \\&K_{F_6,4} = \displaystyle {\ln \frac{\sqrt{b_1^2+c_2^2}}{-a+\sqrt{a^2+b_1^2+c_2^2}} } \end{aligned}$$

(80)

for the sixth face.

The application of the previous formula to point $P_c$ in Fig. 3 yields the numerical results reported in Table 1.

As a final remark we emphasize that the previous formulas give further account of the singularity which can characterize the off-diagonal entries of the second derivative when the observation point is aligned with one of the edges of a face.

In the example of Fig. 6 the observation point does belong to the second face so that we need to make reference to the quantities $K_{F_2,j}, \, j=(1,\dots ,4)$ in (72).

It is apparent that whenever $P$ in Fig. 6 tends to become aligned with one edge, i.e. one of the four quantities $b_1$, $b_2$, $c_1$, $c_2$ tends to zero, one of the four expressions in (72) becomes undefined since one of the four denominators vanishes.

Due to space limitations the analytical evaluation of the integrals $I_{F_i}$ and $J_{F_i}$ for the prism of Fig. 6, with constant or linearly varying density, will be reported elsewhere so as to extend the results contributed in García-Abdeslem (1992) and García-Abdeslem (2005).