Abstract
In a partition model, we show that each maximin individually rational and ex ante maximin efficient allocation of a single good economy is implementable as a maximin equilibrium. When there are more than one good, we introduce three conditions. If none of the three conditions is satisfied, then a maximin individually rational and ex ante maximin efficient allocation may not be implementable. However, as long as one of the three conditions is satisfied, each maximin individually rational and ex ante maximin efficient allocation is implementable. Our work generalizes and extends the recent paper of de Castro et al. (Games Econ Behav 2015. doi:10.1016/j.geb.2015.10.010).




Similar content being viewed by others
Notes
A related work is done by Bosmans and Ooghe (2013). They showed that maximin is the only criterion satisfying anonymity, continuity, weak Pareto and weak Hammond equity.
This assumption is without loss of generality, since if there exist two different states \(\omega \) and \(\omega ^{\prime }\), such that no agent is able to distinguish them, then the two states may as well be treated as one state.
For each fixed \(\omega \), we have \(u_{i}\left( c_{i}; \omega \right) < u_{i}\left( c_{i}+\epsilon ; \omega \right) \), whenever \(\epsilon \) is a none zero vector in \(\mathbb {R}^{\ell }_{+}\).
See also de Castro et al. (2015).
In addition to the fact that there is no longer a conflict between efficiency and incentive compatibility under the maximin preferences, the adoption of these preferences provides new insights and superior outcomes than the Bayesian preferences as it has been shown in Angelopoulos and Koutsougeras (2015), Bodoh-Creed (2012), Bose et al. (2006), de Castro and Yannelis (2009), Castro et al. (2011), de Castro et al. (2015), Gollier (2014), He and Yannelis (2015), Koufopoulos and Kozhan (2016), Liu (2014), Ohtaki and Ozaki (2015), Traeger (2014), just to name a few. Furthermore, the maximin preferences solve the Ellsberg Paradox (see, e.g., Castro and Yannelis (2013)). Interestingly, ambiguity does not necessarily vanish through statistical learning in an one-urn environment (Zimper and Ma (2016)).
Indeed, in the standard type model, each agent i has a type set \(T_{i}\), and the set of states of nature is \(T=T_{1}\times \cdots \times T_{N}\). Let \(T_{i}=F_{i}\) and \(T=\Omega \), then we have \(T=T_{1}\times \cdots \times T_{N}\) because of Assumption 5. That is, if a partition model satisfies Assumption 5, then it can be represented by the standard type model.
In this paper, an agent cannot distinguish the states of nature within an event \(E^{\mathcal {F}_{i}}\in \mathcal {F}_{i}\).
The robust control approach presumes that decision makers are able to specify the set of possible models, but are either unable or unwilling to form a prior over the forms of model misspecification.
Aryal and Stauber (2014) introduced the notions of \(\epsilon \)-perfect maxmin equilibrium, perfect maxmin equilibrium and robust sequential equilibrium. Their notions allow players to make small mistakes which is not the case with our notion of maximin equilibrium.
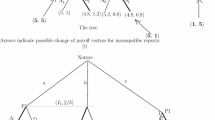
Notice that both path ‘\(ac_{1}b_{2}\)’ and path ‘\(bc_{1}b_{2}\)’ lead to incompatible reports. Therefore, the actual redistribution of player 1 is \(\min _{\omega ^{\prime }\in \Omega }\left\{ x_{1}\left( \omega ^{\prime }\right) -e_{1}\left( \omega ^{\prime }\right) \right\} =-0.2\).
We assume that a player lies, only if he can benefit from doing so.
Notice that \(\tilde{\omega }\in E^{\mathcal {F}_{i}}\), and
$$\begin{aligned} v_{i}\left( E^{\mathcal {F}_{i}}, E_{-i}^{*}; \omega ^{*}\right)= & {} \min _{\mathop {\omega ^{\prime }\in E^{\mathcal {F}_{i}}}\limits ^{E^{\mathcal {F}_{-i}}\in \mathcal {F}_{-i};} }\left\{ v_{i}\left( E^{\mathcal {F}_{i}}, E^{\mathcal {F}_{-i}}; \omega ^{\prime }\right) \right\} \le \min _{ \omega ^{\prime }\in E^{\mathcal {F}_{i}}}\left\{ v_{i}\left( E^{\mathcal {F}_{i}}, E^{\mathcal {F}_{-i}}\left( \omega ^{\prime }\right) ; \omega ^{\prime }\right) \right\} \\\le & {} v_{i}\left( E^{\mathcal {F}_{i}}, E^{\mathcal {F}_{-i}}\left( \tilde{\omega }\right) ; \tilde{\omega }\right) =u_{i}\left( x_{i}\left( \tilde{\omega }\right) ; \tilde{\omega }\right) , \end{aligned}$$imply that we must have equality throughout.
Since by the definition of a minimum, we have that
$$\begin{aligned} \min _{\mathop {\omega ^{\prime }\in E^{\mathcal {F}_{i}}}\limits ^{E^{\mathcal {F}_{-i}}\in \mathcal {F}_{-i};} }\left\{ v_{i}\left( \tilde{E}^{\mathcal {F}_{i}}, E^{\mathcal {F}_{-i}}; \omega ^{\prime }\right) \right\} \le \min _{ \omega ^{\prime }\in E^{\mathcal {F}_{i}}}\left\{ v_{i}\left( \tilde{E}^{\mathcal {F}_{i}}, E^{\mathcal {F}_{-i}}\left( \omega ^{\prime }\right) ; \omega ^{\prime }\right) \right\} . \end{aligned}$$.
In words, (10) says that if all the other players are truthful, then player i can ensure a higher lower bound payoff by lying under the event \(E^{\mathcal {F}_{i}}\).
In other words, truth telling for all i turns out to be a fixed point.
To avoid confusion, it is worthwhile to re-emphasize that different \(\omega ^{\prime }\in \arg \min _{ \omega ^{''}\in E^{\mathcal {F}_{i}}}\left\{ u_{i}\left( x_{i}\left( \omega ^{''}\right) ; \omega ^{''}\right) \right\} \) may be matched with a different \(\tilde{\omega }\).
Recall that both the initial endowment and the utility function are \(\mathcal {F}_{i}\)-measurable.
When player 1 is in the event \(\left\{ a, b\right\} \), the worst net transfer for him is \(x_{1}\left( f\right) -e_{1}\left( f\right) \). He may get the worst transfer if the players’ reports are not compatible, or if the agreed state is f. The lie \(\left\{ c, d, e\right\} \) allows him to avoid the worst net transfer, and gives him the highest lower bound payoff. Indeed, reporting \(\left\{ a, b\right\} \) gives him a payoff of
$$\begin{aligned}&\min \left\{ v_{1}\left( \left\{ a, b\right\} , \left\{ a, c\right\} ; a\right) , v_{1}\left( \left\{ a, b\right\} , \left\{ b, d\right\} ; a\right) , v_{1}\left( \left\{ a, b\right\} , \left\{ e, f\right\} ; a\right) , \right. \\&\qquad \left. v_{1}\left( \left\{ a, b\right\} , \left\{ a, c\right\} ; b\right) , v_{1}\left( \left\{ a, b\right\} , \left\{ b, d\right\} ; b\right) , v_{1}\left( \left\{ a, b\right\} , \left\{ e, f\right\} ; b\right) \right\} \\&\quad =\min \left\{ 6.32455, 6.32455, 5.66239, 6.32455, 6.32455, 5.66239\right\} =5.66239; \end{aligned}$$reporting \(\left\{ c, d, e\right\} \) gives him a payoff of
$$\begin{aligned} \min \left\{ 6.32455, 6.32297, 6.32258, 6.32455, 6.32297, 6.32258\right\} =6.32258; \end{aligned}$$and reporting \(\left\{ f\right\} \) gives him a payoff of
$$\begin{aligned} \min \left\{ 5.66239, 5.66239, 5.66239, 5.66239, 5.66239, 5.66239\right\} =5.66239. \end{aligned}$$Clearly, the payoff of reporting \(\left\{ c, d, e\right\} \) is the highest.
That is, the mechanism designer has a private information set which consists of singletons.
References
Angelopoulos, A., Koutsougeras, L.C.: Value allocation under ambiguity. Econ. Theory 59(1), 147–167 (2015)
Aryal, G., Stauber, R.: Trembles in extensive games with ambiguity averse player. Econ. Theory 57(1), 1–40 (2014)
Baliga, S., Corchón, L., Sjöström, T.: The theory of implementation when the planner is a player. J. Econ. Theory 77, 15–33 (1997)
Bergemann, D., Morris, S.: Robust implementation in direct mechanisms. Rev. Econ. Stud. 76, 1175–1204 (2009)
Bodoh-Creed, A.: Ambiguous beliefs and mechanism design. Games Econ. Behav. 75, 518–537 (2012)
Bose, S., Ozdenoren, E., Pape, A.: Optimal auctions with ambiguity. Theor. Econ. 1, 411–438 (2006)
Bosmans, K., Ooghe, E.: A characterization of maximin. Econ. Theory Bull. 1(2), 151–156 (2013)
Chakravorty, B., Corchón, L., Wilkie, S.: Credible implementation. Games Econ. Behav. 57(1), 18–36 (2006)
Dasgupta, P.S., Hammond, P.J., Maskin, E.S.: The implementation of social choice rules: some general results on incentive compatibility. Rev. Econ. Stud. 46(2), 185–216 (1979)
de Castro, L.I., Yannelis, N.C.: Ambiguity aversion solves the conflict between efficiency and incentive compatibility, working paper (2009)
de Castro, L.I., Yannelis, N.C.: An interpretation of Ellsbergs Paradox based on information and incompleteness. Econ. Theory Bull. 1(2), 139–144 (2013)
de Castro, L.I., Pesce, M., Yannelis, N.C.: Core and equilibria under ambiguity. Econ. Theory 48, 519–548 (2011)
de Castro, L.I., Liu, Z., Yannelis, N.C.: Implementation under ambiguity. Games Econ. Behav. (2015). doi:10.1016/j.geb.2015.10.010
de Castro, L.I., Liu, Z., Yannelis, N.C.: Relationship between partition and type model in general equilibrium with asymmetric information, working paper (2016)
de Castro, L.I., Pesce, M., Yannelis, N.C.: Rational expectations under Ambiguity, working paper (2015)
Gilboa, I., Schmeidler, D.: Maxmin expected utility with non-unique prior. J. Math. Econ. 18(2), 141–153 (1989)
Glycopantis, D., Muir, A., Yannelis, N.C.: An extensive form interpretation of the private core. Econ. Theory 18, 293–319 (2001)
Glycopantis, D., Muir, A., Yannelis, N.C.: On extensive form implementation of contracts in differential information economies. Econ. Theory 21, 495–526 (2003)
Gollier, C.: Optimal insurance design of ambiguous risks. Econ. Theory 57(3), 555–576 (2014)
Guo, H., Yannelis, N.C.: Ambiguous and robust full implementation, working paper (2015)
Hahn, G., Yannelis, N.C.: Coalitional Bayesian Nash implementation in differential information economies. Econ. Theory 18, 485–509 (2001)
Hansen, L.P., Sargent, T.J.: Acknowledging misspecification in macroeconomic theory. Rev. Econ. Dyn. 4, 519–535 (2001)
He, W., Yannelis, N.C.: Equilibrium theory under ambiguity. J. Math. Econ. 61, 86–95 (2015)
Holmström, B., Myerson, R.B.: Efficient and durable decision rules with incomplete information. Econometrica 51(6), 1799–1819 (1983)
Jackson, M.O.: Bayesian implementation. Econometrica 59(2), 461–477 (1991)
Koufopoulos, K., Kozhan, R.: Optimal insurance under adverse selection and ambiguity aversion. Econ. Theory 62(4), 659–687 (2016)
Liu, Z.: A note on the welfare of the maximin rational expectations. Econ. Theory Bull. 2, 213–218 (2014)
Liu, Z.: Implementation of maximin rational expectations equilibrium. Econ. Theory 62(4), 813–837 (2016)
Ohtaki, E., Ozaki, H.: Monetary equilibria and Knightian uncertainty. Econ. Theory 59(3), 435–459 (2015)
Palfrey, T.R., Srivastava, S.: On Bayesian implementable allocations. Rev. Econ. Stud. 54(2), 193–208 (1987)
Palfrey, T.R., Srivastava, S.: Implementation with incomplete information in exchange economies. Econometrica 57(1), 115–134 (1989)
Traeger, C.P.: Why uncertainty matters: discounting under intertemporal risk aversion and ambiguity. Econ. Theory 56(3), 627–664 (2014)
Wald, A.: Statistical Decision Functions. John Wiley and Sons, New York (1950)
Yannelis, N.C.: The Core of an economy with differential information. Econ. Theory 1, 183–198 (1991)
Zimper, A., Ma, W.: Bayesian learning with multiple priors and nonvanishing ambiguity. Econ. Theory (2016). doi:10.1007/s00199-016-1007-y
Author information
Authors and Affiliations
Corresponding author
Additional information
Different versions of this paper were presented at the University of Queensland, Australian Econometric Society meetings, SWET conference, Paris, University of Glasgow, Midwest Economic Theory Meetings at Lawrence, USC, University of St Andrews, UC-Davis, UIBE, Johns Hopkins University, UC-Santa Barbara, Ecole Polytechnique, SAET conference, Portugal, Rice University and the NBER/GE conference at Indiana. We have greatly benefited from comments, discussions and suggestions by many participants in the above presentations, and a referee. Special thanks to Filipe Marins da Rocha who read earlier versions of this paper and whose suggestions lead to the current one. Liu gratefully acknowledges the funding from NSFC No. 71571122; the funding from the Research and Innovation Centre of Metropolis Economic and Social Development, Capital University of Economics and Business; and the funding from the humanities university project of China University of Political Science and Law.
Rights and permissions
About this article
Cite this article
de Castro, L.I., Liu, Z. & Yannelis, N.C. Ambiguous implementation: the partition model. Econ Theory 63, 233–261 (2017). https://doi.org/10.1007/s00199-016-1023-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00199-016-1023-y