Abstract
The class of rank-additive social welfare orders (RA SWOs) includes rank-weighted utilitarian, generalized utilitarian, and rank-discounted generalized utilitarian rules; it is a flexible framework for population ethics. This paper axiomatically characterizes RA SWOs and studies their properties in two frameworks: the actualist framework (which only tracks the utilities of people who actually exist) and the possibilist framework (which also assigns zero utilities to people who don’t exist). The axiomatizations and properties are quite different in the two frameworks. For example, actualist RA SWOs can simultaneously evade the Repugnant Conclusion and promote equality, whereas in the possibilist framework, there is a trade-off between these two desiderata. On the other hand, possibilist RA SWOs satisfy the Positive expansion and Negative expansion axioms, whereas the actualist ones don’t.


Similar content being viewed by others
Notes
The term “SWO” is somewhat misleading, because this ordering may encode ethical judgements over population size in addition to ethical judgements over welfare. But I use it because it is standard. In the literature on population ethics, such orderings are also called population principles or population axiologies.
In these assessments, it is important that we work with lifetime utilities, not momentary utilities. Thus, a judgement that “It would be ethically better if Alice did not exist” does not imply that Alice should die—rather, it means it would have been better if Alice had never been born. Now that Alice does exist, the axiological ordering will be increasing with respect to her lifetime utility, which in turn is typically an increasing function of her lifespan.
Donaldson and Weymark (1980), Ebert (1988), and Bossert (1990) allow population size to vary, and impose consistency conditions between evaluations for different populations sizes. But they do not discuss population ethics; all comparisons in these papers involve two social outcomes with the same population, rather than two social outcomes with different populations.
As noted in footnote 1, this terminology is somewhat misleading. But I use it because it is standard.
In other words, \(\phi ^+_n(r)=r\) for all \(r\in {\mathbb {R}}_+\) and \(\phi ^-_n(r)=r\) for all \(r\in {\mathbb {R}}_-\). I will often use the notation “±” in this way to simultaneously make two assertions: one in which all uses of “±” in a particular statement become “\(+\)”, and the other in which all uses of “±” in that statement become “−”.
Throughout this document, the notation “\([1\ldots N]\)” refers to the set \(\{1,\ldots ,N\}\). Likewise, “\([N\ldots {\infty })\)” refers to the set \(\{N, N+1,\ldots \}\).
See just formula (3C) for the definition of critical-level utilitarianism.
See Sect. 4 for further discussion of the Existence independence axiom.
To see this, let \(({\mathbf {x}}^+,{\mathbf {x}}^-)\in {\mathbb {R}}_{+}^{\propto _\downarrow }\times {\mathbb {R}}_{-}^{\propto _\uparrow }\). Then \({\mathbf {x}}^+\in {\mathbb {R}}_{+}^{P_\downarrow }\) and \({\mathbf {x}}^-\in {\mathbb {R}}_{-}^{N_\uparrow }\) for some \(P,N\in {\mathbb {N}}\). Let \(M:=\max \{P,N\}\); then, \({\mathbb {R}}_{+}^{P_\downarrow }\subseteq {\mathbb {R}}_{+}^{M_\downarrow }\) and \({\mathbb {R}}_{-}^{N_\uparrow }\subseteq {\mathbb {R}}_{-}^{M_\uparrow }\), so that \(({\mathbf {x}}^+,{\mathbf {x}}^-)\in {\mathbb {R}}_{+}^{M_\downarrow }\times {\mathbb {R}}_{-}^{M_\uparrow }\).
Here, \({\mathbf {x}}^\pm _{{\mathcal {J}}_\pm }=(x^\pm _j)_{j\in {\mathcal {J}}_\pm }\), an element of \({\mathbb {R}}^{{\mathcal {J}}_\pm }\). Strictly speaking, the order \(\succeq _{{\mathcal {J}}_\pm }\) need only be defined on \({\mathbb {R}}_{+}^{{\mathcal {J}}^+_\downarrow }\times {\mathbb {R}}_{-}^{{\mathcal {J}}^-_\uparrow }\). But it makes no difference if we suppose it is defined on all of \({\mathbb {R}}^{{\mathcal {J}}_+}\times {\mathbb {R}}^{{\mathcal {J}}_-}\).
Asheim and Zuber’s axioms are also stronger in that they compare populations of different sizes. Also similar are the axioms HIGAP and LIGAP, used by Bossert (1990) to characterize single-series Gini SWOs.
Technically, this “lottery” interpretation goes beyond the formal framework of the rest of the paper, which involves no risk. But in reality, social decisions always involve risk. I have confined the analysis to riskless decisions only for simplicity. We could explicitly model risk using social lotteries, and then, No Saint Petersburg Paradox could be stated directly in terms of such lotteries. But this would also raise many other issues that are beyond the scope of this paper; see, for example, Mongin and Pivato (2015, 2016, 2018).
Similarly, Roemer (2004) proposed an axiom he called Triage, which treats individuals differently depending on whether their utility is above or below a threshold corresponding to a “barely mediocre” life. But Roemer was not concerned with population ethics; rather, he was concerned with reconciling conflicting intuitions about distributional ethics which apply at different levels of utility.
There is a risk of terminological confusion here: “moral actualism” has also been used to refer to the philosophical claim that ethical judgements should be based only on the interests of the people who actually exist. See Hare (2007) for a refutation of this position. This is not what I mean by the term.
Here we adopt the notational convention that \(x^\uparrow _{0}:=-{\infty }\) and \(x^\uparrow _{N+1}={\infty }\).
Note that “\(b_{(n)}{\mathbf {x}}\)” is not well defined unless \(x^\uparrow _{n-1}\leqslant b\leqslant x^\uparrow _{n+1}\).
This is like Separability in Sect. 2.2, but in the case when \({\mathcal {J}}_\pm \) is the complement of a single coordinate.
Fleurbaey and Tungodden are not concerned with population ethics, so they only consider social welfare orders that compare social outcomes having the same population. I have reformulated their axioms in the notation of this paper.
Asheim and Zuber’s versions of Top- and Bottom-independence are called Existence independence of the best off and Existence independence of the worst off; they allow \({\mathbf {x}}\) and \({\mathbf {y}}\) to have different populations.
Alternately, instead of imposing a universal zero critical level directly through an axiom, we could derive it as a consequence of Continuity and the conjunction of two other axioms, namely Positive expansion and Negative expansion. This shows that these two axioms are also stronger than they look.
See section 4 of Thomas (2019) for further discussion of these arguments.
This also raises the question of whether we should include proto-human species such as Homo neanderthalensis or Homo heidelbergensis in the scope of the SWO. This is a deep and fascinating philosophical problem. But by the same token, it creates even more difficulties for SWOs which violate Independence of the wretched.
For another rank-dependent approach to population ethics with uncertainty, see Asheim and Zuber (2016).
This is reminiscent of Fleurbaey and Tungodden ’s (2010) tyranny of nonaggregation, but it is not the same thing. Indeed, Proposition 3.4(a) showed that any ARA (including any ARWGU) satisfies Minimal Aggregation and hence avoids the tyranny of nonaggregation. But the tyranny of nonaggregation involves a fixed population, whereas the paradox presented here depends on a variable population.
This illustrates that ARAs are not replication-invariant, as already noted in Sect. 3.3.
Actually our definition is slightly stronger than that of Chateauneuf and Wakker (1993). But it is sufficient for our purposes.
Here, I assume that the ordering of a, b versus c, d versus e, f is the same as the ordering of n, m and \(\ell \). For example, if \(n<m<\ell \), then \(a,b<c,d<e,f\).
That is: \(x^\uparrow _{n-1}\leqslant b\leqslant x^\uparrow _{n+1}\) and \(x^\uparrow _{m-1}\leqslant d\leqslant x^\uparrow _{m+1}\).
References
Adler, M.D.: Future generations: a prioritarian view. George Wash. Law Rev. 77, 1478–1520 (2008)
Adler, M.D.: Claims across outcomes and population ethics. In: Arrhenius and Bykvist (2019)
Arrhenius, G.: An impossibility theorem for welfarist axiologies. Econ. Philos. 16(2), 247–266 (2000)
Arrhenius, G.: Population Ethics. Oxford University Press, Oxford (2018)
Arrhenius, G., Bykvist, K. (eds.): The Oxford Handbook of Population Ethics. Oxford University Press, Oxford (2019). (forthcoming)
Arrhenius, G., Rabinowicz, W.: Better to be than not to be? In: Joas, H. (ed.) Benefit of Broad Horizons: Intellectual and Institutional Preconditions for a Global Social Science, pp. 399–421. Leiden, Brill (2010)
Arrhenius, G., Rabinowicz, W.: The value of existence. In: Hirose, I., Olson, J. (eds.) The Oxford Handbook of Value Theory, pp. 424–43. Oxford University Press, Oxford (2015)
Arrhenius, G., Ryberg, J., Tännsjö, T.: The repugnant conclusion. In: Zalta, E.N. (ed.) The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University (2019)
Asheim, G.B., Zuber, S.: Escaping the repugnant conclusion: rank-discounted utilitarianism with variable population. Theor. Econ. 9(3), 629–650 (2014)
Asheim, G.B., Zuber, S.: Evaluating intergenerational risks. J. Math. Econ. 65, 104–117 (2016)
Asheim, G., Zuber, S.: Rank-discounting as a resolution to a dilemma in population ethics. (2017)(preprint)
Balasubramanian, A.: On weighted utilitarianism and an application. Soc. Choice Welf. 44(4), 745–763 (2015)
Bernoulli, D.: Exposition of a new theory on the measurement of risk. Econometrica 22(1), 23–36. (Translated by Louise Sommer. Original title: Specimen Theoriae Novae de Mensura Sortis, 1738 (1954))
Blackorby, C., Donaldson, D.: Ratio-scale and translation-scale full interpersonal comparability without domain restrictions: admissible social-evaluation functions. Int. Econ. Rev. 23(2), 249–268 (1982)
Blackorby, C., Bossert, W., Donaldson, D.: Population ethics and the existence of value functions. J. Public Econ. 82(2), 301–308 (2001)
Blackorby, C., Bossert, W., Donaldson, D.J.: Population Issues in Social Choice Theory, Welfare Economics, and Ethics. Cambridge University Press, Cambridge (2005)
Bleichrodt, H., Rohde, K.I., Wakker, P.P.: Combining additive representations on subsets into an overall representation. J. Math. Psychol. 52(5), 304–310 (2008)
Bossert, W.: An axiomatization of the single-series Ginis. J. Econ. Theory 50(1), 82–92 (1990)
Chateauneuf, A., Wakker, P.: From local to global additive representation. J. Math. Econ. 22, 523–545 (1993)
Cowen, T.: Resolving the repugnant conclusion. In: Ryberg and Tännsjö, pp. 81–98 (2004)
Debreu, G.: Representation of a preference ordering by a numerical function. In: Thrall, R., Coombs, C., Davis, R. (eds.) Decision Processes, pp. 159–165. Wiley, New York (1954)
Debreu, G.: Topological methods in cardinal utility theory. In: Arrow, K.J., Karlin, S., Suppes, P. (eds.) Mathematical Methods in the Social Sciences 1959, pp. 16–26. Stanford University Press, Stanford (1960)
Donaldson, D., Weymark, J.A.: A single-parameter generalization of the Gini indices of inequality. J. Econ. Theory 22(1), 67–86 (1980)
Ebert, U.: Measurement of inequality: an attempt at unification and generalization. Soc. Choice Welf. 5, 147–169 (1988)
Fleurbaey, M., Tungodden, B.: The tyranny of non-aggregation versus the tyranny of aggregation in social choices: a real dilemma. Econ. Theory 44(3), 399–414 (2010)
Fleurbaey, M., Voorhoeve, A.: On the social and personal value of existence. In: Hirose, I., Reisner, A. (eds.) Weighing and Reasoning: Themes from the Philosophy of John Broome, pp. 95–109. Oxford University Press, Oxford (2015)
Greaves, H.: Population axiology. Philos. Compass 12(11), e12442 (2017)
Hare, C.: Voices from another world: must we respect the interests of people who do not, and will never, exist? Ethics 117(3), 498–523 (2007)
Holtug, N.: On the value of coming into existence. J. Ethics 5(4), 361–384 (2001)
McMahan, J.: Problems of population theory. Ethics 92(1), 96–127 (1981)
McMahan, J.: Asymmetries in the morality of causing people to exist. In: Roberts, M.A., Wasserman, D.T. (eds.) Harming Future Persons, pp. 49–68. Springer, Dordrecht (2009)
Mongin, P., Pivato, M.: Ranking multidimensional alternatives and uncertain prospects. J. Econ. Theory 157, 146–171 (2015)
Mongin, P., Pivato, M.: Social evaluation under risk and uncertainty. In: Adler, M.D., Fleurbaey, M. (Eds.) Handbook of Well-being and Public Policy, Ch. 24, pp. 711–745. Oxford University Press, Oxford (2016)
Mongin, P., Pivato, M.: Social preference under twofold uncertainty (2018) (preprint)
Nozick, R.: Anarchy, State, and Utopia. Basic Books, New York (1974)
Parfit, D.: Reasons and Persons. Oxford University Press, Oxford (1984)
Roberts, M.A.: Can it ever be better never to have existed at all? Person-based consequentialism and a new repugnant conclusion. J. Appl. Philos. 20(2), 159–185 (2003)
Roberts, M.A.: The asymmetry: a solution. Theoria 77(4), 333–367 (2011)
Roberts, M.A.: The nonidentity problem. In: Zalta, E.N. (ed.) The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University (2019)
Roemer, J.E.: Eclectic distributional ethics. Polit. Philos. Econ. 3(3), 267–281 (2004)
Ryberg, J., Tännsjö, T. (eds.): The Repugnant Conclusion: Essays on Population Ethics. Springer, New York (2004)
Sider, T.R.: Might theory X be a theory of diminishing marginal value? Analysis 51(4), 265–271 (1991)
Thomas, T.: Separability. In: Arrhenius and Bykvist (2019) (to appear)
Wakker, P.: The algebraic versus the topological approach to additive representations. J. Math. Psych. 32(4), 421–435 (1988)
Wakker, P.: Additive representations on rank-ordered sets. II. The topological approach. J. Math. Econ. 22, 1–26 (1993)
Weymark, J.A.: Generalized Gini inequality indices. Math. Soc. Sci. 1(4), 409–430 (1981)
Yaari, M.E.: A controversial proposal concerning inequality measurement. J. Econ. Theory 44(2), 381–397 (1988)
Zank, H.: Social welfare functions with a reference income. Soc. Choice Welf. 28(4), 609–636 (2007)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
I thank the participants of the 8th Murat Sertel Workshop (Caen), the Workshop on population, ethics and economic policy (Paris), and the conferences Public Economic Theory 2018 (Huẽ), Social Choice and Welfare 2018 (Seoul) and the Karlsruhe Institute of Technology for their comments. I am particularly grateful to Matt Adler, Geir Asheim, Marc Fleurbaey, Hendrik Rommeswinkel, Colin Rowat, Dean Spears, John Weymark, and Stéphane Zuber for their suggestions. Finally, I thank two referees for many constructive suggestions. This research was supported by Labex MME-DII (ANR11-LBX-0023-01) and CHOp (ANR-17-CE26-0003).
Appendices
Appendix: Proofs from Section 2
Proof of Theorem 1
The proof of “\({\Longleftarrow }\)” is straightforward, so I will focus on the proof of “\(\Longrightarrow \)”. First I will show that each of the orders \(\succeq _N\) admits an additive representation on \({\mathbb {R}}_{+}^{N_\downarrow }\times {\mathbb {R}}_{-}^{N_\uparrow }\). Then I will combine all these representations together to obtain a rank-additive SWF on \({\mathbb {R}}_{+}^{\propto _\downarrow }\times {\mathbb {R}}_{-}^{\propto _\uparrow }\). To achieve the first of these steps, I will combine the classic representation theorem of Debreu (1960) with a well-known result of Chateauneuf and Wakker (1993) (see Claim 6). But the deployment of this result requires some technical preliminaries; this is the role of Claims 1–5.
For any \(N\in {\mathbb {N}}\), let \({\mathbb {R}}_{\scriptscriptstyle ++}^{N_{\downarrow \downarrow }}:=\{{\mathbf {x}}\in {\mathbb {R}}^N\); \(x_1>x_2>\cdots>x_N>0\}\) and \({\mathbb {R}}_{\scriptscriptstyle --}^{N_{\uparrow \uparrow }}:=\{{\mathbf {x}}\in {\mathbb {R}}^N\); \(x_1<x_2<\cdots<x_N<0\}\). Clearly, \({\mathbb {R}}_{\scriptscriptstyle ++}^{N_{\downarrow \downarrow }}\) is the topological interior of \({\mathbb {R}}_{+}^{N_\downarrow }\) as a subset of \({\mathbb {R}}^N\), while \({\mathbb {R}}_{\scriptscriptstyle --}^{N_{\uparrow \uparrow }}\) is the topological interior of \({\mathbb {R}}_{-}^{N_\uparrow }\). Thus, \({\mathbb {R}}_{\scriptscriptstyle ++}^{N_{\downarrow \downarrow }}\times {\mathbb {R}}_{\scriptscriptstyle --}^{N_{\uparrow \uparrow }}\) is the interior of \({\mathbb {R}}_{+}^{N_\downarrow }\times {\mathbb {R}}_{-}^{N_\uparrow }\) in \({\mathbb {R}}^{2N}\).
Claim 1
Let \(N\in {\mathbb {N}}\). Every indifference set of \(\succeq _N\) in \({\mathbb {R}}_{\scriptscriptstyle ++}^{N_{\downarrow \downarrow }}\times {\mathbb {R}}_{\scriptscriptstyle --}^{N_{\uparrow \uparrow }}\) is connected.
Before proving Claim 1, we must develop some machinery. For any \(N\in {\mathbb {N}}\) and any \({\mathbf {r}}=(r_1,\ldots ,r_N)\in {\mathbb {R}}^N\), let \(\Vert {\mathbf {r}}\Vert :=\sqrt{r_1^2+\cdots +r_N^2}\) be its Euclidean norm. For any \({\mathbf {x}}=({\mathbf {x}}^+,{\mathbf {x}}^-)\) in \( {\mathbb {R}}_{\scriptscriptstyle ++}^{N_{\downarrow \downarrow }}\times {\mathbb {R}}_{\scriptscriptstyle --}^{N_{\uparrow \uparrow }}\), define

(This is always well defined because \(\Vert {\mathbf {x}}^-\Vert \ne 0\) for all \({\mathbf {x}}\in {\mathbb {R}}_{\scriptscriptstyle --}^{N_{\uparrow \uparrow }}\)). As the notation suggests, this will be like a sort of “pseudo-norm” on \( {\mathbb {R}}_{\scriptscriptstyle ++}^{N_{\downarrow \downarrow }}\times {\mathbb {R}}_{\scriptscriptstyle --}^{N_{\uparrow \uparrow }}\) (even though it is not a norm). For any \(r\in {\mathbb {R}}_{++}\) and \({\mathbf {x}}\in {\mathbb {R}}_{\scriptscriptstyle ++}^{N_{\downarrow \downarrow }}\times {\mathbb {R}}_{\scriptscriptstyle --}^{N_{\uparrow \uparrow }}\), we define \(r\,\star \, {\mathbf {x}}:= (r\, {\mathbf {x}}^+, \frac{1}{r} {\mathbf {x}}^-)\). It is easily verified that  . Let
. Let  ; this plays the role of the “unit sphere” for this “norm”. For any \({\mathbf {x}}\in {\mathbb {R}}_{\scriptscriptstyle ++}^{N_{\downarrow \downarrow }}\times {\mathbb {R}}_{\scriptscriptstyle --}^{N_{\uparrow \uparrow }}\), if
; this plays the role of the “unit sphere” for this “norm”. For any \({\mathbf {x}}\in {\mathbb {R}}_{\scriptscriptstyle ++}^{N_{\downarrow \downarrow }}\times {\mathbb {R}}_{\scriptscriptstyle --}^{N_{\uparrow \uparrow }}\), if  , then \(\frac{1}{r}\,\star \,{\mathbf {x}}\in {\mathcal {S}}^N\).
, then \(\frac{1}{r}\,\star \,{\mathbf {x}}\in {\mathcal {S}}^N\).
Claim 2
Let \(N\in {\mathbb {N}}\), and let \({\mathbf {x}}\in {\mathbb {R}}_{\scriptscriptstyle ++}^{N_{\downarrow \downarrow }}\times {\mathbb {R}}_{\scriptscriptstyle --}^{N_{\uparrow \uparrow }}\). Let \({\mathcal {Z}}:=\{{\mathbf {z}}\in {\mathbb {R}}_{\scriptscriptstyle ++}^{N_{\downarrow \downarrow }}\times {\mathbb {R}}_{\scriptscriptstyle --}^{N_{\uparrow \uparrow }}\); \({\mathbf {z}}\approx _N {\mathbf {x}}\}\) be the indifference set of \({\mathbf {x}}\). For any \({\mathbf {s}}\in {\mathcal {S}}^N\), there is a unique \(r\in {\mathbb {R}}_{++}\) with \(r\,\star \,{\mathbf {s}}\in {\mathcal {Z}}\). Let \(\phi ({\mathbf {s}}):=r\,\star \,{\mathbf {s}}\); this defines a continuous surjection \(\phi :{\mathcal {S}}^N{{\longrightarrow }}{\mathcal {Z}}\).
Proof
Existence and uniqueness Since \({\mathbb {R}}_{+}^{N_\downarrow }\times {\mathbb {R}}_{-}^{N_\uparrow }\) is a connected, separable topological space, and \(\succeq _N\) satisfies Continuity, the theorem of Debreu (1954) yields a continuous function \(w:{\mathbb {R}}_{+}^{N_\downarrow }\times {\mathbb {R}}_{-}^{N_\uparrow }{{\longrightarrow }}{\mathbb {R}}\) that represents \(\succeq _N\)—i.e. for all \(({\mathbf {a}}^+,{\mathbf {a}}^-),({\mathbf {b}}^+,{\mathbf {b}}^-)\in {\mathbb {R}}_{+}^{N_\downarrow }\times {\mathbb {R}}_{-}^{N_\uparrow }\), we have \(({\mathbf {a}}^+,{\mathbf {a}}^-)\succeq ({\mathbf {b}}^+,{\mathbf {b}}^-)\) if and only if \(w({\mathbf {a}}^+,{\mathbf {a}}^-)\geqslant w({\mathbf {b}}^+,{\mathbf {b}}^-)\). Furthermore, w is increasing in every coordinate, because \(\succeq _N\) satisfies Pareto.
Fix \({\mathbf {s}}\in {\mathcal {S}}\). For any \(r\in {\mathbb {R}}_{++}\), let \(v(r):=w(r\,\star \,{\mathbf {s}})\). Then \(v:{\mathbb {R}}_{++}{{\longrightarrow }}{\mathbb {R}}\) is clearly a continuous function. Suppose r is large enough that every coordinate of \(r{\mathbf {s}}^+\) is larger than the corresponding coordinate of \({\mathbf {x}}^+\), while every coordinate of \(\frac{1}{r}{\mathbf {s}}^-\) is smaller in magnitude than the corresponding coordinate of \({\mathbf {x}}^-\). Then \(r\,\star \,{\mathbf {s}}\succ {\mathbf {x}}\) by Pareto, and thus, \(v(r)=w(r\,\star \,{\mathbf {s}})>w({\mathbf {x}})\).
On the other hand, suppose r is small enough that every coordinate of \(r{\mathbf {s}}^+\) is less than the corresponding coordinate of \({\mathbf {x}}^+\), while every coordinate of \(\frac{1}{r}{\mathbf {s}}^-\) is larger in magnitude than the corresponding coordinate of \({\mathbf {x}}^-\). Then \(r\,\star \,{\mathbf {s}}\prec {\mathbf {x}}\) by Pareto, and thus, \(v(r)=w(r\,\star \,{\mathbf {s}})<w({\mathbf {x}})\).
Since w is continuous, the intermediate value theorem yields some \(r\in {\mathbb {R}}_{++}\) such that \(v(r)=w({\mathbf {x}})\)—in other words, \(w(r\,\star \,{\mathbf {s}})=w({\mathbf {x}})\), and hence \(r\,\star \,{\mathbf {s}}\approx _N{\mathbf {x}}\). Thus, \(r\,\star \,{\mathbf {s}}\in {\mathcal {Z}}\), as desired. This proves that such a r exists. The fact that it is unique follows from the Pareto axiom. This argument works for all \({\mathbf {s}}\in {\mathcal {S}}\).
Surjective Given \({\mathbf {z}}\in {\mathcal {Z}}\), let
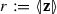 and let \({\mathbf {s}}:=\frac{1}{r}\,\star \,{\mathbf {z}}\); then, \({\mathbf {s}}\in {\mathcal {S}}^N\). But \(r\,\star \,{\mathbf {s}}={\mathbf {z}}\). Thus, \(r\,\star \,{\mathbf {s}}\in {\mathcal {Z}}\), so \(\phi ({\mathbf {s}})=r\,\star \,{\mathbf {s}}={\mathbf {z}}\).
and let \({\mathbf {s}}:=\frac{1}{r}\,\star \,{\mathbf {z}}\); then, \({\mathbf {s}}\in {\mathcal {S}}^N\). But \(r\,\star \,{\mathbf {s}}={\mathbf {z}}\). Thus, \(r\,\star \,{\mathbf {s}}\in {\mathcal {Z}}\), so \(\phi ({\mathbf {s}})=r\,\star \,{\mathbf {s}}={\mathbf {z}}\).Continuity For any \({\mathbf {s}}\in {\mathcal {S}}\) and \(\delta >0\), let \({\mathcal {B}}({\mathbf {s}},\delta ):=\{{\mathbf {b}}\in {\mathcal {S}}^N\); \(\Vert {\mathbf {b}}-{\mathbf {s}}\Vert <\delta \}\). For any \(\epsilon >0\), we will find a \(\delta >0\) such that \(\Vert \phi ({\mathbf {b}})-\phi ({\mathbf {s}})\Vert <\epsilon \) for all \({\mathbf {b}}\in {\mathcal {B}}({\mathbf {s}},\delta )\).
Suppose that \(\phi ({\mathbf {s}})=r_0\,\star \,{\mathbf {s}}\) for some \(r_0\in {\mathbb {R}}_{++}\). For any \({\mathbf {b}}=({\mathbf {b}}^+,{\mathbf {b}}^-)\in {\mathcal {S}}^N\), define
If \(r>{\overline{R}}({\mathbf {b}})\), then \(r\,b_n^+>r_0\,s^+_n\) and \(\frac{1}{r}\,b_n^->\frac{1}{r_0}\,s^-_n\) for all \(n\in [1\ldots N]\); thus, \(r\,\star \,{\mathbf {b}}=(r\,{\mathbf {b}}^+,\frac{1}{r}{\mathbf {b}}^-)\succ (r_0\,{\mathbf {s}}^+,\frac{1}{r_0}{\mathbf {s}}^-)=\phi ({\mathbf {s}})\approx {\mathbf {z}}\), so that \(r\,\star \,{\mathbf {b}}\not \in {\mathcal {Z}}\). (Here, the “\(\succ \)” is by Pareto.) Likewise, define
If \(r<{\underline{R}}({\mathbf {b}})\), then \(r\,b_n^+<r_0\,s^+_n\) and \(\frac{1}{r}\,b_n^-<\frac{1}{r_0}\,s^-_n\) for all \(n\in [1\ldots N]\); thus, \(r\,\star \,{\mathbf {b}}=(r\,{\mathbf {b}}^+,\frac{1}{r}{\mathbf {b}}^-)\prec (r_0\,{\mathbf {s}}^+,\frac{1}{r_0}{\mathbf {s}}^-)=\phi ({\mathbf {s}})\approx {\mathbf {z}}\), so that \(r\,\star \,{\mathbf {b}}\not \in {\mathcal {Z}}\). (Again, the “\(\prec \)” is by Pareto.) Thus,
Let \({\overline{\delta }}:=\min \{|s^\pm _n|\}_{n=1}^N\). For \(\delta \in (0,{\overline{\delta }})\), define
(Note: \(\delta <{\overline{\delta }}\), so \(s^+_n-\delta >0\) and \(s^-_n+\delta <0\) for all \(n\in [1\ldots N]\).) Then
Furthermore, note that
Let \(M:=\Vert {\mathbf {s}}\Vert +1\). Then
Given any \(\epsilon >0\), let \(\eta >0\) be small enough that
By statement (A3), there exists some \(\delta _1\in (0,{\overline{\delta }})\) such that
Meanwhile, let
Finally, define \(\delta :=\min \{1,\delta _1,\delta _2\}\). Now, let \({\mathbf {b}}\in {\mathcal {B}}({\mathbf {s}},\delta )\), and suppose \(\phi ({\mathbf {b}})= r\,\star \,{\mathbf {b}}\) for some \(r\in {\mathbb {R}}_{++}\). Then
as desired. Here, (a) is because \(\Vert {\mathbf {b}}^+-{\mathbf {s}}^+\Vert <\delta \) and \(\Vert {\mathbf {b}}^- - {\mathbf {s}}^-\Vert <\delta \) because \({\mathbf {b}}\in {\mathcal {B}}({\mathbf {s}},\delta )\), while \(\Vert {\mathbf {b}}^\pm \Vert \leqslant M\), by inequality (A4), because \(\delta \leqslant 1\). Next, (b) is because \(r\in (r_0-\eta ,r_0+\eta )\) by statements (A1), (A2), and (A6), because \({\mathbf {b}}\in {\mathcal {B}}({\mathbf {s}},\delta )\) and \(\delta \leqslant \delta _1\). Meanwhile, (c) is because \(\delta \leqslant \delta _2\). Finally, (d) is by definitions (A5) and (A7). \(\diamond \) Claim 2
Claim 3
For any \(N\in {\mathbb {N}}\), \({\mathcal {S}}^N\) is path-connected.
Proof
For any \(r\in (0,1)\), let
Then it is easily verified that
Now let \({\mathbf {p}}=({\mathbf {p}}^+,{\mathbf {p}}^-)\) and \({\mathbf {r}}=({\mathbf {r}}^+,{\mathbf {r}}^-)\) be two elements of \({\mathcal {S}}^N\). Let \(p_+:=\Vert {\mathbf {p}}^+\Vert \) and \(r_+:=\Vert {\mathbf {r}}^+\Vert \), and let \(p_-:=1/\sqrt{1-p_+^2}\) and \(r_-:=1/\sqrt{1-r_+^2}\). Then equation (A8) implies that \({\mathbf {p}}\in {\mathcal {S}}^N_+(p_+)\times {\mathcal {S}}^N_-(p_-)\) and \({\mathbf {r}}\in {\mathcal {S}}^N_+(r_+)\times {\mathcal {S}}^N_-(r_-)\). Now, define
Then \({\mathbf {q}}^+\in {\mathbb {R}}_{\scriptscriptstyle ++}^{\propto _{\downarrow \downarrow }}\) and \({\mathbf {q}}^-\in {\mathbb {R}}_{\scriptscriptstyle --}^{\propto _{\uparrow \uparrow }}\) (because \({\mathbf {r}}^+\in {\mathbb {R}}_{\scriptscriptstyle ++}^{\propto _{\downarrow \downarrow }}\) and \({\mathbf {r}}^-\in {\mathbb {R}}_{\scriptscriptstyle --}^{\propto _{\uparrow \uparrow }}\)) and \(\Vert {\mathbf {q}}^+\Vert =p_+\) and \(\Vert {\mathbf {q}}^-\Vert =p_-\). Thus, if \({\mathbf {q}}:=({\mathbf {q}}^+,{\mathbf {q}}^-)\) then \({\mathbf {q}}\in {\mathcal {S}}^N_+(p_+)\times {\mathcal {S}}^N_-(p_-)\); hence, \({\mathbf {q}}\in {\mathcal {S}}^N\).
Now \({\mathcal {S}}^N_+(p_+)\) is path-connected, since it is the intersection of the convex cone \({\mathbb {R}}_{\scriptscriptstyle ++}^{\propto _{\downarrow \downarrow }}\) with the radius-\(p_+\) sphere around 0 in \({\mathbb {R}}^N\). Likewise, \({\mathcal {S}}^N_-(p_-)\) is path-connected. Thus, the Cartesian product \({\mathcal {S}}^N_+(p_+)\times {\mathcal {S}}^N_-(p_-)\) is also path-connected. Thus, there is a continuous function \(\gamma :[-1,0]{{\longrightarrow }}{\mathcal {S}}^N_+(p_+)\times {\mathcal {S}}^N_-(p_-)\) such that \(\gamma (-1)={\mathbf {p}}\) and \(\gamma (0)={\mathbf {q}}\). Next, for all \(t\in [0,1]\), let \(\rho _+(t) := t\,r_+ + (1-t)\, p_+\), and define \(\rho _-(t) := 1/\sqrt{1-\rho _+(t)^2}\). Then \(\rho ^\pm :[0,1]{{\longrightarrow }}(0,1)\) are continuous functions, with \(\rho _+(0)=p_+\) and \(\rho _-(0)=p_-\), while \(\rho _+(1)=r_+\) and \(\rho _-(1)=r_-\). Define \(\gamma :[0,1]{{\longrightarrow }}{\mathcal {S}}^N\) by
Then \(\gamma \) is a continuous function, with \(\gamma (0)={\mathbf {q}}\) and \(\gamma (1)={\mathbf {r}}\). Furthermore, \(\gamma (t)\in {\mathcal {S}}^N\) for all \(t\in [0,1]\) by equation (A8).
At this point, we have constructed a continuous function \(\gamma :[-1,1]{{\longrightarrow }}{\mathcal {S}}^N\) such that \(\gamma (-1)={\mathbf {p}}\) and \(\gamma (1)={\mathbf {r}}\). This works for any \({\mathbf {p}},{\mathbf {r}}\in {\mathcal {S}}^N\). Thus, \({\mathcal {S}}^N\) is connected. \(\diamond \) Claim 3
Proof of Claim 1
Let \({\mathcal {Z}}\) be an indifference set of \(\succeq _N\) in \({\mathbb {R}}_{\scriptscriptstyle ++}^{N_{\downarrow \downarrow }}\times {\mathbb {R}}_{\scriptscriptstyle --}^{N_{\uparrow \uparrow }}\). Claim 2 says that \({\mathcal {Z}}\) is the image of \({\mathcal {S}}^N\) under a continuous function. Claims 3 says \({\mathcal {S}}^N\) is path-connected. The continuous image of a path-connected set is also connected. Thus, \({\mathcal {Z}}\) is path-connected. \(\diamond \) Claim 1
Claim 4
For every \({\mathbf {x}}\in {\mathbb {R}}_{+}^{N_\downarrow }\times {\mathbb {R}}_{-}^{N_\uparrow }\), there is some \({\mathbf {y}}\in {\mathbb {R}}_{\scriptscriptstyle ++}^{N_{\downarrow \downarrow }}\times {\mathbb {R}}_{\scriptscriptstyle --}^{N_{\uparrow \uparrow }}\) such that \({\mathbf {x}}\approx _N {\mathbf {y}}\).
Proof
As explained at the start of the proof of Claim 2, there is a continuous function \(w:{\mathbb {R}}_{+}^{N_\downarrow }\times {\mathbb {R}}_{-}^{N_\uparrow }{{\longrightarrow }}{\mathbb {R}}\) that is increasing in every coordinate and that represents \(\succeq _N\). Suppose \({\mathbf {x}}=({\mathbf {x}}^+,{\mathbf {x}}^-)\). Let \({\mathbf {z}}^+\in {\mathbb {R}}_{\scriptscriptstyle ++}^{N_{\downarrow \downarrow }}\) be obtained by increasing all coordinates of \({\mathbf {x}}^+\) slightly, so that \(z^+_1>z^+_2>\cdots>z^+_N>0\). Thus, \(w({\mathbf {z}}^+,{\mathbf {x}}^-)>w({\mathbf {x}})\), by Pareto. Let \({\mathbf {z}}^-\in {\mathbb {R}}_{-}^{N_\uparrow }\) be obtained by decreasing all coordinates of \({\mathbf {x}}^-\) slightly, so that \(z^-_1<z^-_2<\cdots<z^-_N<0\). Thus, \(w({\mathbf {x}}^+,{\mathbf {z}}^-)<w({\mathbf {x}})\), by Pareto. Now, for all \(r\in [0,1]\), let \({\mathbf {y}}^+(r):=r\,{\mathbf {z}}^+ +(1-r)\,{\mathbf {x}}^+\) and let \({\mathbf {y}}^-(r):=r\,{\mathbf {x}}^- + (1-r)\,{\mathbf {z}}^-\), and let \({\mathbf {y}}(r):=({\mathbf {y}}^+(r),{\mathbf {y}}^-(r))\). Thus, \({\mathbf {y}}(0)=({\mathbf {x}}^+,{\mathbf {z}}^-)\) and \({\mathbf {y}}(1)=({\mathbf {z}}^+,{\mathbf {x}}^-)\). It is easily verified that \({\mathbf {y}}^+(r)\in {\mathbb {R}}_{\scriptscriptstyle ++}^{N_{\downarrow \downarrow }}\) for all \(r\in (0,1]\), and \({\mathbf {y}}^-(r)\in {\mathbb {R}}_{\scriptscriptstyle --}^{N_{\uparrow \uparrow }}\) for all \(r\in [0,1)\); thus, \({\mathbf {y}}(r)\in {\mathbb {R}}_{\scriptscriptstyle ++}^{N_{\downarrow \downarrow }}\times {\mathbb {R}}_{\scriptscriptstyle --}^{N_{\uparrow \uparrow }}\) for all \(r\in (0,1)\). Now, \(w[{\mathbf {y}}(0)] = w({\mathbf {x}}^+,{\mathbf {z}}^-)< w({\mathbf {x}}) < w({\mathbf {z}}^+,{\mathbf {x}}^-) = w[{\mathbf {y}}(1)]\), and the function \(r\mapsto w[{\mathbf {y}}(r)]\) is clearly continuous. Thus, the intermediate value theorem yields some \(r\in (0,1)\) such that \(w[{\mathbf {y}}(r)]= w({\mathbf {x}})\). In other words \({\mathbf {y}}(r)\approx _N {\mathbf {x}}\). Now set \({\mathbf {y}}:={\mathbf {y}}(r)\) to prove the claim. \(\diamond \) Claim 4
Let \({\mathbf {x}}=({\mathbf {x}}^+,{\mathbf {x}}^-)\in {\mathbb {R}}_{+}^{N_\downarrow }\times {\mathbb {R}}_{-}^{N_\uparrow }\). For all \(n\in [1\ldots N]\), say that the coordinate \(x^+_n\) is interior if there is some \({\mathbf {y}}\in {\mathbb {R}}_{\scriptscriptstyle ++}^{N_{\downarrow \downarrow }}\times {\mathbb {R}}_{\scriptscriptstyle --}^{N_{\uparrow \uparrow }}\) such that \(x^+_n=y^+_n\). (Recall that \({\mathbb {R}}_{\scriptscriptstyle ++}^{N_{\downarrow \downarrow }}\times {\mathbb {R}}_{\scriptscriptstyle --}^{N_{\uparrow \uparrow }}\) is the interior of \({\mathbb {R}}_{+}^{N_\downarrow }\times {\mathbb {R}}_{-}^{N_\uparrow }\) in \({\mathbb {R}}^{2N}\).) We likewise define the interior property for the coordinates \(x^-_1,\ldots x^-_N\). In the terminology of Chateauneuf and Wakker (1993), \({\mathbf {x}}\) is interior-matched if \({\mathbf {x}}\approx _N {\mathbf {y}}\) for some \({\mathbf {y}}\in {\mathbb {R}}_{\scriptscriptstyle ++}^{N_{\downarrow \downarrow }}\times {\mathbb {R}}_{\scriptscriptstyle --}^{N_{\uparrow \uparrow }}\) and at most one of the coordinates \(x^+_1,\ldots x^+_N,x^-_1,\ldots x^-_N\) is not interior.Footnote 27 (Observe that the first half of this condition is automatically satisfied, by Claim 4.) Next, \({\mathbf {x}}\) is second-order interior-matched if \({\mathbf {x}}\approx _N {\mathbf {y}}\) for some interior or interior-matched \({\mathbf {y}}\in {\mathbb {R}}_{+}^{N_\downarrow }\times {\mathbb {R}}_{-}^{N_\uparrow }\), and at most one of the coordinates \(x^+_1,\ldots x^+_N,x^-_1,\ldots x^-_N\) does not occur in an interior or interior-matched element. Likewise, \({\mathbf {x}}\) is third-order interior-matched if \({\mathbf {x}}\approx _N {\mathbf {y}}\) for some interior, interior-matched, or second-order interior-matched \({\mathbf {y}}\in {\mathbb {R}}_{+}^{N_\downarrow }\times {\mathbb {R}}_{-}^{N_\uparrow }\), and at most one of the coordinates \(x^+_1,\ldots x^+_N,x^-_1,\ldots x^-_N\) does not occur in an interior, interior-matched element, or second-order interior-matched element. We likewise define nth-order interior-matched for all \(n\in [1\ldots N+1]\). Finally, \({\mathbf {x}}\) is matched if it is interior or is nth-order interior-matched for some \(n\in [1\ldots N+1]\).
Claim 5
Every element of \({\mathbb {R}}_{+}^{N_\downarrow }\times {\mathbb {R}}_{-}^{N_\uparrow }\) is matched.
Proof
\({\mathbf {x}}=({\mathbf {x}}^+,{\mathbf {x}}^-)\in {\mathbb {R}}_{+}^{N_\downarrow }\times {\mathbb {R}}_{-}^{N_\uparrow }\). Claim 4 guarantees that \({\mathbf {x}}\approx _N {\mathbf {y}}\) for some \({\mathbf {y}}\in {\mathbb {R}}_{\scriptscriptstyle ++}^{N_{\downarrow \downarrow }}\times {\mathbb {R}}_{\scriptscriptstyle --}^{N_{\uparrow \uparrow }}\). It remains to check the matching condition on the coordinates.
For all \(n\in [1\ldots N]\), it is easily verified that \(x^+_n\) is interior if and only if \(x^+_n>0\). Likewise, \(x^-_n\) is interior if and only if \(x^-_n<0\). Thus, \({\mathbf {x}}\) is interior-matched if and only if at most one of the coordinates \(x^+_1,\ldots x^+_N,x^-_1,\ldots x^-_N\) is zero. It is easily seen that this occurs if and only if \(x^+_{N-1}>0\) and \(x^-_{N-1}<0\), and at least one of \(x^+_N\) and \(x^-_N\) is nonzero.
Now suppose that both \(x^+_N=0\) and \(x^-_N=0\). Then each of these two coordinates can be matched to an interior-matched point (by the previous paragraph). Thus, in this case, \({\mathbf {x}}\) is second-order interior-matched if and only if all the coordinates \(x^\pm _1,\ldots ,x^\pm _{N-2}\) are nonzero, and at least one of the coordinates \(x^+_{N-1}\) and \(x^-_{N-1}\) is nonzero.
If both \(x^+_{N-1}=0\) and \(x^-_{N-1}=0\) (and hence, \(x^+_N=0\) and \(x^-_N=0\)), then each of the two coordinates \(x^+_{N-1}\) and \(x^-_{N-1}\) can individually be matched to some second-order interior-matched point (by the previous paragraph), while each of the two coordinates \(x^+_{N}\) and \(x^-_{N}\) can individually be matched to some interior-matched point. Thus, in this case, \({\mathbf {x}}\) is third-order interior-matched if and only if all the coordinates \(x^\pm _1,\ldots ,x^\pm _{N-3}\) are nonzero, and at least one of the coordinates \(x^+_{N-2}\) and \(x^-_{N-2}\) is nonzero.
Proceeding inductively, we see that, for all \(n\in [1\ldots N]\), \({\mathbf {x}}\) is nth-order interior-matched if and only if all the coordinates \(x^\pm _1,\ldots ,x^\pm _{N-n}\) are nonzero, and at most one of the coordinates \(x^+_{N-n+1}\) and \(x^-_{N-n+1}\) is zero. In particular, \({\mathbf {x}}\) is Nth-order interior-matched if and only if at least one of \(x^+_1\) and \(x^-_1\) is nonzero—in other words, as long as \({\mathbf {x}}\) itself is not the zero vector. Thus, the zero vector itself is \((N+1)\)th-order interior-matched. Hence, every element of \({\mathbb {R}}_{+}^{N_\downarrow }\times {\mathbb {R}}_{-}^{N_\uparrow }\) is either interior or nth-order interior-matched for some \(n\in [1\ldots N+1]\) and thus matched. \(\diamond \) Claim 5
Claim 6
For all \(N\in {\mathbb {N}}\) with \(N\geqslant 3\), there exists a unique system of continuous, increasing functions \(\psi ^+_1,\ldots ,\psi ^+_N:{\mathbb {R}}_+{{\longrightarrow }}{\mathbb {R}}\) and \(\psi ^-_1,\ldots ,\psi ^-_N:{\mathbb {R}}_-{{\longrightarrow }}{\mathbb {R}}\) with \(\psi ^+_1(1)=1\) and with \(\psi ^\pm _n(0)=0\) for all \(n\in [1\ldots N]\), such that, for any \({\mathbf {x}}=({\mathbf {x}}^+,{\mathbf {x}}^-)\) and \({\mathbf {y}}=({\mathbf {y}}^+,{\mathbf {y}}^-)\) in \({\mathbb {R}}_{+}^{N_\downarrow }\times {\mathbb {R}}_{-}^{N_\uparrow }\), we have

Proof
An open box in \({\mathbb {R}}^{2N}\) is an open set of the form \((a_1,z_1)\times (a_2,z_2)\times \cdots \times (a_{2N},z_{2N})\subset {\mathbb {R}}^{2N}\), for some \(a_1<z_1\), \(a_2<z_2\), \(\ldots \), \(a_{2N}<z_{2N}\). Let \({\mathcal {B}}\subset {\mathbb {R}}_{\scriptscriptstyle ++}^{N_{\downarrow \downarrow }}\times {\mathbb {R}}_{\scriptscriptstyle --}^{N_{\uparrow \uparrow }}\) be an open box, and let \(\succeq _{\mathcal {B}}\) be the restriction of \(\succeq _N\) to an ordering on \({\mathcal {B}}\). In the terminology of Debreu (1960), \(\succeq _{\mathcal {B}}\) is continuous, separable, and increasing in every coordinate, by the axioms Continuity, Separability, and Pareto, respectively. Thus, Theorem 3 of Debreu (1960) says that \(\succeq _{\mathcal {B}}\) admits an additive representation—that is, there are continuous, increasing functions \(\psi ^{\mathcal {B}}_n:(a_n,z_n){{\longrightarrow }}{\mathbb {R}}\) for all \(n\in [1\ldots 2N]\) such that, for any \({\mathbf {b}},{\mathbf {c}}\in {\mathcal {B}}\), we have

\({\mathbb {R}}_{\scriptscriptstyle ++}^{N_{\downarrow \downarrow }}\times {\mathbb {R}}_{\scriptscriptstyle --}^{N_{\uparrow \uparrow }}\) is open, so it can be covered by such open boxes. Thus, in the terminology of Chateauneuf and Wakker (1993), the ordering \(\succeq _N\) admits “local” additive representations everywhere on \({\mathbb {R}}_{\scriptscriptstyle ++}^{N_{\downarrow \downarrow }}\times {\mathbb {R}}_{\scriptscriptstyle --}^{N_{\uparrow \uparrow }}\). Since \({\mathbb {R}}_{\scriptscriptstyle ++}^{N_{\downarrow \downarrow }}\times {\mathbb {R}}_{\scriptscriptstyle --}^{N_{\uparrow \uparrow }}\) is a convex set, it clearly satisfies conditions (1) and (2) in Structural Assumption 2.1 of Chateauneuf and Wakker (1993). Meanwhile, condition (3) of Chateauneuf and Wakker (1993) is true by Claim 1. Finally, Claim 5 says that every element of \({\mathbb {R}}_{+}^{N_\downarrow }\times {\mathbb {R}}_{-}^{N_\uparrow }\) is “matched”. Thus, by Theorem 3.3(a) of Chateauneuf and Wakker (1993), the local additive representations (A10) can be combined together to yield a single global additive representation of \(\succeq _N\) on all of \({\mathbb {R}}_{+}^{N_\downarrow }\times {\mathbb {R}}_{-}^{N_\uparrow }\). That is, there exist continuous, increasing functions \(\psi ^+_1,\ldots ,\psi ^+_N:{\mathbb {R}}_+{{\longrightarrow }}{\mathbb {R}}\) and \(\psi ^-_1,\ldots ,\psi ^-_N:{\mathbb {R}}_-{{\longrightarrow }}{\mathbb {R}}\) giving the additive representation (A9). Furthermore, the functions \(\psi ^+_1,\ldots ,\psi ^+_N,\psi ^-_1,\ldots ,\psi ^-_N\) are unique up to increasing affine transformation with a common scalar multiplication.
For all \(n\in [1\ldots N]\), let \(k^\pm _n:=\psi ^\pm _n(0)\). By replacing \(\psi ^\pm _n\) with the function \(\psi ^\pm _n-k^\pm _0\) if necessary, we can assume without loss of generality that \(\psi ^\pm _n(0)=0\) for all \(n\in [1\ldots N]\). Now let \(s:=\psi ^+_1(1)\). By replacing \(\psi ^\pm _n\) with the function \(\psi ^\pm _n/s\) for all \(n\in [1\ldots N]\) if necessary, we can assume without loss of generality that \(\psi ^+_1(1)=1\). \(\diamond \) Claim 6
For all \(N\in {\mathbb {N}}\), Claim 6 yields a collection of functions \(\psi ^+_{N,1},\ldots ,\psi ^+_{N,N}:{\mathbb {R}}_+{{\longrightarrow }}{\mathbb {R}}_+\) and \(\psi ^-_{N,1},\ldots ,\psi ^-_{N,N}:{\mathbb {R}}_-{{\longrightarrow }}{\mathbb {R}}_-\) providing an additive representation (A9) for \(\succeq _N\) on \({\mathbb {R}}_{+}^{N_\downarrow }\times {\mathbb {R}}_{-}^{N_\uparrow }\), and furthermore such that \(\psi ^+_{N,1}(1)=1\) and \(\psi ^\pm _{N,n}(0)=0\) for all \(n\in [1\ldots N]\).
Now, if \(N<M\), then \({\mathbb {R}}_{+}^{N_\downarrow }\) can be embedded into \({\mathbb {R}}_{+}^{M_\downarrow }\) in a natural way, by sending \((x_1,x_2,\ldots ,x_N)\) to \( (x_1,x_2,\ldots ,x_N,0,0,\ldots ,0)\) (where there are \(M-N\) zeros). Likewise, \({\mathbb {R}}_{-}^{N_\uparrow }\) embeds into \({\mathbb {R}}_{-}^{M_\uparrow }\) in a natural way. Thus, we obtain a natural embedding of \({\mathbb {R}}_{+}^{N_\downarrow }\times {\mathbb {R}}_{-}^{N_\uparrow }\) into \({\mathbb {R}}_{+}^{M_\downarrow }\times {\mathbb {R}}_{-}^{M_\uparrow }\). Under this embedding, the ordering \(\succeq _N\) is the restriction of the ordering \(\succeq _M\) to \({\mathbb {R}}_{+}^{N_\downarrow }\times {\mathbb {R}}_{-}^{N_\uparrow }\) (because both arise as restrictions of the order \(\succeq _*\) to their respective domains). Thus, the functions \(\psi ^+_{M,1},\ldots ,\psi ^+_{M,N},\psi ^-_{M,1},\ldots ,\psi ^-_{M,N}\) yield a second additive representation of \(\succeq _N\). But the additive representations in Claim 6 are unique. Thus, we obtain \(\psi ^\pm _{M,n}=\psi ^\pm _{N,n}\) for all \(n\in [1\ldots N]\). It follows that there is in fact a single infinite sequence of functions \((\phi ^+_n)_{n=1}^{\infty }\) such that
Likewise, there is a single infinite sequence of functions \((\phi ^-_n)_{n=1}^{\infty }\) such that
It remains to show that the functions \(\{\phi ^+_n\}_{n=1}^{\infty }\) and \(\{\phi ^-_n\}_{n=1}^{\infty }\) yield the additive representation (2B) for \(\succeq _*\). To see this, let \({\mathbf {x}},{\mathbf {y}}\in {\mathbb {R}}_{+}^{\propto _\downarrow }\times {\mathbb {R}}_{-}^{\propto _\uparrow }\). From formula (2G), there exist \(L,M\in {\mathbb {N}}\) such that \({\mathbf {x}}\in {\mathbb {R}}_{+}^{L_\downarrow }\times {\mathbb {R}}_{-}^{L_\uparrow }\), and \({\mathbf {y}}\in {\mathbb {R}}_{+}^{M_\downarrow }\times {\mathbb {R}}_{-}^{M_\uparrow }\). Let \(N:=\max \{L,M\}\). Then \({\mathbb {R}}_{+}^{L_\downarrow }\times {\mathbb {R}}_{-}^{L_\uparrow }\subseteq {\mathbb {R}}_{+}^{N_\downarrow }\times {\mathbb {R}}_{-}^{N_\uparrow }\) and \({\mathbb {R}}_{+}^{M_\downarrow }\times {\mathbb {R}}_{-}^{M_\uparrow }\subseteq {\mathbb {R}}_{+}^{N_\downarrow }\times {\mathbb {R}}_{-}^{N_\uparrow }\). Thus, both \({\mathbf {x}}\) and \({\mathbf {y}}\) are elements of \({\mathbb {R}}_{+}^{N_\downarrow }\times {\mathbb {R}}_{-}^{N_\uparrow }\), and we have

as desired. Here, (a) is by the definition of \(\succeq _N\), (b) is by the additive representation (A9), (c) is by Eqs. (A11) and (A12), and (d) is because \({\mathbf {x}},{\mathbf {y}}\in {\mathbb {R}}_{+}^{N_\downarrow }\times {\mathbb {R}}_{-}^{N_\uparrow }\), so that \(x^+_n=0\) and \(y^+_n=0\) for all \(n\in [N+1\ldots {\infty })\). \(\square \)
Remark
The proof of Claim 6 uses a very similar strategy to Ebert’s (1988) proof of his Theorem 1. But Ebert’s proof contains an error, identified by Wakker (1993, §2.3). Fortunately, the result claimed by Ebert is actually correct (Wakker 1993, Corollary 3.6). But this result only applies to the open cone of strictly positive nonincreasing vectors \({\mathbb {R}}^{N_\downarrow }_{++}\), whereas we need the corresponding result for the closed cone \({\mathbb {R}}_{+}^{N_\downarrow }\) of nonnegative nonincreasing vectors. As shown by Wakker (1993, Example 3.8), this extension does not come for free; hence, the detailed argument is provided above in the proof of Claims 1–6. Despite Wakker’s (1993) admonition, later authors have recapitulated Ebert’s error. For example, Balasubramanian (2015, Corollary 3) repeats Ebert’s proof almost verbatim. Likewise, in the proof of their Lemma 1, Asheim and Zuber (2014) cite Ebert’s (1988) Theorem 1 without correction.
Proof of Proposition 2.1
(a) Let \(\succeq _N\) be the restriction of the order \(\succeq _*\) to \({\mathbb {R}}_{+}^{N_\downarrow }\), while \(\succeq _{N+1}\) is the restriction of \(\succeq _*\) to \({\mathbb {R}}_{+}^{N+1_\downarrow }\). Let \({\mathbf {x}}=(x_1,\ldots ,x_N)\) and \({\mathbf {y}}=(y_1,\ldots ,y_N)\) be in \({\mathbb {R}}_{+}^{N_\downarrow }\), let \(z>\max (x_1,y_1)\), and let \({\mathbf {x}}':=(z,x_1,\ldots ,x_N)\) and \({\mathbf {y}}':=(z,y_1,\ldots ,y_N)\). Then \({\mathbf {x}}',{\mathbf {y}}'\in {\mathbb {R}}_{+}^{N+1_\downarrow }\), and we have

Here, \((\dagger )\) is by Top-independence in good worlds, while \((*)\) is by the representation (2B). This equivalence holds for all \({\mathbf {x}},{\mathbf {y}}\in {\mathbb {R}}_{+}^{N_\downarrow }\), and this argument can be repeated for any \(N\in {\mathbb {N}}\). Thus, if we define \(\psi ^+_n:=\phi ^+_{n+1}\) for all \(n\in {\mathbb {N}}\), then the functions \(\{\psi ^+_n\}_{n=1}^{\infty }\) and \(\{\phi ^-_n\}_{n=1}^{\infty }\) yield another rank-additive representation like (2B) for \(\succeq \). But the functions \(\{\phi ^\pm _n\}_{n=1}^{\infty }\) in this representation are unique up to multiplication by a common scalar. Thus, there is some \(\beta >0\) such that \(\psi _{n}^+ = \, \beta \,\phi _n^+\) for all \(n\in {\mathbb {N}}\)—equivalently, \(\phi _{n+1}^+ = \, \beta \,\phi _n^+\) for all \(n\in {\mathbb {N}}\). Let \(\phi ^+:=\phi ^+_1/\beta \); then, we obtain \(\phi ^+_n:=\beta ^n\,\phi ^+\) for all \(n\in {\mathbb {N}}\). The result follows.
The proof of (b) is almost identical, but works with \(\{\phi ^-_n\}_{n=1}^{\infty }\) instead of \(\{\phi ^+_n\}_{n=1}^{\infty }\). The uniqueness claims in parts (a), (b) and (c) all follow immediately from the uniqueness statement in Theorem 1. \(\square \)
Proof of Proposition 2.2
First, note that the supremum \({\overline{W}}\) is never obtained by any \({\mathbf {x}}\in {\mathcal {X}}\), even if \({\overline{W}}\) is finite. To see this, suppose by contradiction that \(W({\mathbf {x}})={\overline{W}}\) for some \({\mathbf {x}}\in {\mathcal {X}}\). Let \({\mathbf {x}}'\) be obtained by increasing \({\mathbf {x}}\) by some amount in every nonzero coordinate. Then \(W({\mathbf {x}}')>W({\mathbf {x}})\), because the functions \(\phi _n^\pm \) are all strictly increasing. Thus, \(W({\mathbf {x}}')>{\overline{W}}\), contradicting the definition of \({\overline{W}}\).
- (a)
“\(\Longrightarrow \)” Let \({\mathbf {x}}\) and \(r_0\) be as in the formulation of No Repugnant Conclusion. For any \(N\in {\mathbb {N}}\), we have \({\mathbf {x}}\succ r_0\varvec{1}_N\), and thus,
$$\begin{aligned} W({\mathbf {x}})> W(r_0\varvec{1}_N) = \sum _{n=1}^N \phi ^+_n(r_0). \end{aligned}$$Taking the limit as \(N{\rightarrow }{\infty }\), we obtain \(\displaystyle \sum \limits _{n=1}^{\infty }\phi ^+_n(r_0)\leqslant W({\mathbf {x}}) < {\overline{W}}\), as desired.
“\({\Longleftarrow }\)” Let \(r_0\) satisfy the condition in the theorem. Then there exists some \({\mathbf {x}}\in {\mathcal {X}}\) such that \(W({\mathbf {x}})> \sum _{n=1}^{\infty }\phi ^+_n(r_0)\), and thus, \(W({\mathbf {x}})> \sum _{n=1}^N \phi ^+_n(r_0)\) for all \(N\in {\mathbb {N}}\). It follows that \({\mathbf {x}}\succ r_0\varvec{1}_N\) for all \(N\in {\mathbb {N}}\), as desired.
- (b)
“\(\Longrightarrow \)” For any \(N\in {\mathbb {N}}\), let \({\mathbf {x}}\in {\mathcal {X}}\) satisfy the statement of No utility monsters. Thus, for all \(r\in {\mathbb {R}}_+\), we have \({\mathbf {x}}\succ r\,\varvec{1}_N\), and thus,
$$\begin{aligned} W({\mathbf {x}})> W(r\,\varvec{1}_N) = \sum _{n=1}^N \phi ^+_n(r). \end{aligned}$$Taking the limit as \(r{\rightarrow }{\infty }\), we obtain \(\displaystyle \lim _{r{\rightarrow }{\infty }} \sum \nolimits _{n=1}^N \phi ^+_n(r)\leqslant W({\mathbf {x}})<{\overline{W}}\), as desired.
“\({\Longleftarrow }\)” For any \(N\in {\mathbb {N}}\), we have \(\lim _{r{\rightarrow }{\infty }} \sum \nolimits _{n=1}^N \phi ^+_n(r)<{\overline{W}}\). Thus, there exists some \({\mathbf {x}}\in {\mathcal {X}}\) such that \(\lim _{r{\rightarrow }{\infty }} \sum \nolimits _{n=1}^N \phi ^+_n(r)<W({\mathbf {x}})\). Thus, for all \(r\in {\mathbb {R}}_+\), we have \(W(r\,\varvec{1}_N)<W({\mathbf {x}})\), and thus, \(r\,\varvec{1}_N\prec {\mathbf {x}}\), as desired.
For the last statement of the theorem, suppose that \({\overline{W}}<{\infty }\). Let \(r_0>0\), and let \(r_1>r_0\); then, \( \sum _{n=1}^{\infty }\phi ^+_n(r_1) \leqslant {\overline{W}}\). Now let \(\delta :=\phi ^+_1(r_1)-\phi ^+_1(r_0)\). Then \(\delta >0\) because \(\phi ^+_1\) is strictly increasing, and we have
It follows that \(\sum _{n=1}^{\infty }\phi ^+_n(r_0)<{\overline{W}}\). Thus, the condition in part (a) is satisfied. (In fact, this argument works for all\(r_0>0\).) By a similar argument, we deduce that \(\lim _{r{\rightarrow }{\infty }} \sum \nolimits _{n=1}^N \phi ^+_n(r)<{\overline{W}}\), for all \(N\in {\mathbb {N}}\). Thus, part (b) is satisfied. \(\square \)
Proof of Proposition 2.3
The first statement is obvious. The second follows immediately from Proposition 2.2. \(\square \)
Proof of Proposition 2.4
Before proceeding with the proof of (a), (b), and (c), we need some preliminary observations. Let \(\succeq \) be a SWO on \({\mathcal {X}}\). Let \(\succeq _*\) be the ordering on \({\mathbb {R}}_{+}^{\propto _\downarrow }\times {\mathbb {R}}_{-}^{\propto _\uparrow }\) defined via statement (2A).
Claim 1
\(\succeq \) satisfies Inequality neutrality (respectively, Inequality aversion, resp. Strict inequality aversion) on \({\mathcal {X}}\) if and only if \(\succeq _*\) satisfies the same axiom on \({\mathbb {R}}_{+}^{\propto _\downarrow }\times {\mathbb {R}}_{-}^{\propto _\uparrow }\).
Proof
Let \({\mathbf {x}},{\mathbf {y}}\in {\mathcal {X}}\). Say that \({\mathbf {y}}\) is a rank-preserving Pigou–Dalton transform of \({\mathbf {x}}\) if \({\mathbf {y}}\) is a Pigou–Dalton transform of \({\mathbf {x}}\), and furthermore, for all \(i,j\in {\mathcal {I}}\), if \(x_i< x_j\), then \(y_i\leqslant y_j\); also, if \(x_i< 0\), then \(y_i\leqslant 0\); finally, if \(x_i> 0\), then \(y_i\geqslant 0\). In other words, the reallocation of utility does not change the ranking of people from best-off to worst-off which we use to apply the rank-additive SWF (2B). Note that we allow the possibility that \(x_i< x_j\) but \(y_i= y_j\)—the reallocation may equalize two people (so that afterwards they could be ranked in either order). Likewise, we allow the possibility that \(x_i<0\) (or \(x_i>0\)) but \(y_i=0\). The following facts are easily verified:
- (a):
For any \({\mathbf {x}},{\mathbf {z}}\in {\mathcal {X}}\), \({\mathbf {z}}\) is an ordinary Pigou–Dalton transform of \({\mathbf {x}}\) if and only if there is a sequence \({\mathbf {x}}={\mathbf {y}}_0,{\mathbf {y}}_1,{\mathbf {y}}_2,\ldots ,{\mathbf {y}}_N={\mathbf {z}}\) such that for all \(n\in [1\ldots N]\), \({\mathbf {y}}_n\) is a rank-preserving Pigou–Dalton transform of \({\mathbf {y}}_{n-1}\).
- (b):
For any \({\mathbf {x}},{\mathbf {y}}\in {\mathcal {X}}\), if \({\mathbf {y}}\) is a rank-preserving Pigou–Dalton transform of \({\mathbf {x}}\), then \(({\mathbf {y}}^+,{\mathbf {y}}^-)\) is an ordinary Pigou–Dalton transform of \(({\mathbf {x}}^+,{\mathbf {x}}^-)\).
Fact (a) means that \(\succeq \) satisfies Inequality neutrality (resp. Inequality aversion, resp. Strict inequality aversion) with respect to rank-preserving Pigou–Dalton transforms if and only if it satisfies this axiom with respect to all Pigou–Dalton transforms. Fact (b) means that \(\succeq \) satisfies one of these three axioms with respect to rank-preserving Pigou–Dalton transforms if and only if \(\succeq _*\) satisfies the corresponding axiom (in its ordinary form) on \({\mathbb {R}}_{+}^{\propto _\downarrow }\times {\mathbb {R}}_{-}^{\propto _\uparrow }\). This proves the claim. \(\diamond \) Claim 1
Now let \({\mathbf {x}}=({\mathbf {x}}^+,{\mathbf {y}}^-)\) and \({\mathbf {y}}=({\mathbf {y}}^+,{\mathbf {y}}^-)\) be elements of \({\mathbb {R}}_{+}^{\propto _\downarrow }\times {\mathbb {R}}_{-}^{\propto _\uparrow }\), and suppose \({\mathbf {y}}\) is a Pigou–Dalton transform of \({\mathbf {x}}\). Then there exist \(m,n\in {\mathbb {N}}\) and \(\epsilon >0\) such that one of the following three cases occurs:
- (i)
\(y^-_m=x^-_m+\epsilon \leqslant 0\leqslant y^+_n=x^+_n-\epsilon \), while \(y^-_\ell =x^-_\ell \) for all \(\ell \in {\mathbb {N}}\setminus \{m\}\), and \(y^+_\ell =x^+_\ell \) for all \(\ell \in {\mathbb {N}}\setminus \{n\}\).
- (ii)
\(m>n\), and \(y^+_m=x^+_m+\epsilon \leqslant y^+_n=x^+_n-\epsilon \), while \(y^+_\ell =x^+_\ell \) for all \(\ell \in {\mathbb {N}}\setminus \{m,n\}\), and \(y^-_\ell =x^-_\ell \) for all \(\ell \in {\mathbb {N}}\).
- (iii)
\(m<n\), and \(y^-_m=x^-_m+\epsilon \leqslant y^-_n=x^-_n-\epsilon \), while \(y^-_\ell =x^-_\ell \) for all \(\ell \in {\mathbb {N}}\setminus \{m,n\}\), and \(y^+_\ell =x^+_\ell \) for all \(\ell \in {\mathbb {N}}\).
Let W be the SWF in formula (2B). The \(W({\mathbf {y}})-W({\mathbf {x}})\) takes the following form in Cases (i), (ii), and (iii):
With these preliminaries established, we proceed with the proof of parts (a), (b), and (c) of the theorem. In each of (a), (b), and (c), it is easily verified that the stated conditions are sufficient for \(\succeq _*\) to satisfy the stated axiom—and hence, for \(\succeq \) to satisfy it, by Claim 1. It remains to prove that they are also necessary.
(a) Suppose \(\succeq \) (and hence, \(\succeq _*\)) satisfies Inequality neutrality. So if \({\mathbf {y}}\) is a Pigou–Dalton transform of \({\mathbf {x}}\), then \(W({\mathbf {y}})=W({\mathbf {x}})\). Thus, for any \(m,n\in {\mathbb {N}}\), any \(\epsilon >0\), and any \(x^-_m<-\epsilon \) and \(x^+_n>\epsilon \), the right-hand side of equation (I) is zero. Thus, there is some constant \(C>0\) such that \(\phi ^-_m(x^-_m+\epsilon )-\phi ^-_m(x^-_m) =C\) and \(\phi ^+_n(x^+_n)-\phi ^+_n(x^+_n-\epsilon )=C\) for all \(x^-_m<-\epsilon \) and \(x^+_n>\epsilon \). Thus, \(\phi ^+_n\) and \(\phi ^-_m\) must each have a constant slope—in fact, the same slope. Since \(\phi ^+_n(0)=0\) and \(\phi ^-_m(0)=0\) by assumption, this means they are linear functions with the same slope. Varying this argument over all \(m,n\in {\mathbb {N}}\), we conclude that the \(\{\phi ^+_n\}_{n=1}^{\infty }\) and \(\{\phi ^-_n\}_{n=1}^{\infty }\) are all linear functions with the same slope. Thus, SWF (2B) is equivalent (up to multiplication by a scalar) to the classical utilitarian SWF (2C).
(b) Suppose \(\succeq \) (and hence, \(\succeq _*\)) satisfies Inequality aversion. So if \({\mathbf {y}}\) is a Pigou–Dalton transform of \({\mathbf {x}}\), then \(W({\mathbf {y}})\geqslant W({\mathbf {x}})\). Thus, for any \(m,n\in {\mathbb {N}}\), any \(\epsilon >0\), and any \(x^\pm _n,x^\pm _m\in {\mathbb {R}}\), we have:
− If \(x^-_m<-\epsilon \) and \(x^+_n>\epsilon \), then the right-hand side of equation (I) is nonnegative.
− If \(x^+_n-2\epsilon \geqslant x^+_m\geqslant 0\), then the right-hand side of equation (II) is nonnegative.
− If \(0\geqslant x^-_n\geqslant x^-_m+2\epsilon \), then the right-hand side of equation (III) is nonnegative.
Setting \(s:=x^\pm _m+\epsilon \) and \(r:=x^\pm _n-\epsilon \) in all three cases, we obtain inequalities (i), (ii), and (iii) in part (b) of the theorem.
To obtain inequality (2H), let \(J\in {\mathbb {N}}\), and let \(\epsilon :=q/J\). Then for any \(n<m\in {\mathbb {N}}\),
Here, \((*)\) is by inequality (b)(ii), where for each summand, we set \(r=s=j\epsilon \), so that \(r+\epsilon =(j+1)\epsilon \) and \(s-\epsilon =(j-1)\epsilon \). We have also used several times the fact that \(\phi _n^+(0)=\phi _m^+(0)=0\). Taking the limit as \(J{\rightarrow }{\infty }\), we obtain:
where the last step is because \(\phi _n^+\) is continuos at 0 and at q. Thus, we deduce that \(\phi _n^+(q)\leqslant \phi _m^+(q)\) for all \(q\in {\mathbb {R}}_+\) and \(n<m\in {\mathbb {N}}\). This justifies all the inequalities on the left side of (2H). By an almost identical argument [using inequality (b)(iii)], we deduce that \(\phi _n^-(q)\leqslant \phi _m^-(q)\) for all \(q\in {\mathbb {R}}_+\) and \(n>m\in {\mathbb {N}}\); this justifies all the inequalities on the right side of (2H). Finally, by a similar argument [using inequality (b)(i)], we deduce that \(\phi _n^+(q)\leqslant \phi _m^-(q)\) for all \(q\in {\mathbb {R}}_+\) and all \(n,m\in {\mathbb {N}}\). This justifies the inequalities between the left and right sides of (2H).
To prove inequality (2I), observe that inequalities (b)(i)–(b)(iii) imply the following
- (i)
If \(r\geqslant 0\geqslant s\), then \(\displaystyle \frac{\phi ^+_n(r+\epsilon )-\phi ^+_n(r)}{\epsilon } \leqslant \frac{\phi ^-_m(s)-\phi ^-_m(s-\epsilon )}{\epsilon }\).
- (ii)
If \(n< m\) and \(r\geqslant s\geqslant \epsilon >0\), then \(\displaystyle \frac{\phi ^+_n(r+\epsilon )-\phi ^+_n(r)}{\epsilon } \leqslant \frac{\phi ^+_m(s)-\phi ^+_m(s-\epsilon )}{\epsilon }\).
- (iii)
If \(n> m\) and \(s\leqslant r\leqslant -\epsilon <0\), then \(\displaystyle \frac{\phi ^-_n(r+\epsilon )-\phi ^-_n(r)}{\epsilon } \leqslant \frac{\phi ^-_m(s)-\phi ^-_m(s-\epsilon )}{\epsilon }\).
Taking the limit as \(\epsilon {\rightarrow }0\) in all three cases, we deduce:
- (i\('\)):
If \(r\geqslant 0\geqslant s\), then \((\phi ^+_n)'(r) \leqslant (\phi ^-_m)'(s)\).
- (ii\('\)):
If \(n< m\) and \(r\geqslant s>0\), then \((\phi ^+_n)'(r) \leqslant (\phi ^+_m)'(s)\).
- (iii\('\)):
If \(n> m\) and \(s\leqslant r<0\), then \((\phi ^-_n)'(r) \leqslant (\phi ^-_m)'(s)\).
If \(r_1\geqslant r_2 \geqslant r_3 \geqslant \cdots \geqslant 0\) and \(s_1 \leqslant s_2 \leqslant s_3 \leqslant \cdots \leqslant 0\), then each of the inequalities in between adjacent terms in (2I) can be obtained by invoking one of inequalities (i\('\)), (ii\('\)), or (iii\('\)).
- (c)
The proof is identical to (b), but with strict inequalities.
\(\square \)
Proof of Proposition 2.6
Easy modification of the proof of Proposition 2.4. \(\square \)
Appendix: Proofs from Section 3
Parts of the proof of Theorem 2 are analogous to parts of the proof of Theorem 1. When noting these analogies, I will refer to Claim N in the proof of Theorem 1 as “Claim 1.N”.
Proof of Theorem 2
The proof of “\({\Longleftarrow }\)” is straightforward, so I will focus on the proof of “\(\Longrightarrow \)”. First, Claims 1–6 will show that each of the orders \(\succeq _N\) admits an additive representation on \({\mathbb {R}}^{N_\uparrow }\). Then, Claims 7–14 will combine all these representations together to obtain an ARA SWF on \({\mathbb {R}}^{\propto _\uparrow }\).
The binary relation “\(\cong \)” in the Trade-off Consistency axiom is clearly symmetric: if \({(a{\mathop {\leadsto }\limits ^{n}} b)} \cong {(c{\mathop {\leadsto }\limits ^{m}} d)}\), then \({(c{\mathop {\leadsto }\limits ^{m}} d)} \cong {(a{\mathop {\leadsto }\limits ^{n}} b)}\). Claim 1 shows that \(\cong \) is also “transitive”.
Claim 1
Let \(n,m,\ell \in {\mathbb {N}}\) be distinct, and let \(a,b,c,d,e,f\in {\mathbb {R}}\). If \({(a{\mathop {\leadsto }\limits ^{n}} b)} \cong {(c{\mathop {\leadsto }\limits ^{m}} d)}\) and \({(c{\mathop {\leadsto }\limits ^{m}} d)} \cong {(e{\mathop {\leadsto }\limits ^{\ell }} f)}\), then \({(a{\mathop {\leadsto }\limits ^{n}} b)} \cong {(e{\mathop {\leadsto }\limits ^{\ell }} f)}\).Footnote 28
Proof
For any \({\mathbf {x}}\in {\mathcal {X}}\), if \(x^\uparrow _n=a\) and \(x^\uparrow _m=c\), and \(b_{(n)}{\mathbf {x}}\) and \(d_{(m)}{\mathbf {x}}\) are well defined,Footnote 29 then Trade-off Consistency says that
because \({(a{\mathop {\leadsto }\limits ^{n}} b)} \cong {(c{\mathop {\leadsto }\limits ^{m}} d)}\). Likewise, for any \({\mathbf {x}}\in {\mathcal {X}}\), if \(x^\uparrow _m=c\) and \(x^\uparrow _\ell =e\), and \(d_{(m)}{\mathbf {x}}\) and \(f_{(\ell )}{\mathbf {x}}\) are well defined, then Trade-off Consistency says that
because \({(c{\mathop {\leadsto }\limits ^{m}} d)} \cong {(e{\mathop {\leadsto }\limits ^{\ell }} f)}\).
Now, find \({\mathbf {x}}\in {\mathcal {X}}\) such that \(x^\uparrow _n=a\), \(x^\uparrow _m=c\), and \(x^\uparrow _\ell =e\), and such that \(b_{(n)}{\mathbf {x}}\), \(d_{(m)}{\mathbf {x}}\), and \(f_{(\ell )}{\mathbf {x}}\) are all well defined. Then combining (B1) and (B2) and the transitivity of the indifference relation \(\approx \), we get \( b_{(n)}{\mathbf {x}}\approx f_{(\ell )}{\mathbf {x}}\). Thus, \({(a{\mathop {\leadsto }\limits ^{n}} b)} \cong {(e{\mathop {\leadsto }\limits ^{\ell }} f)}\).
\(\diamond \) Claim 1
Let \({\mathbb {R}}^{N_{\uparrow \uparrow }}:=\{{\mathbf {x}}\in {\mathbb {R}}^N\); \(x_1<x_2<\cdots <x_N\}\); this is the topological interior of \({\mathbb {R}}^{N_\uparrow }\) as a subset of \({\mathbb {R}}^N\). Let \({\mathcal {W}}\subseteq {\mathbb {R}}^{N_{\uparrow \uparrow }}\). The order \(\succeq _N\) is coordinate-independent on \({\mathcal {W}}\) if the following is true: for any \({\mathbf {w}},{\mathbf {v}},{\mathbf {w}}',{\mathbf {v}}'\in {\mathbb {R}}^{N_\uparrow }\), and any \(n\in [1\ldots N]\) such that \(w_n=v_n\) and \(w'_n=v'_n\), while \({\mathbf {w}}_{-n}={\mathbf {w}}'_{-n}\) and \({\mathbf {v}}_{-n}={\mathbf {v}}'_{-n}\), we have \({\mathbf {w}}\succeq _N {\mathbf {v}}\) if and only if \({\mathbf {w}}'\succeq _N {\mathbf {v}}'\). Say that \(\succeq _N\) is locally coordinate-independent on \({\mathbb {R}}^{N_{\uparrow \uparrow }}\) if it is coordinate-independent in an open neighbourhood of every point in \({\mathbb {R}}^{N_{\uparrow \uparrow }}\).
Claim 2
For every \(N\in {\mathbb {N}}\), the order \(\succeq _N\) is locally coordinate-independent on \({\mathbb {R}}^{N_{\uparrow \uparrow }}\).
Proof
Let \({\mathbf {x}}\in {\mathbb {R}}^{N_{\uparrow \uparrow }}\). Since \({\mathbb {R}}^{N_{\uparrow \uparrow }}\) is an open subset of \({\mathbb {R}}^N\), it contains an open neighbourhood around \({\mathbf {x}}\)—in other words, \({\mathbf {y}}\in {\mathbb {R}}^{N_{\uparrow \uparrow }}\) for all points \({\mathbf {y}}\in {\mathbb {R}}^N\) that are “close enough” to \({\mathbf {x}}\). Throughout this proof, when I use the words close enough, I will mean them in this way: the construction I want to perform involves a small enough change in coordinate values that it does not change the strict ordering of the coordinates.
Now, fix \(n\in [1\ldots N]\). Let \({\mathbf {x}},{\mathbf {y}},{\mathbf {x}}',{\mathbf {y}}'\) all be close enough together, and suppose that \(x_n=y_n\) and \(x'_n=y'_n\), while \({\mathbf {x}}_{-n}={\mathbf {x}}'_{-n}\) and \({\mathbf {y}}_{-n}={\mathbf {y}}'_{-n}\). I will show that \({\mathbf {x}}\succeq _N {\mathbf {y}}\) if and only if \({\mathbf {x}}'\succeq _N {\mathbf {y}}'\).
For simplicity, suppose \(n=1\) (the same argument works in general). So \({\mathbf {x}}=(a,x_2,x_3,\ldots ,x_N)\) and \({\mathbf {y}}=(a,y_2,y_3,\ldots ,y_N)\), while \({\mathbf {x}}'=(b,x_2,x_3,\ldots ,x_N)\) and \({\mathbf {y}}'=(b,y_2,y_3,\ldots ,y_N)\), for some \(x_2<\cdots <x_N\) and \(y_2<\cdots <y_N\) and some \(a,b<\min \{x_2,y_2\}\).
Let \(a^1:=a\). If \(y_2\) is close enough to \(x_2\), then Continuity and Pareto yield some \(a^2\in {\mathbb {R}}\) such that \((a^2,x_2,x_3,x_4,\ldots ,x_N)\approx _N (a^1,y_2,x_3,x_4,\ldots ,x_N)\).Footnote 30 In other words, \({(a^1{\mathop {\leadsto }\limits ^{1}} a^2)} \cong {(x_2{\mathop {\leadsto }\limits ^{2}} y_2)}\).
Next, if \(y_3\) is close enough to \(x_3\), then Continuity and Pareto yield some \(a^3\in {\mathbb {R}}\) such that \((a^3,x_2,x_3,x_4,\ldots ,x_N)\approx _N (a^2,x_2,y_3,x_4,\ldots ,x_N)\). In other words, \({(a^2{\mathop {\leadsto }\limits ^{1}} a^3)} \cong {(x_3{\mathop {\leadsto }\limits ^{3}} y_3)}\).
Now let \(n\in [4\ldots N]\), and suppose we have constructed \(a^{n-1}\). If \(y_{n}\) is close enough to \(x_{n}\), then Continuity and Pareto yield some \(a^{n}\in {\mathbb {R}}\) such that
In other words,
Now, by repeatedly applying Trade-off Consistency to the relations (B3), we obtain:
(If \({\mathbf {x}}\) and \({\mathbf {y}}\) are close enough, then all of these intermediate vectors are in \({\mathbb {R}}^{N_{\uparrow \uparrow }}\).) Thus,

Here \((*)\) is because \({\mathbf {x}}=(a^1,x_2,x_3,\ldots ,x_N)\) (because \(a^1=a=x_1\)) and \({\mathbf {y}}\approx _N (a^N,x_2,x_3,\ldots ,x_N)\) by formula (B4). Meanwhile \((\dagger )\) is by Pareto.
Now let \(b^1:=b\). If \({\mathbf {x}}\) and \({\mathbf {y}}\) are close enough, then by repeating the preceding argument, we can construct a sequence \(b^2, b^3,\ldots ,b^N\in {\mathbb {R}}\) such that
By repeatedly applying Trade-off Consistency to (B6), we obtain:
where, if \({\mathbf {x}}'\) and \({\mathbf {y}}'\) are close enough, then all of these vectors are in \({\mathbb {R}}^{N_{\uparrow \uparrow }}\). Thus,

Now I will show that \(a^1\geqslant a^N\) if and only if \(b^1\geqslant b^N\). Let \({\mathbf {z}}=(z_1,z_2,\ldots ,z_{N+1})\) be some element of \({\mathbb {R}}^{N+1_{\uparrow \uparrow }}\) such that \(z_1=a^1\) and \(z_2>\max \{a_2,a_3,\ldots ,a_N,b_2,b_3,\ldots ,b_N\}\). Let \(c^1:=z_{N+1}\). Using Pareto and Continuity, we can construct \(c^2,c^3,\ldots ,c^N\) such that
and all these vectors are in \({\mathbb {R}}^{N+1_\uparrow }\). (This is possible if \(z_{N+1}\) is large enough, and \(|a_n-a_{n-1}|\) is small enough for all \(n\in [2\ldots N]\), which in turn is the case as long as \({\mathbf {y}}\) is close enough to \({\mathbf {x}}\).) In other words,
Since \(1\ne n\ne N+1\), we can combine equations (B3) and (B9) via Claim 1, to get
Then, combining equations (B6) and (B10) via Claim 1, we get
Thus, Trade-off Consistency yields
Thus,

where \((*)\) is by (B8), \((\dagger )\) is by (B12), and both use Pareto. Putting it all together, we obtain

as desired. Here, \((*)\) is by statement (B5), \((\dagger )\) is by statement (B13), and \((\ddagger )\) is by statement (B7).
For any \({\mathbf {x}}\in {\mathbb {R}}^{N_{\uparrow \uparrow }}\), we can obtain the equivalence (B14) for all \({\mathbf {y}},{\mathbf {x}}',{\mathbf {y}}'\in {\mathbb {R}}^{N_{\uparrow \uparrow }}\) that are close enough to \({\mathbf {x}}\). A similar argument works for all \(n\in [1\ldots N]\). Thus, \(\succeq _N\) is locally coordinate-independent on \({\mathbb {R}}^{N_{\uparrow \uparrow }}\). \(\diamond \) Claim 2
Using Claim 2 and a result of Wakker (1988), I will soon show that \(\succeq _N\) admits a “local” additive representation in a neighbourhood of each point in \({\mathbb {R}}^{N_{\uparrow \uparrow }}\). I will then combine all these local additive representations using a theorem of Chateauneuf and Wakker (1993). Just as in the proof of Theorem 1, I must first check that all the technical conditions of the Chateauneuf–Wakker theorem are satisfied; this is the purpose of Claims 3 to 5.
Claim 3
Let \(N\in {\mathbb {N}}\). Every indifference set of \(\succeq _N\) in \({\mathbb {R}}^{N_{\uparrow \uparrow }}\) is path-connected.
The proof of Claim 3 is similar to the proof of Claim 1.1, but somewhat simpler. First we need a preliminary result. Let \({\mathcal {Y}}^N:=\{{\mathbf {x}}\in {\mathbb {R}}^{N_{\uparrow \uparrow }}\); \(x_1=0\}\). For any \({\mathbf {y}}=(y_1,\ldots ,y_N)\in {\mathbb {R}}^{N_{\uparrow \uparrow }}\) and \(r\in {\mathbb {R}}\), define \(\tau ^r({\mathbf {y}}):= (y_1+r,y_2+r,\ldots ,y_N+r)\). The next claim is analogous to Claim 1.2.
Claim 4
Let \(N\in {\mathbb {N}}\), and let \({\mathbf {x}}\in {\mathbb {R}}^{N_{\uparrow \uparrow }}\). Let \({\mathcal {Z}}:=\{{\mathbf {z}}\in {\mathbb {R}}^{N_{\uparrow \uparrow }}\); \({\mathbf {z}}\approx _N {\mathbf {x}}\}\) be the indifference set of \({\mathbf {x}}\). For any \({\mathbf {y}}\in {\mathcal {Y}}^N\), there is a unique \(r\in {\mathbb {R}}\) with \(\tau ^r({\mathbf {y}}) \in {\mathcal {Z}}\). Let \(\phi ({\mathbf {y}}):=\tau ^r({\mathbf {y}})\); this defines a continuous surjection \(\phi :{\mathcal {Y}}^N{{\longrightarrow }}{\mathcal {Z}}\).
Proof
Existence and uniqueness Since \({\mathbb {R}}^{N_{\uparrow \uparrow }}\) is a connected, separable topological space, and \(\succeq _N\) satisfies Continuity, the theorem of Debreu (1954) yields a continuous function \(w:{\mathbb {R}}^{N_{\uparrow \uparrow }}{{\longrightarrow }}{\mathbb {R}}\) that represents \(\succeq _N\). If r is large enough, then every coordinate of \(\tau ^r({\mathbf {y}})\) is bigger than every coordinate of \({\mathbf {x}}\), so Pareto says that \(\tau ^r({\mathbf {y}})\succeq _N{\mathbf {x}}\), and hence, \(w[\tau ^r({\mathbf {y}})]\geqslant w({\mathbf {x}})\). If r is small enough, then every coordinate of \(\tau ^r({\mathbf {y}})\) is smaller than every coordinate of \({\mathbf {x}}\), so Pareto says that \(\tau ^r({\mathbf {y}})\preceq _N{\mathbf {x}}\), and hence \(w[\tau ^r({\mathbf {y}})]\leqslant w({\mathbf {x}})\). The function \(w\mapsto w[\tau ^r({\mathbf {y}})]\) is continuous, so the intermediate value theorem yields some \(r\in {\mathbb {R}}\) such that \(w[\tau ^r({\mathbf {y}})]= w({\mathbf {x}})\), and hence, \(\tau ^r({\mathbf {y}})\approx _N{\mathbf {x}}\). Thus, \(\tau ^r({\mathbf {y}}) \in {\mathcal {Z}}\). This value of r is unique by Pareto.
Surjective Let \({\mathbf {z}}\in {\mathcal {Z}}\). Let \({\mathbf {y}}:=\tau ^{-z_1}({\mathbf {z}})\). Then \(y_1=0\) by construction, so \({\mathbf {y}}\in {\mathcal {Y}}^N\). Clearly, \(\tau ^{z_1}({\mathbf {y}})={\mathbf {z}}\). Thus, \(\phi ({\mathbf {y}})={\mathbf {z}}\).
Continuous In fact, \(\phi \) is Lipschitz continuous. To see this, let \({\mathbf {u}},{\mathbf {v}}\in {\mathcal {Y}}^N\) and let \(\epsilon :=\Vert {\mathbf {u}}-{\mathbf {v}}\Vert \). Then \(|u_n-v_n|\leqslant \epsilon \) for all \(n\in [1\ldots N]\). Let \({\mathbf {u}}':=\phi ({\mathbf {u}})\) and \({\mathbf {v}}':=\phi ({\mathbf {v}})\); then, there exist \(r,s\in {\mathbb {R}}\) such that \(u'_n=u_n+r\) and \(v'_n=v_n+s\) for all \(n\in [1\ldots N]\).
Suppose \(r>s+\epsilon \). Then for all \(n\in [1\ldots N]\), we have \(u'_n = u_n+r > u_n+s+\epsilon \geqslant v_n+s = v'_n\). So \({\mathbf {u}}'\succ _N {\mathbf {v}}\) by Pareto. This contradicts the fact that both \({\mathbf {u}}'\) and \({\mathbf {v}}'\) are in the same indifference set \({\mathcal {Z}}\).
Likewise, if \(r<s-\epsilon \), then \(u'_n<v'_n\) for all \(n\in [1\ldots N]\), so \({\mathbf {u}}'\prec _N {\mathbf {v}}\) by Pareto, again contradicting the fact that they are in the same indifference set. To avoid these contradictions, we must have \(|r-s|\leqslant \epsilon \). But \(\Vert {\mathbf {u}}' - {\mathbf {v}}'\Vert \leqslant \Vert {\mathbf {u}}-{\mathbf {v}}\Vert + N|r-s|\), and \(\epsilon =\Vert {\mathbf {u}}-{\mathbf {v}}\Vert \). Thus, \(\Vert {\mathbf {u}}' - {\mathbf {v}}'\Vert \leqslant (N+1)\, \Vert {\mathbf {u}}- {\mathbf {v}}\Vert \).
For any \({\mathbf {u}},{\mathbf {v}}\in {\mathcal {Y}}^N\), this argument yields \(\Vert \phi ({\mathbf {u}})-\phi ({\mathbf {v}})\Vert \leqslant (N+1) \Vert {\mathbf {u}}-{\mathbf {v}}\Vert \).
\(\diamond \) Claim 4
Proof of Claim 3
\({\mathcal {Y}}^N\) is the intersection of the hyperplane \(\{{\mathbf {x}}\in {\mathbb {R}}^N\); \(x_1=0\}\) with the convex set \({\mathbb {R}}^{N_{\uparrow \uparrow }}\), so \({\mathcal {Y}}^N\) is convex, hence path-connected. If \({\mathcal {Z}}\) is any indifference set of \(\succeq _N\), then Claim 4 says that \({\mathcal {Z}}\) is the image of \({\mathcal {Y}}^N\) under a continuous surjection; hence, \({\mathcal {Z}}\) is also path-connected. \(\diamond \) Claim 3
Recall the matching terminology introduced by Chateauneuf and Wakker (1993) and reviewed in the proof of Theorem 1. The next result plays the role of Claim 1.5.
Claim 5
Every element of \({\mathbb {R}}^{N_\uparrow }\) is matched.
Proof
Let \({\mathbf {x}}\in {\mathbb {R}}^{N_\uparrow }\). It is easy to see that is some \({\mathbf {y}}\in {\mathbb {R}}^{N_{\uparrow \uparrow }}\) such that \({\mathbf {x}}\approx _N {\mathbf {y}}\). (This can be proved by a perturbation argument using Pareto and Continuity. It is similar to the proof of Claim 1.4, so the details are left to the reader.) Second, for every \(n\in [1\ldots N]\), we can find some \({\mathbf {y}}\in {\mathbb {R}}^{N_{\uparrow \uparrow }}\) such that \(y_n=x_n\). Thus, \({\mathbf {x}}\) is interior-matched, and hence, matched. \(\diamond \) Claim 5
The next result is analogous to Claim 1.6.
Claim 6
For any \(N\in {\mathbb {N}}\) with \(N\geqslant 3\), there exists a unique collection of functions \(\psi ^N_{1},\ldots ,\psi ^N_{N}:{\mathbb {R}}{{\longrightarrow }}{\mathbb {R}}\) with \(\psi ^N_{1}(1)=1\) and with \(\psi ^N_{n}(0)=0\) for all \(n\in [1\ldots N]\), such that for any \({\mathbf {x}},{\mathbf {y}}\in {\mathbb {R}}^{N_\uparrow }\), we have

Proof
The proof strategy is similar to the proof of Claim 1.6: first, I construct a “local” additive representation in a neighbourhood of each point, and then, I stitch these local representations together using a result of Chateauneuf and Wakker (1993).
For any \({\mathbf {x}}\in {\mathbb {R}}^{N_{\uparrow \uparrow }}\), Claim 2 yields an open neighbourhood \({\mathcal {O}}\subset {\mathbb {R}}^{N_{\uparrow \uparrow }}\) with \({\mathbf {x}}\in {\mathcal {O}}\), such that \(\succeq _N\) is coordinate-independent when restricted to \({\mathcal {O}}\). Let \({\mathcal {B}}\subset {\mathcal {O}}\) be an open box containing \({\mathbf {x}}\)—say, \({\mathcal {B}}=(a_1,z_1)\times \cdots \times (a_{N},z_{N})\) for some \(a_1<z_1\), \(\ldots \), \(a_{N}<z_{N}\). Let \(\succeq _{\mathcal {B}}\) be the restriction of \(\succeq _N\) to \({\mathcal {B}}\). Then \(\succeq _{\mathcal {B}}\) is coordinate-independent (by Claim 2) and continuous (by Continuity). Thus, Theorem 4.1 of Wakker (1988) says that there are continuous, increasing functions \(\psi ^{\mathcal {B}}_n:(a_n,z_n){{\longrightarrow }}{\mathbb {R}}\) for all \(n\in [1\ldots N]\) such that, for any \({\mathbf {b}},{\mathbf {c}}\in {\mathcal {B}}\), we have

\({\mathbb {R}}^{N_{\uparrow \uparrow }}\) is open, so it can be covered by such open boxes. Thus, \(\succeq _N\) admits “local” additive representations (B16) everywhere on \({\mathbb {R}}^{N_{\uparrow \uparrow }}\). Since \({\mathbb {R}}^{N_{\uparrow \uparrow }}\) is convex, it clearly satisfies conditions (1) and (2) in Structural Assumption 2.1 of Chateauneuf and Wakker (1993). Meanwhile, condition (3) of Chateauneuf and Wakker (1993) is true by Claim 3. Finally, \({\mathbb {R}}^{N_{\uparrow \uparrow }}\) is the interior of \({\mathbb {R}}^{N_\uparrow }\), and every coordinate of any element on the boundary of \({\mathbb {R}}^{N_\uparrow }\) is matched, by Claim 5. Thus, by Theorem 3.3 of Chateauneuf and Wakker (1993), the local additive representations (B16) can be combined together to yield a single global additive representation (B15) on all of \({\mathbb {R}}^{N_\uparrow }\) . Furthermore, the functions \(\psi _1,\ldots ,\psi _N\) are unique up to increasing affine transformation with a common scalar multiplication.
For all \(n\in [1\ldots N]\), let \(k_n:=\psi _n(0)\). By replacing \(\psi _n\) with the function \(\psi _n-k_n\) if necessary, we can assume without loss of generality that \(\psi _n(0)=0\) for all \(n\in [1\ldots N]\). Now let \(s:=\psi _1(1)\). By replacing \(\psi _n\) with the function \(\psi _n/s\) for all \(n\in [1\ldots N]\) if necessary, we can assume without loss of generality that \(\psi _1(1)=1\).
For every \(N\in {\mathbb {N}}\), we can repeat the above construction. That is, for all \(N\in {\mathbb {N}}\), we obtain a collection of functions \(\psi ^N_{1},\ldots ,\psi ^N_{N}:{\mathbb {R}}{{\longrightarrow }}{\mathbb {R}}\) yielding an additive representation (B15) for \(\succeq _N\), and furthermore such that \(\psi ^N_{1}(1)=1\) and \(\psi ^N_{n}(0)=0\) for all \(n\in [1\ldots N]\). \(\diamond \) Claim 6
Now I will show that these additive representations agree for different values of N.
Claim 7
There is single infinite sequence of functions \((\phi _n)_{n=1}^{\infty }\) such that
Proof
Let \(N,M\in {\mathbb {N}}\), and let \(n\in [1\ldots N]\). I will show that \(\psi ^N_{n}=\psi ^M_{n}\). Let \(a,b\in {\mathbb {R}}\), let \(m\in [1\ldots N]\) with \(m\ne n\), and suppose there exist some \(c,d\in {\mathbb {R}}\) such that \(\psi ^N_n(b)-\psi ^N_n(a) = \psi ^N_m(d)-\psi ^N_m(c)\). (Such a c and d always exist if a and b are close enough together.) Thus, if \({\mathbf {x}}\in {\mathcal {X}}_N\) is any social outcome such that \(x^\uparrow _n=a\) and \(x^\uparrow _m=c\), and \(b_{(n)}{\mathbf {x}}\) and \(d_{(m)}{\mathbf {x}}\) are well defined, then the additive representation (B15) yields \(b_{(n)}{\mathbf {x}}\approx d_{(m)}{\mathbf {x}}\). Thus, \({(a{\mathop {\leadsto }\limits ^{n}} b)} \cong {(c{\mathop {\leadsto }\limits ^{m}} d)}\).
Now, for any \(M,L\in {\mathbb {N}}\), find \({\mathbf {y}}\in {\mathcal {X}}_M\) and \({\mathbf {z}}\in {\mathcal {X}}_L\) such that \(y^\uparrow _n=a\) and \(z^\uparrow _m=c\), \(b_{(n)}{\mathbf {y}}\) and \(d_{(m)}{\mathbf {z}}\) are well defined, and \({\mathbf {y}}\approx {\mathbf {z}}\). Then Trade-off Consistency says that \(b_{(n)}{\mathbf {y}}\approx d_{(m)}{\mathbf {z}}\). Thus, \(\psi ^M_n(b)-\psi ^M_n(a) = \psi ^L_m(d)-\psi ^L_m(c)\). Note that this equation holds for any \(L\in {\mathbb {N}}\). In particular, it holds for \(L=N\); thus, \(\psi ^M_n(b)-\psi ^M_n(a) = \psi ^N_m(d)-\psi ^N_m(c)\). But \( \psi ^N_m(d)-\psi ^N_m(c) = \psi ^N_n(b)-\psi ^N_n(a)\) by construction of c and d. Thus, we conclude that \(\psi ^M_n(b)-\psi ^M_n(a) =\psi ^N_n(b)-\psi ^N_n(a)\).
This argument works for any sufficiently close \(a,b\in {\mathbb {R}}\). Thus, for any \(a\in {\mathbb {R}}\), there is some \(\epsilon >0\) such that \(\psi ^M_n(b)-\psi ^M_n(a) =\psi ^N_n(b)-\psi ^N_n(a)\) for all \(b\in (a-\epsilon ,a+\epsilon )\). Since \({\mathbb {R}}\) can be covered with overlapping intervals like this, we conclude that \(\psi ^M_n(b)-\psi ^M_n(a) =\psi ^N_n(b)-\psi ^N_n(a)\) for all \(a,b\in {\mathbb {R}}\). Thus, there is some constant \(k\in {\mathbb {R}}\) such that \(\psi ^M_n=\psi ^N_n + k\). But \(\psi ^M_n(0)=0=\psi ^N_n(0)\) by the construction in Claim 6. Thus, \(k=0\). Thus, \(\psi ^M_n=\psi ^N_n\).
This argument works for all \(N<M\in {\mathbb {N}}\) and all \(n\in [1\ldots N]\). \(\diamond \) Claim 7
For any \({\mathbf {x}}\in {\mathcal {X}}_\propto \), we define \(\varPhi ({\mathbf {x}}):=\sum _{n=1}^N \phi _n(x^\uparrow _n)\), where \(N:=|{\mathbf {x}}|\). For any \({\mathbf {x}},{\mathbf {y}}\in {\mathcal {X}}_\propto \) with \(|{\mathbf {x}}|=|{\mathbf {y}}|\), Claims 6 and 7 together imply that

It remains to show that statement (B18) also holds when \(|{\mathbf {x}}|\ne |{\mathbf {y}}|\). For any \(M,N\in {\mathbb {N}}\), let \({\mathcal {I}}_{M,N}:=\{r\in {\mathbb {R}}\); there exist \({\mathbf {x}}\in {\mathcal {X}}_N\) and \({\mathbf {y}}\in {\mathcal {X}}_M\) such that \({\mathbf {x}}\approx {\mathbf {y}}\) and \(\varPhi ({\mathbf {x}})=r\}\).
Claim 8
\({\mathcal {I}}_{M,N}\) is an nonempty interval. Thus, for any \(r\in {\mathbb {R}}\), if \(r\not \in {\mathcal {I}}_{M,N}\), then either \(r<s\) for all \(s\in {\mathcal {I}}_{M,N}\), or \(r>s\) for all \(s\in {\mathcal {I}}_{M,N}\). In particular, for any \({\mathbf {y}}\in {\mathcal {X}}_N\),
- (a):
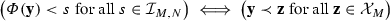 .
.- (b):
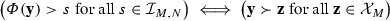 .
.
Proof
Nonempty For any \(N\in {\mathbb {N}}\), Neutral population growth yields some \({\mathbf {x}}_N\in {\mathcal {X}}_N\) such that \({\mathbf {x}}_N\approx \emptyset \). Let \(s:=\varPhi ({\mathbf {x}}_N)\). Then \(s\in {\mathcal {I}}_{M,N}\), because \({\mathbf {x}}_N\approx {\mathbf {x}}_M\), and \({\mathbf {x}}_M\in {\mathcal {X}}_M\).
Interval Let \(r,t\in {\mathcal {I}}_{M,N}\), with \(r<t\). We claim that \([r,t]\subseteq {\mathcal {I}}_{M,N}\). To see this, let \(s\in (r,t)\). There exists some \({\mathbf {x}},{\mathbf {z}}\in {\mathcal {X}}_N\) such that \(\varPhi ({\mathbf {x}})=r\) and \(\varPhi ({\mathbf {z}})=t\), and such that \({\mathbf {x}}\approx {\mathbf {x}}'\) and \({\mathbf {z}}\approx {\mathbf {z}}'\) for some \({\mathbf {x}}',{\mathbf {z}}'\in {\mathcal {X}}_M\). Define \(\varPhi _N:{\mathbb {R}}^{N_\uparrow }{{\longrightarrow }}{\mathbb {R}}\) by setting \(\varPhi _N({\mathbf {y}}):=\sum _{n=1}^N \phi _n(y_n)\) for all \({\mathbf {y}}=(y_1,\ldots ,y_N)\in {\mathbb {R}}^{N_\uparrow }\); then, \(\varPhi _N\) is continuous (because each of \(\phi _1,\ldots ,\phi _N\) is continuous). Since \(\varPhi _N({\mathbf {x}}^\uparrow )=r\) and \(\varPhi _N({\mathbf {z}}^\uparrow )=t\), and \({\mathbb {R}}^{N_\uparrow }\) is connected, the intermediate value theorem yields some \({\mathbf {v}}\in {\mathbb {R}}^{N_\uparrow }\) such that \(\varPhi _N({\mathbf {v}})=s\). Let \({\mathbf {y}}\in {\mathcal {X}}_N\) such that \({\mathbf {y}}^\uparrow ={\mathbf {v}}\); then, \(\varPhi ({\mathbf {y}})=s\). By statement (B18), we have \({\mathbf {x}}\prec {\mathbf {y}}\prec {\mathbf {z}}\), because \(r<s<t\).
Let \({\mathcal {A}}:=\{{\mathbf {a}}^\uparrow \); \({\mathbf {a}}\in {\mathcal {X}}_M\) and \({\mathbf {a}}\succ {\mathbf {y}}\}\) and \({\mathcal {B}}:=\{{\mathbf {b}}^\uparrow \); \({\mathbf {b}}\in {\mathcal {X}}_M\) and \({\mathbf {b}}\prec {\mathbf {y}}\}\). By the axiom Continuity, these are both open subsets of \({\mathbb {R}}^{M_\uparrow }\). Clearly, they are disjoint. Furthermore, both are nonempty, because \(({\mathbf {x}}')^\uparrow \in {\mathcal {B}}\) and \(({\mathbf {z}}')^\uparrow \in {\mathcal {A}}\) (because \({\mathbf {x}}'\approx {\mathbf {x}}\prec {\mathbf {y}}\) and \({\mathbf {z}}'\approx {\mathbf {z}}\succ {\mathbf {y}}\)). Thus, there must be some \(({\mathbf {y}}')^\uparrow \in {\mathbb {R}}^{M_\uparrow }\) such that \({\mathbf {y}}'\approx {\mathbf {y}}\)—otherwise, \({\mathbb {R}}^{M_\uparrow }={\mathcal {A}}\sqcup {\mathcal {B}}\), which contradicts the fact that \({\mathbb {R}}^{M_\uparrow }\) is connected. Since \(s=\varPhi ({\mathbf {y}})\) and \({\mathbf {y}}\approx {\mathbf {y}}'\), it follows that \(s\in {\mathcal {I}}_{M,N}\), as desired. This argument works for any \(r,t\in {\mathcal {I}}_{M,N}\) and \(s\in [r,t]\); it follows that \({\mathcal {I}}_{M,N}\) is an interval.
(a) “\(\Longrightarrow \)” (by contradiction) Let \({\mathbf {y}}\in {\mathcal {X}}_N\), and suppose \(\varPhi ({\mathbf {y}})< s\) for all \(s\in {\mathcal {I}}_{M,N}\), but also suppose \({\mathbf {y}}\succeq {\mathbf {z}}'\) for some \({\mathbf {z}}'\in {\mathcal {X}}_M\). Now, \({\mathcal {I}}_{M,N}\) is nonempty, so let \(s\in {\mathcal {I}}_{M,N}\), and let \({\mathbf {x}}\in {\mathcal {X}}_N\) such that \(\varPhi ({\mathbf {x}})=s\). We have \(\varPhi ({\mathbf {y}})< s=\varPhi ({\mathbf {x}})\), and hence, \({\mathbf {y}}\prec {\mathbf {x}}\) by statement (B18). Meanwhile, there is some \({\mathbf {x}}'\in {\mathcal {X}}_M\) such that \({\mathbf {x}}\approx {\mathbf {x}}'\), by definition of \({\mathcal {I}}_{M,N}\). Thus, \({\mathbf {y}}\prec {\mathbf {x}}'\). Meanwhile, \({\mathbf {y}}\succeq {\mathbf {z}}'\). By repeating the argument in the previous paragraph (using Continuity and the connectedness of \({\mathbb {R}}^{M_\uparrow }\)), we can construct some \({\mathbf {y}}'\in {\mathcal {X}}_M\) such that \({\mathbf {y}}\approx {\mathbf {y}}'\). But then \(\varPhi ({\mathbf {y}})\in {\mathcal {I}}_{M,N}\), which is a contradiction. To avoid the contradiction, we must have \({\mathbf {y}}\prec {\mathbf {z}}'\).
“\({\Longleftarrow }\)” Suppose \({\mathbf {y}}\prec {\mathbf {z}}\) for all \({\mathbf {z}}\in {\mathcal {X}}_M\). Let \(s\in {\mathcal {I}}_{M,N}\). Then \(s=\varPhi ({\mathbf {x}})\) for some \({\mathbf {x}}\in {\mathcal {X}}_N\), with some \({\mathbf {x}}'\in {\mathcal {X}}_M\) such that \({\mathbf {x}}\approx {\mathbf {x}}'\). But then \({\mathbf {y}}\prec {\mathbf {x}}'\); hence, \({\mathbf {y}}\prec {\mathbf {x}}\); hence, \(\varPhi ({\mathbf {y}})<\varPhi ({\mathbf {x}})=s\), by statement (B18), as desired.
The proof of (b) is very similar to the proof of (a). \(\diamond \) Claim 8
For any \(r\in {\mathcal {I}}_{M,N}\), find \({\mathbf {x}}\in {\mathcal {X}}_N\) such that \(\varPhi ({\mathbf {x}})=r\). Then find \({\mathbf {y}}\in {\mathcal {X}}_M\) with \({\mathbf {x}}\approx {\mathbf {y}}\), and define \(V_{N,M}(r):=\varPhi ({\mathbf {y}})\). Then \(V_{N,M}(r)\in {\mathcal {I}}_{N,M}\).
Claim 9
\(V_{N,M}(r)\) is well defined independent of the particular choice of \({\mathbf {x}}\) and \({\mathbf {y}}\).
Proof
Let \({\mathbf {x}}'\in {\mathcal {X}}_N\) and \({\mathbf {y}}'\in {\mathcal {X}}_M\), and suppose that \(\varPhi ({\mathbf {x}}')=r\) and \({\mathbf {x}}'\approx {\mathbf {y}}'\). Then \({\mathbf {y}}'\approx {\mathbf {x}}'\approx {\mathbf {x}}\approx {\mathbf {y}}\) (where the middle indifference is by (B18), because \(\varPhi ({\mathbf {x}}')= r=\varPhi ({\mathbf {x}})\)) hence \({\mathbf {y}}'\approx {\mathbf {y}}\) (by transitivity), and hence \(\varPhi ({\mathbf {y}}')=\varPhi ({\mathbf {y}})\) [by (B18)]. \(\diamond \) Claim 9
This yields a function \(V_{M,N}:{\mathcal {I}}_{M,N}{{\longrightarrow }}{\mathcal {I}}_{N,M}\). It is easily verified that \(V_{M,N}\) is an increasing bijection from \({\mathcal {I}}_{M,N}\) to \({\mathcal {I}}_{N,M}\), and \(V_{M,N}^{-1}=V_{N,M}\), as a function from \({\mathcal {I}}_{N,M}\) back to \({\mathcal {I}}_{M,N}\).
Claim 10
For any \({\mathbf {x}}\in {\mathcal {X}}_N\) and \({\mathbf {y}}\in {\mathcal {X}}_M\), if \(\varPhi ({\mathbf {x}})\in {\mathcal {I}}_{M,N}\), then

Proof
Let \(r:=\varPhi ({\mathbf {x}})\), and let \(r':=V_{M,N}(r)\). Then there is some \({\mathbf {x}}'\in {\mathcal {X}}_M\) such that \({\mathbf {x}}\approx {\mathbf {x}}'\) and \(\varPhi ({\mathbf {x}}')=r'\). Let \(s:=\varPhi ({\mathbf {y}})\). If \(s\leqslant r'\), then representation (B18) yields \({\mathbf {y}}\preceq {\mathbf {x}}' \). Meanwhile, \({\mathbf {x}}'\approx {\mathbf {x}}\); thus, \({\mathbf {y}}\preceq {\mathbf {x}}\), by transitivity. If \(s\geqslant r'\), then representation (B18) yields \({\mathbf {y}}\succeq {\mathbf {x}}'\). Meanwhile, \({\mathbf {x}}'\approx {\mathbf {x}}\); thus, \({\mathbf {y}}\succeq {\mathbf {x}}\), by transitivity. \(\diamond \) Claim 10
Claim 11
For any \(n< m\in {\mathbb {N}}\) and \(a < c\in {\mathbb {R}}\), there exists \(\epsilon >0\) and a continuous, increasing function \(\psi :(a-\epsilon ,a+\epsilon ){{\longrightarrow }}{\mathbb {R}}\) with \(\psi (a)=c\), such that for all \(b\in (a-\epsilon ,a+\epsilon )\), if \(d:=\psi (b)\), then \({(a{\mathop {\leadsto }\limits ^{n}} b)} \cong {(c{\mathop {\leadsto }\limits ^{m}} d)}\).
Proof
Let \({\mathbf {x}}\in {\mathcal {X}}_\propto \) such that \(x^\uparrow _{n-1}<x^\uparrow _n=a<x^\uparrow _{n+1}\) and \(x^\uparrow _{m-1}<x^\uparrow _m=c<x^\uparrow _{m+1}\). Let \(N:=|{\mathbf {x}}|\). Since \(\phi _m\) is continuous and strictly increasing, its image \({\mathcal {R}}_m:=\phi _m({\mathbb {R}})\) is an open interval in \({\mathbb {R}}\), and \(\phi _m:{\mathbb {R}}{{\longrightarrow }}{\mathcal {R}}_m\) is a homeomorphism. Likewise, if \({\mathcal {R}}_n:=\phi _n({\mathbb {R}})\), then \({\mathcal {R}}_n\) is an open interval and \(\phi _n:{\mathbb {R}}{{\longrightarrow }}{\mathcal {R}}_n\) is a homeomorphism. Let \({\mathcal {R}}'_m:=\{r-\phi _m(c)+\phi _n(a)\); \(r\in {\mathcal {R}}_m\}\); then, \(\phi _n(a)\in {\mathcal {R}}'_m\) (because \(\phi _m(c)\in {\mathcal {R}}_m\)), and thus, \({\mathcal {R}}'_m\cap {\mathcal {R}}_n\) is itself a nonempty open interval containing \(\phi _n(a)\). Let \({\mathcal {Q}}_n:=\phi _n^{-1}({\mathcal {R}}'_m\cap {\mathcal {R}}_n)\); then, \({\mathcal {Q}}_n\) is an open interval containing a. Now define \(\psi :{\mathcal {Q}}_n{{\longrightarrow }}{\mathbb {R}}\) by setting
Then \(\psi (a)=c\). If \({\mathcal {Q}}_m:=\psi ({\mathcal {Q}}_n)\), then \({\mathcal {Q}}_m\) is an open interval containing c, and \(\psi \) is a continuous, increasing bijection from \({\mathcal {Q}}_n\) to \({\mathcal {Q}}_m\). Let \({\mathcal {Q}}'_n:={\mathcal {Q}}_n\cap (x^\uparrow _{n-1},x^\uparrow _{n+1}) \cap \psi ^{-1}(x^\uparrow _{m-1},x^\uparrow _{m+1})\), and let \({\mathcal {Q}}'_m:=\psi ({\mathcal {Q}}'_n)\), then \({\mathcal {Q}}'_n\) and \({\mathcal {Q}}'_m\) are open intervals around a and c, respectively, and \(\psi :{\mathcal {Q}}'_n{{\longrightarrow }}{\mathcal {Q}}'_m\) is a continuous, increasing function.
For any \(b\in {\mathcal {Q}}'_n\), the element \(b_{(n)}{\mathbf {x}}\) is well defined because \(x^\uparrow _{n-1}<b<x^\uparrow _{n+1}\). If \(d:=\psi (b)\), then \(d_{(m)}{\mathbf {x}}\) is well defined because \(x^\uparrow _{m-1}<d<x^\uparrow _{m+1}\) because \(d\in {\mathcal {Q}}'_m\). Finally, \(b_{(n)}{\mathbf {x}}\approx d_{(m)}{\mathbf {x}}\) by statement (B18), because \(\varPhi (b_{(n)}{\mathbf {x}})=\varPhi (d_{(m)}{\mathbf {x}})\), because \(\phi _m(d)-\phi _m(c) = \phi _n(b)-\phi _n(a)\) by the definition of \(\psi \). Since \(x^\uparrow _n=a\) and \(x^\uparrow _m=c\), we conclude that \({(a{\mathop {\leadsto }\limits ^{n}} b)} \cong {(c{\mathop {\leadsto }\limits ^{m}} d)}\).
Now find \(\epsilon >0\) small enough that \((a-\epsilon ,a+\epsilon )\subseteq {\mathcal {Q}}'_n\). Then for any \(b\in (a-\epsilon ,a+\epsilon )\), if \(d=\psi (b)\), then \({(a{\mathop {\leadsto }\limits ^{n}} b)} \cong {(c{\mathop {\leadsto }\limits ^{m}} d)}\), by the previous paragraph.
\(\diamond \) Claim 11
Claim 12
For any \(M,N\in {\mathbb {N}}\), there exists a constant \(Q_{M,N}\in {\mathbb {R}}\) such that \(V_{M,N}(r)=r+Q_{M,N}\) for all \(r\in {\mathcal {I}}_{M,N}\).
Proof
Let \(r\in {\mathcal {I}}_{M,N}\). Find \({\mathbf {x}}\in {\mathcal {X}}_N\) with \(\varPhi ({\mathbf {x}})=r\), and find \({\mathbf {y}}\in {\mathcal {X}}_M\) such that \({\mathbf {x}}\approx {\mathbf {y}}\); then, \(V_{M,N}[\varPhi ({\mathbf {x}})]=\varPhi ({\mathbf {y}})\), by the definition of \(V_{M,N}\) and Claim 9. Find \(n,m\in [1\ldots N]\) such that \(x_{n-1}<x_n<x_{n+1}\) and \(y_{m-1}<y_m<y_{m+1}\). Let \(a:=x_n\) and \(c:=y_m\). Let \(\psi :(a-\epsilon ,a+\epsilon ){{\longrightarrow }}{\mathbb {R}}\) be as described in Claim 11; then, \(\psi (a)=c\). Define
Then \(\epsilon _0>0\). Let \(b\in (a-\epsilon _0,a+\epsilon _0)\), and let \(d:=\psi (b)\). If \(\delta :=\phi _n(b)-\phi _n(a)\), then also \(\phi _m(d)-\phi _m(c)=\delta \), because \({(a{\mathop {\leadsto }\limits ^{n}} b)} \cong {(c{\mathop {\leadsto }\limits ^{m}} d)}\) by the definition of \(\psi \) in Claim 11. If \({\mathbf {x}}':= b_{(n)}{\mathbf {x}}\) (which is well defined because \(b\in (x_{n-1},x_{n+1})\)), then \(\varPhi ({\mathbf {x}}')=\varPhi ({\mathbf {x}})+\delta \). Likewise, if \({\mathbf {y}}':=d_{(m)}{\mathbf {y}}\) [which is well defined because \(d=\psi (b)\) and \(b\in (\psi ^{-1}(y_{m-1}), \ \psi ^{-1}(y_{m+1}))\)], then \(\varPhi ({\mathbf {y}}')=\varPhi ({\mathbf {y}})+\delta \).
As \({\mathbf {x}}\approx {\mathbf {y}}\), \({\mathbf {x}}'\approx {\mathbf {y}}'\), by Trade-off Consistency. Thus, \(V_{M,N}[\varPhi ({\mathbf {x}}')]=\varPhi ({\mathbf {y}}')\), by Claim 10. In other words, \(V_{M,N}[\varPhi ({\mathbf {x}})+\delta ]=\varPhi ({\mathbf {y}})+\delta =V_{M,N}[\varPhi ({\mathbf {x}})]+\delta \).
This equality holds for any sufficiently small \(\delta \)—in particular, it holds for all \(\delta \) in the set \(\{\phi _n(b)-\phi _n(a)\); \(b\in (a-\epsilon _0,a+\epsilon _0)\}\), which is an open interval around zero. Thus, if \(r\in {\mathcal {I}}_{M,N}\) and \(s\in {\mathcal {I}}_{N,M}\) are any values such that \(V_{M,N}(r)=s\), then we also have \(V_{M,N}(r+\delta )=s+\delta \) for all sufficiently small \(\delta \). This shows that \(V_{M,N}\) is an affine function with slope 1 in a neighbourhood of each point in \({\mathcal {I}}_{M,N}\). But \({\mathcal {I}}_{M,N}\) is an interval by Claim 8; it follows that \(V_{M,N}\) is an affine function with slope 1 everywhere on \({\mathcal {I}}_{M,N}\). \(\diamond \) Claim 12
Based on Claim 12, we can extend \(V_{M,N}\) to an affine function \(V_{M,N}:{\mathbb {R}}{{\longrightarrow }}{\mathbb {R}}\), by defining \(V_{M,N}(r)=r+Q_{M,N}\) for all \(r\in {\mathbb {R}}\).
Claim 13
For any \({\mathbf {x}}\in {\mathcal {X}}_N\) and \({\mathbf {z}}\in {\mathcal {X}}_M\), 
Proof
Let \(r:=\varPhi ({\mathbf {x}})\) and let \(t:=\varPhi ({\mathbf {z}})\). If \(r\in {\mathcal {I}}_{M,N}\), then the stated equivalence follows from Claim 10. Likewise, if \(t\in {\mathcal {I}}_{N,M}\), then it follows from Claim 10 and the observation that \(V_{N,M}^{-1}=V_{M,N}\) and both are increasing, so that \(V_{M,N}[\varPhi ({\mathbf {x}})]\leqslant \varPhi ({\mathbf {z}})\) if and only if \(\varPhi ({\mathbf {x}})\leqslant V_{N,M}[\varPhi ({\mathbf {z}})]\).
So, suppose that \(r\not \in {\mathcal {I}}_{M,N}\) and \(t\not \in {\mathcal {I}}_{N,M}\). It follows that \({\mathbf {x}}\not \approx {\mathbf {z}}\) (because otherwise we would have both \(r\in {\mathcal {I}}_{M,N}\) and \(t\in {\mathcal {I}}_{N,M}\)). Thus, either \({\mathbf {x}}\prec {\mathbf {z}}\) or \({\mathbf {x}}\succ {\mathbf {z}}\).
Claim 13A
-
(a)
If\({\mathbf {x}}\prec {\mathbf {z}}\), then\(V_{M,N}[\varPhi ({\mathbf {x}})]< \varPhi ({\mathbf {z}})\).
-
(b)
If\({\mathbf {x}}\succ {\mathbf {z}}\), then\(V_{M,N}[\varPhi ({\mathbf {x}})]>\varPhi ({\mathbf {z}})\).
Proof
(a) Suppose \({\mathbf {x}}\prec {\mathbf {z}}\). Claim 8 says \({\mathcal {I}}_{M,N}\) is an interval. So, since \(r\not \in {\mathcal {I}}_{M,N}\), we must have either \(r<s\) for all \(s\in {\mathcal {I}}_{M,N}\), or \(r>s\) for all \(s\in {\mathcal {I}}_{M,N}\). If \(r>s\) for all \(s\in {\mathcal {I}}_{M,N}\), then Claim 8(b) says that \({\mathbf {x}}\succ {\mathbf {y}}\) for all \({\mathbf {y}}\in {\mathcal {X}}_M\), which contradicts the hypothesis that \({\mathbf {x}}\prec {\mathbf {z}}\). So, we must have \(r<s\) for all \(s\in {\mathcal {I}}_{M,N}\). By a similar logic [using Claim 8(a)], we must have \(t>s'\) for all \(s'\in {\mathcal {I}}_{N,M}\).
Now, let \(s\in {\mathcal {I}}_{M,N}\) and find some \({\mathbf {y}}\in {\mathcal {X}}_N\) such that \(\varPhi ({\mathbf {y}})=s\), and some \({\mathbf {y}}'\in {\mathcal {X}}_M\) such that \({\mathbf {y}}\approx {\mathbf {y}}'\). Thus, if \(s':=\varPhi ({\mathbf {y}}')\), then \(s'=V_{M,N}(s)\). Furthermore, \(s'\in {\mathcal {I}}_{N,M}\). By the previous paragraph, we have \(r<s\) and \(s'<t\). Thus, \(V_{N,M}(r)<V_{N,M}(s)=s'<t\). In other words, \(V_{M,N}[\varPhi ({\mathbf {x}})]< \varPhi ({\mathbf {z}})\).
The proof of (b) is similar. \(\triangledown \) Claim 13A
Claim 13B
\(V_{M,N}[\varPhi ({\mathbf {x}})]\ne \varPhi ({\mathbf {z}})\).
Proof
(by contradiction) Suppose \(V_{M,N}[\varPhi ({\mathbf {x}})]=\varPhi ({\mathbf {z}})\). By taking the contrapositive parts (a) and (b) of Claim 13A, we cannot have either \({\mathbf {x}}\prec {\mathbf {z}}\) or \({\mathbf {x}}\succ {\mathbf {z}}\). So we must have \({\mathbf {x}}\approx {\mathbf {z}}\), because \(\succeq \) is a complete relation. But we have already deduced that \({\mathbf {x}}\not \approx {\mathbf {z}}\), so this is a contradiction. \(\triangledown \) Claim 13B
It follows from Claim 13B that either \(V_{M,N}[\varPhi ({\mathbf {x}})]< \varPhi ({\mathbf {z}})\) or \(V_{M,N}[\varPhi ({\mathbf {x}})]>\varPhi ({\mathbf {z}})\). If \(V_{M,N}[\varPhi ({\mathbf {x}})]< \varPhi ({\mathbf {z}})\), then the contrapositive of Claim 13A(b) says that \({\mathbf {x}}\preceq {\mathbf {z}}\), and hence, \({\mathbf {x}}\prec {\mathbf {z}}\) (because \({\mathbf {x}}\not \approx {\mathbf {z}}\)). If \(V_{M,N}[\varPhi ({\mathbf {x}})]> \varPhi ({\mathbf {z}})\), then the contrapositive of Claim 13A(a) says that \({\mathbf {x}}\succeq {\mathbf {z}}\), and hence, \({\mathbf {x}}\succ {\mathbf {z}}\) (because \({\mathbf {x}}\not \approx {\mathbf {z}}\)). At this point, we have shown that \({\mathbf {x}}\prec {\mathbf {z}}\) if and only if \(V_{M,N}[\varPhi ({\mathbf {x}})]< \varPhi ({\mathbf {z}})\). Likewise, \({\mathbf {x}}\succ {\mathbf {z}}\), if and only if \(V_{M,N}[\varPhi ({\mathbf {x}})]>\varPhi ({\mathbf {z}})\). Since we also know that \({\mathbf {x}}\not \approx {\mathbf {z}}\) and \(V_{M,N}[\varPhi ({\mathbf {x}})]\ne \varPhi ({\mathbf {z}})\) (by Claim 13B), this suffices to prove the claimed equivalence. \(\diamond \) Claim 13
For all \(N,M\in {\mathbb {N}}\), let \(Q_{N,M}\) be as in Claim 12.
Claim 14
For all \(M,N\in {\mathbb {N}}\), we have \(Q_{M,N}=-Q_{N,M}\), and for all \(L\in {\mathbb {N}}\), we have \(Q_{L,M}+Q_{M,N}=Q_{L,N}\).
Proof
As already noted, \(V_{M,N}^{-1}=V_{N,M}\), as a function from \({\mathcal {I}}_{N,M}\) back to \({\mathcal {I}}_{M,N}\); thus, Claim 12 yields \(Q_{M,N}=-Q_{N,M}\).
Now consider the set \({\mathcal {I}}_{M,N}\cap V_{N,M}({\mathcal {I}}_{L,M})\). I claim this intersection is nonempty. To see this, for all \(\ell \in \{L,M,N\}\), let \({\mathbf {x}}_\ell \in {\mathcal {X}}_\ell \) be such that \({\mathbf {x}}_\ell \approx \emptyset \); such elements exist by Neutral population growth. If \(r:=\varPhi ({\mathbf {x}}_N)\), then \(r\in {\mathcal {I}}_{M,N}\) (because \({\mathbf {x}}_N\approx {\mathbf {x}}_M\)). Likewise, if \(s:=\varPhi ({\mathbf {x}}_M)\), then \(s\in {\mathcal {I}}_{L,M}\) (because \({\mathbf {x}}_M\approx {\mathbf {x}}_L\)). Finally, \(V_{N,M}(s)=r\), because \({\mathbf {x}}_M\approx {\mathbf {x}}_N\). Thus, \(r\in {\mathcal {I}}_{M,N}\cap V_{N,M}({\mathcal {I}}_{L,M})\); thus, \({\mathcal {I}}_{M,N}\cap V_{N,M}({\mathcal {I}}_{L,M})\ne \{\}\).
It is easily verified that \({\mathcal {I}}_{M,N}\cap V_{N,M}({\mathcal {I}}_{L,M})\subseteq {\mathcal {I}}_{L,N}\), and \(V_{L,M}\circ V_{M,N}(r) = V_{L,N}(r)\), for all \(r\in {\mathcal {I}}_{M,N}\cap V_{N,M}({\mathcal {I}}_{L,M})\). Thus, Claim 12 yields \(Q_{L,M}+Q_{M,N}=Q_{L,N}\). \(\diamond \) Claim 14
For all \(N\in {\mathbb {N}}\), let \(q_N:=Q_{N,N-1}\). (In particular, \(q_1=Q_{1,0}=V_{1,0}(0)= V_{1,0}[\varPhi (\emptyset )]=\phi _1(x_1)\), where \(x_1\in {\mathbb {R}}\) is the unique value such that if \({\mathbf {x}}\in {\mathcal {X}}_1\) is the one-person outcome with lifetime utility \(x_1\), then \({\mathbf {x}}\approx \emptyset \); such an \(x_1\) exists by Neutral population growth, and it is unique by Pareto.) For any \(N<M\), Claim 14 implies that \(Q_{M,N}= q_{N+1}+\cdots +q_M\). For all \(n\in {\mathbb {N}}\), define \(\phi '_n:=\phi _n-q_n\). For any \({\mathbf {x}}\in {\mathcal {X}}_\propto \), if \(N:=|{\mathbf {x}}|\), then define
Thus, for all \(M\in {\mathbb {N}}\) and \({\mathbf {y}}\in {\mathcal {X}}_M\),

as desired. Here, (a) is by Eq. (B19). Next, (b) is because \(Q_{M,0}- Q_{N,0}=Q_{M,N}\) by Claim 14, so that \(\varPhi ({\mathbf {x}}) + Q_{M,0}- Q_{N,0}=\varPhi ({\mathbf {x}}) + Q_{M,N}=V_{M,N}[\varPhi ({\mathbf {x}})]\). Finally, (c) is by Claim 13. \(\square \)
Remarks
In the proof of Theorem 2, Neutral population growth is only needed in Claims 8 and 14, where it is used to show that certain sets are not empty.
If we had assumed that \(\succeq \) satisfied an axiom of Separability similar to the one used in Sect. 2.2, then Claims 1–5 would be unnecessary, and the proof of Claim 6 could be made much simpler: we could just invoke Corollary 3.6 of Wakker (1993) to immediately obtain an additive representation of \(\succeq _N\) on all of \({\mathbb {R}}^{N_\uparrow }\). (This argument was used in an earlier version of this paper.)
Proof of Proposition 3.1
“(a) \(\Longrightarrow \) (b)” (by contradiction) Let \(I:=\inf (\phi _1({\mathbb {R}}))\). If statement (b) is false, then either \(I > -S({\varvec{\phi }})\), or \(I=-S({\varvec{\phi }})\) and supremum in formula (3F) is obtained.
Case 1 Suppose \(I > -S({\varvec{\phi }})\). Then \(-I< S({\varvec{\phi }})\). Thus, there exist \(x_1\leqslant x_2\leqslant \cdots \leqslant x_N\in {\mathbb {R}}\) such that \(\sum _{n=1}^N \delta \phi _n(x_n)>-I\). Find \({\mathbf {x}}\in {\mathcal {X}}_\propto \) such that \({\mathbf {x}}^\uparrow =(x_1,\ldots ,x_N)\). Suppose \(r<x_1\), and let \({\mathbf {y}}:={\mathbf {x}}\uplus r\). Then \({\mathbf {y}}^\uparrow =(r,x_1,\ldots ,x_N)\). Thus,
where \((*)\) is by definition of I. Thus, \(W({\mathbf {y}})>W({\mathbf {x}})\), so \({\mathbf {x}}\uplus r \succ {\mathbf {x}}\). This holds for all \(r<x_1\).
On the other hand, if \(s\geqslant x_1\), then \(s>r\) for any \(r<x_1\), and thus \({\mathbf {x}}\uplus s\succ {\mathbf {x}}\uplus r\) by Pareto, while \({\mathbf {x}}\uplus r \succ {\mathbf {x}}\) by the previous paragraph. Thus, \({\mathbf {x}}\uplus s\succ {\mathbf {x}}\) by transitivity. It follows that \({\mathbf {x}}\uplus s\succ {\mathbf {x}}\) for all\(s\in {\mathbb {R}}\). This contradicts the axiom Critical levels.
Case 2 Suppose \(I=-S({\varvec{\phi }})\) and supremum in formula (3F) is obtained. Then \(-I= S({\varvec{\phi }})\), and there exists some \(x_1\leqslant x_2\leqslant \cdots \leqslant x_N\in {\mathbb {R}}\) such that \(\sum _{n=1}^N \delta \phi _n(x_n)=-I\). Again, let \({\mathbf {x}}\in {\mathcal {X}}_\propto \) be such that \({\mathbf {x}}^\uparrow =(x_1,\ldots ,x_N)\), let \(r<x_1\), and let \({\mathbf {y}}:={\mathbf {x}}\uplus r\). Then by a similar computation to Case 1, we get
(Here, the last step is because \(\phi _1(r) >I\) because the infimum I is never obtained, since \(\phi _1\) is strictly increasing.) Thus, once again, \(W({\mathbf {y}})>W({\mathbf {x}})\); hence, \({\mathbf {x}}\uplus r \succ {\mathbf {x}}\). This argument holds for all \(r<x_1\). The rest of the argument is identical to Case 1; again, we obtain a contradiction of Critical levels.
“(b) \({\Longleftarrow }\) (a)” Suppose \(\succeq \) has an ARA representation satisfying the condition the theorem. To show that \(\succeq \) satisfies Critical levels, let \({\mathbf {x}}\in {\mathcal {X}}_\propto \). For any \(r\in {\mathbb {R}}\), define \(\psi (r)=W({\mathbf {x}}\uplus r)\). It is easily verified that \(\psi :{\mathbb {R}}{{\longrightarrow }}{\mathbb {R}}\) is a continuous function. To verify Critical levels, we must find some \(c\in {\mathbb {R}}\) such that \(\psi (c)=W({\mathbf {x}})\).
Claim 1
There exists \(d\in {\mathbb {R}}\) such that \(\psi (d)>W({\mathbf {x}})\).
Proof
Let \(N:=|{\mathbf {x}}|\), and let \({\mathbf {x}}^\uparrow =(x^\uparrow _1,\ldots ,x^\uparrow _N)\). By hypothesis, we have \(\phi _{N+1}(c_{N+1})=0\). Thus, \(\phi _{N+1}(d)>0\) for any \(d>c_{N+1}\). Suppose \(d>\max \{x^\uparrow _N,c_{N+1}\}\), and let \({\mathbf {d}}:={\mathbf {x}}\uplus d\). Then \({\mathbf {d}}^\uparrow =(x^\uparrow _1,\ldots ,x^\uparrow _N,d)\). Thus, \(\psi (d)=W({\mathbf {d}})=W({\mathbf {x}})+\phi _{N+1}(d) > W({\mathbf {x}})\), because \(\phi _{N+1}(d)>0\). \(\diamond \) Claim 1
Claim 2
There exists \(b\in {\mathbb {R}}\) with \(\displaystyle \phi _1(b)<-\sum \nolimits _{n=1}^N \delta \phi _n(x^\uparrow _n)\).
Proof
Let \(A:=\sum _{n=1}^N \delta \phi _n(x^\uparrow _n)\). Then \(S({\varvec{\phi }})\geqslant A\), so \(-S({\varvec{\phi }})\leqslant -A\). By hypothesis, \(\inf (\phi _1({\mathbb {R}}))\leqslant -S({\varvec{\phi }})\), and if \(\inf (\phi _1({\mathbb {R}}))= -S({\varvec{\phi }})\), then the supremum (3F) is not obtained. If \(\inf (\phi _1({\mathbb {R}}))< -S({\varvec{\phi }})\), then there is some \(b\in {\mathbb {R}}\) such that \(\phi _1(b)<-S({\varvec{\phi }})\), and hence, \(\phi _1(b)<-A\) as desired. On the other hand, if \(\inf (\phi _1({\mathbb {R}}))= -S({\varvec{\phi }})\), then the supremum (3F) is not obtained, so \(S(\phi )>A\). Thus, \(-S(\phi )<-A\), and hence \(\inf (\phi _1({\mathbb {R}}))<-A\), so there is some \(b\in {\mathbb {R}}\) such that \(\phi _1(b)<-A\), as desired.
\(\diamond \) Claim 2
Claim 3
There exists \(b\in {\mathbb {R}}\) with \(\psi (b)< W({\mathbf {x}})\).
Proof
Let \(b_0\in {\mathbb {R}}\) be as in Claim 2. Note that any \(b<b_0\) also satisfies the inequality in Claim 2. By making b small enough, we can assume that \(b<x^\uparrow _1\). Thus, if \({\mathbf {b}}={\mathbf {x}}\uplus b\), then \({\mathbf {b}}^\uparrow =(b,x^\uparrow _1,\ldots ,x^\uparrow _N)\). Thus,
Thus, \(\psi (b)=W({\mathbf {b}})<W({\mathbf {x}})\). \(\diamond \) Claim 3
From Claims 1 and 3, we have \(b,d\in {\mathbb {R}}\) such that \(\psi (b)<W({\mathbf {x}})<\psi (d)\). By the intermediate value theorem, there exists some \(c\in (b,d)\) such that \(\psi (c)=W({\mathbf {x}})\). Thus, \(W({\mathbf {x}}\uplus c)=W({\mathbf {x}})\), which means \({\mathbf {x}}\uplus c \approx {\mathbf {x}}\), as desired. \(\square \)
Proof of Proposition 3.2
The proof of (a) is similar to the proof of Proposition 2.2(a). The proof of parts (b) and (c) is similar to the proof of Proposition 2.4. \(\square \)
Proof of Proposition 3.4
(a) Instead of Minimal Aggregation, we will actually show that any ARA SWO satisfies the following, slightly stronger axiom:
Minimal Aggregation\(^+\) For any \(N\in {\mathbb {N}}\), any \(\alpha >0\) and all \({\mathbf {x}}\in {\mathcal {X}}_N\), there exists some \(\beta >0\) such that, for all \({\mathbf {y}}\in {\mathcal {X}}_\propto \) with \({\mathcal {I}}({\mathbf {y}})={\mathcal {I}}({\mathbf {x}})\), if there is some \(i\in {\mathcal {I}}({\mathbf {x}})\) such that \(x_i\geqslant y_i\geqslant x_i-\beta \), while \(y_j\geqslant x_j+\alpha \) for all other \(j\in {\mathcal {I}}({\mathbf {x}})\), then \({\mathbf {y}}\succeq {\mathbf {x}}\).
If we represent \(\succeq \) with an ordering \(\succeq _*\) on \({\mathbb {R}}^{\propto _\uparrow }\), as in formula (3A), then this axiom is equivalent to:
Minimal Aggregation* For any \(N\in {\mathbb {N}}\), any \(\alpha >0\) and all \({\mathbf {x}}\in {\mathbb {R}}^{N_\uparrow }\), there exists some \(\beta >0\) such that, for all \({\mathbf {y}}\in {\mathbb {R}}^N\), if there is some \(n\in [1\ldots N]\) such that \(x_n\geqslant y_n\geqslant x_n-\beta \), while \(y_n\geqslant x_n+\alpha \) for all other \(n\in [1\ldots N]\), then \({\mathbf {y}}^\uparrow \succeq _* {\mathbf {x}}\).
(Here, \({\mathbf {y}}^\uparrow \) is the vector obtained by reordering the components of \({\mathbf {y}}\) in increasing order.)
To prove this, let \(N\in {\mathbb {N}}\), and \({\mathbf {x}}\in {\mathbb {R}}^{N_\uparrow }\). Let \(N_1<N_2<\cdots N_J\leqslant N\) be the unique values such that
(For example, if \(x_1<x_2<\cdots <x_N\), then we have \(J=N-1\), with \(N_1=2\), \(N_2=3\), \(\cdots ,N_J=N\)). Let \({\overline{\alpha }}:=\min \{x_{N_j}-x_{N_j-1}\); \(j\in [1\ldots J]\}\); then, \({\overline{\alpha }}>0\). Fix \(\alpha >0\). If the axiom holds for \(\alpha \), then it holds for any \(\alpha '>\alpha \) (by Pareto). Thus, we can assume that \(\alpha <{\overline{\alpha }}\) without loss of generality. Let \({\overline{\beta }}:={\overline{\alpha }}-\alpha \); then, \({\overline{\beta }}>0\). For any \(n\in [1\ldots N]\), let
Then \(M_n>0\) because \(\phi _1,\ldots ,\phi _N\) are all strictly increasing. Let \(M:=\min \{M_1,\ldots ,M_N\}\). For all \(n\in [1\ldots N]\), there exists some \(\beta _n>0\) small enough that \(\phi _n(x_n)-\phi _n(x_n-\beta _n)<M\) (because \(\phi _n\) is continuous). Let \(\beta :=\min \{\alpha ,{\overline{\beta }},\beta _1,\ldots \beta _N\}\); then, \(\alpha>\beta >0\).
Let \({\mathbf {y}}\in {\mathbb {R}}^N\), let \(n\in [1\ldots N]\), and suppose \(x_n>y_n\geqslant x_n-\beta \), while \(y_m\geqslant x_m+\alpha \) for all \(m\ne n\). There are now two cases to consider:
Case 1 Suppose \(y_m<x_m+{\overline{\alpha }}\) for all \(m\ne n\). Then for all \(j\in [1\ldots J]\), all \(n<N_j\), and all \(m\geqslant N_j\), we have \(y_n<y_m\). Thus, by permuting the coordinates internally within each of the blocks \([1\ldots N_1)\), \([N_1\ldots N_2)\), \([N_2\ldots N_3)\), \(\cdots \), \([N_J\ldots N)\) (which does not change \({\mathbf {x}}\), by definition of \(N_1,\ldots , N_J\)), we can assume without loss of generality that \(y_1\leqslant y_2\leqslant \cdots \leqslant y_N\), so that \({\mathbf {y}}^\uparrow ={\mathbf {y}}\). Furthermore,
Rearranging this inequality, we get \(W({\mathbf {y}})\geqslant W({\mathbf {x}})\), and thus, \({\mathbf {y}}\succeq _* {\mathbf {x}}\), as desired.
Case 2 Suppose \(y_m\geqslant x_m+{\overline{\alpha }}\) for some \(m\ne n\). Define \({\mathbf {z}}\) by setting \(z_n:=y_n\) and \(z_m:=\min \{y_m,x_m+\alpha \}\) for all \(m\ne n\). Then \(y_m\geqslant z_m\) for all \(m\in [1\ldots N]\). Thus, \(y^\uparrow _m\geqslant z^\uparrow _m\) for all \(m\in [1\ldots N]\), so \({\mathbf {y}}^\uparrow \succeq _*{\mathbf {z}}^\uparrow \) by the Pareto axiom. Meanwhile, \({\mathbf {z}}\) satisfies Case 1 (because \(\alpha <{\overline{\alpha }}\)), so \({\mathbf {z}}^\uparrow ={\mathbf {z}}\succeq _* {\mathbf {x}}\). By transitivity, we get \({\mathbf {y}}^\uparrow \succeq _*{\mathbf {x}}\), as desired.
(b) Let \(r,q\in {\mathbb {R}}\) with \(r>q\). Let \(\alpha :=(r-q)/2\). By hypothesis, there is some \(A>0\) such that \(\sum _{n=N+1}^{\infty }\phi '_n(q+\alpha )=A\cdot \phi '_m(q+\alpha )\), for all \(m,N\in {\mathbb {N}}\) with \(m\leqslant N\). Since the functions \(\{\phi '_n\}_{n=1}^{\infty }\) are all nonincreasing (by concavity), this means that
Let \(\beta >0\). For any \(n\in {\mathbb {N}}\), since \(\phi _n\) is concave, we have
In particular, if \(\beta \leqslant \alpha /A\), then we can substitute inequality (B21) into inequality (B20) to obtain:
Meanwhile, if \(y\leqslant q\), then
because \(\phi '_m\) is concave. Combining inequalities (B22) and (B23) yields
for any \(x_*\geqslant q+\alpha \) and \(y\leqslant q\), and any \(m,N\in {\mathbb {N}}\) with \(m\leqslant N\).
Let \(\beta <\min \{\alpha ,\alpha /A\}\); then, \(r-\beta >q+\alpha \) (because \(\alpha =(r-q)/2\)). Let \({\mathbf {x}},{\mathbf {y}}\in {\mathcal {X}}_\propto \) with \({\mathcal {I}}({\mathbf {x}})={\mathcal {I}}({\mathbf {y}})={\mathcal {J}}\), for some finite subset \({\mathcal {J}}\subset {\mathcal {I}}\). Suppose \(i\in {\underline{\mathcal {I}}}({\mathbf {y}})\) and \(y_i\leqslant q\), and \(x_i\geqslant y_i+\alpha \), while for all other \(j\in {\mathcal {J}}\), suppose that either \(x_j= y_j\) or \(j\in {\overline{\mathcal { I}}}({\mathbf {x}})\cap {\overline{\mathcal { I}}}({\mathbf {y}})\), \(y_j\geqslant r\) and \(x_j\geqslant y_j-\beta \). In particular, this means there exists some \(y_*\geqslant r\) and \(x_*\geqslant y_*-\beta > q+\alpha \) such that \(y_j=y_*\) and \(x_j=x_*\) for all \(j\in {\overline{\mathcal { I}}}({\mathbf {x}})\cap {\overline{\mathcal { I}}}({\mathbf {y}})\). Let \(N:=\left| {\mathcal {J}}\setminus \left( {\overline{\mathcal { I}}}({\mathbf {x}})\cap {\overline{\mathcal { I}}}({\mathbf {y}})\right) \right| \); thus, in both \({\mathbf {x}}\) and \({\mathbf {y}}\), all individuals in \({\overline{\mathcal { I}}}({\mathbf {x}})\cap {\overline{\mathcal { I}}}({\mathbf {y}})\) have rank at least \(N+1\) when all members of \({\mathcal {J}}\) are ordered from lowest to highest utility. Furthermore, since all these individuals have identical utility in \({\mathbf {x}}\), and have identical utility in \({\mathbf {y}}\), we can assume without loss of generality that they have the same rank in \({\mathbf {x}}\) and \({\mathbf {y}}\). For all \(j\in {\overline{\mathcal { I}}}({\mathbf {x}})\cap {\overline{\mathcal { I}}}({\mathbf {y}})\), let n(j) be the rank that we assign to j in \({\mathbf {x}}\) and \({\mathbf {y}}\); thus, \(n(j)\geqslant N+1\). Thus,
Here, \((*)\) is because \(x_*\geqslant y_*-\beta \), \((\dagger )\) is because \(n(j)\geqslant N+1\) for all \(j\in {\overline{\mathcal { I}}}({\mathbf {x}})\cap {\overline{\mathcal { I}}}({\mathbf {y}})\), \((\diamond )\) is by inequality (B24), because \(y_i\leqslant q\), and \((\ddagger )\) is because \(x_i\geqslant y_i+\alpha \).
Let \(m:=|{\underline{\mathcal {I}}}({\mathbf {y}})|\); then, \(m\leqslant N\), by the definition of N. There are now two cases.
Case 1 Suppose that \(x_i \leqslant x_j\), for all \(j\in {\mathcal {J}}\setminus {\overline{\mathcal { I}}}({\mathbf {y}})\). Thus, in outcome \({\mathbf {x}}\), individual i has rank \(m\leqslant N\) when all members of \({\mathcal {J}}\) are ordered from lowest to highest utility. In outcome \({\mathbf {y}}\), individual i would have rank at mostm, but since the bottom m individuals have identical utilities, we can assume without loss of generality that i also has rank m in \({\mathbf {y}}\). By hypothesis, we have \(x_j=y_j\) for all \(j\in {\mathcal {J}}\setminus \left( \{i\}\cup \left[ {\overline{\mathcal { I}}}({\mathbf {x}})\cap {\overline{\mathcal { I}}}({\mathbf {y}})\right] \right) \). Thus,
where \((*)\) is by inequality (B25). Thus, \({\mathbf {x}}\succeq {\mathbf {y}}\), as claimed
Case 2 Suppose that \(x_i > x_j\), for some \(j\in {\mathcal {J}}\setminus {\overline{\mathcal { I}}}({\mathbf {y}})\). In this case, define \({\mathbf {z}}\) by setting \(z_i:=\min \{x_j; \ j\in {\mathcal {J}}\setminus {\underline{\mathcal {I}}}({\mathbf {y}})\}\), while \(z_j:=x_j\) for all other \(j\in {\mathcal {I}}\). Then \({\mathbf {x}}\) Pareto dominates \({\mathbf {z}}\), so \({\mathbf {x}}^\uparrow \) Pareto dominates \({\mathbf {z}}^\uparrow \), so \({\mathbf {x}}\succeq {\mathbf {z}}\) by the Pareto axiom. Meanwhile, \({\mathbf {z}}\) satisfies Case 1, so \({\mathbf {z}}\succeq {\mathbf {y}}\). Thus, by transitivity, \({\mathbf {x}}\succeq {\mathbf {y}}\), as desired. \(\square \)
Proof of Corollary 3.5
The strategy is very similar to the proof of Proposition 2.1. The uniqueness statement follows from the uniqueness statement in Theorem 2. \(\square \)
Rights and permissions
About this article
Cite this article
Pivato, M. Rank-additive population ethics. Econ Theory 69, 861–918 (2020). https://doi.org/10.1007/s00199-019-01194-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00199-019-01194-8



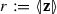 and let
and let 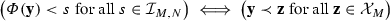 .
.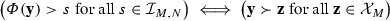 .
.