Skip to main content
SpringerLink
Log in

Differentiable classification of 4-manifolds with singular Riemannian foliations

  • Published:
Mathematische Annalen Aims and scope Submit manuscript

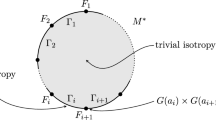
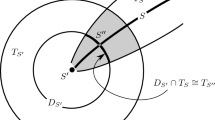
Abstract

In this paper, we first prove that any closed simply connected 4-manifold that admits a decomposition into two disk bundles of rank greater than 1 is diffeomorphic to one of the standard elliptic 4-manifolds: \(\mathbb {S}^4\), \(\mathbb {CP}^2\), \(\mathbb {S}^2\times \mathbb {S}^2\), or \(\mathbb {CP}^2\)#\(\pm \mathbb {CP}^2\). As an application we prove that any closed simply connected 4-manifold admitting a nontrivial singular Riemannian foliation is diffeomorphic to a connected sum of copies of standard \(\mathbb {S}^4\), \(\pm \mathbb {CP}^2\) and \(\mathbb {S}^2\times \mathbb {S}^2\). A classification of singular Riemannian foliations of codimension 1 on all closed simply connected 4-manifolds is obtained as a byproduct. In particular, there are exactly 3 non-homogeneous singular Riemannian foliations of codimension 1, complementing the list of cohomogeneity one 4-manifolds.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. Throughout this paper, all manifolds considered are connected and smooth.

  2. Here we ignore the specific orientations and identify \(L(\pm m,1)\).

  3. Here orientability refers to that of the total space.

  4. In [44] the second case in \(\mathbb {CP}^2\) was missing, as remarked also in [26, 32]. Note also that it should be \(\mathbb {CP}^2\)#\(-\mathbb {CP}^2\) other than \(\mathbb {CP}^2\)#\(\mathbb {CP}^2\), as the covering space of the manifolds \(43\) and \(49\) in Parker’s list.

References

  1. Adem, A., Leida, J., Ruan, Y.: Orbifolds and stringy topology. In: Cambridge Tracts in Mathematics, vol. 171. Cambridge University Press, Cambridge (2007)

  2. Akhmedov, A., Doug, B.: Park, Exotic smooth structures on small \(4\)-manifolds with odd signatures. Invent. Math. 181(3), 483–492 (2010)

    Google Scholar 

  3. Alexandrino, M.M.: Desingularization of singular Riemannian foliation. Geom. Dedicata 149, 397–416 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  4. Alexandrino, M.M., Briquet, R., Töben, D.: Progress in the theory of singular Riemannian foliations. Differ. Geom Appl. 31(2), 248–267 (2013)

    Article  MATH  Google Scholar 

  5. Alexandrino, M.M., Lytchak, A.: On smoothness of isometries between orbit spaces. Riemannian geometry and applications-Proceedings RIGA 2011, 17–28. Ed. Univ. Bucureşti, Bucharest (2011)

  6. Alexandrino, M.M., Töben, D.: Equifocality of a singular riemannian foliation. Proc. Am. Math. Soc. 136, 3271–3280 (2008)

    Article  MATH  Google Scholar 

  7. Cerf, J.: Sur les difféomorphismes de la sphère de dimension trois (\(\Gamma _4=0\)). In: Lecture Notes in Mathematics, vol. 53. Springer, Berlin (1968)

  8. Donaldson, S.K.: An application of gauge theory to four-dimensional topology. J. Differ. Geom. 18, 279–315 (1983)

    MATH  MathSciNet  Google Scholar 

  9. Donaldson, S.K.: Irrationality and the h-cobordism conjecture. J. Differ. Geom. 26, 141–168 (1987)

    MATH  MathSciNet  Google Scholar 

  10. Duan, H.B.: A generalization of the Wang sequence. Homol. Homotopy Appl. 13, 37–42 (2011)

    Article  MATH  Google Scholar 

  11. Fintushel, R.: Circle actions on simply connected \(4\)-manifolds. Trans. Am. Math. Soc. 230, 147–171 (1977)

    MATH  MathSciNet  Google Scholar 

  12. Fintushel, R.: Classification of circle actions on \(4\)-manifolds. Trans. Am. Math. Soc. 242, 377–390 (1978)

    MATH  MathSciNet  Google Scholar 

  13. Fintushel, R., Stern, R.J.: Double node neighborhoods and families of simply connected \(4\)-manifolds with \(b^{+}=1\). J. Amer. Math. Soc. 19, 171–180 (2005)

    Article  MathSciNet  Google Scholar 

  14. Freedman, M.H.: The topology of four dimensional manifolds. J. Differ. Geom. 17(3), 357–453 (1982)

    MATH  Google Scholar 

  15. Freedman, M., Quinn, F.: Topology of \(4\)-manifolds. In: Princeton Mathematical Series, vol. 39. Princeton University Press, Princeton (1990)

  16. Galaz-Garcia, F., Radeschi, M.: Singular Riemannian foliations and applications to positive and nonnegative curvature (preprint, 2013). arXiv:1302.4593

  17. Ge, J.Q.: DDVV-type inequality for skew-symmetric matrices and Simons-type inequality for Riemannian submersions. Adv. Math. 251, 62–86 (2014)

    Article  MATH  MathSciNet  Google Scholar 

  18. Ge, J.Q., Tang, Z.Z.: Isoparametric functions and exotic spheres. J. Reine Angew. Math. 683, 161–180 (2013)

    MATH  MathSciNet  Google Scholar 

  19. Ge, J.Q., Tang, Z.Z.: Geometry of isoparametric hypersurfaces in Riemannian manifolds. Asian J. Math. 18, 117–126 (2014)

    Article  MATH  MathSciNet  Google Scholar 

  20. Ge, J.Q., Tang, Z.Z., Yan, W.J.: A filtration for isoparametric hypersurfaces in Riemannian manifolds. J. Math. Soc. Jpn. (to appear, 2015). arXiv:1102.1126

  21. Ghys, E.: Feuilletages riemanniens sur les variétés simplement connexes. Ann. Inst. Fourier (Grenoble) 34, 203–223 (1984). Theorem A

  22. Gluck, H.: The embedding of two-spheres in the four-sphere. Trans. Am. Math. Soc. 104, 308–333 (1962)

    Article  MATH  MathSciNet  Google Scholar 

  23. Gompf, R.: Three exotic \(R^4\)’s and other anomalies. J. Differ. Geom. 18, 317–328 (1983)

    MATH  MathSciNet  Google Scholar 

  24. Gromoll, D., Walschap, G.: Metric foliations and curvature. In: Progress in Mathematics, vol. 268. Birkhäuser, Basel (2009)

  25. Grove, K., Halperin, S.: Dupin hypersurfaces, group actions and the double mapping cylinder. J. Differ. Geom. 26, 429–459 (1987)

    MATH  MathSciNet  Google Scholar 

  26. Grove, K., Ziller, W.: Lifting group actions and nonnegative curvature. Trans. Am. Math. Soc. 363, 2865–2890 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  27. Haefliger, A.: Holonomy Groupoïdes dholonomie et classifiants. Transversal structure of foliations (Toulouse, 1982). Astérisque 116, 70–97 (1984)

  28. Hatcher, A.E.: On the diffeomorphism group of \(\mathbb{S}^1\times \mathbb{S}^2\). Proc. Am. Math. Soc. 83, 427–430 (1981)

    MATH  MathSciNet  Google Scholar 

  29. Hatcher, A.E.: A proof of the Smale conjecture, \(Diff(\mathbb{S}^3)\simeq O(4)\). Ann. Math. 117, 553–607 (1983)

    Article  MATH  MathSciNet  Google Scholar 

  30. Hebda, J.J.: The regular focal locus. J. Differ. Geom. 16, 421–429 (1981)

    MATH  MathSciNet  Google Scholar 

  31. Hirsch, M.W.: Differential Topology (GTM. 33). Springer, New York etc. (1976)

  32. Hoelscher, C.A.: Classification of cohomogeneity one manifolds in low dimensions. Pac. J. Math. 246, 129–185 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  33. Hong, S., Kalliongis, J., McCullough, D., Rubinstein, J.H.: Diffeomorphisms of elliptic 3-manifolds. In: Lecture Notes in Mathematics, vol. 2055. Springer, Heidelberg (2012)

  34. Lawson, T.: Normal bundles for an embedded \(\mathbb{RP}^2\) in a positive definite \(4\)-manifold. J. Differ. Geom. 22, 215–231 (1985)

    MATH  Google Scholar 

  35. Lawson, T.: The minimal genus problem. Exposition. Math. 15, 385–431 (1997)

    MATH  MathSciNet  Google Scholar 

  36. Li, B.H., Li, T.J.: Minimal genus smooth embeddings in \(\mathbb{S}^2\times \mathbb{S}^2\) and \({\mathbb{CP}}^{2}\)# \(n{\overline{\mathbb{CP}^2}}\) with \(n\le 8\). Topology 37, 575–594 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  37. Lytchak, A.: Geometric resolution of singular Riemannian foliations. Geometriae Dedicata 149, 379–395 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  38. McCullough, D.: Isometries of elliptic 3-manifolds. J. London Math. Soc. 65, 167–182 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  39. Milnor, J.W., Stasheff, J.D.: Characteristic classes. Annals of Mathematics Studies, vol. 76. Princeton University, Princeton (1974)

  40. Molino, P.: Riemannian foliations. Translated from the French by Grant Cairns. With appendices by Cairns, G., Carrière, Y., Ghys, E., Salem, E., Sergiescu, V. Progress in Mathematics, vol. 73. Birkhäuser Boston Inc, Boston (1988)

  41. Montesinos, J.M.: Classical Tessellations and Three Manifolds. Universitext. Springer, Berlin (1987)

  42. Orlik, P., Raymond, F.: Actions of the torus on \(4\)-manifolds I. Trans. Am. Math. Soc. 152, 531–559 (1970)

    MATH  MathSciNet  Google Scholar 

  43. Orlik, P., Raymond, F.: Actions of the torus on \(4\)-manifolds. II. Topology 13, 89–112 (1974)

    Article  MATH  MathSciNet  Google Scholar 

  44. Parker, J.: \(4\)-dimensional G-manifolds with 3-dimensional orbits. Pac. J. Math. 125, 187–204 (1986)

    Article  MATH  Google Scholar 

  45. Qian, C., Tang, Z.Z.: Isoparametric functions on exotic spheres. Adv. Math. 272, 611–629 (2015)

    Article  MATH  MathSciNet  Google Scholar 

  46. Radeschi, M.: Low Dimensional Singular Riemannian Foliations on Spheres, Ph.D. thesis. University of Pennsylvania (2012)

  47. Steenrod, N.: The Topology of Fibre Bundles, PMS- 14. Princeton University Press, Princeton (1951)

  48. Takagi, R.: On homogeneous real hypersurfaces in a complex projective space. Osaka J. Math. 10, 495–506 (1973)

    MATH  MathSciNet  Google Scholar 

  49. Taubes, C.H.: Gauge theory on asymptotically periodic \(4\)-manifolds. J. Differ. Geom. 25, 363–430 (1987)

    MATH  MathSciNet  Google Scholar 

  50. Thorbergsson, G.: Singular Riemannian foliations and isoparametric submanifolds. Milan J. Math. 78, 355–370 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  51. Wang, Q.M.: Isoparametric Functions on Riemannian Manifolds. I. Math. Ann. 277, 639–646 (1987)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Acknowledgments

The authors are very grateful to Alexander Lytchak for kindly introducing each other, very nice suggestions and useful comments. The authors also thank Zizhou Tang, Gudlaugur Thorbergsson, Burkhard Wilking and Wolfgang Ziller for their support and valuable discussion. Many thanks also to Marcos M. Alexandrino and Fernando Galaz-Garcia for their interest and helpful conversation. The first author would like to thank the Alexander von Humboldt Foundation and the University of Cologne for their support and hospitality during his Humboldt postdoctoral position in 2012–2014, under the supervision of professor Gudlaugur Thorbergsson.

Author information

Authors and Affiliations

  1. Laboratory of Mathematics and Complex Systems, School of Mathematical Sciences, Beijing Normal University, Beijing, 100875, People’s Republic of China

    Jianquan Ge

  2. Mathematisches Institut, WWU Münster, Einsteinstr. 62, Münster, Germany

    Marco Radeschi

Authors
  1. Jianquan Ge
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Marco Radeschi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jianquan Ge.

Additional information

J. Ge is partially supported by the NSFC (No. 11001016 and No. 11331002), the SRFDP (No. 20100003120003), the Fundamental Research Funds for the Central Universities, and a research fellowship from the Alexander von Humboldt Foundation.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ge, J., Radeschi, M. Differentiable classification of 4-manifolds with singular Riemannian foliations. Math. Ann. 363, 525–548 (2015). https://doi.org/10.1007/s00208-015-1172-5

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00208-015-1172-5

Mathematics Subject Classification

Search

Navigation