Skip to main content
SpringerLink
Log in

An Algebraic Construction of Duality Functions for the Stochastic \({\mathcal{U}_q( A_n^{(1)})}\) Vertex Model and Its Degenerations

  • Published:
Communications in Mathematical Physics Aims and scope Submit manuscript

Abstract

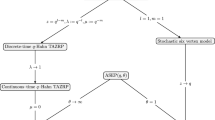
A recent paper (Kuniba in Nucl Phys B 913:248–277, 2016) introduced the stochastic \({\mathcal{U}_q(A_n^{(1)})}\) vertex model. The stochastic S-matrix is related to the R-matrix of the quantum group \({\mathcal{U}_q(A_n^{(1)})}\) by a gauge transformation. We will show that a certain function \({D^+_{\vec{m}}}\) intertwines with the transfer matrix and its space reversal. When interpreting the transfer matrix as the transition matrix of a discrete-time totally asymmetric particle system on the one-dimensional lattice \({\mathbb{Z}}\), the function \({D^+_{\vec{m}}}\) becomes a Markov duality function \({D_{\vec{m}}}\) which only depends on q and the vertical spin parameters \({\{\mu_x\}}\). By considering degenerations in the spectral parameter, the duality results also hold on a finite lattice with closed boundary conditions, and for a continuous-time degeneration. This duality function had previously appeared in a multi-species ASEP(q, j) process (Kuan in A multi-species ASEP(q, j) and q-TAZRP with stochastic duality, 2017). The proof here uses that the R-matrix intertwines with the co-product, but does not explicitly use the Yang–Baxter equation. It will also be shown that the stochastic \({\mathcal{U}_q(A_n^{(1)})}\) is a multi-species version of a stochastic vertex model studied in Borodin and Petrov (Higher spin six vertex model and symmetric rational functions, 2016) and Corwin and Petrov (Commun Math Phys 343:651–700, 2016). This will be done by generalizing the fusion process of Corwin and Petrov (2016) and showing that it matches the fusion of Kulish and yu (Lett Math Phys 5:393–403, 1981) up to the gauge transformation. We also show, by direct computation, that the multi-species q-Hahn Boson process (which arises at a special value of the spectral parameter) also satisfies duality with respect to \({D_{\infty}}\), generalizing the single-species result of Corwin (Int Math Res Not 2015:5577–5603, 2015).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Alcaraz F.C., Rittenberg V.: Reaction–diffusion processes as physical realizations of Hecke algebras. Phys. Lett. B 314(3), 377–380 (1993)

    Article  ADS  Google Scholar 

  2. Andrews, G.E., Askey, R., Roy, R.: Special Functions. vol. 71. Cambridge University Press, Cambridge (2001)

  3. Barraquand G.: A short proof of a symmetry identity for the q–Hahn distribution. Electron. Commun. Probab. 19(50), 1–3 (2014) https://doi.org/10.1214/ECP.v19-3674

    MathSciNet  MATH  Google Scholar 

  4. Barraquand G., orwin I.: The q-Hahn asymmetric exclusion process. Ann. Appl. Probab. 26(4), 2304–2356 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  5. Belitsky V., Schütz G.M.: Self-duality for the two-component asymmetric simple exclusion process. J. Math. Phys. 56, 083302 (2015) https://doi.org/10.1063/1.4929663

    Article  ADS  MathSciNet  MATH  Google Scholar 

  6. Belitsky V., Schütz G.M.: Quantum algebra symmetry and reversible measures for the ASEP with second-class particles. J. Stat. Phys. 161(4), 821–842 (2015) https://doi.org/10.1007/s10955-015-1363-1

    Article  ADS  MathSciNet  MATH  Google Scholar 

  7. Belitsky, V., Schütz, G.M.: Self-duality and shock dynamics in the n-component priority ASEP. (2016). arXiv:1606.04587v1

  8. Borodin, A., Corwin, I.: Discrete time q–TASEPs. Int. Math. Res. Not. (2013). https://dx.doi.org/10.1093/imrn/rnt206

  9. Borodin A., Corwin I., Gorin V.: Stochastic six-vertex model. Duke Math. J. 165(3), 563–624 (2016) https://doi.org/10.1215/00127094-3166843

    Article  MathSciNet  MATH  Google Scholar 

  10. Borodin A., Corwin I., Sasamoto T.: From duality to determinants for q–TASEP and ASEP. Ann. Probab. 42(6), 2314–2382 (2014) https://doi.org/10.1214/13-AOP868

    Article  MathSciNet  MATH  Google Scholar 

  11. Borodin A., Corwin I., Petrov L., Sasamoto T.: Spectral theory for the q-Boson particle system. Compos. Math. 151, 1–67 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  12. Borodin A., Petrov L.: Higher spin six vertex model and symmetric rational functions. Sel. Math. Newser. 1, 1–24 (2016)

    Google Scholar 

  13. Borodin, A., Petrov, L.: Lectures on Integrable probability: stochastic vertex models and symmetric functions. (2016). arXiv:1605.01349v1

  14. Bosnjak G., Mangazeev V.: Construction of R-matrices for symmetric tensor representations related to \({U_q(\widehat{sl_n})}\). J. Phys. A Math. Theor. 49, 495204 (2016) https://doi.org/10.1088/1751-8113/49/49/495204

    Article  MATH  Google Scholar 

  15. Cantini, L.: Asymmetric Simple Exclusion Process with open boundaries and Koornwinder polynomials. J. Phys. A Math. Gen. 37(18) (2004). arXiv:1506.00284v1

  16. Cantini, L., Garbali, A., Gier, J.D., Wheeler, M.: Koornwinder polynomials and the stationary multi-species asymmetric exclusion process with open boundaries. J. Phys. A Math. Theor. 49, 444002 (2016). https://doi.org/10.1088/1751-8113/49/44/444002

  17. Cantini, L., de Gier, J., Wheeler, M.: Matrix product and sum rule for Macdonald polynomials. (2016). arXiv:1602.04392v1

  18. Carinci, G., Giardinà, C., Redig, F., Sasamoto, T.: A generalized asymmetric exclusion process with \({\mathcal{U}_q(\mathfrak{sl}_2)}\) stochastic duality. Probab. Theory Relat. Fields. (2015). https://doi.org/10.1007/s0040-015-0674-0

  19. Carinci G., Giardinà C., Redig F., Sasamoto T.: Asymmetric stochastic transport models with \({\mathcal{U}_q(\mathfrak{su}(1,1))}\) symmetry. J. Stat. Phys. 163(2), 239–279 (2016) https://doi.org/10.1007/s10955-016-1473-4

    Article  ADS  MathSciNet  MATH  Google Scholar 

  20. Corteel S., Mandelshtam O., Williams L.: Combinatorics of the two-species ASEP and Koornwinder moments. Adv. Math. 321, 160–204 (2017) arXiv:1510.05023

    Article  MathSciNet  MATH  Google Scholar 

  21. Corwin I.: The q-Hahn Boson Process and q-Hahn TASEP. Int. Math. Res. Not. 2015(14), 5577–5603 (2015) https://doi.org/10.1093/imrn/rnu094

    Article  MathSciNet  MATH  Google Scholar 

  22. Corwin I., Petrov L.: Stochastic higher spin vertex models on the line. Commun. Math. Phys. 343(2), 651–700 (2016) https://doi.org/10.1007/s00220-015-2479-5

    Article  ADS  MathSciNet  MATH  Google Scholar 

  23. Corwin, I., Shen, H., Tsai, L.-C.: ASEP(q,j) converges to the KPZ equation. (2016). arXiv:1602.01908v1

  24. Crampe, N., Finn, C., Ragoucy, E., Vanicat, M.: Integrable boundary conditions for multi-species ASEP. J. Phys. A Math. Theor. (2016). https://doi.org/10.1088/1751-8113/49/37/375201

  25. Fuchs J.: Affine Lie Algebras and Quantum Groups. Cambridge University Press, Cambridge (1995)

    MATH  Google Scholar 

  26. Giardinà C., Kurchan J., Redig F., Vafayi K.: Duality and hidden symmetries in interacting particle systems. J. Stat. Phys. 135, 25–55 (2009) https://doi.org/10.1007/s10955-009-9716-2

    Article  ADS  MathSciNet  MATH  Google Scholar 

  27. Giardinà C., Redig F., Vafayi K.: Correlation inequalities for interacting particle systems with duality. J. Stat. Phys. 141, 242–263 (2010) https://doi.org/10.1007/s10955-010-0055-0

    Article  ADS  MathSciNet  MATH  Google Scholar 

  28. Gwa L–H., Spohn H.: Bethe solution for the dynamical-scaling exponent of the noisy Burgers equation. Phys. Rev. A. 46, 844–854 (1992)

    Article  ADS  Google Scholar 

  29. Imamura T., Sasamoto T.: Current moments of 1D ASEP by duality. J. Stat. Phys. 142(5), 919–930 (2011) https://doi.org/10.1007/s10955-011-0149-3

    Article  ADS  MathSciNet  MATH  Google Scholar 

  30. Jansen S., Kurt N.: On the notion(s) of duality for Markov processes. Probab. Surv. 11, 59–120 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  31. Karimipour, V.: A multi-species asymmetric exclusion process, steady state and correlation functions on a periodic lattice. EPL (Europhys. Lett.) (1999). https://doi.org/10.1209/epl/i1999-00389-2

  32. Kemeny J.G., Snell J.L.: Finite Markov Chains. Springer, Berlin (1976)

    MATH  Google Scholar 

  33. Kuan J.: Stochastic duality of ASEP with two particle types via symmetry of quantum groups of rank two. J. Phys A. 49(11), 29 (2016) https://doi.org/10.1088/1751-8113/49/11/115002

    Article  MathSciNet  MATH  Google Scholar 

  34. Kuan, J.: A multi-species ASEP(q,j) and q-TAZRP with stochastic duality (2017). arXiv:1605.00691v1 (to appear in Int. Mat. Res. Not.)

  35. Kulish P.P., Reshetikhin N.Yu., Sklyanin E.K.: Yang–Baxter equation and representation theory: I. Lett. Math. Phys. 5, 393–403 (1981)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  36. Kuniba, K., Mangazeev, V., Maruyama, M.: Stochastic R Matrix for U q (A (1) n ). Nucl. Phys. B 913, 248–277 (2016). arXiv:1604.08304v4

  37. Kuniba, A., Okado, M.: Matrix product formula for \({\mathcal{U}_q(A_2^{(1)})}\)-zero range process. J. Phys. A Math. Theor. 50, 4 (2016). arXiv:1608.02779v1

  38. Kuniba A., Okado M.: A q-boson representation of Zamolodchikov–Faddeev algebra for stochastic R matrix of U q (A (1) n ). Lett. Math. Phys. 107, 1111 (2017) arXiv:1610.00531v1

    Article  ADS  MathSciNet  MATH  Google Scholar 

  39. Kuniba A., Okado M., Sergeev S.: Tetrahedron equation and generalized quantum groups. J. Phys. A Math. Theor. 48, 304001 (2015) https://doi.org/10.1088/1751-8113/48/30/304001

    Article  MathSciNet  MATH  Google Scholar 

  40. Liggett T.M.: Coupling the simple exclusion process. Ann. Probab. 4, 339–356 (1976) https://doi.org/10.1214/aop/1176996084

    Article  MathSciNet  MATH  Google Scholar 

  41. Liggett T.M.: Interacting Particle Systems. Springer, Berlin (2005)

    Book  MATH  Google Scholar 

  42. Lusztig G.: Introduction to Quantum Groups. Birkhäuser, Boston (1993)

    MATH  Google Scholar 

  43. Mandelshtam, O.: Matrix ansatz and combinatorics of the k-species PASEP. (2015). arXiv:1508.04115v1

  44. Mandelshtam, O., Viennot, X.: Tableaux combinatorics of the two-species PASEP. (2015). arXiv:1506.01980v1

  45. Ohkubo, J.: On dualities for SSEP and ASEP with open boundary conditions J. Phys. A Math. Theor. 50 095004 (2017). arXiv:1606.05447v1

  46. Pitman J.W., Rogers L.C.G.: Markov functions. Ann. Probab. 9(4), 573–582 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  47. Povolotsky, A.M.: On the integrability of zero-range chipping models with factorized steady states. J. Phys. A Math. Theor. (2013). https://doi.org/10.1088/1751-8113/46/46/465205

  48. Povolotsky A.M., Priezzhev V.B.: Determinant solution for the totally asymmetric exclusion process with parallel update. J. Stat. Mech. 07, P07002 (2006) https://doi.org/10.1088/1742-5468/2006/07/P07002

    Google Scholar 

  49. Prolhac S., Evans M.R., Mallick K.: Matrix product solution of the multispecies partially asymmetric exclusion process. J. Phys. A Math. Theor. 42, 165004 (2009) https://doi.org/10.1088/1751-8113/42/16/165004

    Article  ADS  MathSciNet  MATH  Google Scholar 

  50. Reshetikhin, N.: Lectures on the integrability of the 6-vertex model. (2010). arXiv:1010.5031v1

  51. Sasamoto T., Wadati M.: Exact results for one-dimensional totally asymmetric diffusion models. J. Phys. A. 31(28), 6057–6071 (1998) https://doi.org/10.1088/0305-4470/31/28/019

    Article  ADS  MathSciNet  MATH  Google Scholar 

  52. Schütz G.: Duality relations for asymmetric exclusion processes. J. Stat. Phys. 86(5/6), 1265–1287 (1997) https://doi.org/10.1007/BF02183623

    Article  ADS  MathSciNet  MATH  Google Scholar 

  53. Schütz, G.: Duality relations for the periodic ASEP conditioned on a low current, to appear in from particle systems to partial differential equations III. In: Springer Proceedings in Mathematics and Statistics, vol. 162 (2016). arXiv:1508.03158v1

  54. Schütz G., Sandow S.: Non-Abelian symmetries of stochastic processes: Derivation of correlation functions for random-vertex models and disordered-interacting-particle systems. Phys. Rev. E 49, 2726 (1994) https://doi.org/10.1103/PhysRevE.49.2726

    Article  ADS  Google Scholar 

  55. Spitzer F.: Interaction of Markov processes. Adv. Math 5, 246–290 (1970) https://doi.org/10.1016/0001-8708(70)90034-4

    Article  MathSciNet  MATH  Google Scholar 

  56. Takeyama Y., A deformation of affine Hecke algebra and integrable stochastic particle system. J. Phys. A. (2014). https://doi.org/10.1088/1751-8113/47/46/465203

  57. Takeyama, Y.: Algebraic construction of multi-species q-Boson system. (2015). arXiv:1507.02033

  58. Uchiyama M.: Two-species asymmetric simple exclusion process with open boundaries. Chaos Solitons Fractals 35(2), 398–407 (2008) https://doi.org/10.1016/j.chaos.2006.05.013

    Article  ADS  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Columbia University, New York, NY, USA

    Jeffrey Kuan

Authors
  1. Jeffrey Kuan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jeffrey Kuan.

Additional information

Communicated by A. Borodin

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kuan, J. An Algebraic Construction of Duality Functions for the Stochastic \({\mathcal{U}_q( A_n^{(1)})}\) Vertex Model and Its Degenerations. Commun. Math. Phys. 359, 121–187 (2018). https://doi.org/10.1007/s00220-018-3108-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00220-018-3108-x

Search

Navigation