Abstract
We consider the semi-classical (or Gutzwiller–Voros) zeta functions for \(C^\infty \) contact Anosov flows. Analyzing the spectra of the generators of some transfer operators associated to the flow, we prove that, for arbitrarily small \(\tau >0\), its zeros are contained in the union of the \(\tau \)-neighborhood of the imaginary axis, \(|\mathfrak {R}(s)|<\tau \), and the half-plane \(\mathfrak {R}(s)<-\chi _0+\tau \), up to finitely many exceptions, where \(\chi _0>0\) is the hyperbolicity exponent of the flow. Further we show that the density of the zeros along the imaginary axis satisfy an analogue of the Weyl law.




Similar content being viewed by others
Notes
The line integral on the right-hand side may change its value by an integer multiple of \(2\pi i\) when we consider a different path for integration. But this ambiguity is cancelled when it is put in the exponential function and therefore the factor \(\exp (\cdot )\) on the right-hand side is well-defined.
This is the Jacobian matrix of the Poincaré map for the orbit \(\gamma \) at the intersection.
For the case of a surface with constant negative curvature (\(\equiv -1\)), the eigenvalues of \(D_\gamma \) are \(\exp (\pm |\gamma |)\). Hence we can check the equality \(Z_{sc}(s)=Z(s+1/2)\) by simple calculation.
Since the factor \(|\det (\mathrm {Id}-D^m_\gamma )|\) in the definition of \(Z_{sc}(s)\) is positive and proportional to \(|\det (Df^{m|\gamma |}|_{E_u}(x_\gamma ))|\) for \(x_\gamma \in \gamma \), the sum in the definition of \(Z_{sc}(s)\) converges absolutely if and only if (1.5) holds (see [29, Theorem C] for the definition of topological pressure \(P_{top}(\cdot )\) and its expression in terms of periodic orbits in the case of Anosov flow.) Further \(Z_{sc}(s)\) has its rightmost zero at \(P_{top}(f^t, -(1/2)\log |Df^t|_{E_u}|)\). For the proof, see [37] and the expression (1.13).
The number of exceptional zeros may increase as \(\tau \) becomes smaller.
We always assume that each vector bundle is complexified and equipped with a Hermitian inner product on it. The choice of the Hermitian inner product is not essential. But we need it for some expressions, e.g. the definition (1.11).
As careful readers may have realized, the sub-bundles \(E_u\) (and \(E_s\)) are not smooth in general and this will cause many technical difficulties in the argument. Indeed this is the main issue of this paper in technical sense. We will address this problem in the next section. For a while, we assume that \(E_u\) is smooth or just ignore the problem.
The lower bound \(+0\) in the integration indicates some small positive number that is smaller than the minimum of the periods of periodic orbits for the flow.
We can and do take the constant \(\chi _0\) same as that in (1.3), though this is not necessary.
But note that the rigorous argument in the proofs will somewhat deviate from the explanation here by technical reasons.
In terminology of dynamical system theory, this is nothing but the non-wandering set for the dynamics of \((Df_G^{-t})^*\).
Here we do not explain why we apply this smoothing along stable foliation. Let us just note that the effect of this smoothing will decreases exponentially fast in further evolution.
For simplicity, we assume that the stable and unstable subbundle are orientable and f preserves their orientations.
We will take flow-box coordinate charts \(\kappa \) and \(\kappa '\) around a point P and its image \(f^{t_0}_G(P)\) respectively, so that the q-axis and p-axis corresponds to the unstable and stable subspace, and consider the family of maps \((\kappa ')^{-1}\circ f^{t+t_0}_G\circ \kappa \). Then its linearization will look like \(B^t\).
Notice that this function \(\mathcal {W}^r\) is continuous despite of the discontinuity of the coordinates \((\zeta _p,\tilde{\xi }_y,\zeta _q, \tilde{y})\) at points on the hyperplane \(\xi _z=0\).
This definition of \(\chi (\cdot )\) may look a bit strange for the argument below. Since we use this function \(\chi (\cdot )\) later in a different context, we define it in this way.
In terms of the theory of pseudo-differential operator, this implies that the function \(\mathfrak {W}^r\) does not belong to an appropriate class of symbols.
We consider the condition \(|\omega |\geqslant 3\) below from Remark 4.11.
We learned the following argument from the paper [39] of Sjöstrand.
By the Riemann mapping theorem, we find a biholomorphic mapping which maps the region \(\widetilde{R}(\omega _*)\) onto the unit disk \(|z|<1\) so that a point \(s_*\in \widetilde{R}(\omega _*)\) with \(\mathrm {Re}(s_*)>C_1\) and \(\mathrm {Im}(s_*)=\omega _*\) is sent to the origin 0. Then we apply Jensen’s formula to the holomorphic function on the unit disk corresponding to k(s) (see also the proof of Corollary 8.8).
We suppose that subharmonic functions can take value \(-\infty \) and that \(\log 0=-\infty \).
Note that \(e^{x}/(1+x)>1\) for \(x>-1\).
As we noted in Remark 8.5, we actually have proved discreteness of the spectral set of the generator A only on the region \(\mathrm {Re}(s)>-\chi _0+\tau \) and \(|\mathrm {Im}(s)|\geqslant s_0\) for some large \(s_0\). We will see that this is true for the region \(\mathrm {Re}(s)>-r\chi _0/4\) in Appendix 1.
We do not need the estimate on \(\Vert A_{3,1}\Vert \) as it is determined by \(x_0\) and \(A_{1,1}\).
We refer [23, Chapter IV, Section 7] for Hilbert–Schmidt operators.
Here and a few lines below, we mean by “almost orthogonal” that we have the estimate corresponding to (8.18).
If \(\mathbf {L}_{\mathbf {j}\rightarrow \mathbf {j}}\) is a trace class operator, it is expressed as \(\mathbf {L}_{\mathbf {j}\rightarrow \mathbf {j}}=\sum _{k} v_k\otimes v_k^*\) with \(v_k\in \mathbf {K}^r_{\mathbf {j}}\), \(v_k^*\in (\mathbf {K}^r_{\mathbf {j}})^*\) satisfying \(\sum _k \Vert v_k\Vert _{\mathbf {K}^r_{\mathbf {j}}}\Vert v_k^*\Vert _{(\mathbf {K}^r_{\mathbf {j}})^*}<\infty \). Then the Schwartz kernel of \(\mathbf {L}_{\mathbf {j}\rightarrow \mathbf {j}}\) is \(\sum _k v_k\otimes v_k^*\) and the flat trace equals \(\sum _k (v_k)^* v_k=\mathrm {Tr}\mathbf {L}_{\mathbf {j}\rightarrow \mathbf {j}}\).
Actually we proved this for \(s\in [t_0,2t_0]\). But it is easy to see that the estimates remain true for \([t_0,2t_0+2]\).
Note that the variable \(\omega \in \mathbb {Z}\) does not indicate the frequency as in the previous sections but the range of time, now and henceforth.
References
Aebischer, B., Borer, M., Kälin, M., Leuenberger, Ch., Reimann, H.M.: Symplectic Geometry, Progress in Mathematics, vol. 124. Birkhäuser, Basel (1994)
Ahlfors, L.V.: Complex Analysis. An introduction to the theory of analytic functions of one complex variable, International Series in Pure and Applied Mathematics, 3rd edn. McGraw-Hill Book Co., New York (1978)
Baladi, V.: Anisotropic Sobolev spaces and dynamical transfer operators: \(C^\infty \) foliations, In: Kolyada, S., Manin, Y., Ward, T. (eds.) Algebraic and topological dynamics. vol. 385, pp. 123–135. Contemporary Mathematics, Providence, RI (2005)
Baladi, V., Tsujii, M.: Anisotropic Hölder and Sobolev spaces for hyperbolic diffeomorphisms. Ann. Inst. Fourier (Grenoble) 57(1), 127–154 (2007)
Baladi, V., Tsujii, Masato.: Dynamical determinants and spectrum for hyperbolic diffeomorphisms. In: Geometric and probabilistic structures in dynamics, Contemporary Mathematics. vol. 469, pp. 29–68. American Mathematical Society, Providence (2008)
Cvitanović, P., Rosenqvist, P.E., Vattay, G., Rugh, H.H.: A Fredholm determinant for semiclassical quantization. Chaos 3(4), 619–636 (1993)
Cvitanović, P., Vattay, G.: Entire Fredholm determinants for evaluation of semiclassical and thermodynamical spectra. Phys. Rev. Lett. 71(25), 4138–4141 (1993)
Datchev, K., Dyatlov, S., Zworski, M.: Sharp polynomial bounds on the number of Pollicott–Ruelle resonances. Ergodic Theory Dyn. Syst. 34(4), 1168–1183 (2014)
Dolgopyat, D.: On decay of correlations in Anosov flows. Ann. Math. (2) 147(2), 357–390 (1998)
Dyatlov, S.: Resonance projectors and asymptotics for \(r\)-normally hyperbolic trapped sets. J. Am. Math. Soc. 28(2), 311–381 (2015)
Dyatlov, S., Zworski, M.: Dynamical zeta functions for Anosov flows via microlocal analysis. Ann. Sci. École Norm. Sup. 49, 543–577 (2016)
Dyatlov, S., Zworski, M.: Ruelle zeta function at zero for surfaces (2016). arXiv:1606.04569
Faure, F.: Prequantum chaos: resonances of the prequantum cat map. J. Mod. Dyn. 1(2), 255–285 (2007)
Faure, F., Roy, N., Sjöstrand, J.: Semi-classical approach for Anosov diffeomorphisms and Ruelle resonances. Open Math. J. 1, 35–81 (2008)
Faure, F., Sjöstrand, J.: Upper bound on the density of Ruelle resonances for Anosov flows. Commun. Math. Phys. 308(2), 325–364 (2011)
Faure, F., Tsujii, M.: Band structure of the Ruelle spectrum of contact Anosov flows. C. R. Math. Acad. Sci. Paris 351(9–10), 385–391 (2013)
Faure, F., Tsujii, M.: Band structure of the spectrum of contact anosov flows (In preparation)
Faure, F., Tsujii, M.: Prequantum transfer operator for symplectic Anosov diffeomorphism. Astérisque 375, ix+222 (2015)
Gerald, B.: Folland, Harmonic Analysis in Phase Space. Annals of Mathematics Studies, vol. 122. Princeton University Press, Princeton, NJ (1989)
Fried, D.: The zeta functions of Ruelle and Selberg. I. Ann. Sci. École Norm. Sup. (4) 19(4), 491–517 (1986)
Fried, D.: Torsion and closed geodesics on complex hyperbolic manifolds. Invent. Math. 91(1), 31–51 (1988)
Giulietti, P., Liverani, C., Pollicott, M.: Anosov flows and dynamical zeta functions. Ann. Math. (2) 178(2), 687–773 (2013)
Gohberg, I., Goldberg, S., Krupnik, N.: Traces and Determinants of Linear Operators. Operator Theory: Advances and Applications, vol. 116. Birkhäuser, Basel (2000)
Gouëzel, S., Liverani, C.: Compact locally maximal hyperbolic sets for smooth maps: fine statistical properties. J. Differ. Geom. 79(3), 433–477 (2008)
Guillemin, V.: Lectures on spectral theory of elliptic operators. Duke Math. J. 44(3), 485–517 (1977)
Gutzwiller, M.C.: Chaos in Classical and Quantum Mechanics. Interdisciplinary Applied Mathematics, vol. 1. Springer, New York (1990)
Hörmander, L.: The Analysis of Linear Partial Differential Operators. I. Classics in Mathematics. Springer, Berlin (2003)
Juhl, A.: Cohomological Theory of Dynamical Zeta Functions. Progress in Mathematics, vol. 194. Birkhäuser Verlag, Basel (2001)
Lu, Z.-H.: Topological pressure of continuous flows without fixed points. J. Math. Anal. Appl. 311(2), 703–714 (2005)
Martinez, A.: An Introduction to Semiclassical and Microlocal Analysis. Universitext. Springer, New York (2002)
McKean, H.P.: Selberg’s trace formula as applied to a compact Riemann surface. Commun. Pure Appl. Math. 25, 225–246 (1972)
Morita, T.: Meromorphic extensions of a class of dynamical zeta functions and their special values at the origin. Ergod. Theory Dyn. Syst. 26(4), 1127–1158 (2006)
Nagel, R.: One-Parameter Semigroups for Linear Evolution Equations, vol. 194. Springer, New York (2000)
Rodino, L., Nicola, F.: Global Pseudo-Differential Calculus on Euclidean Spaces. Pseudo-Differential Operators. Birkhauser, New York (2010)
Nonnenmacher, S., Zworski, M.: Decay of correlations for normally hyperbolic trapping. Invent. Math. 200(2), 345–438 (2015)
Parry, W., Pollicott, M.: Zeta functions and the periodic orbit structure of hyperbolic dynamics. Astérisque 187–188, 268 (1990)
Ruelle, D.: Generalized zeta-functions for Axiom A basic sets. Bull. Am. Math. Soc. 82(1), 153–156 (1976)
Selberg, A.: Harmonic analysis and discontinuous groups in weakly symmetric Riemannian spaces with applications to Dirichlet series. J. Indian Math. Soc. (N.S.) 20, 47–87 (1956)
Sjöstrand, J.: Asymptotic distribution of eigenfrequencies for damped wave equations. Publ. Res. Inst. Math. Sci. 36(5), 573–611 (2000)
Smale, S.: Differentiable dynamical systems. Bull. Am. Math. Soc. 73, 747–817 (1967)
Sunada, T.: Fundamental Groups and Laplacians. Geometry and Analysis on Manifolds (Katata/Kyoto: Lecture Notes in Math., vol. 1339. Springer, Berlin 1988, pp. 248–277 (1987)
Tsujii, M.: Quasi-compactness of transfer operators for contact Anosov flows. Nonlinearity 23, 1495–1545 (2010)
Tsujii, M.: Contact anosov flows and the Fourier–Bros–Iagolnitzer transform. Ergod. Theory Dyn. Syst. 32(6), 2083–2118 (2012)
Voros, A.: Spectral functions, special functions and the Selberg zeta function. Commun. Math. Phys. 110(3), 439–465 (1987)
Voros, A.: Unstable periodic orbits and semiclassical quantisation. J. Phys. A: Math. Gen. 21(3), 685 (1988)
Author information
Authors and Affiliations
Corresponding author
Additional information
The authors thank Colin Guillarmou and Semyon Dyatlov for helpful discussions and useful comments during they are writing this paper. They also thank the anonymous referee for many (indeed more than 100!) comments to the previous version of this paper based on very precise reading, which was indispensable in correcting errors and making the paper more readable. F. Faure thanks the ANR agency support ANR-09-JCJC-0099-01. M. Tsujii thanks the support by JSPS KAKENHI Grant Number 22340035.
Appendices
Appendix A. Proof of Lemma 11.15
As we noted in the text after the statement of Lemma 11.15, the proof is obtained by elementary geometric estimates about diffeomorphisms with some hyperbolicity. We begin with preliminary argument. For definiteness, we assume that
- (\(\bigstar 1\)):
-
the condition (ii) in (7.7) holds, that is, \(t\geqslant t_0\), and
- (\(\bigstar 2\)):
-
the condition (10.17) holds.
The cases where these conditions do not hold are treated in a parallel and simpler manner. (See Remark A.2.) Further we may and do assume
- (\(\bigstar 3\)):
-
\(\min \{\max \{e^{|m(\mathbf {j})|}, \langle \omega (\mathbf {j})\rangle \}, \max \{e^{|m(\mathbf {j}')|}, \langle \omega (\mathbf {j}')\rangle \}\}\) is large, and
- (\(\bigstar 4\)):
-
\(e^{\chi _{\max }\cdot 2t(\omega )}\leqslant \langle \omega \rangle ^{\theta /10}\)
by choosing large constant \(k_0\) in the definition of the low-frequency part and small constant \(\epsilon _0>0\) in the definition of \(t(\omega )\) in (7.1) respectively.
For simplicity, we set \( \omega =\omega (\mathbf {j})\), \(\omega '=\omega (\mathbf {j}')\), \(m=m(\mathbf {j})\), \(m'=m(\mathbf {j}')\). Below we consider points
and estimate the quantity (10.25). By changing the coordinates by a transformation in \(\mathcal {A} _2\), we may and do assume
- (\(\bigstar 5\)):
-
\(\mathfrak {p}_{(x,z)}(w'')=0\) and \(\mathfrak {p}_{(x,z)}((\breve{f}^t_{\mathbf {j}\rightarrow \mathbf {j}'})^{-1}(w''))=0\)
without loss of generality. From the assumption that \(\mathbf {L}^{t,\sigma \rightarrow \sigma '}_{\mathbf {j}\rightarrow \mathbf {j}'}\) is a component of \(\mathbf {L}^{t,\sigma \rightarrow \sigma '}_{\mathrm {hyp},\not \hookrightarrow }\), we have \(m\cdot m'\ne 0\) and hence
We can get the conclusion of the lemma for small \(\gamma _0\) easily by using (A.4) if either
Therefore we will assume
- (\(\bigstar 6\)):
-
\(\max \{\;\langle \omega '\rangle ^{1/2}|w'-w''|, \; \langle \omega \rangle ^{1/2}|w-(\breve{f}^t_{\mathbf {j}\rightarrow \mathbf {j}'})^{-1}(w'')|\;\}< e^{\max \{|m|,|m'|\}/3}\).
We prove the following claim under the additional assumptions above.
Sublemma A.1
There exists a constant \(C_0>0\) such that
where \(D^*E_{\omega ,m}\) is the linear map defined in (6.8).
We defer the proof of this sublemma for a while and finish the proof of Lemma 11.15. We show that w-component of the quantity on the left hand side of (A.5), i.e. \(E_{\omega ,m}(\breve{f}^t_{\mathbf {j}\rightarrow \mathbf {j}'}(w)-w')\), is much smaller than the right-hand side of (A.5). In the case \(|m|\leqslant n_1(\omega )\), we have \(D^*E_{\omega ,m}=\mathrm {Id}\) and \(|\breve{f}^t_{\mathbf {j}\rightarrow \mathbf {j}'}(w)-w'|\) is much smaller than the right-hand side of (A.5) from (\(\bigstar 4\)), (\(\bigstar 5\)), (\(\bigstar 6\)) and (A.4). In the case \(|m|> n_1(\omega )\), we have \(e^{|m|}\geqslant C_0^{-1}\langle \omega \rangle ^{\Theta _1}\) and hence
is again much smaller than the right-hand side of (A.5).
Comparing Sublemma A.1 with what we proved in the last paragraph, we see
To finish, we prove
for a small constant \(\gamma _0>0\). Clearly the required estimate in Lemma 11.15 follows from this claim. In the case \(\langle \omega \rangle ^{1/2-4\theta } |\xi _w|\leqslant 2\), we may neglect the second factor on the left hand side and hence obtain (A.7) immediately using (A.4) and (A.6). Thus we consider the case \(\langle \omega \rangle ^{1/2-4\theta } |\xi _w|> 2\) below. In this case, we have
from (A.2), (\(\bigstar 5\)) and (\(\bigstar 6\)). Hence it holds
and the left-hand side of (A.7) is bounded from below by
Since \(e_\omega (|m|)\leqslant e^{\mu \max \{|m|,|m'|\}}\leqslant e^{\max \{|m|,|m'|\}/20}\), we obtain (A.7) again.
Proof of Sublemma A.1
For the points \(\mathbf {p}\) and \(\mathbf {p}'\) in (A.2) and (A.3), we set
and also set
The claim of Sublemma A.1 follows if we prove
Here we note that \(\langle \xi '_z\rangle /\langle \xi _z\rangle \) is bounded because of the assumption (\(\bigstar 2\)).
For the proof of (A.11), we investigate the conditions on the points (A.8) and (A.9) that come from the choice (A.2) and (A.3) of \(\mathbf {p}\) and \(\mathbf {p}'\). Then we look into the correspondence from the point (A.8) to (A.10).
From the assumptions (\(\bigstar 5\)) and (\(\bigstar 6\)), the points \(\mathbf {p}\) and \(\mathbf {p}'\) satisfy respectively
Recall that the function \(\Psi ^{\sigma }_{\mathbf {j}}\) is defined in (6.10) using the coordinates (4.24). We let \((\zeta _q,\zeta _p,\tilde{y}, \tilde{\xi }_y)\) and \((\zeta '_q,\zeta '_p,\tilde{y}', \tilde{\xi }'_y)\) be the coordinates (4.24) for the points \(\mathbf {p}\) and \(\mathbf {p}'\) in (A.2) and (A.3) respectively. Then, from (A.12), we have
and
From the former estimate and the condition (A.2), we see that the point (A.8) satisfies the following conditions up to errors bounded by \(Ce^{\max \{|m|,|m'|\}/3}\langle \omega \rangle ^{-1/2}\): For the distance from the origin,
where we write \(\hat{\xi }_x=(\hat{\xi }_p,\hat{\xi }_q)\); For the direction from the origin,
We have the parallel estimates on the point (A.9) as a consequence of (A.3).
Next we consider the correspondence from the point (A.8) to the point (A.10). By contracting property of \(f^t_{\mathbf {j}\rightarrow \mathbf {j}'}\) along the y-axis and Lemma 10.4(1), we have
Recall the diffeomorphism \(h^t_{\mathbf {j}\rightarrow \mathbf {j}'}\) in (10.12), which is roughly the flow \(f^t_G\) viewed in the local charts without the factor \(E_{\omega ,m}\). By the relation (10.11), we have
where \(\check{w}\) is chosen so that \((\check{w},z)=E_{\omega }(w'',z)\).
To proceed, let us first consider the case where \(|m|\leqslant n_1(\omega )\) and \(|m'|\leqslant n_1(\omega ')\). In this case, we have \(e_{\omega }(m)=e_{\omega '}(m')=1\), \(E_{\omega ,m}=E_{\omega ',m'}=\mathrm {Id}\) and therefore the correspondence (A.20) is given by nothing but the map \(f^t_{\mathbf {j}\rightarrow \mathbf {j}'}\). Then, by Lemma 10.4, we get (A.11) by simple geometric estimates. Indeed, if we ignore
-
the difference between \(f^t_{\mathbf {j}\rightarrow \mathbf {j}'}\) and its linearization at the origin,
-
the errors mentioned about the estimates (A.15)–(A.18) and the corresponding estimates on \((\hat{y}',\hat{\xi }'_x,\hat{\xi }'_y)\), and
-
the difference between \(\langle \xi '_z\rangle /\langle \xi _z\rangle \) and 1,
then the conclusion (A.11) is an easy consequence of hyperbolicity of \(f^t_{\mathbf {j}\rightarrow \mathbf {j}'}\). But we can check easily that the differences above are negligible in fact.
Next we consider the case \(|m|\geqslant n_2(\omega )\) and \(|m'|\geqslant n_2(\omega ')\), the other extreme. In this case, we have \(E_{\omega ,m}=E_{\omega }\) and \(E_{\omega ',m'}=E_{\omega '}\) and therefore the correspondence (A.20) is given by the map \(h^t_{\mathbf {j}\rightarrow \mathbf {j}'}\). Note that \(h^t_{\mathbf {j}\rightarrow \mathbf {j}'}\) is given as iteration of the maps satisfying the conditions in Lemma 10.3 and therefore have nice hyperbolic property. (Note that Lemma 10.3 is valid only for \(0\leqslant t\leqslant 2t_0\).) Then we can get the conclusion (A.11) by essentially same manner as in the previous case.
The situations in the middle, i.e. the case where either \(n_1(\omega )\leqslant |m|\leqslant n_2(\omega )\) or \(n_1(\omega ')\leqslant |m'|\leqslant n_2(\omega ')\) is slightly more complicated. If \(||m|-|m'||\geqslant 2\chi _{\max } t\), it is easy to get the conclusion (A.11) because the ratio between \(e^{|m|}\) and \(e^{|m'|}\) is much larger (or smaller) than the expansion (or contraction) given by the correspondence (A.20). So we may assume \(||m|-|m'||\leqslant 2\chi _{\max } t\). If we have \(e_\omega (m)=e_{\omega '}(m')\) and \(E_{\omega ,m}=E_{\omega ',m'}\), we can see that the correspondence (A.20) has good hyperbolic property in the same manner as in the proof of Lemma 10.4 and hence we can get the conclusion (A.20) again. But, from the slowly varying property (6.7) of \(e_{\omega }(m)\), it is clear that the conclusion remains true without this assumption. \(\square \)
Remark A.2
In the case where the condition (i) in (7.7) holds and \(0\leqslant t\leqslant t_0\), we can follow the argument given in the proof above. The only difference is that, instead of the condition \(t\geqslant t_0\) that ensure enough hyperbolicity of \(f^t_{G}\), we use the fact that \(\sigma '< \sigma \) in the estimates. In the case where the condition (10.17) does not hold, the proof is much simpler. We can obtain the conclusion immediately unless both of \(|m(\mathbf {j})|\) and \(|m(\mathbf {j}')|\) satisfy \(|m(\mathbf {j})|>n_2(\omega )\) and \(|m(\mathbf {j}')|> n_2(\omega ')\). But, in such case, the conclusion is again easy to obtain as we mentioned in the proof above.
Appendix B. Proof of the main theorem (2): Theorem 2.3
In this section, we prove Theorem 2.3, using the propositions given in Sect. 10. Below we continue to consider the case \(\mathcal {L}^t=\mathcal {L}^t_{0,0}\) as in the previous sections. But we can proceed in parallel in the case of vector-valued transfer operators \(\mathcal {L}^t_{k,\ell }\) with \((k,\ell )\ne (0,0)\) by regarding them as matrices of scalar valued transfer operators, as we have noted in Remark 2.4 (See also Remark 6.9, Remark 7.15 and Remark 8.11). The argument in this section is essentially parallel to that in [5], where dynamical zeta functions for hyperbolic diffeomorphisms are considered. The main idea is to decompose the operators in consideration into two parts: a trace class part and a “upper-triangular” part whose flat trace is zero. To realize this idea, we will consider the lifted operator \(\mathbf {L}^t\) rather than \(\mathcal {L}^t\). Below we suppose that the operators are acting on \(\mathcal {K}^r(K_0)\) or \(\mathbf {K}^r\) if we do not specify otherwise.
1.1 B. 1. Analytic extension of the dynamical Fredholm determinant
The dynamical Fredholm determinant d(s) of the one-parameter group of transfer operators \(\mathbb {L}=\{\mathcal {L}^t=\mathcal {L}^t_{0,0}\}\) is well-defined if the real part of s is sufficiently large. In fact, the sum in the definition (2.6) of d(s) converges absolutely if \(\mathrm {Re}(s)\) is larger than the topological pressure \(P_{top}:=P_{top}(f^t, -(1/2)\log |\det Df^t|_{E_u}|)\) (see [29, Theorem 4.1] for instance). Hence d(s) is a holomorphic function without zeros on \(\mathrm {Re}(s)>P_{top}\). We take a constant \(P\geqslant P_{top}\) such that
and consider the function \(\log d(s)\) in the disk
for \(s_0\in \mathbb {C}\) with \(\mathrm {Re}(s_0)>P\) and \(r_0:=\mathrm {Re}(s_0)+r\chi _0/4\). The n-th coefficient of the Taylor expansion of \(\log d(s)\) at the center \(s_0\) is
Since we have
we may write the coefficient \(a_n\) as
We are going to relate the asymptotic behavior of flat trace \(\mathrm {Tr}^\flat (\mathcal {R}(s_0)^n)\) as \(n\rightarrow \infty \) with the spectrum of the generator A. Precisely we prove
Proposition B.1
The spectral set of the generator A of \(\mathcal {L}^t:{\widetilde{\mathcal {K}}}^{r}(K_0)\rightarrow {\widetilde{\mathcal {K}}}^{r}(K_0)\) in the disk \(D(s_0,r_0)\) consists of finitely many eigenvalues \(\chi _i\in \mathbb {C}\), \(1\leqslant i\leqslant m\), counted with multiplicity. We have the asymptotic formula
where the remainder term \(Q_n\) satisfies
with a constant \(C>0\) which may depend on \(s_0\).
Theorem 2.3 is an immediate consequence of this proposition. In fact, we have
and hence
for \(z\in \mathbb {C}\) with sufficiently small absolute value. The right-most factor on the right-hand side extends holomorphically to the disk \(D(s_0,r_0)\) and has no zeros on it. So the dynamical Fredholm determinant d(s) extends to the disk \(D(s_0,r_0)\) as a holomorphic function and the zeros in \(D(s_0,r_0)\) are exactly \(\chi _i\), \(1\leqslant i\leqslant m\), counted with multiplicity. Note that this conclusion holds for any \(s_0\in \mathbb {C}\) with \(\mathrm {Re}(s)>P_{top}\) so that the imaginary part of \(s_0\) is arbitrary. Therefore, taking \(r_*>0\) so large that \(r_*\chi _0/4>c\), we obtain the conclusion of Theorem 2.3.
1.2 B. 2. The flat trace of the lifted transfer operators
To proceed, we discuss about the flat trace of the lifted operators and averaging with respect to time. Suppose that \(\mathbf {L}:\mathbf {K}^{r}\rightarrow \mathbf {K}^{r}\) is a bounded operator, expressed as
If the diagonal components \(\mathbf {L}_{\mathbf {j}\rightarrow \mathbf {j}}:\mathbf {K}^{r}_{\mathbf {j}}\rightarrow \mathbf {K}^{r}_{\mathbf {j}}\) for \(\mathbf {j}\in \mathcal {J}\) are trace class operators and if the sum of their traces converges absolutely, we set
and call it the flat trace of the operator \(\mathbf {L}:\mathbf {K}^{r}\rightarrow \mathbf {K}^{r}\).
Remark B.2
In this definition, we assume that each \(\mathbf {L}_{\mathbf {j}\rightarrow \mathbf {j}}\) is a trace class operator and henceFootnote 29 that its trace coincides with the flat trace.
Definition B.3
An operator \(\mathbf {L}\) as above is upper triangular (with respect to the index \(\tilde{m}(\cdot )\)) if the components \(\mathbf {L}_{\mathbf {j}\rightarrow \mathbf {j}'}\) vanishes whenever \(\tilde{m}(\mathbf {j}') \leqslant \tilde{m}(\mathbf {j})\). (Recall (11.15) for the definition of the index \(\tilde{m}(\cdot )\).)
The next lemma is obvious from the definitions.
Lemma B.4
If \(\mathbf {L}\) is upper triangular, its flat trace vanishes. If \(\mathbf {L}\) and \(\mathbf {L}'\) are upper triangular, so are their linear combinations \(\alpha \mathbf {L}+\beta \mathbf {L}'\) and their composition \(\mathbf {L}\circ \mathbf {L}'\).
Since the flat trace of \(\mathcal {L}^t\) is a distribution as a function of t, it takes values against smooth functions \(\varphi (t)\) with compact support. Hence, rather than evaluating the flat trace of \(\mathcal {L}^t\) itself, it is natural and convenient to consider the flat trace of the integration of \(\mathcal {L}^t\),
against a smooth function \(\varphi :\mathbb {R}_+\rightarrow \mathbb {R}\) compactly supported on the positive part of the real line. We will also consider the corresponding lifted operator
Recall the decomposition of the operator \(\mathbf {L}^t\),
that we introduced in Sect. 11.
Lemma B.5
Suppose that \(\mathcal {P}\) is a set of \(C^\infty \) functions supported on \([0, 2]\subset \mathbb {R}\) and uniformly bounded in the \(C^\infty \) sense. Then there exists a constant \(C>0\) such that the following holds true: For any \(\varphi \in \mathcal {P}\), the operator \({\mathbf {L}}(\varphi )\circ \mathbf {L}^t=\mathbf {L}^t\circ {\mathbf {L}}(\varphi )\) for \(t_0\leqslant t\leqslant 2t_0\) is decomposed into two parts

The former \(\widehat{\mathbf {L}}\) is upper triangular and satisfies \(\Vert \widehat{\mathbf {L}}\Vert \leqslant C\), while the latter  is a trace class operator and satisfies
is a trace class operator and satisfies  ; Further the operator
; Further the operator
is a trace class operator and we have \(\Vert (\mathbf {L}^{t}-\mathbf {L}^{t}_{\mathrm {hyp},\hookrightarrow })\circ \mathbf {L}(\varphi )\Vert _{\mathrm {Tr}}\leqslant C\).
Proof
The part \(\widehat{\mathbf {L}}\) is upper triangular and satisfies \(\Vert \widehat{\mathbf {L}}\Vert \leqslant C\) by the definition of the relation \(\hookrightarrow ^t\) in Definition 11.11 and Proposition 11.13. From Lemma 11.18 and Proposition 11.13, we know that the operators \(\mathbf {L}_{\mathrm {low}}^{s}\) and \(\mathbf {L}^{s}_{\mathrm {hyp},\not \hookrightarrow }\) are trace class operators and their trace norms are bounded uniformly forFootnote 30 \(s\in [t_0, 2t_0+2]\). It remains to show that \(\int \varphi (s-t) \cdot \mathbf {L}^{s}_{\mathrm {ctr}} ds\) and \( \mathbf {L}^{t}_{\mathrm {ctr}}\circ \mathbf {L}(\varphi )\) are trace class operators and that their traces are uniformly bounded for \(t_0\leqslant t\leqslant 2t_0\) and \(\varphi \in \mathcal {P}\). These claims follow if we show
for \(\mathbf {j},\mathbf {j}'\in \mathcal {J}\) with \(m(\mathbf {j}')=0\) and \(t_0\leqslant t\leqslant 2t_0\). Note that, if we apply the argument in the proofs of Lemma 10.11 and Corollary 10.12 to \((\mathbf {L}(\varphi )\circ \mathbf {L}^t)_{\mathbf {j}\rightarrow \mathbf {j}'}\), we obtain the required estimate (B.6) without the term \(\langle \omega (\mathbf {j})\rangle ^{-\nu }\) on the right-hand side. To retain the term \(\langle \omega (\mathbf {j})\rangle ^{-\nu }\), we make use of the additional integration with respect to time in \(\mathbf {L}(\varphi )\). Since \(f^{t+t'}_{\mathbf {j}\rightarrow \mathbf {j}'}(w,z)=f^{t}_{\mathbf {j}\rightarrow \mathbf {j}'}(w,z)+(0,t')\) when \(|t'|\) is sufficiently small, such integration will reduce the \(\mathbf {j}'\)-components of the image with large \(\omega (\mathbf {j}')\). Indeed, if we (additionally) apply integration by parts to that integral with respect to time using the differential operator \(\mathcal {D}=(1-i\xi '_z\partial _{t})(1+|\xi '_z|^2)\) for several times, we obtain the extra factor \(\langle \omega (\mathbf {j})\rangle ^{-\nu }\). \(\square \)
Corollary B.6
If \(\varphi :[t_0, \infty )\rightarrow \mathbb {R}\) be a smooth function with compact support, we have \(\mathrm {Tr}^\flat \mathbf {L}(\varphi )=\mathrm {Tr}^\flat \mathcal {L}(\varphi )\).
Proof
From the proof of Lemma B.5 above, we see that \(\mathrm {Tr}^\flat \mathbf {L}(\varphi )\) is well-defined, that is, the sum over \(\mathbf {j}\in \mathcal {J}\) in the definition converges absolutely. Hence we obtain
by rotating the order of composition in the middle. \(\square \)
1.3 B.3. The flat trace of the iteration of the resolvent
Let us put
and
where the function \(\chi (\cdot )\) is that in (5.2).
Remark B.7
The operator \({\mathcal {R}}^{(n)}\) above is defined as an approximation of \({\mathcal {R}}(s_0)^{n}\) and the difference is
We put the part \(\widetilde{\mathcal {R}}^{(n)}\) aside because we can not treat the operators \(\mathcal {L}^t\) with small \(t>0\) in the same way as those with large \(t>0\). Since the flat trace and also the operator norm of \(\widetilde{\mathcal {R}}^{(n)}\) on \({\widetilde{\mathcal {K}}}^{r}(K_0)\) converges to zero super-exponentially fast as \(n\rightarrow \infty \), this does not cause any essential problem, though it introduces some complication in a few places below.
We take constants \(r'_0<r''_0\) such that
Lemma B.8
There exists a constant \(C>0\), independent of n, such that the operator \({\mathbf {R}}^{(n)}\) is expressed as a sum  and
and
-
(1)
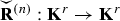 is a trace class operator, while
is a trace class operator, while -
(2)
\(\widehat{\mathbf {R}}^{(n)}:\mathbf {K}^{r}\rightarrow \mathbf {K}^{r}\) is upper triangular and satisfies
$$\begin{aligned} \Vert \widehat{\mathbf {R}}^{(n)}\Vert \leqslant C (r''_0)^{-n}. \end{aligned}$$
Proof
Using the periodic partition of unity \(\{q_\omega \}_{\omega \in \mathbb {Z}}\) defined in (6.1), we setFootnote 31
so that \( \sum _{\omega \geqslant [2t_0]-1} q_{\omega }^{(n)}(t)= (1-\chi (t/(2t_0))\cdot (t^{n-1}e^{-s_0 t})/(n-1)!\) and that
from the definition (B.5). We deduce the claims of the lemma from \(\square \)
Claim 1
For arbitrarily small \(\tau >0\), there exists a constant \(C>0\), independent of n, such that the operators \(\mathbf {L}(q_{\omega }^{(n)})\) for \(n\geqslant 1\) are decomposed as

where \(\widehat{\mathbf {L}}(q_{\omega }^{(n)})\) are upper triangular and satisfy
while  are trace class operators satisfying
are trace class operators satisfying

From the claim above, we set

Then the first claim (1) of the lemma follows from (B.11). The second claim (2) also follows because \(\widehat{\mathbf {R}}^{(n)}\) is upper triangular from Lemma B.4 and because
from (B.10). We give the proof of Claim 1 below to complete the proof.
Proof of Claim 1
We first note that the family
satisfies the assumption in Lemma B.5. To proceed, we write an integer \(\omega \geqslant [2t_0]-1\) as a sum of real numbers in \([t_0,2t_0]\):
Then we decompose \({\mathbf {L}}(q_{\omega }^{(n)})\) as follows: First we write
where we set \(\tilde{q}_{\omega }^{(n)}(t)=q_{\omega }^{(n)}(t+\omega )\) for brevity. Since the first term on the right-hand side other than the first factor is of the same form as \({\mathbf {L}}(\tilde{q}_{\omega }^{(n)})\circ \mathbf {L}^{\omega }\), we apply the parallel operation to it. If we continue this procedure, we can express \(\mathbf {L}(q_{\omega }^{(n)})\) as
Note that, from Lemma B.5 and the estimate noted in the beginning, we see

where \(\widehat{\mathbf {L}}\) is upper triangular and \(\Vert \widehat{\mathbf {L}}\Vert \leqslant C\) while  is in the trace class and
is in the trace class and  , with \(C>0\) a constant independent of n and \(\omega \). So we may rewrite the first term on the right-hand side of (B.13) as
, with \(C>0\) a constant independent of n and \(\omega \). So we may rewrite the first term on the right-hand side of (B.13) as

Let \(\widehat{\mathbf {L}}(q_{\omega }^{(n)})\) in Claim 1 be the first term of (B.14) above and  be the remainder, that is, the sum of the second term in (B.14) and the sum on the second line of (B.13). By Lemma B.4, \(\widehat{\mathbf {L}}(q_{\omega }^{(n)})\) is upper triangular. Since
be the remainder, that is, the sum of the second term in (B.14) and the sum on the second line of (B.13). By Lemma B.4, \(\widehat{\mathbf {L}}(q_{\omega }^{(n)})\) is upper triangular. Since
from Remark 11.16, we obtain the estimate (B.10) immediately. Also, for the second term in (B.14), we have

and this bound is summable with respect to \(\omega \). To look into the sum in (B.13), note that the operator \(({\mathbf {L}}^{t_{j}}-\mathbf {L}^{t_{j}}_{\mathrm {hyp},\hookrightarrow })\circ {\mathbf {L}}(\tilde{q}_{\omega }^{(n)})\) satisfies
for a constant \(C>0\) independent of n and \(\omega \), from the latter claim of Lemma B.5 and uniform boundedness of \(\mathcal {P}\). Hence we have
This bound is again summable with respect to \(\omega \), provided \(\tau \) is sufficiently small. Therefore we obtain the estimate (B.11). \(\square \)
Corollary B.9
The essential spectral radius of \(\mathcal {R}(s_0):\widetilde{\mathcal {K}}^{r}(K_0)\rightarrow \widetilde{\mathcal {K}}^{r}(K_0)\) is bounded by \((r''_0)^{-1}\).
Proof
We consider the decomposition of \(\mathcal {R}(s_0)^n:{\widetilde{\mathcal {K}}}^{r}(K_0)\rightarrow {\widetilde{\mathcal {K}}}^{r}(K_0)\) into

where \(\widetilde{\mathcal {R}}^{(n)}\) is that in (B.9). From the last lemma, the operator norm of \(\widehat{\mathcal {R}}^{(n)}\) on \(\mathcal {K}^r(K_0)\) is bounded by \(C (r''_0)^{-n}\) with \(C>0\) independent of n, and  on \(\mathcal {K}^r(K_0)\) is a trace class operator. Further it is not difficult to see that these remain true when we regard \(\widehat{\mathcal {R}}^{(n)}\) and
on \(\mathcal {K}^r(K_0)\) is a trace class operator. Further it is not difficult to see that these remain true when we regard \(\widehat{\mathcal {R}}^{(n)}\) and  as operators on \({\widetilde{\mathcal {K}}}^{r}(K_0)\), because \(\mathcal {L}^{t_0}:{\widetilde{\mathcal {K}}}^{r}(K_0)\rightarrow \mathcal {K}^r(K_0)\) is bounded from Proposition 7.8. Therefore, recalling Remark B.7 for \(\widetilde{\mathcal {R}}^{(n)}\), we obtain that the essential spectral radius of \(\mathcal {R}(s_0)^n\) is bounded by \(C (r''_0)^{-n}\) and hence by \((r''_0)^{-n}\) from the multiplicative property of essential spectral radius. \(\square \)
as operators on \({\widetilde{\mathcal {K}}}^{r}(K_0)\), because \(\mathcal {L}^{t_0}:{\widetilde{\mathcal {K}}}^{r}(K_0)\rightarrow \mathcal {K}^r(K_0)\) is bounded from Proposition 7.8. Therefore, recalling Remark B.7 for \(\widetilde{\mathcal {R}}^{(n)}\), we obtain that the essential spectral radius of \(\mathcal {R}(s_0)^n\) is bounded by \(C (r''_0)^{-n}\) and hence by \((r''_0)^{-n}\) from the multiplicative property of essential spectral radius. \(\square \)
Corollary B.9 implies that the spectral set of \(\mathcal {R}(s_0):{\widetilde{\mathcal {K}}}^{r}(K_0)\rightarrow {\widetilde{\mathcal {K}}}^{r}(K_0)\) on the outside of the disk \(|z|\leqslant (r'_0)^{-1}\) consists of discrete eigenvalues \(\mu _i\), \(1\leqslant i\leqslant m\), counted with multiplicity. Since \(A \mathcal {R}(s_0)=s_0 \mathcal {R}(s_0)+1\), we have
This implies that \(\mu _i\)’s are in one-to-one correspondence to the eigenvalues \(\chi _i\), \(1\leqslant i\leqslant m\), of the generator A in the disk \(D(s_0,r'_0)\) by the relation
Remark B.10
Since the argument above holds for any \(s_0\) satisfying \(\mathrm {Re}(s_0)>P\), the spectrum of the generator A on the half-plane \(\mathrm {Re}(s)>-(1/4)r\chi _0\) consists of discrete eigenvalues with finite multiplicity and the resolvent \(\mathcal {R}(s)\) is meromorphic on that half-plane.
Let \(\varvec{\pi }:\widetilde{\mathcal {K}}^{r}(K_0)\rightarrow \widetilde{\mathcal {K}}^{r}(K_0)\) be the spectral projector of \(\mathcal {R}(s_0)\) for the spectral set \(\{\mu _i\}_{i=1}^m\) on the outside of the disk \(|z|\leqslant r_0^{-1}\). This is also the spectral projector of the generator A for the spectral set \(\{\chi _i\}_{i=1}^m\) and its image is contained in \(\mathcal {K}^{r}(K_0)\) from Proposition 7.8. We set \( \mathcal {F}(s_0)=\varvec{\pi }\circ \mathcal {R}(s_0)\), so that
Our task is to prove (B.3) in Proposition B.1 for
To continue, let \(N_0>0\) be a large integer constant which will be specified later in the course of the argument. Consider large integer n and write
where \(n=n(1)+n(2)+\cdots +n(I)\) with \(N_0\leqslant n(i)\leqslant 2N_0\). We decompose each term \(\mathcal {R}(s_0)^{n(i)}\) on the right-hand side as
in the same manner as (B.9). From Remark B.7, the part \(\widetilde{\mathcal {R}}^{(n(i))}\) is very small in the operator norm if we let the constant \(N_0\) be sufficiently large. (And note that the following argument is much simpler if we ignore this part.)
Since the operators \(\mathcal {R}^{(n(i))}\) and \(\widetilde{\mathcal {R}}^{(n(i))}\) for \(1\leqslant i\leqslant I\) commute each other and also with the projection operator \(\varvec{\pi }\), we can express \(\mathcal {R}(s_0)^n-\mathcal {F}(s_0)^n\) as the sum of the \(2^I\) terms of the form
where \(\{n''(1),\ldots , n''(I''), n'(1), \ldots , n'(I')\}\) with \(I=I'+I''\) ranges over all the rearrangements of \(\{n(1), n(2), \ldots , n(I)\}\). Hence our task is reduced to show
Claim 2
There exists a constant \(C>0\) such that
Proof of Claim 2
Below we prove the claim in the case \(I'\geqslant I''\) because, otherwise, we can get the conclusion by a similar but much easier argument using Remark B.9. We translate the claim to that on the lifted operators. Let us put
We write
so that
Then, from Corollary B.6, the inequality in Claim 2 is equivalent to
Since we are assuming \(I'\geqslant I''\) and since the operators on the left hand side above commute, we may write the operator on the left-hand side above as
From the choice of the spectral projector \(\varvec{\pi }\) and the fact that \(\widetilde{\mathbf {R}}^{(n)}\) has small operator norm by the same reason as noted in Remark B.7, we get the estimate
provided that the constant \(N_0\) is sufficiently large, where we set
By Lemma B.8, the operators \(\mathbf {R}_i\) are decomposed as  where
where
-
(1)
 is a trace class operator and
is a trace class operator and  , and
, and -
(2)
\(\widehat{\mathbf {R}}_i\) is upper triangular and satisfies \( \Vert \widehat{\mathbf {R}}_i\Vert \leqslant r_0^{-\tilde{n}(i)}/4\)
provided that the constant \(N_0\) is sufficiently large. (For the case \(1\leqslant i\leqslant I''\), we need a slight modification of Lemma B.8 but the proof goes as well.) In (B.20), we consider the decomposition

and apply the development it in the parallel manner as we used to obtain (B.13). Then, noting that \(\mathrm {Tr}^\flat \, (\widehat{\mathbf {R}}_1\circ \cdots \circ \widehat{\mathbf {R}}_{I'})=0\) from Lemma B.4, we obtain

This is bounded in absolute value by

The trace norm  is bounded by a constant C independent of j and n. Therefore, using the condition on \(\widehat{\mathbf {R}}_i\) and (B.21), we conclude (B.19). This completes the proof of Claim 2 and hence that of Proposition B.1. \(\square \)
is bounded by a constant C independent of j and n. Therefore, using the condition on \(\widehat{\mathbf {R}}_i\) and (B.21), we conclude (B.19). This completes the proof of Claim 2 and hence that of Proposition B.1. \(\square \)
Rights and permissions
About this article
Cite this article
Faure, F., Tsujii, M. The semiclassical zeta function for geodesic flows on negatively curved manifolds. Invent. math. 208, 851–998 (2017). https://doi.org/10.1007/s00222-016-0701-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00222-016-0701-5



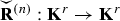 is a trace class operator, while
is a trace class operator, while is a trace class operator and
is a trace class operator and  , and
, and