An analytical solution for one-dimensional contaminant diffusion through multi-layered system and its applications

Abstract

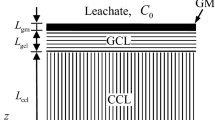
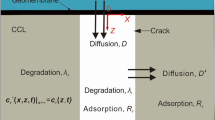
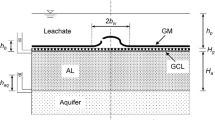
An analytical solution for one-dimensional contaminant diffusion through multi-layered media is derived regarding the change of the concentration of contaminants at the top boundary with time. The model accounts for the arbitrary initial conditions and the conditions of zero concentration and zero mass flux on the bottom boundary. The average degree of diffusion of the layered system is introduced on the basis of the solution. The results obtained by the presented analytical solutions agree well with those obtained by the numerical methods presented in the literature papers. The application of the analytical solution to the problem of landfill liner design is illustrated by considering a composite liner consisting of geomembrane and compacted clay liner. The results show that the 100-year mass flux of benzene at the bottom of the composite liner is 45 times higher than that of acetone for the same composite liner. The half-life of the contaminant has a great influence on the solute flux of benzene diffused into the underlying aquifer. Results also indicates that an additional 2.9–5.0 m of the conventional (untreated) compacted clay liner under the geomembrane is required to achieve the same level of protection as provided by 0.60 m of the Hexadecyltrimethylammonium (HDTMA)-treated compacted clay liners in conjunction with the geomembrane. Applications of the solution are also presented in the context of a contaminated two-layered media to demonstrate that different boundary and initial conditions can greatly affect the decontamination rate of the problem. The method is relatively simple to apply and can be used for performing equivalency analysis of landfill liners, preliminary design of groundwater remediation system, evaluating experimental results, and verifying more complex numerical models.

Appendix: Solutions

A1 solution for ϕ _i (z)

The governing equation for the sub-problem for ϕ _i (z) is as follows:

$$ \frac{{{\text{d}}^{2} \phi_{i} \left( z \right)}}{{{\text{d}}z^{2} }} = 0. $$

(25)

The boundary conditions for this problem are as follows:

$$ \phi_{1} \left( 0 \right) = 1 $$

(26)

$$ \phi_{i} \left( {z_{i} } \right) = \phi_{i + 1} \left( {z_{i} } \right),\quad i = 1,2,3, \ldots ,n $$

(27)

$$ n_{i} D_{i}^{*} \frac{{{\text{d}}\phi_{i} \left( {z_{i} } \right)}}{{{\text{d}}z}} = n_{i + 1} D_{i + 1}^{*} \frac{{{\text{d}}\phi_{i + 1} \left( {z_{i} } \right)}}{{{\text{d}}z}},\quad i = 1,2,3, \ldots ,n $$

(28)

$$ \phi_{n} \left( z \right)\left| {_{z = H} } \right. = 0\quad ({\text{for the Dirichlet boundary}}) $$

(29)

$$ \frac{{{\text{d}}\phi_{n} \left( z \right)}}{{{\text{d}}z}}\left| {_{z = H} } \right. = 0\quad ({\text{for the Neumann boundary}}). $$

(30)

Obviously, the solution to Eq. 25 satisfying all relevant boundary conditions is:

$$ \phi_{i} \left( z \right) = P_{i} + Q_{i} z $$

(31)

where P _i and Q _i can be obtained using the boundary conditions (Eqs. 26–30).

A2 Solution for θ _i (z,t)

The governing equation for sub-problem θ _i (z, t) can be written as follows:

$$ \frac{{\partial \theta_{i} \left( {z,t} \right)}}{\partial t} = \frac{{D_{i}^{*} }}{{R_{di} }}\frac{{\partial^{2} \theta_{i} \left( {z,t} \right)}}{{\partial z^{2} }}\quad \left( {i = 1,2,3, \ldots ,n} \right) $$

(32)

The boundary conditions for this problem are:

$$ \theta_{1} \left( {0,t} \right) = 0 $$

(33)

$$ \theta_{i} \left( {z_{i} ,t} \right) = \theta_{i + 1} \left( {z_{i} ,t} \right),\quad \;i = 1,2,3, \ldots ,n $$

(34)

$$ n_{i} D_{i}^{*} \frac{{\partial \theta_{i} \left( {z_{i} ,t} \right)}}{\partial z} = n_{i + 1} D_{i + 1}^{*} \frac{{\partial \theta_{i + 1} \left( {z_{i} ,t} \right)}}{\partial z},\;\quad i = 1,2,3, \ldots ,n $$

(35)

$$ \theta_{n} \left( {H,t} \right) = 0\quad ({\text{for the Dirichlet boundary}}) $$

(36)

$$ \frac{{\partial \theta_{n} \left( {H,t} \right)}}{\partial z} = 0\quad ({\text{for the Neumann boundary}}) $$

(37)

The initial condition is:

$$ \theta_{i} \left( {z,0} \right) = f_{i} (z) - \phi_{i} \left( z \right)C_{u} (0). $$

(38)

The chemical process of diffusion and the process of small-strain consolidation are mathematically analogous because they are both governed by the same form of a second-order partial differential equation (Shackelford and Lee 2005). According to this analogy, using the method described by Lee et al. (1992) for consolidation of layered soil, the solution to Eq. 32 satisfying all relevant conditions can be expressed as follows:

$$ \theta_{i} \left( {z,t} \right) = \sum\limits_{m = 1}^{\infty } {\varsigma_{m} } g_{mi} \left( z \right){\text{e}}^{{ - \beta_{m} t}} $$

(39)

where

$$ \beta_{m} = \frac{{\lambda_{m}^{2} D_{1}^{*} }}{{R_{d1} h_{1}^{2} }} $$

(40)

$$ g_{mi} \left( {z,t} \right) = A_{mi} \sin \left( {\mu_{i} \lambda_{m} \frac{z}{{h_{1} }}} \right) + B_{mi} \cos \left( {\mu {}_{i}\lambda_{m} \frac{z}{{h_{1} }}} \right),\quad i = 1,2,3, \ldots ,n $$

(41)

$$ \mu_{i} = \sqrt {\frac{{D_{1}^{*} R_{di} }}{{D_{i}^{*} R_{d1} }}} $$

(42)

$$ \varsigma_{m} = \frac{{\sum\nolimits_{i = 1}^{n} {\frac{{n_{i} R_{di} }}{{n_{1} R_{d1} }}\int_{{z_{i - 1} }}^{{z_{i} }} {g_{mi} \left( z \right)\left[ {f_{i} \left( z \right) - \phi_{i} \left( z \right)C_{u} \left( 0 \right)} \right]{\text{d}}z} } }}{{\sum\nolimits_{i = 1}^{n} {\frac{{n_{i} R_{di} }}{{n_{1} R_{d1} }}\int_{{z_{i - 1} }}^{{z_{i} }} {g^{2}_{mi} \left( z \right){\text{d}}z} } }}. $$

(43)

The coefficients A _mi and B _mi in Eq. 41 can be determined by the following recurrence equation:

$$ \left. {\begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} {A_{m1} } & {B_{m1} } \\ \end{array} } \right]^{\text{T}} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ \end{array} } \right]^{\text{T}} } \\ {\left[ {\begin{array}{*{20}c} {A_{mi} } & {B_{mi} } \\ \end{array} } \right]^{\text{T}} = S_{i} \left[ {\begin{array}{*{20}c} {A_{m(i - 1)} } & {B_{m(i - 1)} } \\ \end{array} } \right]^{\text{T}} \quad i = 2,3, \ldots ,n} \\ \end{array} } \right\} $$

(44)

in which:

$$ S_{i} = \left[ {\begin{array}{*{20}c} {A_{i} B_{i} + \eta_{i} E_{i} F_{i} } & {A_{i} F_{i} - \eta_{i} E_{i} B_{i} } \\ {E_{i} B_{i} - \eta_{i} A_{i} F_{i} } & {E_{i} F_{i} + \eta_{i} A_{i} B_{i} } \\ \end{array} } \right], $$

$$ A_{i} = \sin \left( {\mu_{i} \lambda_{m} \frac{{z_{i - 1} }}{{h_{1} }}} \right),\quad B_{i} = \sin \left( {\mu_{i - 1} \lambda_{m} \frac{{z_{i - 1} }}{{h_{1} }}} \right), $$

$$ E_{i} = \cos \left( {\mu_{i} \lambda_{m} \frac{{z_{i - 1} }}{{h_{1} }}} \right),\quad F_{i} = \cos \left( {\mu_{i - 1} \lambda_{m} \frac{{z_{i - 1} }}{{h_{1} }}} \right), $$

$$ \eta_{i} = \frac{{n_{i - 1} }}{{n_{i} }}\sqrt {\frac{{D_{i - 1}^{*} R_{{d\left( {i - 1} \right)}} }}{{D_{i}^{*} R_{di} }}} . $$

The eigenvalues λ _m are obtained by finding the roots of the following characteristic equation:

$$ S_{n + 1} \cdot S_{n} \cdot S_{n - 1} \cdot \cdot \cdot S_{2} \cdot S_{1} = 0, $$

(45)

in which

$$ S_{1} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ \end{array} } \right]^{\text{T}} $$

(46)

$$ S_{n + 1} = \left[ {\begin{array}{*{20}c} {B_{n + 1} } & {F_{n + 1} } \\ \end{array} } \right]\quad ({\text{for the Dirichlet boundary}}) $$

(47)

$$ S_{n + 1} = \left[ {\begin{array}{*{20}c} {F_{n + 1} } & { - B_{n + 1} } \\ \end{array} } \right]\quad ({\text{for the Neumann boundary}}). $$

(48)

Because the eigenvalues and the coefficients A _mi and B _mi are calculated directly from Eqs. 45 and 40, respectively, the computation is dramatically simplified and proved to be very efficient (Lee et al. 1992).