Average abundancy of cooperation in multi-player games with random payoffs

Abstract

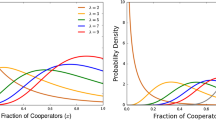
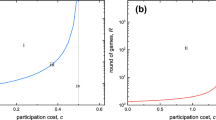
We consider interactions between players in groups of size $d\ge 2$ with payoffs that not only depend on the strategies used in the group but also fluctuate at random over time. An individual can adopt either cooperation or defection as strategy and the population is updated from one time step to the next by a birth-death event according to a Moran model. Assuming recurrent symmetric mutation and payoffs to cooperators and defectors according to the composition of the group whose expected values, variances, and covariances are of the same small order, we derive a first-order approximation for the average abundance of cooperation in the selection-mutation equilibrium. In general, we show that increasing the variance of any payoff for defection or decreasing the variance of any payoff for cooperation increases the average abundance of cooperation. As for the effect of the covariance between any payoff for cooperation and any payoff for defection, we show that it depends on the number of cooperators in the group associated with these payoffs. We study in particular the public goods game, the stag hunt game, and the snowdrift game, all social dilemmas based on random benefit b and random cost c for cooperation, which lead to correlated payoffs to cooperators and defectors within groups. We show that a decrease in the scaled variance of b or c, or an increase in their scaled covariance, makes it easier for weak selection to favor the abundance of cooperation in the stag hunt game and the snowdrift game. The same conclusion holds for the public goods game except that the variance of b has no effect on the average abundance of C. Moreover, while the mutation rate has little effect on which strategy is more abundant at equilibrium, the group size may change it at least in the stag hunt game with a larger group size making it more difficult for cooperation to be more abundant than defection under weak selection.

Appendices

Appendix A: Conditional expected frequency change

For $i/N=x$, we have

$$\begin{aligned} \frac{\left( {\begin{array}{c}i-1\\ k\end{array}}\right) \left( {\begin{array}{c}N-i\\ n-k\end{array}}\right) }{\left( {\begin{array}{c}N-1\\ n\end{array}}\right) }&=\left( {\begin{array}{c}n\\ k\end{array}}\right) \frac{(i-1)\times \cdots \times (i-k)\times (N-i)\times \cdots \times (N-i-n+k+1)}{(N-1)\times \cdots \times (N-n)}\nonumber \\&=\left( {\begin{array}{c}n\\ k\end{array}}\right) \frac{(x-\frac{1}{N})\times \cdots \times (x-\frac{k}{N})\times (1-x)\times \cdots \times (1-x-\frac{n-k-1}{N})}{(1-\frac{1}{N})\times \cdots \times (1-\frac{n}{N})}\nonumber \\&=\left( {\begin{array}{c}n\\ k\end{array}}\right) x^{k}(1-x)^{n-k}+O(N^{-1}). \end{aligned}$$

(75)

Therefore, in the limit of a large population size N, the average payoffs to C and D in (3) can be written as

$$\begin{aligned} P_C(x)&=\sum _{k=0}^{d-1}\left( {\begin{array}{c}d-1\\ k\end{array}}\right) x^k(1-x)^{d-k-1}a_k, \end{aligned}$$

(76a)

$$\begin{aligned} P_D(x)&=\sum _{k=0}^{d-1}\left( {\begin{array}{c}d-1\\ k\end{array}}\right) x^k(1-x)^{d-k-1}b_k. \end{aligned}$$

(76b)

Using (1), the first two moments of the average payoff to C in (3) when the frequency of C is x are given by

$$\begin{aligned} E\Big [P_C(x)\Big ]&=\delta \sum _{k=0}^{d-1}\left( {\begin{array}{c}d-1\\ k\end{array}}\right) x^k(1-x)^{d-k-1}\mu _{C,k}+o(\delta ), \end{aligned}$$

(77a)

$$\begin{aligned} E\Big [P_C^2(x)\Big ]&=\delta \sum _{k,l=0}^{d-1}\left( {\begin{array}{c}d-1\\ k\end{array}}\right) \left( {\begin{array}{c}d-1\\ l\end{array}}\right) x^{k+l}(1-x)^{2d-k-l-2}\sigma _{CC,kl}+o(\delta ), \end{aligned}$$

(77b)

and similarly the first two moments of $P_D(x)$ by

$$\begin{aligned} E\Big [P_D(x)\Big ]&=\delta \sum _{k=0}^{d-1}\left( {\begin{array}{c}d-1\\ k\end{array}}\right) x^k(1-x)^{d-k-1}\mu _{D,k}+o(\delta ), \end{aligned}$$

(78a)

$$\begin{aligned} E\Big [P_D^2(x)\Big ]&=\delta \sum _{k,l=0}^{d-1}\left( {\begin{array}{c}d-1\\ k\end{array}}\right) \left( {\begin{array}{c}d-1\\ l\end{array}}\right) x^{k+l}(1-x)^{2d-k-l-2}\sigma _{DD,kl}+o(\delta ). \end{aligned}$$

(78b)

Moreover, we have

$$\begin{aligned} E\Big [P_C(x)P_D(x)\Big ]\!=\!\delta \sum _{k,l=0}^{d-1}\left( {\begin{array}{c}d-1\\ k\end{array}}\right) \left( {\begin{array}{c}d-1\\ l\end{array}}\right) x^{k+l}(1\!-\!x)^{2d-k-l-2}\sigma _{CD,kl}\!+\!o(\delta ).\qquad \end{aligned}$$

(79)

We are interested in

$$\begin{aligned} E\left[ \frac{f_C(x)-f_D(x)}{xf_C(x)+(1-x)f_D(x)}\right] =E\left[ \frac{P_C(x)-P_D(x)}{1+{\bar{P}}(x)}\right] , \end{aligned}$$

(80)

where ${\bar{P}}(x)=xP_C(x)+(1-x)P_D(x)$ is the average payoff in the population. We expand the last expression by the delta-method (Lynch and Walsh 1998; Rice and Papadopoulos 2009), which gives

(81)

for two random variables Y and Z with

(82)

and

(83)

for $k \ge 1$. For $Y=P_C(x)-P_D(x)$ and $Z=1+{\bar{P}}(x)$, using the facts that

(84)

for $k\ge 2$ and

(85)

for $k\ge 1$, we obtain

(86)

Note that

(87)

and $\left( 1+E[{\bar{P}}(x)]\right) ^{2}=1+O(\delta )$, so that

$$\begin{aligned} E\left[ \frac{P_C(x)-P_D(x)}{1+{\bar{P}}(x)}\right]&=E[P_C(x)]-E[P_D(x)] -E\left[ \left( P_C(x)-P_D(x)\right) {\bar{P}}(x)\right] +o(\delta )\nonumber \\&=E[P_C(x)]-E[P_D(x)]-xE[P^2_1(x)]+(2x-1)E[P_C(x)P_D(x)]\nonumber \\&\quad +(1-x)E[P^2_2(x)]+o(\delta )\nonumber \\&=m(x)\delta +o(\delta ), \end{aligned}$$

(88)

where

$$\begin{aligned} m(x)&=\sum _{k=0}^{d-1}\left( {\begin{array}{c}d-1\\ k\end{array}}\right) x^k(1-x)^{d-k-1}\left( \mu _{C,k}-\mu _{D,k}\right) +\sum _{k,l=0}^{d-1}\left( {\begin{array}{c}d-1\\ k\end{array}}\right) \left( {\begin{array}{c}d-1\\ l\end{array}}\right) \nonumber \\&\quad \times x^{k+l}(1-x)^{2d-k-l-2}\Big [-x\sigma _{CC,kl}+(1-x)\sigma _{DD,kl}+((x-(1-x))\sigma _{CD,kl}\Big ]. \end{aligned}$$

(89)

Appendix B: Moments of the Dirichlet distribution

The ancestry of a random sample of n individuals is described backward in time by a coalescent tree with every pair of lines at any given time back coalescing at rate 1 independently of all the others (Kingman 1982). Moreover, mutations occur independently on each lines of the coalescent tree according to a Poisson process of intensity $\theta >0$. When there is mutation, the mutant type is 1 or 2 with probability 1/2 for each type independently of the parental type. A line is said to be ancestral to the sample as long as no mutation has occurred on it. We are interested in the probability distribution of the sample configuration, more precisely the probability for k labeled individuals to be of type 1 and the $n-k$ others to be of type 2, denoted by $\psi _n^k$, for $0\le k\le n$.

In order to determine the sample probability distribution, we will extend an approach used in Griffiths and Lessard (2005) to show the Ewens sampling formula (Ewens 1972) in the case where the mutant type is always a novel type. See also Hoppe (1984) and Joyce and Tavaré (1987) for related approaches based on urn models and cycles in permutations.

Note first that the number of ancestral lines of a sample of n individuals is a death process backward in time, where ancestral lines are lost by either mutation or coalescence. This death process was studied in Griffiths (1980) and Tavaré (1984), and the events in this death process called defining events in Ewens (1990).

Label the n sampled individuals and list them in the order in which their ancestral lines are lost backward in time, following either a mutation or a coalescence. In the case of coalescence, one of the two lines involved is chosen at random to be the one that is lost, the other one being the continuing line. There are n! different orders.

Let us first consider the probability for the n sampled individuals in a given order to be all of type 1. Note that this event occurs if and only if all ancestral lines lost by mutation lead to type 1. Now let us look at the probability of each defining event. When i ancestral lines remain, the total rate of mutation is $i\theta$ and the total rate of coalescence is $i(i-1)/2$, while the rate of mutation leading to type 1 on any particular ancestral line is $\theta /2$ and the rate of coalescence involving any particular ancestral line and leading to its loss is $(i-1)/2$. Therefore, the probability that a particular ancestral line is the next one lost and that it is lost by mutation leading to type 1 is $(\theta /2)/[(i\theta +i(i-1)/2]$ for $i\ge 1$. Similarly, the probability that a particular ancestral line is the next one lost and that it is lost by coalescence is $[(i-1)/2]/[(i\theta +i(i-1)/2]$ for $i\ge 1$. Summing these probabilities, multiplying the sums for $i=n, n-1, \ldots , 1$, and considering all possible orders, we get

$$\begin{aligned} \psi _n^0&=n! \, \prod _{i=1}^{n} \left( \frac{\theta /2 + (i-1)/2}{i\theta +i(i-1)/2} \right) = \frac{\prod _{i=1}^{n}(\theta + i-1)}{ \prod _{i=1}^{n}(2\theta +i-1)} \end{aligned}$$

(90)

as probability for the n sampled individuals to be of type 1.

Now let us look at the general case of k labeled individuals of type 1 and $n-k$ of type 2. When i ancestral lines of individuals of type 1 and j ancestral lines of individuals of type 2 remain, the total rate of mutation is $(i+j)\theta$ and the total rate of coalescence is $(i+j)(i+j-1)/2$, while any particular ancestral line of an individual is lost by mutation to the type of the individual, whose rate is $\theta /2$, or by coalescence with ancestral lines of individuals of the same type, whose rate is $(i-1)/2$ for type 1 and $(j-1)/2$ for type 2. Considering i and j decreasing from k and $n-k$ to 0 or 1 with $i+j=n, n-1, \ldots , 1$, we get

$$\begin{aligned} \psi _n^k&=n! \, \frac{\prod _{i=1}^{k}(\theta /2 + (i-1)/2) \prod _{j=1}^{n-k}(\theta /2 + (j-1)/2)}{ \prod _{l=1}^{n}(l\theta +l(l-1)/2)} \nonumber \\&=\frac{\prod _{i=1}^{k}(\theta +i-1)\prod _{j=1}^{n-k}(\theta +j-1)}{\prod _{l=1}^{n}(2\theta +l-1)}\nonumber \\&=\frac{\Gamma (2\theta )}{ \Gamma (2\theta +n) } \left( \frac{\Gamma (\theta +k)\Gamma (\theta +n-k)}{ \Gamma (\theta )^2}\right) \end{aligned}$$

(91)

as probability for k labeled individuals to be of type 1 and the $n-k$ others to be of type 2 in a random sample of size n. Here, we use $\Gamma (\beta +1 )= \beta \Gamma (\beta )$ for $\beta >0$. Note that $\psi _n^k=\psi _{n-k}^k$.

Applying the same approach as above for K types with rate of mutation to type k given by $\alpha _k/2 >0$ for $k=1, \ldots , K$ with $\alpha _1 + \cdots + \alpha _K=\alpha$, the probability for $n_k$ labeled individuals to be of type k for $k=1, \ldots , K$ in a random sample of size $n=n_1 + \cdots + n_K$ is given by

$$\begin{aligned} \psi _n^{n_1, \ldots , n_K}&= \frac{\prod _{k=1}^{K}\prod _{i_k=1}^{n_k}(\alpha _k + i_k-1)}{ \prod _{i=1}^{n}(\alpha +i -1)} \nonumber \\&=\frac{\Gamma (\alpha )}{\Gamma (\alpha + n)}\prod _{k=1}^{K} \frac{\Gamma (\alpha _k + n_k)}{ \Gamma (\alpha _k)}. \end{aligned}$$

(92)

These are the moments of the Dirichlet distribution (see, e.g., Balakrishnan and Nevzorov 2003).