Computing (Un)stable Manifolds with Validated Error Bounds: Non-resonant and Resonant Spectra

Abstract

We develop techniques for computing the (un)stable manifold at a hyperbolic equilibrium of an analytic vector field. Our approach is based on the so-called parametrization method for invariant manifolds. A feature of this approach is that it leads to a posteriori analysis of truncation errors which, when combined with careful management of round off errors, yields a mathematically rigorous enclosure of the manifold. The main novelty of the present work is that, by conjugating the dynamics on the manifold to a polynomial rather than a linear vector field, the computer-assisted analysis is successful even in the case when the eigenvalues fail to satisfy non-resonance conditions. This generically occurs in parametrized families of vector fields. As an example, we use the method as a crucial ingredient in a computational existence proof of a connecting orbit in an amplitude equation related to a pattern formation model that features eigenvalue resonances.

1 Introduction

Stable and unstable manifolds are fundamental building blocks for understanding the global dynamics of nonlinear differential equations. Since closed-form analytic expressions for stable/unstable manifolds are rarely available, considerable effort goes into developing numerical techniques for their approximation, see e.g., Krauskopf et al. (2005), Haro and da la Llave (2006), Beyn and Kless (1998) and Castelli et al. (2015) and the references therein. One powerful tool for studying invariant manifolds (stable, unstable, strongly (un)stable and even more general ones) is the parameterization method of Cabré et al. (2003a, b, 2005). The parameterization method is based on formulating certain operator equations (invariance equations) which simultaneously describe both the dynamics on the manifold and its embedding. The method has been implemented numerically to study a variety of problems involving stable and unstable manifolds of equilibria and fixed points (Mireles-James 2013; Mireles-James and Mischaikow 2013; Mireles James and Lomelí 2010; Haro 2011; van den Berg et al. 2011), stable/unstable manifolds of periodic orbits for differential equations (Guillamon and Huguet 2009; Huguet and de la Llave 2013; Castelli et al. 2015), quasi-periodic invariant sets in dynamical systems (Haro and da la Llave 2006) and more recently in order to simultaneously compute invariant manifolds with their unknown dynamics (Canadell and Haro 2014; Haro et al. 2014), to mention just a few examples.

The last reference is a book which provides many other examples and much fuller discussion of the literature.

In addition to facilitating efficient numerical computations, the functional analytic framework of the parameterization method also provides a natural setting for a posteriori analysis of errors. The works of van den Berg et al. (2011), Mireles-James and Mischaikow (2013) and Mireles-James (2015) exploit this a posteriori analysis and implement mathematically rigorous numerical validation methods for the stable and unstable manifolds. The term “validation” here expresses the fact that the computations provide explicit bounds on all approximation errors involved.

Approximate parametrizations are often computed by substituting a power series ansatz into the invariance equation and deriving a sequence of homological equations for the power series coefficients. These homological equations are then solved recursively to any desired order. In this paper we employ an alternative methodology for solving the invariance equation. We recast the infinite system of homological equations as a nonlinear zero finding problem on a Banach space of geometrically decaying sequences, and we implement a parametrized Newton–Kantorovich argument in the style of Yamamoto (1998).

There are three advantages to using a Newton method. First, we note the works of van den Berg et al. (2011), Mireles-James and Mischaikow (2013) and Mireles-James (2015) assume that certain non-resonance conditions between the eigenvalues are satisfied. The main goal of the present work is to weaken this assumption. We build on the theory of Cabré et al. (2003a, b, 2005) and develop computer-assisted methods for rigorous error bounding even in the face of a resonance. More precisely we develop validation schemes which apply at any co-dimension one resonance between the eigenvalues. The formulation of the resonant as well as non-resonant zero finding problems on an infinite sequence space unifies the presentation and implementation as well as the necessary a posteriori analysis.

Second, the zero finding methodology based on a numerical Newton method for the truncated problem leads to improved numerical performance even in the case where validated numerics are not desired. The Newton iteration can always be started from the linear approximation of the manifold by its eigenvectors; however, one has the option of improving the convergence by starting the iteration from a polynomial obtained by solving a few of the lower-order homological equations recursively. Once the iteration begins the order of the polynomial approximation is roughly doubled at each step. The freedom one has in choosing the lengths of the eigenvectors is exploited in order to guarantee that the Taylor coefficients decay at the desired rate. A similar numerical Newton scheme for computing invariant manifolds in discrete time dynamical systems (without rigorous validation) was used in Mireles James and Lomelí (2010). Indeed this kind of Newton scheme is always needed when the parameterization method is applied in Fourier space, see again Haro et al. (2014) and the references therein.

Third, existing rigorous continuation methods (van den Berg et al. 2010; Breden et al. 2013) are directly applicable to our novel approach, thus putting the rigorous computation of branches of connecting orbits within direct reach. Of course, from the viewpoint of continuation, all three advantages are crucial. Indeed, while continuing along one-parameter families of (un)stable manifolds resonances are encountered generically and are thus unavoidable.

Our use of parameterized Newton–Kantorovich arguments is guided by the work of a number of authors on the so-called method of radii polynomials. This method provides a tool kit for solution and continuation of zero finding problems in infinite dimensions. In this method one derives certain polynomials whose coefficients encode information about the approximate solution, the choice of approximate inverse of the derivative, the local regularity properties of the problem and the choice of Banach space on which to work. Once these givens are fixed the roots of the radii polynomials yield not only existence and uniqueness results, but also tight error estimates and isolation bounds for the problem. Radii polynomial methods have been applied successfully to a number of problems in dynamical systems, partial differential equations and delay equations, and we refer the interested reader to Day et al. (2007), Breden et al. (2013), van den Berg et al. (2010), van den Berg et al. (2011), Hungria et al. (2016) and van den Berg et al. (2015) for more discussion and references.

Let us now be more explicit about the above-mentioned resonance conditions (see Sects. 2.2, 2.3 and 2.4 and Cabré et al. 2003a, b, 2005 for full details). We consider a stationary point of an analytic vector field $u^{\prime }=g(u)$, with $u \in \mathbb {R}^n$. Focusing on the stable manifold, we denote the eigenvalues with negative real parts by $\lambda _1,\ldots ,\lambda _d$, where d is the dimension of the manifold. A resonance is a non-trivial relation

$$\begin{aligned} \tilde{k}\cdot \lambda \mathop {=}\limits ^{\text{ def }}\tilde{k}_1 \lambda _1 + \tilde{k}_2 \lambda _2 + \cdots + \tilde{k}_d \lambda _d = \lambda _{\tilde{\imath }}, \end{aligned}$$

for some $\tilde{\imath }\in \{1,\ldots ,d\}$ and $\tilde{k}_i \in \mathbb {N}$ for $i=1,\ldots ,d$. The trivial, excluded case is $\tilde{k}=e_{\tilde{\imath }}$, where we use the notation $e_i$ for the i-th unit vector. If there are no resonances between the stable eigenvalues (the “non-resonant” case), then there is an analytic conjugacy between the flow of $u^{\prime }=g(u)$ on the local stable manifold and the linear flow $\theta _i^{\prime }=\lambda _i \theta _i$, $i=1,\ldots ,d$. Since the conjugacy map $u=P(\theta )$ is analytic, P can be written as a convergent power series in $\theta$.

When there is a resonance between the stable eigenvalues, the conjugacy map P as constructed above is no longer analytic and cannot be expressed as a convergent power series. One way to resolve this obstacle is to change the flow $\theta ^{\prime }=h(\theta )$ in parameter space to a nonlinear “normal form,” in such a way that the conjugacy is again analytic. In this paper we consider two types of resonances in particular, namely the co-dimension one resonances. The first type of resonance is a single “regular” resonance $\tilde{k}\cdot \lambda = \lambda _{\tilde{\imath }} \in \mathbb {R}$ for some $1 \le \tilde{\imath }\le d$ and $\tilde{k}\in \mathbb {N}^d$ with $\sum _{i=1}^d \tilde{k}_i \ge 2$, and no other resonances. The second type is a double real eigenvalue ($\tilde{k}=e_i$ for some $i \ne \tilde{\imath }$) with geometric multiplicity one, and no other resonances. We note that a double eigenvalue is not a resonance in the strict sense, but we nevertheless use this “uniform” terminology in the current paper. These are the only co-dimension one resonances; hence, they are the types that are encountered generically in one-parameter continuation. For this reason we restrict our attention to these resonance types as our examples. We note that a completely analogous approach works for resonances of higher co-dimension, but here omit the details.

In order to illustrate the application of our methods we discuss three example problems in detail. First we analyze the stable manifold of the origin in the well-known Lorenz equations. We use this model system to scrutinize our method in the non-resonant case and show how the structure of the vector field is directly reflected in the bounds used for validation. Second we tune the parameter in the Lorenz system to obtain double stable eigenvalues at the origin to showcase our method in this context.

In the final example the validated computation of stable and unstable manifolds is used as ingredient for the rigorous computation of connecting orbits. In particular we consider also the case of regular resonant eigenvalues. Specifically we compute connecting orbits in the system

$$\begin{aligned} \left\{ \begin{array}{rl} u^{\prime \prime } &{}= -\frac{1}{4} \gamma u-\frac{\sqrt{2}}{4}v^{2} + \frac{3}{8}u^{3}+3uv^{2},\\ v^{\prime \prime } &{}= -\gamma v -\frac{\sqrt{2}}{2} uv +9v^{3} + 3u^{2}v, \end{array}\right. \end{aligned}$$

(1)

which arises as amplitude equations for the pattern formation model

$$\begin{aligned} \partial _{t} U = -(1+\Delta )^2 U +\mu U -\beta \left| \nabla U\right| ^2 -U^3, \end{aligned}$$

(2)

as shown in Doelman et al. (2003). Here $U = U(t,x)$, $t\ge 0$ and $x\in {\mathbb {R}}^2$. Equation (2) arises in the study of the interplay between trivial, hexagonal and roll patterns near the onset of instability of the zero solution. The parameters $\gamma ,\mu$ and $\beta$ are related via $\gamma = \frac{\mu }{\beta ^2}$. See Doelman et al. (2003) and van den Berg et al. (2015) for further details for the relation between (1) and (2).

Following the approach of van den Berg et al. (2015) we prove the existence of a heteroclinic connection between the hexagon and ground states. The proof is based on rigorous numerics for a boundary value problem, where the validated manifolds are used to formulate the boundary conditions. We settle a case left open in van den Berg et al. (2015) due to the presence of resonances in the stable eigenvalues at the origin. In Fig. 1 we depict the verified connecting orbit of (1) as well as the corresponding stationary transition layer between hexagonal spots and the uniform state of (2).

Fig. 1

Left co-existing hexagonal and trivial patterns in (2) for $\beta =1$ and $\mu =-\frac{2}{135}$. Right corresponding connecting orbit in (1) with u and v components in red and blue, respectively (Color figure online)

We remark that an interesting future extension of this work would be to apply the ideas developed here to the validated computation of local stable/unstable manifolds of periodic orbits. The parameterization method has already been adapted to this context. See Guillamon and Huguet (2009), Huguet and de la Llave (2013) and Castelli et al. (2015) for more details and numerical examples. Using the techniques of the present work it should be possible to validate these computations even in the presence of a resonance between the Floquet multipliers. This will be the subject of a future study.

Finally we remark that the references mentioned in this introductory discussion are far from exhaustive, and a comprehensive overview of the literature is beyond the scope of the present work. In recent years a number of authors have developed numerical validation procedures which provide mathematically rigorous a posteriori error bounds on approximations of invariant manifolds associated to various kinds of invariant sets. We refer the interested reader to CAPD (2015), Capinksi and Simo (2012), Johnson and Tucker (2011), Wittig et al. (2010) and Wittig (2011) for fuller discussion of methods other than those presented here.

The outline of the paper is as follows. Section 2 is dedicated to the description of the general setup of our approach. In Sect. 3 we give more details on how we derive the zero finding problem. In Sect. 4 we transform it to an equivalent local fixed point problem to be solved by a parametrized Newton–Kantorovich-type argument. In Sect. 5 we illustrate the performance of our method with the three examples described above. The code implementing these examples can be found at the webpage Code page (2015).

2 Setup

We consider the validated computation of a parametrization of the local stable manifold of a hyperbolic fixed point $p\in {\mathbb {R}}^{n}$ of a dynamical system induced by a nonlinear ODE

$$\begin{aligned} u^{\prime } = g(u)\quad \quad g:{\mathbb {R}}^{n}\rightarrow {\mathbb {R}}^{n} \end{aligned}$$

(3)

using the parametrization method developed in Cabré et al. (2003a, b, 2005). Local unstable manifolds can be obtained by replacing g with $-g$. We assume that g is analytic, allowing us to look for parametrizations in the analytic category. In particular we assume that g is locally (near p) analytically extendable to the complex plane. As a consequence the coefficients in the power series expansion of the parametrization decay geometrically, at an a priori unknown rate. We come back to the role of this decay rate later, see Remark 2.1 and in particular Sects. 5.1.1 and 5.1.2.

2.1 The Invariance Equation

We denote by $\lambda _1,\ldots ,\lambda _d$ the eigenvalues with negative real part of the Jacobian Dg(p) at the fixed point p. To fix notation, let there be s pairs of complex conjugate eigenvalues $\lambda _1,\lambda _2,\ldots ,\lambda _{2s-1},\lambda _{2s}$ with negative real part and $d-2s$ real negative eigenvalues $\lambda _{2s+1},\ldots ,\lambda _d$. The corresponding (generalized) eigenvectors are denoted by $\xi _1, \ldots , \xi _d$. We do not assume that the algebraic multiplicity of the eigenvalues is one. For simplicity, in this paper we assume p, $\lambda _i$ and $\xi _i$ to be a priori determined analytically. However, it is straightforward to append equations for the equilibrium, as well as for the linearization around it, to the computational part of the analysis.

We call the set of stable eigenvalues non-resonant if for every $i=1,\ldots ,d$

$$\begin{aligned} k \cdot \lambda \ne \lambda _i \end{aligned}$$

(4)

for all $k = (k_1,\ldots ,k_d) \in \mathbb {N}^d$ with $k \ne e_i$ (the i-th unit vector). We shall use the notation

$$\begin{aligned} |k| \mathop {=}\limits ^{\text{ def }}\sum _{i=1}^d k_i. \end{aligned}$$

As a new feature of the present work in comparison with the analysis in van den Berg et al. (2011), Mireles-James and Mischaikow (2013) and Mireles-James (2015) we are able to incorporate resonant cases directly in our novel framework for solving and validating the parametrization of the (un)stable manifold. In particular, we focus on the two types of co-dimension one resonances, namely a single regular resonance and an algebraically double, geometrically simple eigenvalue. We have a regular resonant case when

$$\begin{aligned} \tilde{k}\cdot \lambda = \lambda _{\tilde{\imath }} \end{aligned}$$

(5)

for some $\tilde{\imath }\in \{1,\ldots ,d\}$ and a $\tilde{k}\in {\mathbb {N}}^{d}$ with $|\tilde{k}|\ge 2$. We work out in detail the cases where a regular resonance occurs as the only resonance, and where a double real eigenvalue occurs as the only resonance. In both cases, in the co-dimension one situation, the resonant eigenvalue is real valued. Higher co-dimension resonances, in particular multiple or simultaneous resonances (combinations of regular resonances and/or eigenvalues with higher multiplicity), can be dealt with analogously in our general framework.

In the parametrization method one looks for a map P that conjugates the flow of (3) on the stable manifold to a d-dimensional flow $\theta ^{\prime }=h(\theta )$ for a suitably simple choice of h. Specifically, let $P: {\mathbb {C}}^{d}\supset \mathbb {B}_{\nu }\rightarrow {\mathbb {C}}^{n}$ be analytic on the complex polydisc

$$\begin{aligned} \mathbb {B}_{\nu } \mathop {=}\limits ^{\text{ def }}\left\{ z\in \mathbb {C}^{d}: |z_i|\le \nu _i\right\} , \end{aligned}$$

(6)

where $\nu =(\nu _1,\ldots ,\nu _d)$ with $\nu _{i}>0$. We commonly refer to its domain as the parameter space. In particular, the map P possesses a d-variate series expansion

$$\begin{aligned} P(\theta ) = \displaystyle \sum _{|k| = 0}^{\infty }a_{k}\theta ^{k} \end{aligned}$$

(7)

with $a_{k} = (a^{1}_{k},\ldots ,a^{n}_{k})\in \mathbb {{\mathbb {C}}}^{n}$ for $|k|\ge 0$. We use the usual multi-index notation, where for $k = (k_1,\ldots ,k_d)$ we set $\theta ^{k} = \theta _1^{k_1}\ldots \theta _d^{k_d}$. The invariance equation for P is given by

$$\begin{aligned} g(P(\theta )) = DP(\theta )h(\theta ),\qquad \theta \in \mathbb {B}_{\nu }. \end{aligned}$$

(8)

Additionally and without loss of generality, we prescribe the linear constraints

$$\begin{aligned} a_0= & {} p \end{aligned}$$

(9a)

$$\begin{aligned} a_{e_i}= & {} \xi _i \qquad \text {for } \,i=1,\ldots ,d. \end{aligned}$$

(9b)

Remark 2.1

Note that the choice of the eigenvectors $\xi _{i}$ $(i = 1,\ldots ,d)$ is not unique.

In Lemmas 2.2, 2.3 and 2.5 we analyze the relation between the domain radius $\nu$ in (8) and the lengths $\Vert \xi _{i}\Vert$. It will turn out that from a numerical perspective we can either vary $\nu$ or $\Vert \xi _{i}\Vert$. See Remarks 5.1, 5.2 and Breden et al. (2015), Falcolini and de la Llave (1992) and Cabré et al. (2003a) for a more thorough discussion of this topic.

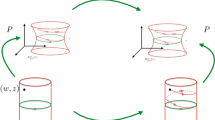
Concerning the choice for the general polynomial normal form of $h(\theta )$ in (8), note that in the non-resonant and double eigenvalue case it is sufficient to use information on the eigenvalues $\lambda _1, \ldots \lambda _d$ to do so. In the resonant case we choose a polynomial ansatz informed by spectral information but solve for the corresponding coeffient [$\tau$ in (27)]. In all cases we shall choose it such that the origin is a (globally) attracting sink in parameter space. We will also see that we can find a subset $\mathbb {B}_{\hat{\nu }} \subset {\mathbb {B}}_\nu$ such that the orbits under the flow $\theta ' = h(\theta )$ of initial data in $\mathbb {B}_{\hat{\nu }}$ do not leave ${\mathbb {B}}_\nu$. We establish the explicit relation between $\nu$ and $\hat{\nu }$ in the three cases under consideration in Lemma 2.7. By the conjugation property of P and (9a), a suitable real-valued restriction (see below) of the image of $\mathbb {B}_{\hat{\nu }}$ under P thus gives us a parametrization of the local stable manifold $W^{s}(p)$. We explain the conjugacy of the flows in Sect. 2.5.

Let us describe how we can define a real-valued parametrization of the stable manifold starting with a complex valued solution of (8) fulfilling (9). Recall that $\lambda =(\lambda _1,\ldots ,\lambda _{2s},\lambda _{2s+1}\ldots \lambda _d)$ consists of s pairs of complex conjugate eigenvalues and $d-2s$ real eigenvalues. We introduce the involutory permutation matrix $\sigma _s$ of the form

$$\begin{aligned} \sigma _s \mathop {=}\limits ^{\text{ def }}\begin{pmatrix} \sigma &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad \ddots &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \sigma &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad I_{d-2s} \end{pmatrix} \in {\mathbb {R}}^{d,d} \qquad \text {with}\qquad \ \sigma = \begin{pmatrix} 0 &{}\quad 1\\ 1 &{}\quad 0 \end{pmatrix}, \end{aligned}$$

(10)

and $I_{d-2s}$ denoting the $d-2s$-dimensional identity matrix. In essence, this involution plays the role of a symmetry. We introduce an involution on d-tuples (including but not limited to $\mathbb {C}^d$, $\mathbb {R}^d$ and $\mathbb {N}^d$) by

$$\begin{aligned} v^* \mathop {=}\limits ^{\text{ def }}\sigma _s \overline{v}, \end{aligned}$$

(11)

where $\overline{v}$ denotes complex conjugation. In particular, we have the involution $k \mapsto k^*$ on $\mathbb {N}^d$. We have ordered the eigenvalues so that $\lambda ^* = \lambda$, and normalized the (generalized) eigenvectors so that $\xi ^* = \xi$. Furthermore, for any variables $q=(q_k)_{k\in \mathbb {N}^d}$ that allow complex conjugation, we denote (again an involution)

$$\begin{aligned} (q^*)_k \mathop {=}\limits ^{\text{ def }}\overline{q}_{k^*}. \end{aligned}$$

(12)

Next, consider the set

$$\begin{aligned} {\mathbb {B}}^{sym }_\nu \mathop {=}\limits ^{\text{ def }}\{ \theta \in {\mathbb {B}}_\nu : \theta ^*= \theta \}, \end{aligned}$$

(13)

for any compatible choice of $\nu \in \mathbb {R}_+^d$, i.e., $\nu ^*=\nu$. The set ${\mathbb {B}}^{sym }_\nu$ is d-dimensional when interpreted as a real linear space (intersected with the ball ${\mathbb {B}}_\nu$), and in the particular case of all eigenvalues being real this boils down to ${\mathbb {B}}^{sym }_\nu = \{ \theta \in \mathbb {R}^d, |\theta _i| \le \nu _i \}$. Moreover, we will find, see Sect. 4, that the coefficients a of P have the symmetry property

$$\begin{aligned} a^* = a. \end{aligned}$$

(14)

Under condition (14) we obtain the following lemma.

Lemma 2.1

Assume (14) to be fulfilled. The map P is real-valued on the invariant subspace ${\mathbb {B}}^{sym }_\nu$.

Proof 2.1

Using the properties of the involution (11) in the second equality, together with $\theta ^* = \theta$ (on ${\mathbb {B}}^{sym }_\nu$) and $a^* = a$ (assumed) in the third, we compute

$$\begin{aligned} \overline{\displaystyle \sum _{k\in {\mathbb {N}}^{d}}a_{k}\theta ^{k}} = \displaystyle \sum _{k\in {\mathbb {N}}^{d}}\bar{a}_{k}\bar{\theta }^{k} = \displaystyle \sum _{k\in {\mathbb {N}}^{d}} a^*_{k^*} {\theta ^{*}}^{k^*} = \displaystyle \sum _{k\in {\mathbb {N}}^{d}} a_{k^*} {\theta }^{k^*} = \displaystyle \sum _{k\in {\mathbb {N}}^{d}} a_{k} {\theta }^{k}, \end{aligned}$$

where the last equality uses the invariance of the summation domain under the involution $^*$. $\square$

Together with Lemma 2.6 which explains the conjugation property of P in more detail, this establishes that P restricted to ${\mathbb {B}}^{sym }_{\hat{\nu }}$ parametrizes the real local stable manifold of p (see Lemma 2.7 for the relation between $\nu$ and $\hat{\nu }$).

Our goal is to compute a numerical approximation of P together with rigorous bounds on the approximation error and its range of validity ${\mathbb {B}}_{\nu }$ by using the method presented in Day et al. (2007). This amounts to first formulating an equivalent zero finding problem on an appropriate Banach space. Second, using an approximate zero, we define a Newton-like fixed point operator T. We establish contractivity of T on a ball around the approximate zero by deriving bounds on the residual, as well as bounds on the derivative that depend polynomially on the radius of the ball. These bounds are used to define so-called radii polynomials as ingredients for a finite set of inequalities encoding the prerequisites for the Banach fixed point theorem. We stress that in this way the radius of the ball on which we obtain contractivity is a variable for which we solve. This is an essential difference of the method in Day et al. (2007) compared to classical Newton–Kantorovich-type arguments. Let us assemble the ingredients to define the zero finding problem.

2.2 Non-resonant Eigenvalues

We distinguish two approaches for solving the invariance equation: the recursive approach and the zero finding approach. The zero finding approach will pave the way to an application of a fixed point argument in the space of power series coefficients. To be concrete, in order to explain the difference between the two approaches, we consider first the case that $\lambda _1,\ldots ,\lambda _d$ are non-resonant. In this case we choose

$$\begin{aligned} h(\theta ) = \Lambda _s \theta , \end{aligned}$$

(15)

where $\Lambda _s$ is the diagonal matrix containing the stable eigenvalues on the diagonal. Clearly, the origin is the global attractor for $\theta ^{\prime }=h(\theta )$. Moreover, $\Lambda _s \sigma _s = \sigma _s \overline{\Lambda _{s}}$, hence $h(\theta ^*)=h(\theta )^*$.

By substituting the series expansion (7) into the invariance Eq. (8), we derive equations for the series coefficients

$$\begin{aligned} a_{k} = (a^{1}_{k},\ldots ,a^{n}_{k})\in \mathbb {Cc}^{n}\quad \text {for}\quad |k|\ge 2. \end{aligned}$$

(16)

This leads to the homological equations for all $|k|\ge 2$:

$$\begin{aligned} \left( Dg(p)- k\cdot \lambda \, I_n\right) a_{k} = b_{k}, \end{aligned}$$

(17)

where $b_k$ only depends on $a_{\hat{k}}$ with $|\hat{k}|<|k|$ and $I_n$ denotes the n-dimensional identity matrix. Note that $b_k$ vanishes for $|k|=1$; hence, (17) reduces to the eigenvalue-eigenvector equation, which is solved by (9b).

Using the initial constraints (9) for $a_{k}$ with $|k|=0,1$ and the fact that $\lambda _1,\ldots ,\lambda _d$ are non-resonant, (17) can be used to compute $a_{k}$ recursively to any desired order ($|k| \le N$). This is what we refer to as the recursive approach. The recursive approach shows that there is (a priori) a unique solution of (8) satisfying the constraints (9), although the decay of the sequence is not guaranteed a priori. The validation in van den Berg et al. (2011), Mireles-James and Mischaikow (2013) and Mireles-James (2015) relies on analysis in function spaces of so-called N-tails.

Equation (17) is derived by writing $g(P(\theta ))$ as a power series expansion in $\theta$ and matching like powers in the left- and right-hand sides of (8). In particular,

$$\begin{aligned} g(P(\theta ))=\sum _{|k|=0}^{\infty } c_k \theta ^k \qquad \text {with}\qquad c_{k} = c_{k}(a) = c_{k}\bigl (\{a_{\hat{k}},\hat{k}\preceq k\}\bigr ), \end{aligned}$$

(18)

where the notation $\hat{k}\preceq k$ means $\hat{k}_i \le k_i$ for $i=1,\ldots ,d$. For later use, we also introduce the notation $\hat{k}\prec k$ for those $\hat{k}\preceq k$ with $\hat{k} \ne k$. Substituting (18) into the invariance Eq. (8) leads to the equations

$$\begin{aligned} c_{k} = (k \cdot \lambda ) \, a_{k}. \end{aligned}$$

(19)

By observing that $b_k$ is defined by the splitting

$$\begin{aligned} c_k=Dg(p)a_k + b_k, \end{aligned}$$

(20)

where $b_k$ depends only on $a_{\hat{k}}$ with $\hat{k}\prec k$, one derives (17). In contrast, in the zero finding approach we omit the splitting (20) and instead interpret (19) as a zero finding problem

$$\begin{aligned} (k \cdot \lambda ) \, a_{k}-c_{k} = 0 \qquad \text {for all } |k| \ge 2 \end{aligned}$$

(21)

on a space of geometrically decaying sequences $\{a_k=(a^1_k,\ldots ,a^n_k)\}_{k\in \mathbb {N}^d}$, see Sect. 3 and also Beyn and Kless (1998) for a related approach.

The recursive approach shows that the initial constraints  (9) for $a_{k}$ with $|k|=0,1$ determine $a_k$ for $|k|\ge 2$ uniquely. While $a_0=p$ is uniquely fixed by the problem at hand, we enjoy the freedom to scale $a_{k}$ for $|k| = 1$ as those are given by the eigenvectors of Dg(p). The following lemma illuminates how such a scaling influences $a_{k}$ for $|k|\ge 2$. Let $\mu \in {\mathbb {C}}^{d}$ be given such that $\mu ^{*} = \mu$. We define the scaling $\mu a \mathop {=}\limits ^{\text{ def }}(\mu ^{k}a_{k})_{k\in {\mathbb {N}}^d}$. In this way scaling preserves the symmetry (14). Moreover, for any analytic nonlinearity g, it follows from the power series representation (18) that

$$\begin{aligned} c_{k}(\mu a) = \mu ^{k} c_{k}(a). \end{aligned}$$

(22)

We have the following invariance of the conjugation map under rescaling by $\mu$.

Lemma 2.2

Let $a = (a_{k})_{k\in {\mathbb {N}}}$ fulfill (9) together with (21) for all $|k|\ge 2$. Then $\mu a$ also solves (21) for all $|k|\ge 2$, whereas $(\mu a)_{e_{i}} = \mu _i \xi _{i}$ for $i = 1,\ldots ,d$.

This follows from (22) and (21). For more detailed discussion see Breden et al. (2015) and also Falcolini and de la Llave (1992) and Cabré et al. (2003a).

We note that the above lemma is equivalent to the observation that the scaling $\theta _i \rightarrow \mu _i \theta _i$ leaves the flow in parameter space invariant, and hence by the conjugacy property, $\mu a$ solves the homological equations whenever a does. In Remark 5.1 we come back to the practical implications of this scaling invariance.

2.3 Double Eigenvalues

We now consider a single repeated (real) eigenvalue with geometric multiplicity one (and no other resonances). Assume without loss of generality that $\lambda _{2s+1} = \lambda _{2s+2}$, with the rest of the eigenvalues being distinct and non-resonant. We choose $\xi _{2s+1}$ to be a (real valued) eigenvector for the double eigenvalue, and $\xi _{2s+2}$ a (real valued) generalized eigenvector such that

$$\begin{aligned}{}[Dg(p) -\lambda _{2s+1} I_n] \xi _{2s+2}=\xi _{2s+1}. \end{aligned}$$

(23)

Furthermore, we choose the flow in parameter space to be (cf. Jordan normal form)

$$\begin{aligned} h(\theta ) = \Lambda _s \theta + \theta _{2s+2} e_{2s+1}, \end{aligned}$$

(24)

so that it is compatible with (23) through (8). Note that in the context of parameter-dependent families of vector fields this approach can be numerically stabilized by using versal transformations, see for example Chow et al. (1994). In the current work no numerical instabilities occur however, as we do not consider continuation problems (although this is the subject of ongoing research).

We observe, again, that the origin is the global attractor for $\theta ^{\prime }=h(\theta )$, and that $h(\theta ^*)=h(\theta )^*$. The corresponding version of (19) is

$$\begin{aligned} c_{k} = (k \cdot \lambda ) \, a_{k} + (k_{2s+1}+1) a_{k+e_{2s+1}-e_{2s+2}}, \end{aligned}$$

(25)

for all $|k| \ge 2$ with $k_{2s+2} \ge 1$. We note that the additional term $(k_{2s+1}+1)a_{k+e_{2s+1}-e_{2s+2}}$ occurs at the same “level of recursion” as the term $a_k$, i.e., $|k+e_{2s+1}-e_{2s+2}| = |k|$. While this necessitates caution in the recursive computation of $a_k$ (which can still be done with the correct ordering), it does not introduce difficulties for our interpretation of (25) as a zero finding problem. Concerning the influence of scaling $a_k$ with $\mu \in {\mathbb {C}}^d$ $(\mu ^*= \mu )$ we obtain the following.

Lemma 2.3

Let $a = (a_{k})_{k\in {\mathbb {N}}^d}$ fulfill (9) together with (25) for all $|k|\ge 2$. Let $\mu \in {\mathbb {C}}^d$ be such that $\mu ^*= \mu$ and $\mu _{2s+1} = \mu _{2s+2}$. Then $\mu a$ also solves (25) for all $|k|\ge 2$, whereas $(\mu a)_{e_{i}} = \mu _i \xi _{i}$ for $i = 1,\ldots ,d$.

Proof 2.2

The proof follows from (25) by noticing that $\mu ^{k+e_{2s+1}-e_{2s+2}} = \mu ^{k}$. $\square$

If one chooses a rescaling with $\mu _{2s+1} \ne \mu _{2s+2}$, the normal form (24) needs to be adapted accordingly.

2.4 Regular Resonant Eigenvalues

As discussed before, the two co-dimension one resonances are the (real) double eigenvalue (Sect. 2.3) and the regular resonant eigenvalue (the other co-dimension one resonance) given by

$$\begin{aligned} \tilde{k}\cdot \lambda = \lambda _{\tilde{\imath }} \end{aligned}$$

(26)

for some $\tilde{\imath }>2s$ (i.e., $\lambda _{\tilde{\imath }}\in \mathbb {R}$) and a $\tilde{k}\in {\mathbb {N}}^{d}$ with $|\tilde{k}|\ge 2$ and $\tilde{k}^*=\tilde{k}$. Here we assume that no other resonances occur.

It follows from the discussion in Sect. 2.2 that for the choice $h(\theta )=\Lambda _s \theta$ the mathematically equivalent recursive and the zero finding approaches are bound to fail. More precisely, assuming (26) to be fulfilled, it is apparent from (17) that the equation for $a_{\tilde{k}}$ is in general not solvable. To resolve this, we modify h to the nonlinear “normal form”

$$\begin{aligned} h(\theta ) = \Lambda _s\theta + \tau \theta ^{\tilde{k}}e_{\tilde{\imath }}, \end{aligned}$$

(27)

where $\tau \in \mathbb {R}$ is to be determined later. This alters (19) for $k \succeq \tilde{k}$ (note that $\tilde{k}_{\tilde{\imath }}=0$) to

$$\begin{aligned} c_{k} = (k \cdot \lambda ) \, a_{k} + \tau (k_{\tilde{\imath }}+1)a_{k+e_{\tilde{\imath }}-\tilde{k}}. \end{aligned}$$

(28)

Note that $|\tilde{k}| \ge 2$ and thus $|k+e_{\tilde{\imath }}-\tilde{k}| = |k|+1-|\tilde{k}| < |k|$. This implies that (28) is amenable to recursive solving for $k \succeq \tilde{k}$, as in the non-resonant case. Obviously, for $k=\tilde{k}$ Eq. (28) can be solved only if $\tau$ satisfies a solvability condition, which will be discussed below. We note that the choice (27) for h represents the simplest effective one. It facilitates an application of bordered matrix techniques (Govaerts 2000) to solve (28) in an efficient way while also providing a means to obtain uniqueness of $a_{\tilde{k}}$, see below. The defining properties of the regular co-dimension one resonance imply that $\tilde{k}^*=\tilde{k}$ and $e_{\tilde{\imath }}^*=e_{\tilde{\imath }}$. Hence, for any $\tau \in \mathbb {R}$ we infer that $h(\theta ^*)=h(\theta )^*$. However, since $\tau$ is a priori unknown, one needs to derive that $\tau$ is real indeed, see Eq. (31).

We now turn our attention to solving (28) for $k=\tilde{k}$. As we will see below, there is a unique $\tau$ making (28) for $k = \tilde{k}$ solvable for $a_{\tilde{k}}$, and by appending a suitable additional constraint we can make this solution unique. Using that $\tilde{k}_{\tilde{\imath }}=0$, we rephrase (28) for $k = \tilde{k}$ as

$$\begin{aligned} \underbrace{(Dg(p)-\lambda _{\tilde{\imath }} I_n)}_{A} a_{\tilde{k}} + \tau a_{e_{\tilde{\imath }}} = b_{\tilde{k}}, \end{aligned}$$

(29)

with $b_{\tilde{k}}$ depending only on $a_{\hat{k}}$ with $\hat{k} \prec \tilde{k}$. Note that by construction $a_{e_{\tilde{\imath }}}\in \ker (A)$, as it is an eigenvector of Dg(p) corresponding to the eigenvalue $\lambda _{\tilde{\imath }}$. The following lemma shows that appending an additional constraint on $a_{\tilde{k}}$ brings about unique solvability of (29) for the pair $(\tau ,a_{\tilde{k}})$.

Lemma 2.4

Let $A \in \mathbb {R}^{n,n}$ have an algebraically simple eigenvalue 0 with eigenvector $\xi$. Let $\zeta \in \mathbb {R}^{n}$, $\zeta \ne 0$ be such that $A^{T}\zeta = 0$. Then $\zeta ^T \xi \ne 0$ and the matrix

$$\begin{aligned} \begin{pmatrix} \xi &{}\quad A \\ 0 &{}\quad \zeta ^{T} \end{pmatrix}\in \mathbb {R}^{n+1,n+1} \end{aligned}$$

is non-singular.

Proof 2.3

The proof of this lemma can, for example, be found in Kuznetsov (2004), p. 174. $\square$

We choose a real vector $\zeta \in \ker (A^T)$. From Lemma 2.4 we see that there is a unique pair $(\tau ,a_{\tilde{k}})$ satisfying

$$\begin{aligned} \begin{pmatrix} a_{e_{\tilde{\imath }}} &{}\quad A \\ 0 &{}\quad \zeta ^{T} \end{pmatrix} \begin{pmatrix} \tau \\ a_{\tilde{k}} \end{pmatrix} = \begin{pmatrix} b_{\tilde{k}}\\ 0 \end{pmatrix}. \end{aligned}$$

This pair $(\tau ,a_{\tilde{k}})$ solves (29), and in addition

$$\begin{aligned} \zeta ^T a_{\tilde{k}} =0. \end{aligned}$$

(30)

Moreover, one derives that

$$\begin{aligned} \tau = \frac{\zeta ^T b_{\tilde{k}}}{\zeta ^T a_{e_{\tilde{\imath }}}}, \end{aligned}$$

(31)

showing that the value of $\tau$ is independent of the choice of $\zeta$. Furthermore, since $b_{k}$ is real for real a by its definition (20), $\tau$ is real whenever a is ($\zeta$ can be chosen to be real valued since $\lambda _{\tilde{\imath }}$ is real). In this case we also obtain a scaling result.

Lemma 2.5

Let $a = (a_{k})_{k\in {\mathbb {N}}}$ fulfill (9) together with (28) for all $|k|\ge 2$ for the unique $\tau$ determined by (31). Let $\mu \in {\mathbb {C}}^{d}$ be such that $\mu ^{*} = \mu$. Then $\mu a$ solves (28) for all $|k|\ge 2$ with $\tau$ replaced by $\tau _\mu =\mu ^{\tilde{k}-e_{\tilde{\imath }}}\tau$, whereas $(\mu a)_{e_{i}} = \mu _i \xi _{i}$ for $i = 1,\ldots ,d$.

Proof 2.4

The proof follows from (28) by using $\mu ^{\tilde{k}-e_{\tilde{\imath }}}\tau (\mu a)_{k-\tilde{k}+e_{\tilde{\imath }}} = \mu ^{k}\tau a_{k-\tilde{k}+e_{\tilde{\imath }}}$.

$\square$

Note that the scaling of $\tau _\mu$ is easily understood by combining (22) with (31). Finally, to a large extent the double eigenvalue case in Sect. 2.3 may be interpreted as a regular resonance with $\tilde{\imath }=2s+1$ and $\tilde{k}=e_{2s+2}$ and $\tau =1$ known a priori (fixed by choosing the standard Jordan normal form).

2.5 Explicit Dynamics in Parameter Space

Let us explain how the invariance Eq. (8) encodes the conjugation of the flows of $u^{\prime } = g(u)$ and $\theta ^{\prime } = h(\theta )$ that we denote by $\Phi (t,u)$ and $\Psi (t,\theta )$ for concreteness. In particular we explain when a restriction to a smaller ball ${\mathbb {B}}_{\hat{\nu }}$ is in order. The following lemma contains the key observation and makes the role of P as a conjugation of flows precise.

Lemma 2.6

Assume $g(P(\theta )) = DP(\theta )h(\theta )$ for $\theta \in {\mathbb {B}}_{\nu }$ and let $\theta \in {\mathbb {B}}_{\nu }$ be chosen such that $\Psi (t,\theta )\in {\mathbb {B}}_{\nu }$ for all $t\ge 0$. Then $u(t)\mathop {=}\limits ^{\text{ def }}P(\Psi (t,\theta ))$ solves $u^{\prime } = g(u), u(0) = P(\theta )$. Furthermore $\Phi (t,P(\theta )) = P(\Psi (t,\theta )))$ and $\lim _{t\rightarrow \infty } u(t)=p$.

Proof 2.5

Let $\theta \in {\mathbb {B}}_{\nu }$ be fixed. Recall that $\frac{d}{dt}\Psi (t,\theta ) = h(\Psi (t,\theta ))$.We compute

$$\begin{aligned} \frac{d}{dt} P(\Psi (t,\theta )) = DP(\Psi (t,\theta ))h(\Psi (t,\theta )) = g(P(\Psi (t,\theta ))), \end{aligned}$$

(32)

where the last equality follows from (8) by the fact that $\Psi (t,\theta )\in {\mathbb {B}}_{\nu }$ for $t\ge 0$.

By definition $u(0) = P(\Psi (0,\theta )) = P(\theta )$ and thus by uniqueness of the solution to the initial value problem $u' = g(u), u(0) = P(\theta )$ we get $g(P(\Psi (t,\theta ))) = \frac{d}{dt}\Phi (t,P(\theta ))$. Together with (32), this yields $\Phi (t,P(\theta )) = P(\Psi (t,\theta )))$ for $t \ge 0$. Since 0 is the global attractor for the flow $\Psi$, we conclude that $\lim _{t\rightarrow \infty } u(t)=\lim _{t\rightarrow \infty } P( \Psi (t,\theta )) =P(0)=p$. $\square$

In resonant cases we may need to restrict $\theta$ to a subset of ${\mathbb {B}}_{\nu }$ to ensure that $P(\theta )\in W^s(p)$. For example, one may choose a smaller ball ${\mathbb {B}}_{\hat{\nu }} \subset {\mathbb {B}}_{\nu }$ to ensure $\Psi (t,\theta )\in {\mathbb {B}}_{\nu }$ for all $\theta \in {\mathbb {B}}_{\hat{\nu }}$ and $t\ge 0$. To be able to formulate a criterion for all three cases simultaneously, we introduce

$$\begin{aligned} \ell _0(y_1,y_2) \mathop {=}\limits ^{\text{ def }}\max \left\{ |y_1|, |y_2| e^{\min \{0, -1+y_1/y_2 \}} \right\} , \end{aligned}$$

(33)

and

$$\begin{aligned} \ell ({\hat{\nu }}) \mathop {=}\limits ^{\text{ def }}{\left\{ \begin{array}{ll} \hat{\nu } &{} \text { for the non-resonant case,} \\ \hat{\nu }+\Bigl [\ell _0\bigl (\hat{\nu }_{2s+1}, \tfrac{\hat{\nu }_{2s+2}}{|\lambda _{2s+1}|}\bigr )-\hat{\nu }_{2s+1}\Bigr ] e_{2s+1} &{} \text { for the double eigenvalue case,}\\ \hat{\nu }+\Bigl [\ell _0\bigl (\hat{\nu }_{\tilde{\imath }}, \frac{|\tau |\hat{\nu }^{\tilde{k}}}{|\lambda _{\tilde{\imath }}|}\bigr )-\hat{\nu }_{\tilde{\imath }}\Bigr ] e_{\tilde{\imath }} &{} \text { for the regular resonant case.} \end{array}\right. } \end{aligned}$$

(34)

The following lemma establishes both a uniform and a pointwise criterion. The former establishes a parametrization of $W^s_{\text {loc}}(p)$, whereas the latter is convenient when analyzing a specific orbit.

Lemma 2.7

Let $g(P(\theta )) = DP(\theta )h(\theta )$ for $\theta \in {\mathbb {B}}_{\nu }$. Let $\ell _0$ and $\ell$ be as defined in (33) and (34).

• (a) For all three cases: if $\ell (\hat{\nu }) \preceq \nu$, then $P({\mathbb {B}}_{\hat{\nu }}) \subset W^s(p)$.

• (b) For the double eigenvalue case: if $\theta \in {\mathbb {B}}_{\nu }$ and $\ell _0\bigl (\theta _{2s+1},\frac{\theta _{2s+2}}{|\lambda |}\bigr ) \le \nu _{2s+1}$, then $P(\theta ) \in W^s(p)$.

• (c) For the regular resonant case: if $\theta \in {\mathbb {B}}_{\nu }$ and $\ell _0\bigl (\theta _{\tilde{\imath }},\frac{\tau \theta ^{\tilde{k}}}{|\lambda _{\tilde{\imath }}|}\bigr ) \le \nu _{\tilde{\imath }}$, then $P(\theta ) \in W^s(p)$.

Proof 2.6

For the non-resonant case this is a direct consequence of Lemma 2.6 and the fact that $\Psi _i(t,\theta )\le \theta _i$ for all $t \ge 0$. For the regular resonant case, the explicit flow for $\theta ^{\prime } = h(\theta )$ is given by

$$\begin{aligned} \Psi (t,\theta ) = \exp (\Lambda _{s}t)\theta + \left( \tau \theta ^{\tilde{k}} t e^{\lambda _{\tilde{\imath }}t}\right) e_{\tilde{\imath }}. \end{aligned}$$

For $i \ne \tilde{\imath }$ we have $|\Psi _i(t,\theta )| \le \theta _i$ for all $t \ge 0$. For the resonant coordinate we infer

$$\begin{aligned} |\Psi _{\tilde{\imath }}(t,\theta )| = | \theta _{\tilde{\imath }} + \tau \theta ^{\tilde{k}} t | e^{\lambda _{\tilde{\imath }}t} \le \ell _0\bigl (\theta _{\tilde{\imath }}, \tfrac{\tau \theta ^{\tilde{k}}}{|\lambda _{\tilde{\imath }}|} \bigr ) \qquad \text {for all } t \ge 0. \end{aligned}$$

This proves part (c) and part (a) for the regular resonant case follows from the inequality $\ell _0(y_1,y_2) \le \ell _0(|y_1|,|y_2|)$. Finally, the proof for the double eigenvalue case follows by putting $\tilde{\imath }=2s+1$, $\tilde{k}=e_{2s+2}$ and $\tau =1$ in the above arguments. $\square$

3 The Zero Finding Problem

In this section we derive the zero finding problem on the space of geometrically decaying series coefficients whose solution corresponds to a solution P of (8) via (7). The functional analytic setup is close to the one utilized in Hungria et al. (2016) with the main difference lying in the convolution structure.

3.1 Spaces and Norms

As we work with analytical parametrizations P of the form (7), we consider the complex sequence spaces

$$\begin{aligned} W^{\nu } \mathop {=}\limits ^{\text{ def }}\{w = (w_{k})_{k\in \mathbb {N}^{d}}, w_k\in \mathbb {C}: \Vert w\Vert _{\nu } \mathop {=}\limits ^{\text{ def }}\displaystyle \sum _{|k| = 0}^{\infty }|w_{k}|\nu ^{k}<\infty \}, \end{aligned}$$

(35)

with $\nu \in \mathbb {R}^d_+$. Note that if $a^j=(a^j_k)_{k \in \mathbb {N}^d} \in W^{\nu }$ for $j=1,\ldots ,n$, then P is well defined in $\mathbb {B}_{\nu }$. If we define for $w,\tilde{w}\in W^{\nu }$ the convolution operation

$$\begin{aligned} (w*\tilde{w})_{k} \mathop {=}\limits ^{\text{ def }}\displaystyle \sum _{\mathop {\hat{k}\in \mathbb {N}^d}\limits ^{\hat{k}\preceq k}} w_{k-\hat{k}} \, \tilde{w}_{\hat{k}}, \end{aligned}$$

(36)

the Banach space $(W^{\nu },\Vert \cdot \Vert _{\nu })$ becomes a Banach algebra with multiplication $*$. In particular,

$$\begin{aligned} \Vert w*\tilde{w}\Vert _{\nu }\le \Vert w\Vert _{\nu } \Vert \tilde{w}\Vert _{\nu }. \end{aligned}$$

Taking scalar constraints necessary in the resonant case into account we define the space

$$\begin{aligned} \mathcal {X}_{l_0}^{\nu } \mathop {=}\limits ^{\text{ def }}\mathbb {C}^{l_0}\times (W^{\nu })^n, \end{aligned}$$

(37)

where $l_0$ denotes the number of extra variables (as well as the number of constraints). In particular $l_0 = 0$ in the non-resonant case and for double eigenvalues, whereas $l_0 = 1$ for (single) regular resonances. We have chosen this somewhat convoluted general notation to deal with all cases in one framework. The notation naturally allows incorporation of multiple (simultaneous) resonances by taking $l_0>1$. We denote elements $x\in \mathcal {X}_{l_0}^{\nu }$ by

$$\begin{aligned} x = (x_{-1},\ldots ,x_{-l_0};x^{1},\ldots ,x^n). \end{aligned}$$

To avoid using projection operators we use the somewhat awkward looking, but compact, notation $\{x_{-l}\}_{l=1}^{l_0}$ for the scalar part of x. We endow $\mathcal {X}_{l_0}^{\nu }$ with the norm

$$\begin{aligned} \Vert x\Vert \mathop {=}\limits ^{\text{ def }}\max \left( \max _{l=1,\dots ,l_0} |x_{-l}|,\max _{j=1,\ldots ,n}\Vert x^{j}\Vert _{\nu }\right) . \end{aligned}$$

(38)

3.2 Zero Finding Problem: Non-resonant Case

We define an operator $f^{\text {nonres}}$ on $\mathcal {X}_{0}^{\nu }$ whose zeros correspond to analytic solutions P of (8) subject to the linear constraints (9). Based on (21), we set

$$\begin{aligned} f^{\text {nonres}}_{k}(x) \mathop {=}\limits ^{\text{ def }}{\left\{ \begin{array}{ll} a_{k}-p &{} k=0\\ a_{k}-\xi _{i} &{} k = e_{i} \quad (i=1,\ldots ,d)\\ \left( k\cdot \lambda \right) a_{k}-c_{k}(a) &{} |k|\ge 2, \end{array}\right. } \end{aligned}$$

(39)

where $x = a$ and $Dg(p)\xi _{i} = \lambda _i\xi _i$. Given a vector field g and once $\Vert \xi _i\Vert$ is chosen, $f^{\text {nonres}}$ is fixed, and via (7) zeros of (39) correspond to a parametrization of the local stable manifold of p.

3.3 Zero Finding Problem: Double Eigenvalue

Based on (25), we define the operator $f^{\text {double}}$ on $\mathcal {X}_{0}^{\nu }$ by

$$\begin{aligned} f^{\text {double}}_{k}(x) \mathop {=}\limits ^{\text{ def }}{\left\{ \begin{array}{ll} a_{k}-p &{} k=0\\ a_{k}-\xi _{i} &{} k = e_{i} \quad (i=1,\ldots ,d)\\ \left( k\cdot \lambda \right) a_{k} - c_k &{} |k|\ge 2 \wedge k_{2s+2}=0\\ \left( k\cdot \lambda \right) a_{k} + (k_{2s+1}+1)a_{k+e_{2s+1}-e_{2s+2}} - c_k(a) &{} |k|\ge 2 \wedge k_{2s+2}\ge 1, \end{array}\right. } \end{aligned}$$

(40)

where $x = a$, and $\xi _i$ are the (generalized) eigenvectors, as discussed in Sect. 2.3.

3.4 Zero Finding Problem: Regular Resonant Case

In the regular resonant case, we choose a setup with $\tau$ as an extra unknown and (30) as appended equation. Based on (28) we define the operator $f^{\text {regres}}$ on $\mathcal {X}_{1}^{\nu }$ by

$$\begin{aligned} f^{\text {regres}}_{k}(x) \mathop {=}\limits ^{\text{ def }}{\left\{ \begin{array}{ll} \zeta ^{T}a_{\tilde{k}} &{} k=-1\\ a_{k}-p &{} k=0\\ a_{k}-\xi _{i} &{} k = e_{i} \quad (i=1,\ldots ,d)\\ \left( k\cdot \lambda \right) a_{k}-c_{k} &{} |k|\ge 2 \wedge k \not \succeq \tilde{k} \\ \left( k\cdot \lambda \right) a_{k} + \tau (k_{\tilde{\imath }}+1)a_{k+e_{\tilde{\imath }}-\tilde{k}} - c_k(a) &{} |k|\ge 2 \wedge k \succeq \tilde{k}, \end{array}\right. } \end{aligned}$$

(41)

where $x = (\tau ;a)$ and $\zeta \in \ker ((Dg(p)-\lambda _{\tilde{\imath }} I_n)^T)$ is fixed (and real valued). We recall that we use negative indices to number scalar constraints; hence, we have slightly abused notation here by using $k=-1$ to denote the scalar part of $f^{\text {regres}}$, whereas everywhere else $k \in \mathbb {N}^d$.

4 Fixed Point Operator and Radii Polynomials

We are now equipped with operators $f^{\text {nonres}}$, $f^{\text {double}}$ and $f^{\text {regres}}$ given by (39) defined on $\mathcal {X}^\nu _0$, (40) defined on $\mathcal {X}^\nu _0$, and (41) defined on $\mathcal {X}^\nu _1$, respectively. We simply use the notation f defined on $\mathcal {X}$ if this does not lead to confusion. The zero of f corresponds to a parametrization of the stable manifold, a fact we still need to make more precise in due course. We follow the setup of Day et al. (2007) and Hungria et al. (2016) and derive an equivalent fixed point operator, whose contractivity on a ball around an approximate solution we establish using the so-called radii polynomials. Similar approaches have been used in previous works such as Eckmann et al. (1984), Arioli and Koch (2010) and Arioli and Koch (2015) and earlier in Lanford (1982). The structure of the fixed point operator $T: \mathcal {X}\rightarrow \mathcal {X}$ is Newton-like, i.e.,

$$\begin{aligned} T(x) \mathop {=}\limits ^{\text{ def }}x-Af(x), \end{aligned}$$

(42)

where A, which is specified below, plays the role of an approximate inverse of $Df(\hat{x})$, with $\hat{x}$ an approximate solution to $f(x) = 0$. We extend the symmetry from Sect. 2.1 to $x \in \mathcal {X}^\nu _{l_0}$ by setting

$$\begin{aligned} x^* \mathop {=}\limits ^{\text{ def }}(\overline{x_{-1}},\ldots ,\overline{x_{-l_0}};(x^1)^*,\ldots ,(x^n)^*). \end{aligned}$$

We define T, and in particular A, in such a way that T allows a well-defined restriction to the closed symmetric subspace $\mathcal {X}^{{sym }}$ given by

$$\begin{aligned} \mathcal {X}^{{sym }} = \mathcal {X}^{\nu ,{sym }}_{l_0} \mathop {=}\limits ^{\text{ def }}\{x \in \mathcal {X}: x^{*}=x \} \cong \mathbb {R}^{l_0} \times (W^{\nu ,{sym }})^n, \end{aligned}$$

(43)

where

$$\begin{aligned} W^{\nu ,{sym }} = \{w \in W^{\nu } : w^{*}=w \}. \end{aligned}$$

(44)

The function f defined in the three cases (39), (40) and (41) respects the symmetry.

Lemma 4.1

We have $f(x^*) = f(x)^*$.

Proof 4.1

We start by showing that $c(a^*)=c(a)^*$. The vector field $u^{\prime }=g(u)$ is real; hence $g(\overline{u})=\overline{g(u)}$. Considering the definition (18) of c(a), we will exploit the identity $g(\overline{P(a,\theta )})=\overline{g(P(a,\theta ))}$, where we write $P(\theta )=P(a,\theta )$ for clarity. We first observe, by using that the summation domain is invariant under the involution $k \mapsto k^*$, that

$$\begin{aligned} \overline{P(a,\theta )} = \sum _{k \in \mathbb {N}^d} \overline{a}_k \overline{\theta }^k = \sum _{k \in \mathbb {N}^d} (a^*)_{k^*} (\theta ^*)^{k^*} = \sum _{k \in \mathbb {N}^d} (a^*)_k (\theta ^*)^k = P(a^*,\theta ^*). \end{aligned}$$

It follows that

$$\begin{aligned} g(\overline{P(a,\theta )})= g(P(a^*,\theta ^*))= \sum _{k \in \mathbb {N}^d} c(a^*)_k (\theta ^*)^k. \end{aligned}$$

(45)

On the other hand

$$\begin{aligned} \overline{g(P(a,\theta ))} = \sum _{k \in \mathbb {N}^d} \overline{c(a)}_k \overline{\theta }^k = \sum _{k \in \mathbb {N}^d} \overline{c(a)}_{k^*} \overline{\theta }^{k^*} = \sum _{k \in \mathbb {N}^d} c(a)^*_{k} (\theta ^*)^k. \end{aligned}$$

(46)

By combining (45) and (46) we infer that

$$\begin{aligned} \sum _{k \in \mathbb {N}^d} c(a^*)_k (\theta ^*)^k = \sum _{k \in \mathbb {N}^d} c(a)^*_k (\theta ^*)^k. \end{aligned}$$

It follows from uniqueness of the Taylor coefficients that $c(a^*)=c(a)^*$. Using that $\overline{(k\cdot \lambda )} = k^*\cdot \lambda$ this proves the assertion for the non-resonant case. Additionally, for the case of double eigenvalue and regular resonant cases we observe that the conditions $k_{2s+2} \ge 1$ and $k \succeq \tilde{k}$ are invariant under the involution, since $k^*_i = k_i$ for $i>2s+1$ and $\tilde{k}^*=\tilde{k}$. Finally, the symmetry of the scalar part $f_{-1}$ in (41) follows from $\overline{\zeta }=\zeta$ and $\tilde{k}^*=\tilde{k}$. $\square$

We now can make the correspondence between zeros of f and parametrizations of local stable manifolds more precise.

Lemma 4.2

If $f(x) = 0$ for $x\in \mathcal {X}^{\nu }_{l_0}$, then $x^* = x$. In particular $a= (x^{1},\ldots ,x^{n})$ defines via (7) a parametrization $P:{\mathbb {B}}_{\hat{\nu }}\rightarrow {\mathbb {R}}^{n}$ of the local stable manifold of p provided $\hat{\nu }$ and $\nu$ satisfy the condition $\ell (\hat{\nu }) \preceq \nu$ in Lemma 2.7a.

Proof 4.2

Assume $f(x) = 0$. Then using Lemma 4.1

$$\begin{aligned} f(x^*) = f(x)^* = 0^* = 0. \end{aligned}$$

By uniqueness of zeros of f it follows that $x^* = x$. By construction of f in (39), (40) or (41), P defined through a via (7) solves (8) under the constraints (9a) and (9b) with h specified by (15), (24) or (27), respectively. Hence the statement follows by combining Lemmas 2.1 and 2.6. $\square$

To define the linear operator A that appears in (42), we start by defining a finite dimensional projection $\pi _{m}$ on $\mathcal {X}$. For $m = (m_1,\ldots ,m_d)$, we introduce the index set

$$\begin{aligned} {\mathcal {I}}_m\mathop {=}\limits ^{\text{ def }}\{-1,\ldots ,-l_0 \} \sqcup \{ k\in \mathbb {N}^d : k \preceq m \}. \end{aligned}$$

(47)

Note that we require $m^* = m$ in the case of s complex conjugate eigenvalue pairs, so that $k\in {\mathcal {I}}_m$ if and only if $k^*\in {\mathcal {I}}_m$. Using this notation we set

$$\begin{aligned} \pi _{m}x \mathop {=}\limits ^{\text{ def }}(x_k)_{k\in {\mathcal {I}}_m}. \end{aligned}$$

The range of $\pi _m$ can be identified with $\mathbb {C}^M$ where $M = l_0 + n \prod _{i=1}^{d}(m_i+1)$. The symmetry operation descends to an involution $\Sigma _s$ on $\mathbb {C}^M$ through

$$\begin{aligned} \Sigma _s \pi _m(\overline{x})\mathop {=}\limits ^{\text{ def }}\pi _m(x^*). \end{aligned}$$

(48)

An element $x_F$ in the range of $\pi _m$ can be lifted to $\mathcal {X}$ through the trivial embedding

$$\begin{aligned} (\iota x_F )_k \mathop {=}\limits ^{\text{ def }}{\left\{ \begin{array}{ll} (x_F)_k &{} k\in {\mathcal {I}}_m\\ 0 &{} k\notin {\mathcal {I}}_m\end{array}\right. } \end{aligned}$$

(49)

We define the “Galerkin” projection

$$\begin{aligned} f^m(x_F) \mathop {=}\limits ^{\text{ def }}\pi _m f(\iota x_F). \end{aligned}$$

We now assume an approximate zero $\widehat{x}_F$ of $f^m$ has been computed (e.g., using a standard Newton method), and that $A_m$ is a numerical approximation of the inverse of the Jacobian, i.e., $A_m \approx (Df^{m}(\widehat{x}_{F}))^{-1}$. We denote by $A_m^s \mathop {=}\limits ^{\text{ def }}\frac{1}{2}\left( A_{m} + \Sigma _s\overline{A_m}\Sigma _s\right)$ its symmetrized version, which has the property

$$\begin{aligned} A_m^s\Sigma _s = \Sigma _s \overline{A_m^s}. \end{aligned}$$

(50)

Remark 4.1

Since in practice $\widehat{x}_F^* \approx \widehat{x}_F$, it follows from $f(x^*)=f(x)^*$ that $A_m^s \approx A_m$. Consequently, $A_m^s Df^m(\widehat{x}_F) \approx I_M$. Furthermore, replacing $A_m$ by its symmetrization $A_m^s$ is not strictly necessary, since the symmetry of the fixed point, derived in Lemma 4.5 below, can also be obtained from the a priori uniqueness through Lemma 4.2.

We define the linear operator A by

$$\begin{aligned} (Ax)_{k} \mathop {=}\limits ^{\text{ def }}{\left\{ \begin{array}{ll} (A_{m}^{s}\pi _{m}x)_{k} &{} k\in {\mathcal {I}}_m, \\ \frac{1}{\lambda _1 k_1+\ldots +\lambda _dk_d}x_{k} &{} k\notin {\mathcal {I}}_m. \end{array}\right. } \end{aligned}$$

(51)

By construction, A conserves the symmetry, as expressed by the following lemma.

Lemma 4.3

Let A be defined by (51). Then $Ax^*=(Ax)^*$.

Proof 4.3

Since $m^*=m$ and $\lambda ^*=\lambda$, it follows that $(Ax^*)_k=((Ax)^*)_k$ for $k \notin {\mathcal {I}}_m$. It remains to establish that $A_m^s x_F^* = (A_m^s x_F)^*$, which follows from (48) and (50). $\square$

Lemma 4.4

We have $T(x^*)=T(x)^*$. In particular, T maps $\mathcal {X}^{sym }$ into itself.

Proof 4.4

This follows directly from Lemmas 4.1 and 4.3. $\square$

We aim to show that T is contraction on a small ball around an approximate zero $\widehat{x}=\iota \widehat{x}_F \in \mathcal {X}$. It follows from Lemma 4.5 that if $\widehat{x}$ is symmetric ($\widehat{x}^* = \widehat{x}$) or almost symmetric, then the unique fixed point of T in the ball is a symmetric zero of f (provided A is injective).

Lemma 4.5

Assume that T is a contraction on the ball $B_{\widehat{x}}(r)$ with $B_{\widehat{x}}(r)\cap \mathcal {X}^{sym }\ne \emptyset$. Then T has a unique fixed point $\widetilde{x}$ in $B_{\widehat{x}}(r)$, and $\widetilde{x}^*=\widetilde{x}$. If, in addition, $A_m^s$ is invertible, then $\widetilde{x}$ is a zero of f, and hence corresponds a parametrization of the real stable manifold.

Proof 4.5

The first part follows from the Banach fixed point theorem. Since T leaves $\mathcal {X}^{{sym }}$ invariant, T is a contraction mapping on $B_{\widehat{x}}(r)\cap \mathcal {X}^{{sym }}\ne \emptyset$, hence its fixed point lies in $\mathcal {X}^{{sym }}$. If $A_m^s$ is injective, then the fixed point $\widetilde{x}$ corresponds to a zero of f, and the rest of the proof follows directly from Lemma 4.2. $\square$

As explained in Remark 4.1, the assertions of Lemma 4.5 also hold if one replaces $A_m^s$ by its unsymmetrized analogue $A_m$, provided it is invertible. We now describe how we show the contractivity of T on a suitable ball. Let us introduce the operator $A^{\dag }$ given by

$$\begin{aligned} (A^{\dag }x) \mathop {=}\limits ^{\text{ def }}{\left\{ \begin{array}{ll} (Df^{m}(\widehat{x}_{F})\pi _{m}x)_{k} &{} k\in {\mathcal {I}}_m\\ \left( \lambda _1 k_1+\ldots +\lambda _dk_d\right) a_{k} &{} k\notin {\mathcal {I}}_m, \end{array}\right. } \end{aligned}$$

(52)

which acts as an approximation to the derivative of f at $\iota \widehat{x}_F$. Note that in particular $AA^{\dag }\approx \text {Id }$. For later use we note that DT(x)y can be split as

$$\begin{aligned} DT(x)y = (\text {Id }-ADf(x))y = (\text {Id }-AA^{\dag })y-A(Df(x)y-A^{\dag }y). \end{aligned}$$

(53)

Here $\text {Id }$ denotes the identity on $\mathcal {X}$. We continue by defining bounds that will be used to prove contractivity of T.

Definition 4.1

Let $\widehat{x}=\iota \widehat{x}_F\in \mathcal {X}$ be given. Let $Y=(Y_{-1},\ldots ,Y_{-l_0};Y^1,\ldots ,Y^n) \in \mathbb {R}^{l_0+n}_+$ be bounds such that

$$\begin{aligned} |(T(\hat{x})-\hat{x})_{-l}|\le & {} Y_{-l} \qquad \text {for }l=1,\ldots ,l_0 \end{aligned}$$

(54a)

$$\begin{aligned} \Vert (T(\hat{x})-\hat{x})^{j}\Vert _\nu\le & {} Y^j \,\,\qquad \text {for }j=1,\ldots ,n. \end{aligned}$$

(54b)

Let $Z(r)=(Z_{-1}(r),\ldots ,Z_{-l_0}(r);Z^1(r),\ldots ,Z^n(r))$ be $l_0+n$ polynomials in r with nonnegative coefficients, such that for all v, w with $\Vert v\Vert \le 1$ and $\Vert w\Vert \le 1$ the following bounds hold for all $r \ge 0$:

$$\begin{aligned} |(DT(\hat{x}+rv)rw)_{-l}|\le & {} Z_{-l}(r) \qquad \text {for }l=1,\ldots ,l_0 \end{aligned}$$

(55a)

$$\begin{aligned} \Vert (DT(\hat{x}+rv)rw)^{j}\Vert _\nu\le & {} Z^{j}(r) \,\,\,\qquad \text {for }j=1,\ldots ,n. \end{aligned}$$

(55b)

We define the radii polynomials by

$$\begin{aligned}&p_{-l}(r) \mathop {=}\limits ^{\text{ def }}Y_{-l}+Z_{-l}(r)-r \qquad \text {for }l=1,\ldots ,l_0 \end{aligned}$$

(56a)

$$\begin{aligned}&p^{j}(r) \mathop {=}\limits ^{\text{ def }}Y^{j}+Z^{j}(r)-r \,\,\quad \qquad \text {for }j=1,\ldots ,n, \end{aligned}$$

(56b)

and set $p(r) = (p_{-l_0}(r),\ldots ,p_{-1}(r),p_1(r),\ldots ,p_{n}(r))$.

The crux of this definition is that the bounds Y on the residue and Z on the derivative of T can be constructed explicitly, see the examples in Sect. 5. We note that the inclusion of the scalar r in (55) trivially scales the bounds on DT by a factor r. We include this factor here to keep the notation compatible with earlier papers (going back to Yamamoto 1998). The radius r of the ball is not fixed a priori and the $l_0+n$ radii polynomials p(r) are used in the following parametrized version of the Newton–Kantorovich theorem.

Lemma 4.6

Let $r>0$ be such that $p_{-l}(r)<0$ for $l=1,\ldots ,l_0$ and $p^{j}(r)<0$ for $j=1,\ldots ,n$. Then T is a contraction on $B_{\widehat{x}}(r)$ and there is a unique fixed point $\tilde{x} \in B_{\widehat{x}}(r)$ of T.

A proof of this lemma can be found, e.g., in Yamamoto (1998), Day et al. (2007) and Hungria et al. (2016).

Remark 4.2

We emphasize two consequences.

• 1. The $l_0+n$ conditions $p(r)<0$ reduce the validation of zeros of the operators f defined on the infinite dimensional spaces $\mathcal {X}$ to a finite set of inequalities that can be checked rigorously using interval arithmetic. Note that the inequality $p(r)<0$ is to be understood component-wise.

• 2. We can translate $p(r)<0$ to a statement about the error of the image of the parametrization in phase space. Denote by $P_m(\theta ) = \sum _{k\in {\mathcal {I}}_m}\widehat{a}_k\theta ^{k}$ the approximate parametrization corresponding to $\widehat{x}$, and by $P (\theta )= \sum _{k\in \mathbb {N}^d}\widetilde{a}_k\theta ^{k}$ the exact parametrization corresponding to $\widetilde{x}$. Then for all $\theta \in {\mathbb {B}}^{sym }_{\nu }$ and all $j=1,\ldots ,n$

  $$\begin{aligned} |P^j(\theta )-P^j_m(\theta )| \le \sum _{k \in \mathbb {N}^d} |\widetilde{a}^j_{k}-\widehat{a}^j_k| |\theta ^{k}| \le \Vert \widetilde{a}^j-\widehat{a}^j\Vert _\nu \le \Vert \widetilde{x}-\widehat{x}\Vert \le r. \end{aligned}$$

  (57)

• 3. Another consequence is that

  $$\begin{aligned} |\widetilde{a}_{k}^{j}|\le \frac{r}{\nu ^{k}} \qquad \text {for all } k\notin {\mathcal {I}}_m\quad \text { and } \quad j = 1,\ldots , n. \end{aligned}$$

  (58)

  This gives control over the tail coefficients in the exact parametrization. Note that it is this information that is crucial to the method in van den Berg et al. (2011) for deriving a posteriori bounds on the derivative of the truncation error in the parametrization (see van den Berg et al. (2011), Section 5.2, Eqn. (87)). As a consequence, the analysis in van den Berg et al. (2011) is applicable with the radius r obtained from the current approach.

To derive the bounds (54) and (55) good analytical control on the operator f and its derivative Df at $\widehat{x}$ is essential. In Sects. 5.1 and 5.2 we illustrate the “mechanics” involved in the derivation of these bounds.

5 Applications

In this section we consider three applications to illustrate the performance of our method. We start with the well-known Lorenz equations and compute a 2D local stable manifold at the classical parameter values yielding non-resonant eigenvalues. Subsequently, we consider non-standard parameter values in the Lorenz system to investigate the specific issues in the double eigenvalue case. Finally we consider the case of regular resonant eigenvalues in a system of ODEs originating from a pattern formation model. We compute (un)stable manifolds that serve as ingredient for a connecting orbit computation in this system.

5.1 Local Manifolds in the Lorenz System

We consider the Lorenz differential equations (Lorenz 1963)

$$\begin{aligned} \dot{u} = g(u) = \begin{pmatrix} \sigma (u_2-u_1)\\ \rho u_1-u_2-u_1u_3\\ u_1u_2-\beta u_3 \end{pmatrix}. \end{aligned}$$

(59)

In Sect. 5.1.1 we choose the classical parameter values $\beta = \frac{8}{3}$ and $\sigma = 10$ and $\rho = 28$ and describe the validation process including the derivation of the necessary bounds for the 2D local stable manifold of the origin (local Lorenz manifold) in some detail. In particular, we investigate how to choose the various computational parameters involved in the validation process taking different objectives into account. In Sect. 5.1.2 we use the fact that we have explicit formulas for the stable eigenvalues at the origin to tune the parameters $\beta ,\rho ,\sigma$ such that there are double eigenvalues at the origin. We explain the validation analysis in this context, which serves as preparation for the regular resonant case.

5.1.1 Detailed Analysis for the Local Lorenz Manifold: Non-resonant Eigenvalues

The dimension of the manifold is $d = 2$, and the phase space dimension is $n = 3$. Denote the stable eigenvalues by $\lambda _{1,2}$ and the corresponding eigenvectors by $\xi _{1,2}$. As a matter of fact $\lambda _{1,2}\in {\mathbb {R}}$. Hence, we search for a map $P: \mathbb {R}^{2}\supset \mathbb {B}_{\nu }\rightarrow \mathbb {R}^{3}$ together with $\nu = (\nu _1,\nu _2)$ fulfilling (8), with g given by the Lorenz vector field (59), and the linear constraints (9). As we are in the non-resonant case we can choose $\nu = \hat{\nu }$ as discussed in Sect. 2.5. We make the power series ansatz (7) with $a_{k} = (a_{k_1 k_2}^{1},a_{k_1 k_2}^{2},a_{k_1 k_2}^{3})\in \mathbb {R}^{3}$. Note that the coefficients $c_{k} = (c_{k_1k_2}^{1},c_{k_1k_2}^{2},c_{k_1k_2}^{3})$ in the expansion (18) are

$$\begin{aligned} c_{k_1 k_2} = \begin{pmatrix} \sigma \left( a_{k_1 k_2}^{2}-a_{k_1 k_2}^{1}\right) \\ \rho a_{k_1 k_2}^{1} - a_{k_1 k_2}^{2} - (a^{1}*a^{3})_{k_1 k_2}\\ (a^{1}*a^{2})_{k_1 k_2} - \beta a^{3}_{k_1 k_2} \end{pmatrix} \end{aligned}$$

(60)

with $*$ defined in (36). Together with $p = 0\in \mathbb {R}^3$ this completes the ingredients for $f^{\text {nonres}}$ defined in (39).

Recalling the definition of the radii polynomials in (56b), we notice that a necessary condition for finding a radius r fulfilling $p^{i}(r)<0$ for $i=1,2,3$ is that the components of $Z_{1}$ derived in (65) be smaller than one. The parameters that are under our direct control are $m = (m_1,m_2)$ and $\nu = (\nu _1,\nu _2)$ or $\Vert \xi _{1,2}\Vert$, respectively. Note that varying $\nu _{1,2}$ is in the following precise sense equivalent to varying $\xi _{1,2}$, which implies that we may as well fix either $\nu$ or $\xi$.

Remark 5.1

From the scaling operation analyzed in Lemma 2.2, we notice that

$$\begin{aligned} \Vert \mu a^j \Vert _{\nu } = \Vert a^j\Vert _{\mu \nu }, \qquad j=1,2,3. \end{aligned}$$

This implies that we should either vary the decay rates (domain radius) $\nu$ or the (eigenvector) scalings $\mu$ to affect $\Vert \hat{a}^{j}\Vert _{\nu }$, $j = 1,2,3$ in $Z_1$. Below we fix $\nu = (1,1)$, as this is numerically the most stable choice.

Let us describe the dependence of the coefficients of $p^i(r)$ on these computational parameters in more detail by deriving explicit formulas for the radii polynomials.

Derivation of the bounds: details To define the radii polynomials specified in (56b) we first need to compute the bounds $Y^j$ and $Z^j$ $(j = 1,2,3)$ defined in (54) and (55). Assume we have already calculated an approximate zero $\hat{x} = (\hat{a}^{1},\hat{a}^{2},\hat{a}^{3}) = \iota \hat{x}_{F}$ where $\iota$ is defined in (49), and set $A_{m} \approx (Df^{m}(\hat{x}_{F}))^{-1}$. We start by noting that $(f(\hat{x}))_{k} = 0$ for $k\notin \mathcal {I}_{2m}$, since g(u) is quadratic. Using this and the fact that $T(\hat{x})-\hat{x} = Af(\hat{x})$ we set $y_{k}^j = (|(A_mf^{m}(\hat{x}))_{k}^j|)$ for $k\in \mathcal {I}_{m}$, $y_{k}^j = \frac{1}{k_1|\lambda _1|+k_2|\lambda _2|}((|f^{2m}(\hat{x}))_{k}^j|)$ for $k\in \mathcal {I}_{2m}\setminus \mathcal {I}_m$ and $y_{k} = 0\in \mathbb {R}^{3}$ for $k\notin \mathcal {I}_{2m}$. The bounds $Y^j$ $(j = 1,2,3)$ are then obtained by computing the finite sums $\Vert y^{j}\Vert _{\nu }$.

To derive the bounds $Z^{j}(r)$ defined in (55) we use the splitting (53). Let $v,w\in B_{1}(0)$. We start by deriving an expansion

$$\begin{aligned} (Df(\hat{x}+rv)rw- A^{\dag }rw)_{k} = z_{k,1}r + z_{k,2}r^{2}\qquad \text {with } z_{k,1},z_{k,2}\in \mathbb {R}^3. \end{aligned}$$

(61)

The explicit expressions for z are listed in Table 1.

Table 1 Expansion coefficients for $(Df(\bar{x}+rv)rw- A^{\dag }rw)_{k}$ in (61)

Our next goal is to compute a bound

$$\begin{aligned} |(DT(\hat{x}+rv)rw)_{k}^j|\le Z^j_{k,1}r + Z^j_{k,2}r^2. \end{aligned}$$

(62)

The first term to estimate is $(\text {Id }-AA^{\dag })w$. We introduce the notation $A^{\dag }_m \mathop {=}\limits ^{\text{ def }}Df^m(\widehat{x}_F)$, and by using $|w^{j}_k|\le \frac{1}{\nu ^k}$ we compute, by a direct computation, $\epsilon _{k}\in \mathbb {R}^{3}$, $k\in {\mathcal {I}}_m$ such that

$$\begin{aligned} |((\text {Id }-AA^{\dag })w)_{k}^j| \le (|\text {Id }-A_mA^{\dag }_m| \, |w_F|)_k^j \le \epsilon _{k}^j \qquad \text {for all }k\in {\mathcal {I}}_m, \end{aligned}$$

(63)

where absolute values are to be understood component-wise. Furthermore, for the tail terms we have $((\text {Id }-AA^{\dag })w)_{k} =0\in \mathbb {R}^{3}$ for $k\notin {\mathcal {I}}_m$ by construction. To accommodate matrix multiplication we collect all estimates of $z_{k,2}$ for $k\in \mathcal {I}_m$ in a vector. Namely, we define the vector $\chi _{2} \in \mathbb {R}^{3n_m}$ with $n_m = (m_1+1)(m_2+1)$ such that

$$\begin{aligned} |z_{k,2}^j|\le \chi ^{3(k_2(m_1+1)+k_1)+j}_2 \qquad \text {for } 0\le k_1 \le m_1, 0\le k_2 \le m_2, \quad j = 1,2,3. \end{aligned}$$

(64)

To be explicit, we use the estimate

$$\begin{aligned} \chi ^{3(k_2(m_1+1)+k_1)+1}_2 = 0,\quad \chi ^{3(k_2(m_1+1)+k_1)+2}_2 =\frac{2}{\nu ^k},\quad \chi ^{3(k_2(m_1+1)+k_1)+3}_2 = \frac{2}{\nu ^k}. \end{aligned}$$

Then applying the definition of A given in (51), and interpreting $A_m$ as an $3n_m \times 3n_m$ matrix, yields the values for $Z_{k,1}$ and $Z_{k,2}$ summarized in Table 2.

Table 2 Expansion coefficients for $Z_{k}(r) = Z_{k,1}r + Z_{k,2}r^2$

Finally, by estimating the finite part ($k\in {\mathcal {I}}_m$) and the tail part ($k \notin {\mathcal {I}}_m$) separately, we can compute $Z^j(r) = Z_{1}^j r+Z_{2}^j r^{2}$ by

$$\begin{aligned} Z_{1}= & {} \displaystyle \sum _{k\in \mathcal {I}_{m}}\epsilon _{k}\nu ^{k} + \frac{1}{\min \bigl \{(m_1+1)|\lambda _1|,(m_2+1)|\lambda _2|\bigr \}} \begin{pmatrix} 2|\sigma |\\ |\rho |+1+\Vert \hat{a}^1\Vert _{\nu }+\Vert \hat{a}^{3}\Vert _{\nu }\\ |\beta | + \Vert \hat{a}^1\Vert _{\nu }+\Vert \hat{a}^{2}\Vert _{\nu } \end{pmatrix} \end{aligned}$$

(65a)

$$\begin{aligned} Z_{2}= & {} \displaystyle \sum _{k\in \mathcal {I}_{m}}(|A_m| \chi _{2})_{k}\nu ^{k} + \frac{1}{\min \bigl \{(m_1+1)|\lambda _1|,(m_2+1)|\lambda _2|\bigr \}} \begin{pmatrix} 0\\ 2\\ 2 \end{pmatrix}, \end{aligned}$$

(65b)

where we have used the Banach algebra convolution estimate in $W^{\nu }$ to bound the tail sums. This completes the ingredients for (56b).

The main influence of $\nu$ on these estimates is via the terms $\Vert \hat{a}^{i}\Vert _{\nu }$ $(i = 1,2,3)$. On the other hand these norms are also controlled by the length of the stable eigenvectors $\xi _{1,2}$ appearing in definition (39), and also, albeit weakly, by $m = (m_1,m_2)$. Let us analyze this interplay.

Choice of m and $\Vert \xi _{1,2}\Vert$ The considerations that lead to the settings of the computational parameters depend on the goals in the application at hand. One might, for example, be interested in uniformly maximizing the image in phase space of the parametrization, or one might want to capture a particular point in phase space in the image, i.e., maximize the image in a certain direction. In the following we collect several observations for either task. Let us begin with a fundamental restriction; namely, the components $Z^{j}_1$ in (65) need to be smaller than one. This can be used as a first feasibility check for the validation.

Fig. 2

Top change of the validation radii while rescaling the eigenvectors (left $m=(5,5)$, right $m=(15,15)$) We see that for a larger number of modes we obtain smaller error bounds. Note in addition that the larger the norm of $\xi _{1,2}$ is the bigger the uniform error bound r on $\mathbb {B}_{\nu }$ gets. Bottom dependence of the norm of the approximate solution on the number of rescalings, hence on the norms $\Vert \xi _{1,2}\Vert$. These are an indicator for the size of the image in phase space

This motivates the following procedure (recall that we have fixed $\nu =(1,1)$, see Remark 5.1):

• 1. Choose an order $m = (m_1,m_2)$. Compute $\hat{a}$ with $\Vert \xi _{1,2}\Vert = 1.$

• 2. Attempt to check the conditions of Lemma 4.6 using the formulas derived for (54) and (56b).

• 3.

  • In case of failure rescale $\xi _{1,2} = \mu _{1,2}\xi _{1,2}$ and $\hat{a} = \mu \hat{a}$ with $0<\mu _i< 1$ $(i = 1,2)$ and repeat the second step.

  • In case of success rescale $\xi _{1,2} = \mu _{1,2}\xi _{1,2}$ and $\hat{a} = \mu \hat{a}$ with $\mu _i>0$ $(i = 1,2)$ chosen according to the maximization objective and repeat the second step until stop at failure.

In this procedure there remain two open choices, namely of $m = (m_1,m_2)$ and $\mu = (\mu _1,\mu _2)$. Let us review two options. More thorough discussion of the choice of scalings, including algorithms and implementations, can be found in Breden et al. (2015).

• 1. $m_1 = m_2$ and $\mu _1 = \mu _2>1$: uniformly maximizing the image

  We consider the two cases $m = (5,5)$ and $m = (15,15)$, see Fig. 2. First, for $m = (5,5)$, the validation succeeds with $\Vert \xi _{1,2}\Vert = 1$ with a radius of $r \approx 10^{-7}$. Recall that by Remark 4.2 the validation radius r can be seen as an accuracy measure. We thus consider smaller radius r as higher accuracy. After conducting 5 rescalings with factors $\mu _1 = \mu _2 = \frac{7}{6}$ to uniformly maximize the image, we fail to validate. The accuracy r we obtain after 4 rescalings decreased to $10^{-5}$ (for fixed m the (uniform estimate on the) accuracy naturally decreases when increasing the domain). Second, for $m = (15,15)$ we also succeed to validate for $\Vert \xi _{1,2}\Vert = 1$ but with smaller uniform error bound $r \approx 10^{-15}$. We are able to rescale 15 times with the same factors. This increases $\Vert \xi _{1,2}\Vert$ to 10.09 and increases the validation radius to $10^{-2}$.

• 2. Fast-slow choice of m and $\mu$: maximizing the image in the slow direction

  Next we consider the cases $m_1\ne m_2$ and/or $\mu _1\ne \mu _2$, see Fig. 3. We recall that $|\lambda _{1}|\approx 10|\lambda _2|$, hence we refer to $\lambda _{1/2}$ as the fast/slow eigenvalue. For most orbits the dynamics close to the origin is dominated by the slow direction. This is, for example, of interest when computing connecting orbits that approach the equilibrium along the slow direction. Capturing a large portion of the slow direction can thus be desirable. We choose $m_2 \ge m_1$ and $\mu _2>1>\mu _1$. First we choose $m_1 = m_2 = 15$ . We succeed to validate for $\Vert \xi _{1,2}\Vert = 1$ with a radius $r\approx 10^{-15}$. Let $\mu _1 = \frac{6}{7}$ and $\mu _2 = \frac{7}{6}$. We obtain 14 successful rescalings with gradually decreasing accuracy ($r \approx 10^{-3}$ after 14 rescalings). If we choose $m_1 = 5$ and $m_2 = 15$ we observe qualitatively different behavior of the validation radii.

  Starting with a success at $\Vert \xi _{1,2}\Vert = 1$ and radius $r\approx 10^{-8}$ the accuracy increases to $10^{-11}$ in the first 8 rescalings with the factors $\mu _1 = \frac{6}{7}$ and $\mu _2 = \frac{7}{6}$ until the norms of $\Vert \xi _{1,2}\Vert$ “align” with the choice of m. Then the accuracy decreases to $10^{-3}$ after 18 rescalings.

Fig. 3

Top left change of validation radii while rescaling with factor $\mu = (\frac{6}{7},\frac{7}{6})$ for the choice $m_1 = m_2 = 15$. We observe qualitatively similar behavior to the uniform scaling. Top right change of validation radii while rescaling with factor $\mu = (\frac{6}{7},\frac{7}{6})$ for the choice $m_1 = 5, m_2 = 15$. We observe qualitatively different behavior to the uniform scaling. The maximal accuracy is obtained for $\frac{\Vert \xi _2\Vert }{\Vert \xi _1\Vert }\approx 11.8$. Bottom dependence of the norm of the approximate solution on the number of rescalings, hence on the norms $\Vert \xi _{1,2}\Vert$. Note the clear dominance of the $\Vert \hat{a}^3\Vert _{\nu }$ which reflects the fact that $\xi _2 = (0,0,1)^{T}$

The above considerations can serve as a starting point for more elaborate future investigations. One might, for example, devise an optimization scheme in which one takes not only the radius r as an unknown in the radii polynomials but also considers $\nu$ or $\Vert \xi _{1,2}\Vert$, respectively, as variables.

5.1.2 Analysis for the Local Lorenz Manifold: Double Eigenvalues

In order to analyze the situation for double eigenvalues as discussed in Sect. 2.3, we choose for the parameters in the Lorenz system (59) the relation $\rho =1+(\sigma +1)^2/(4\sigma )$, leading to double eigenvalues $\lambda =-(\sigma +1)/2$. Using this data we set up the operator $f^{\text {double}}$ specified in (40). Note that the (generalized) eigenvectors $\xi _{1,2}$ fulfilling (23) can be computed explicitly in this model case. For the general case we refer to methods developed in Alefeld and Spreuer (1986) and Rump (2001). It will be subject of future work to discuss their applicability in the current context. Let us now discuss the influence of the choice of parameters m and $\nu$ (or $\Vert \xi _{1,2}\Vert$) we first define the radii polynomials as we did in 5.1.1.

To compute the bounds $Y^j$ $(j = 1,2,3)$ defined in (54) and $Z^j$ $(j = 1,2,3)$ defined in (55) we follow the same strategy as in Sect. 5.1.1. First the derivation of the Y-bounds is exactly analogous. In deriving $z_{k,i}(r)$, $i=1,2$ fulfilling in the analogue of (61) we notice that the only difference from the formulas in Table 1 is induced by the additional linear term $(k_1+1)a_{\overline{k}}$, with $\overline{k}\mathop {=}\limits ^{\text{ def }}(k_1+1,k_2-1)$ in $f^{\text {double}}$ for $|k|\ge 2$ and $k_2>0$. For $k_2=0$ one should read $a_{\overline{k}}\equiv 0$. The resulting differences in $z_{k,1}$ can be read off in Table 3.

Table 3 Expansion coefficients for $(Df(\hat{x}+rv)rw- A^{\dag }rw)_{k}$ for the double eigenvalue case, using the standard Kronecker $\delta$ symbol

To obtain $Z_{k}(r)$ fulfilling the equivalent of (62) we obtain, in addition to $\epsilon _{k}$ from (63) and $\chi _{2}$ from (64), a vector $\chi _{1}\in {\mathbb {R}}^{3n_m}$ such that

$$\begin{aligned} |z_{k,1}^{j}| \le \chi _{1}^{3(k_2(m_1+1)+k_1)+j}\qquad j = 1,2,3. \end{aligned}$$

To be precise, we set $\chi _1^{3(k_2(m_1+1)+m_1)+j} = (m_1+1)\nu _1^{-(m_1+1)}\nu _{2}^{-(k_2-1)}$ for all $1 \le k_2 \le m_2$ and $j=1,2,3$, whereas all other components of $\chi _1$ vanish. To obtain the analogue of $Z_1$ in (65) we need to bound the sum

$$\begin{aligned} \displaystyle \sum _{k\notin {\mathcal {I}}_m}\frac{k_1+1}{|\lambda _1|(k_1+k_2)}|w_{\overline{k}}^j|\nu _1^{k_1}\nu _2^{k_2} = \frac{\nu _2}{\nu _1}\displaystyle \sum _{k\notin {\mathcal {I}}_m} \frac{k_1+1}{|\lambda _1|(k_1+k_2)}|w_{\overline{k}}^j|\nu _1^{k_1+1}\nu _2^{k_2-1}. \end{aligned}$$

The following lemma can be used to control the factor $\frac{k_1+1}{|\lambda _1|(k_1+k_2)}$ uniformly for $k\notin {\mathcal {I}}_m$. We formulate it in this more general form as it will be reused for more general terms of this type in analyzing resonant eigenvalues in Sect. 5.2.

Lemma 5.1

Let $m\in \mathbb {N}^{d}$ with $m_{\tilde{\imath }} \ge 1$ for an $\tilde{\imath }\in \{1,\ldots ,d\}$. Let

$$\begin{aligned} Q_{\tilde{\imath }}\mathop {=}\limits ^{\text{ def }}\min \{ |\lambda _i|(m_i+1) : i \ne \tilde{\imath }\}. \end{aligned}$$

Then we have, with $\mathcal {I}_{m} = \{ k \in \mathbb {N}^d : k \preceq m \}$,

$$\begin{aligned} \max _{k\in \mathbb {N}^d\setminus \mathcal {I}_{m}} \frac{k_{\tilde{\imath }}+1}{|\lambda _1|k_1+\ldots +|\lambda _d|k_d} \le \max \left\{ \frac{m_{\tilde{\imath }}+2}{|\lambda _{\tilde{\imath }}| (m_{\tilde{\imath }}+1) } \,,\, \frac{m_{\tilde{\imath }}+1}{Q_{\tilde{\imath }}+|\lambda _{\tilde{\imath }}| m_{\tilde{\imath }}} \,,\, \frac{1}{Q_{\tilde{\imath }}} \right\} . \end{aligned}$$

(66)

Proof 5.1

For any $k \in \mathcal {I}_m$ there is at least one $j \in \{1,\ldots ,d\}$ such that $k_j \ge m_j+1$. We distinguish two cases:

• $k_{\tilde{\imath }}\ge m_{\tilde{\imath }}+1$. Then

  $$\begin{aligned} \frac{k_{\tilde{\imath }}+1}{|\lambda _1|k_1+\ldots +|\lambda _d|k_d} \le \frac{k_{\tilde{\imath }}+1}{|\lambda _{\tilde{\imath }}| k_{\tilde{\imath }} } \le \frac{m_{\tilde{\imath }}+2}{|\lambda _{\tilde{\imath }}| (m_{\tilde{\imath }}+1)}. \end{aligned}$$

• $0\le k_{\tilde{\imath }}\le m_{\tilde{\imath }}$. We estimate

  $$\begin{aligned} \frac{k_{\tilde{\imath }}+1}{|\lambda _1|k_1+\ldots +|\lambda _d|k_d} \le \frac{k_{\tilde{\imath }}+1}{Q_{\tilde{\imath }}+|\lambda _{\tilde{\imath }}| k_{\tilde{\imath }}} \le \max \left\{ \frac{m_{\tilde{\imath }}+1}{Q_{\tilde{\imath }}+|\lambda _{\tilde{\imath }}| m_{\tilde{\imath }}}, \frac{1}{Q_{\tilde{\imath }}} \right\} . \end{aligned}$$

The proof follows from combining these estimates. $\square$

Following the same steps as in Sect. 5.1.1 we obtain $Z_{k,1}$ as given in Table 4, while $Z_{k,2}$ remain unaltered from Table 2.

Table 4 Expansion coefficients for $Z_{k}(r) = Z_{k,1}r + Z_{k,2}r^2$

Hence, one finds (in all the cases discussed below) that $Z_1$ is given by

$$\begin{aligned} Z_{1}= & {} \displaystyle \sum _{k\in \mathcal {I}_{m}}Z_{k,1}\nu ^{k} + \frac{1}{|\lambda _1|\min \{m_1+1,m_2+1\}}\begin{pmatrix} 2|\sigma |\\ |\rho |+1+\Vert \hat{a}^1\Vert _{\nu }+\Vert \hat{a}^{3}\Vert _{\nu }\\ |\beta | + \Vert \hat{a}^1\Vert _{\nu }+\Vert \hat{a}^{2}\Vert _{\nu } \end{pmatrix} \\&+ \frac{\nu _2}{\nu _1}\frac{m_1+2}{|\lambda _1|(m_1+1)}. \end{aligned}$$

Recalling the necessary condition $Z_1^j\le 1$ from above, we point out that the term $\frac{\nu _2}{\nu _1}\frac{m_1+2}{|\lambda _1|(m_1+1)}$ is crucial. In particular, we certainly need $\frac{\nu _2}{\nu _1 |\lambda _1|} <1$. Therefore, in our analysis of the computational parameters we fix $\Vert \xi _{1,2}\Vert$ and vary $\nu _{1,2}$.

Remark 5.2

The condition from Lemma 2.7 reads $\ell _0\bigl (\hat{\nu }_{1},\frac{\hat{\nu }_{2}}{|\lambda _1|}\bigr ) \le \nu _{1}$. However, the necessary condition $\frac{\nu _2}{\nu _1 |\lambda _1|} <1$ implies that $\ell _0\bigl (\nu _{1},\frac{\nu _{2}}{|\lambda _1|}\bigr ) = \nu _1$, hence in practice one simply takes $\hat{\nu }= \nu$.

Let us now consider different choices of parameters $\beta ,\rho ,\sigma$. We fix $\beta = \frac{8}{3}$ and consider $\sigma = -3,-5,-11,-21$ with $\rho = \frac{4}{3},\frac{9}{5},\frac{36}{11},\frac{121}{21}$. This corresponds to double eigenvalues $\lambda _1 = 1,2,5,10$. Thus we compute 2D unstable manifolds (simply replacing g by $-g$ everywhere in the analysis). Note that this does not necessitate an adaptation of the formulas for the radii polynomials. Table 5 offers a comparison of the validation success in terms of the decay rate $\nu$.

Table 5 For fixed $m = (7,6)$ and $\Vert \xi _{1,2}\Vert = \frac{1}{50}$, we give the corresponding validation radii (if there was one; failure is denoted by $-$) on the different domain sizes corresponding to the different decay rates $\nu$

Thus we see that the bigger we choose the magnitude of the eigenvalue, the bigger is the domain of convergence of the parametrization that we are able to validate. Moreover, the smaller the eigenvalue, the bigger the ratio $\nu _1/\nu _2$ needs to be. This reflects the crucial role of the term $\frac{\nu _2}{\nu _1}\frac{m_1+2}{|\lambda _1|(m_1+1)}$.

5.2 Coexistence of Hexagonal and Trivial Patterns

As an example of an application to a case with regular resonant eigenvalues, we turn our attention to the existence of solutions of (2) exhibiting certain patterns. The asymptotic analysis in Doelman et al. (2003) reduces the problem of finding transition layers between stationary patterns of (2) to connecting orbit problems for the system of ODEs (1). We proceed to analyze (1) along the same lines as in van den Berg et al. (2015). To this end we set $u_1 = u, u_2 = u^{\prime }, u_3 = v$ and $u_4 = v^{\prime }$ in (1) and rewrite it as

$$\begin{aligned} {u}^{\prime } = g(u) = \begin{pmatrix} u_2\\ -\frac{\gamma }{4}u_1-\frac{\sqrt{2}}{4}u_3^{2} + \frac{3}{8}u_1^{3}+3u_1u_3^{2}\\ u_4\\ -\gamma u_3 -\frac{\sqrt{2}}{2} u_1u_3 +9u_3^{3} + 3u_1^{2}u_3 \end{pmatrix} \end{aligned}$$

(67)

with $u = (u_1,u_2,u_3,u_4)^{T}$. The relation between the parameters $\gamma ,\mu$ and $\beta$ is given by $\gamma = \frac{\mu }{\beta ^2}$. We refer to Doelman et al. (2003) for a complete description of the seminal asymptotic reduction of the PDE (2) to the ODE system (67), obtained via a combination of spatial dynamics, bifurcation theory and geometric singular perturbation theory. For further details about the particular form (67) one may consult (van den Berg et al. 2015). We take the same viewpoint as in van den Berg et al. (2015) and investigate by rigorous numerical techniques, for fixed parameter value $\gamma$, connecting orbits between equilibria of (67). While in van den Berg et al. (2015) the configuration for the coexistence of hexagons and rolls (spots and stripes) is considered, we concern ourselves with the coexistence of the trivial state and hexagonal patterns. In terms of (67) this corresponds to a connecting orbit between the two fixed points $p_1 = (\sqrt{2}u_3^{*},0,u_3^{*},0)^T$, where $u_3^{*} = \frac{1+\sqrt{1+60\gamma }}{30}$, and $p_2 = (0,0,0,0)^T$. As (67) is Hamiltonian, a necessary condition for the connection between $p_1$ and $p_2$ to exist is for the equilibria to lie on the same energy level, which is the case for $\gamma = -\frac{2}{135}$.

The equilibrium $p_2$ has resonant eigenvalues ($\lambda _1=2\lambda _2$). For this reason the case of coexistence of the trivial state and the hexagonal spot pattern was not considered in van den Berg et al. (2015). However, our current approach to validating the (un)stable manifold is well suited for this situation.

To compute the connecting orbit we adapt the approach of van den Berg et al. (2015). Introducing a rescaling factor $L>0$ we aim at solving

$$\begin{aligned} \left\{ \begin{array}{rl} u^{\prime }(t) &{}= Lg(u(t)) \qquad t\in [0,1]\\ u(0) &{}\in W^{u}_{\text {loc}}(p_1)\\ u(1) &{}\in W^{s}_{\text {loc}}(p_2) \end{array}\right. \end{aligned}$$

(68)

with $u(t) = (u_1(t),u_2(t),u_3(t),u_4(t))$. The main aim of the current paper is to construct efficient rigorously validated descriptions of the local (un)stable manifolds. As explained in detail in van den Berg et al. (2015), once we have such parametrizations $P^{u}: \mathbb {R}^{2}\supset \mathbb {B}_{1}^{{sym }}\rightarrow \mathbb {R}^{4}$ of the local unstable manifold of $p_1$ and $P^{s}: \mathbb {R}^{2}\supset \mathbb {B}_{1}^{{sym }}\rightarrow \mathbb {R}^{4}$ of the local stable manifold of $p_2$, (68) can be solved by finding a zero of the operator

$$\begin{aligned} F(\psi ,\phi ,u)(t) = \begin{pmatrix} u_{1}(1) - P^{s}_1(\theta (\psi ))\\ u_{3}(1) - P^{s}_3(\theta (\psi ))\\ u_{4}(1) - P^{s}_4(\theta (\psi ))\\ u(t) - P^{u}(\phi ) - \displaystyle \int _{0}^{t}Lg(u(s))ds \end{pmatrix}, \end{aligned}$$

(69)

where $\theta (\psi ) \mathop {=}\limits ^{\text{ def }}(\rho \cos (\psi ),\rho \sin (\psi ))$ with some fixed $\rho < 1$ (playing the role of the phase condition in this otherwise autonomous problem). The fact that the second component $u_{2}(1) - P^{s}_2(\theta (\psi ))=0$ can be replaced by the a posteriori check of

$$\begin{aligned} \text {sign}(u_{2}(1)) = \text {sign}(P^{s}_{2}(\theta (\psi ))) \end{aligned}$$

is explained in Lemma 2 in van den Berg et al. (2015) and is related to the Hamiltonian nature of the problem. Using the phase condition (i.e., fixing $\rho$) and omitting the second component deals on the one hand with the fact that every time shift of a connecting orbit is again a connecting orbit and on the other hand with the fact that the intersection of the two-dimensional unstable and stable manifolds corresponding to the connecting orbit is not transverse in $\mathbb {R}^4$. In a nutshell, they guarantee the isolation of the zero of F that we set out to find.

To rigorously compute zeros of (69) we choose to discretize the time dependence using a Chebyshev series (other choices, such as splines, are also possible). For details on how this is done in this example we refer the reader to van den Berg et al. (2015) and for the general method to Lessard and Reinhardt (2014). In this paper we focus on the rigorous computation of the maps $P^{s,u}$ and especially $P^{s}$, as there we encounter eigenvalue resonances. The validated computation of $P^{u}$ is conducted analogously to the Lorenz equation explained above and we do not give any further details below. Furthermore, in order to validate zeros of (69) we need rigorous information on $\Vert DP^{s,u}(\theta )\Vert$ that we obtain in the same way as explained in Remark 3 in van den Berg et al. (2015). Note that by Remark 4.2 the a posteriori bound $\delta _{s,u}$ corresponds to our validation radius r.

We now delve into the validated computation of the stable manifold of the origin, which has resonant eigenvalues. Explicitly, the eigenvalues of $Dg(p_2)$ with negative real part are given by $\lambda _1 = -\sqrt{-\gamma }$ and $\lambda _2 = -\frac{\sqrt{-\gamma }}{2}$ with corresponding eigenvectors $\xi _1 = (0,0,-\frac{1}{\sqrt{-\gamma }},1)^T$ and $\xi _{2} = (-\frac{2}{\sqrt{-\gamma }},1,0,0)^T$. We note that $2\lambda _2 = \lambda _1$, so condition (5) holds with $\tilde{\imath }= 1$ and $\tilde{k} = (0,2)$.

Following the approach described in Sect. 2.4 we choose the nonlinear normal form

$$\begin{aligned} h^{s}(\theta ) = \begin{pmatrix} 2 \lambda _2 \theta _1 + \tau \theta _2^2\\ \lambda _2 \theta _2 \end{pmatrix} \end{aligned}$$

(70)

to describe the dynamics in the (stable) parameter space. The coefficients $c_k = c_k(a;\gamma )$ in (41) are given by

$$\begin{aligned} c_k = \begin{pmatrix} a_{k}^{2}\\ -\frac{\gamma }{4}a_k^1-\frac{\sqrt{2}}{4}(a^3*a^3)_k + \frac{3}{8}(a^1*a^1 *a^1)_k+3(a^1*a^3*a^3)_k\\ a_k^4\\ -\gamma a_k^3 -\frac{\sqrt{2}}{2} (a^1*a^3)_k +9(a^3 *a^3 *a^3)_k + 3(a^1 *a^1 *a^3)_k \end{pmatrix}. \end{aligned}$$

This completes the ingredients for (41) in the particular case of (67). Note that the condition in Lemma 2.7c) reads $\ell _0\bigl (\theta _{1},\frac{\tau \theta _2^{2}}{|\lambda _{1}|}\bigr ) \le \nu _{1}$, which we easily check explicitly.

Derivation of the bounds To define the radii polynomials specified in (56b) we first need to compute the bounds Y and Z defined in (54) and (55). Let $f = f^{\text {regres}}$ as specified in (41) where $\zeta = \frac{1}{\sqrt{1-\gamma }} (0,0,-\sqrt{-\gamma },1)^T \in \ker (A^T)$, with A defined in (29). Finally, let an approximate solution $\hat{x} = \iota \hat{x}_{F}$ with $f^m(\hat{x}_{F})\approx 0$ be given, and let $A_m \approx (Df^{m}(\hat{x}_{F}))^{-1}$. Concerning the bounds Y we (again) note that $f(\hat{x})_{k} = 0$ for $k\notin \mathcal {I}_{3m}$, since g is a cubic nonlinearity. Therefore the construction of Y fulfilling (54) is analogous to the Lorenz case in Sect. 5.1. Again as in Sect. 5.1, to obtain $Z^j(r) = Z^j_{1}r+Z^j_{2}r^2 + Z^j_3 r^3$ in (55) we first compute $z_{k}(r) = z_{k,1}r+z_{k,2}r^2+z_{k,3}r^3$ fulfilling the analogue of (61). The result is summarized in Table 6 in “Appendix 1.” Note that $z_{-1}(r) = 0$, as $f_{-1}$ is linear in $a_{\tilde{k}}$ and $\tilde{k}\preceq m$ for our choice of m.

The main deviation from the non-resonant case is given by the off-diagonal linear terms introduced by the resonance. Note that this is analogous to the double eigenvalue case, but with the additional difference given by the presence of the additional unknown $\tau$. To expand the bounds

$$\begin{aligned}&|(DT(\hat{x}+rv)rw)_k^j| \le Z^j_{k,1}r + Z^j_{k,2}r^2 + Z^j_{k,3} r^3 \\&\quad \text {for } k \in {\mathcal {I}}_m= \{0\} \sqcup \{k\in \mathbb {N}^2 : k \preceq m\}, \end{aligned}$$

we first find bounds $\epsilon _k$ for $k \in \mathcal {I}_{m}$ such that

$$\begin{aligned} |((\text {Id }-AA^{\dag })w)_{k}^j| \le \epsilon _{k}^j \qquad j = 1,2,3,4. \end{aligned}$$

(71)

Note that $((\text {Id }-AA^{\dag })w)_{k} = 0\in \mathbb {R}^{4}$ for $k\notin \mathcal {I}_{m}$ by construction. Furthermore we construct, for $i = 1,2,3$, the vector $\chi _{i} \in \mathbb {R}^{4n_m+1}$ with $n_m = (m_1+1)(m_2+1)$ such that

$$\begin{aligned} |z_{k,i}^j|\le \chi _i^{1+4(k_2(m_1+1)+k_1)+j} \qquad j = 1,2,3,4. \end{aligned}$$

(72)

Note that $\chi _{i}^{1} = 0$ for $i = 1,2,3$, since $f_{-1}$ is linear. Then, applying the definition of A given in (51) yields the values for $Z_{k,1}$, $Z_{k,2}$ and $Z_{k,3}$ summarized in Table 7 in “Appendix 1.” Summing up $Z_{k,i}$ component-wise while splitting into a finite part and infinite tail yields Z(r). The result is shown in Table 8 in “Appendix 1.” An important ingredient in computing $Z_1$ is the control of terms of the form

$$\begin{aligned} \begin{aligned}&\hat{\tau }\displaystyle \sum _{k\notin \mathcal {I}_{m}}\frac{k_{\tilde{\imath }}}{|\lambda _1|k_1 + |\lambda _2|k_2}|w_{\underline{k}}|\nu _1^{k_1}\nu _2^{k_2}, \qquad \text {where } \underline{k}\mathop {=}\limits ^{\text{ def }}(k_1+1,k_2-2). \end{aligned} \end{aligned}$$

(73)

We use Lemma 5.1 to bound the factor $\frac{k_{\tilde{\imath }}}{2|\lambda _2|k_1 + |\lambda _2|k_2}$ uniformly for $k\notin {\mathcal {I}}_m$. In the specific problem under consideration we are in luck, since $\hat{\tau } \approx 0$, hence the contribution from the term (73) is small. This stems from the fact that the exact solution is $\tau = 0$ as we derive analytically in “Appendix 2.”

However, the strength of our method is that one does not need to determine the coefficients of the normal form beforehand, as they are part of the overall set of unknowns for the nonlinear problem.

Numerical implementation The implementation of the validation of an approximate zero of (69) can be found at the webpage Code page (2015). There, a complete instruction on how to run the codes can be found.

We list the main parameters for the computations, which were chosen after numerical experimentation. As time rescaling parameter we choose $L = 43.2034$ in (68). For both the stable and unstable manifold we choose as domain radius in (6) $\nu = (1,1)$.

• Parametrization order: unstable $m = (15,15)$, stable $m = (15,15)$.

• Scaling of eigenvectors: unstable $\Vert \xi _1\Vert _2 = 0.005$, $\Vert \xi _2\Vert _2 = 0.02$ stable $\Vert \xi _1\Vert _2 = 0.0085$, $\Vert \xi _2\Vert _2 = 0.0214$

The Y-bounds are explained above and the Z-bounds which we use to define the radii polynomials from (56) are summarized in Table 8. Using them to check the conditions of Lemma 4.6 we obtain the following validation radii:

$$\begin{aligned} \begin{aligned} \text {unstable manifold:}\quad r = 1.0823\times 10^{-12}, \\ \text {stable manifold:} \quad r = 5.2217\times 10^{-12}. \end{aligned} \end{aligned}$$

Fig. 4

Profiles of the u and v component of the rigorously verified connecting orbit. The blue part of either orbit is computed using Chebyshev series with the implementation from van den Berg and Sheombarsing (2015) and the red and green parts are computed using the conjugation maps $P^{u,s}$ harnessing the formula $u(t)=P(\Psi ^{u,s}(t,\theta ))$ with $\Psi ^{u,s}(t,\theta )$ the flow induced by $h^{u,s}$ for $\theta \in \hat{\mathbb {B}}_{(1,1)}^{{sym }}$ (see Lemma 2.6). One time unit corresponds to $L = 43.2034$

For the validation of the connection we use the approach of van den Berg et al. (2015) in conjunction with the implementation of van den Berg and Sheombarsing (2015). The validated solution profiles are shown in Fig. 4.

Appendices

Appendix 1: Formulas for the Expansion Coefficients $z_k$ and $Z_k$ for (67)

Let $f = f^{\text {regres}}$ defined in (41) be initiated according to the resonance present in the stable manifold of the origin in $\mathbb {R}^4$ as a fixed point of (67). That is $\tilde{k} = (0,2)$ and $\tilde{\imath }= 1$ in (41). Let $\hat{x} = (\hat{\tau },\hat{a}) = (\hat{\tau },\hat{a}^1,\hat{a}^2,\hat{a}^3,\hat{a}^4)$. To make the expansion

$$\begin{aligned} (Df(\hat{x}+rv)rw-A^{\dag }rw)_k = z_{k,1}r + z_{k,2}r^2 + z_{k,3}r^{3} \end{aligned}$$

explicit, we first define the operations

$$\begin{aligned} H_{ij}(a) = a^{i}*a^{j} \qquad \text {and}\qquad H_{ijl}(a) = a^{i}*a^{j}*a^{l}. \end{aligned}$$

Denote $v = (\tau _v,v_a)$ and $v = (\tau _w,w_a)$. By a direct calculation one derives expansions of the form

$$\begin{aligned} \begin{aligned} H_{ij}(\hat{a}+rv_a)rw&= \eta _{ij,1}r + \eta _{ij,2}r^{2}\\ H_{ijl}(\hat{a}+rv_a)rw&= \eta _{ijl,1}r + \eta _{ijl,2}r^2 + \eta _{ijl,3}r^{3}, \end{aligned} \end{aligned}$$

where, for example, $\eta _{ij,2}=v_a^{i}*w_a^{j} + v_a^{j}*w_a^{i}$.

Table 6 Expansion coefficients for $(Df(\hat{x}+rv)rw- A^{\dag }rw)_{k}$

Recall that the special case $k = -1$ yields $(Df(\hat{x}+rv)rw-A^{\dag }rw)_{-1} = 0$. The result for the remaining k is given in Table 6, where we use the notation $\underline{k}=(k_1+1,k_2-2)$, and whenever $k_2<2$ one should read 0 for terms involving $\underline{k}$. Concerning the bounds $\chi _{i}$ defined in (72), we proceed as in Sect. 5.1. In order to define $\chi _{1}$ we use

$$\begin{aligned} |w_{\underline{k}}^j|\le \frac{1}{\nu _1^{k_1+1}\nu _2^{k_2-2}} \end{aligned}$$

to control the term (73) for $k_1=m_1$. Note that all other components of $\chi _1$ vanish. To define $\chi _{2,3}$ we note, in addition, that

$$\begin{aligned} |(\eta _{ij,2})_k^{j}|\le \frac{2}{\nu ^k}, \qquad |(\eta _{ijl,2})_k^{j}|\le \frac{2}{\nu ^k}\left( \Vert \hat{a}^{i}\Vert _{\nu }+ \Vert \hat{a}^{j}\Vert _{\nu }+\Vert \hat{a}^{l}\Vert _{\nu }\right) , \qquad |(\eta _{ijl,3})_k^{j}|\le \frac{3}{\nu ^k}. \end{aligned}$$

In Table 7 we summarize the coefficients $Z_{k,i}$ appearing in the bounds $|(DT(\hat{x}+rv)rw)_{k}^j| \le Z^j_{k,1} r + Z^j_{k,2} r^2 +Z^j_{k,3} r^3$. We are now ready to define $Z_{-1}(r) = Z_{-1,1}r$.

The explicit expression for $Z^{j}(r) = Z_{1}^jr + Z_{2}^j r^2 + Z_3^j r^{3}$, $j =1,2,3,4$ is collected in Table 8.

Table 7 Bounds for $|(DT(\hat{x}+rv)rw)_{k}^j|$

Table 8 Z-bounds

Appendix 2: Analytical Proof that $\tau = 0$.

In the following we show analytically that the additional parameter $\tau$ in (70) vanishes for the exact solution.

Imposing the linear constraints (9) we obtain

$$\begin{aligned} \begin{aligned} a_{00}&= (0,0,0,0)^{T}\quad a_{10} = (0,0,-\frac{1}{\sqrt{-\gamma }},1)^T \quad a_{01} = (-\frac{2}{\sqrt{-\gamma }},1,0,0)^T. \end{aligned} \end{aligned}$$

(74)

In order to show that $\tau = 0$ we use the formula (31). Recall that we computed $\zeta = \frac{1}{\sqrt{1-\gamma }}(0,0,-\sqrt{-\gamma },1)^T$. Considering (29) with $\tilde{\imath }= 1$ and $\tilde{k} = (0,2)$ with the equilibrium $p = (0,0,0,0)$ for g specified in (67) we compute a concrete formula for $b_{02}$:

$$\begin{aligned} b_{02} = \begin{pmatrix} 0\\ -\frac{\sqrt{2}}{4}(a_{01}^{3})^2 + \frac{9}{8}a_{00}^1(a_{01}^1)^2+3\left( a_{00}^3(a_{01}^1)^2 + 2a_{01}^3a_{00}^1a_{01}^1\right) \\ 0\\ -\frac{\sqrt{2}}{2}a_{01}^1a_{01}^3 + 27a_{00}^3a_{01}^3a_{01}^3+3\left( a_{00}^1(a_{01}^3)^2 + 2a_{01}^1a_{00}^3a_{01}^3\right) \end{pmatrix}. \end{aligned}$$

Using (74) we see that $b_{02} = (0,0,0,0)$, which implies $\tau = 0$. As a result one could deal with this particular resonance in an ad-hoc fashion by prescribing in addition to (74) $a_{02}$ as any solution of $(Dg(0)-\lambda _1 I_4)a_{02} = 0$ and choosing

$$\begin{aligned} h^{s}(\theta ) = \begin{pmatrix} \lambda _1\theta _1\\ \lambda _2\theta _2 \end{pmatrix} \end{aligned}$$

just as in the non-resonant case. The one we singled out by imposing (30) is $a_{02} = (0,0,0,0)$.