Isotonic Regression via Partitioning

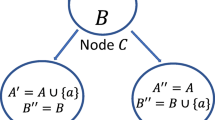
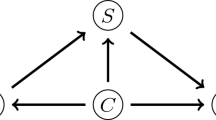
Abstract

Algorithms are given for determining weighted isotonic regressions satisfying order constraints specified via a directed acyclic graph (DAG). For the L ₁ metric a partitioning approach is used which exploits the fact that L ₁ regression values can always be chosen to be data values. Extending this approach, algorithms for binary-valued L ₁ isotonic regression are used to find L _p isotonic regressions for 1<p<∞. Algorithms are given for trees, 2-dimensional and multidimensional orderings, and arbitrary DAGs. Algorithms are also given for L _p isotonic regression with constrained data and weight values, L ₁ regression with unweighted data, and L ₁ regression for DAGs where there are multiple data values at the vertices.

Appendix: Computing the L p Mean

The computation of the L _p -mean of a level set for general p is more complicated than for p=1,2, or ∞. We are interested in identifying those aspects which might be more than linear in the time of the remainder of the algorithm. We assume that the data values have been presorted.

Simple calculus [11] shows that the L _p mean of the data (y,w) is the unique C such that

$$\sum_{y_i > C} w_i (y_i-C)^{p-1} = \sum_{y_j < C} w_j (C-y_j)^{p-1} $$

(7)

which does not, in general, have an analytic solution. An important aspect is to determine the data values that bracket the L _p mean, i.e., to determine which are in the RHS and which are on the LHS of (7).

Given the bracketing values, the time to find the mean to desired accuracy may depend upon the data and we make no assumptions concerning it. Given p, n, and data (y,w), the total time to find all L _p means used in the algorithm is decomposed into a part independent of the data and the remaining portion, denoted $\mathcal{T}_{p}(n,\mathbf{y},\mathbf{w})$, that is data dependent. For general p the data independent portion requires evaluating (7) for each set at least once per partitioning stage, and thus Θ(n) time per stage. Since there can be Θ(n) stages in each of the algorithms in Sect. 5, the data independent time for finding means is Θ(n ²) once the bracketing values are known. By first partitioning on data values, all of the partitioning algorithms can determine the bracketing values in time no more than the remaining time of the algorithm.

If p is an even integer, (7) reduces to finding the unique solution of ∑ _i=1,n w _i (y _i −C)^p−1=0, i.e., no bracketing values nor presorting are required. This is a sum of (p−1)st degree polynomials, and hence can be determined by summing up, over the data values, the coefficients of each term and then evaluating the result. For p an odd integer once again the terms are polynomials so, given the bracketing values, one can use sums of coefficients to evaluate the summations in (7). Since roots of polynomials of degree ≤4 can be found exactly in constant time, $\mathcal{T}_{2} = \mathcal{T}_{3} = \mathcal{T}_{4} =\mathcal{T}_{5} = 0$.

For PAV sets are merged rather than partitioned. This does not change the data independent time for general p, but for p an even integer each set is reduced to p+1 coefficients and merging sets merely requires adding coefficients. Hence the data independent time is Θ(n). For p odd the situation is a bit more complex since the bracketing values are needed. One can construct a balanced search tree where data values are keys and at each node, for each term there is the sum of the coefficients beneath it. The only change from being on the LHS vs. the RHS of (7) is whether the term has a plus or minus sign, and hence, given this tree, one can descend through the tree and determine the bracketing data values in logarithmic time. Merging sets corresponds to merging their trees, including maintaining the information about sums of coefficients in subtrees. With careful merging this can be accomplished in Θ(nlogn) total time.