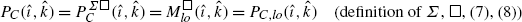Fast Distance Multiplication of Unit-Monge Matrices

Abstract

Monge matrices play a fundamental role in optimisation theory, graph and string algorithms. Distance multiplication of two Monge matrices of size n can be performed in time O(n ²). Motivated by applications to string algorithms, we introduced in previous works a subclass of Monge matrices, that we call simple unit-Monge matrices. We also gave a distance multiplication algorithm for such matrices, running in time O(n ^1.5). Landau asked whether this problem can be solved in linear time. In the current work, we give an algorithm running in time O(nlogn), thus approaching an answer to Landau’s question within a logarithmic factor. The new algorithm implies immediate improvements in running time for a number of algorithms on strings and graphs. In particular, we obtain an algorithm for finding a maximum clique in a circle graph in time O(nlog² n), and a surprisingly efficient algorithm for comparing compressed strings. We also point to potential applications in group theory, by making a connection between unit-Monge matrices and Coxeter monoids. We conclude that unit-Monge matrices are a fascinating object and a powerful tool, that deserve further study from both the mathematical and the algorithmic viewpoints.

1 Introduction

A matrix is called Monge, if its density matrix is nonnegative. Monge matrices play a fundamental role in optimisation theory, graph and string algorithms. Distance multiplication (also known as min-plus or tropical multiplication) of two Monge matrices of size n can be performed in time O(n ²). Motivated by applications to string comparison, we introduced (using different terminology) in [60, 61] the following subclass of Monge matrices. A matrix is called unit-Monge, if its density matrix is a permutation matrix; we further restrict our attention to a subclass of simple unit-Monge matrices, which satisfy a straightforward boundary condition. In [60, 61], we gave an algorithm for distance multiplication of such matrices, running in time O(n ^1.5). Landau [43] asked (again using different terminology) whether this problem can be solved in linear time. In the current work, we give an algorithm for distance multiplication of simple unit-Monge matrices, running in time O(nlogn), thus approaching an answer to Landau’s question within a logarithmic factor.

Our study of unit-Monge matrices is motivated primarily by their applications to string comparison and approximate pattern matching in strings. We presented a number of such algorithmic applications in [41, 42, 61–63, 65], and two biological applications in [7, 52]. Our new distance multiplication algorithm implies immediate improvements in running time for a number of string comparison and graph algorithms: semi-local longest common subsequences between permutations; longest increasing subsequence in a cyclic permutation; maximum clique in a circle graph; longest common subsequence between a grammar-compressed string and an uncompressed string. In the current work, we give a brief overview of these applications and the improvements brought about by faster distance multiplication of simple unit-Monge matrices.

This paper is a revised and extended version of [64]. Further details and applications can be found in [57].

2 Terminology and Notation

For indices, we will use either integers, or half-integers

$$\begin{aligned} &\{\ldots, -2, -1, 0, 1, 2, \ldots\} \\ &\biggl\{\ldots, -\frac{5}{2}, -\frac{3}{2}, -\frac{1}{2}, \frac{1}{2}, \frac{3}{2}, \frac{5}{2}, \ldots\biggr\} \end{aligned}$$

For ease of reading, half-integer variables will be indicated by hats (e.g. $\hat{\imath}$, $\hat{\jmath}$). It will be convenient to denote

for any integer or half-integer i. The set of all half-integers can now be written as

We denote integer and half-integer intervals by

$$\begin{aligned} &[i:j] = \{i, i+1, \ldots, j-1, j\} \\ &\langle i:j\rangle= \biggl\{i+\frac{1}{2}, i+\frac{3}{2}, \ldots, j- \frac{3}{2}, j-\frac{1}{2}\biggr\} \end{aligned}$$

A function of an integer argument will be called unit-monotone increasing, if for every successive pair of values, the difference between the successor and the predecessor is either 0 or 1.

We will make extensive use of matrices with integer elements, and with integer or half-integer indices.¹ Given two index ranges I, J, it will be convenient to denote their Cartesian product by (I∣J). We extend this notation to Cartesian products of intervals:

$$\begin{aligned} &[i_0:i_1 \mid j_0:j_1] = \bigl([i_0:i_1] \mid[j_0:j_1] \bigr) \\ &\langle{i_0:i_1 \mid j_0:j_1} \rangle= \bigl(\langle{i_0:i_1}\rangle\mid \langle{j_0:j_1}\rangle\bigr) \end{aligned}$$

Given index ranges I, J, a matrix over (I∣J) is indexed by i∈I, j∈J. A matrix is nonnegative, if all its elements are nonnegative.

The matrices we consider can be implicit, i.e. represented by a compact data structure that supports access to every matrix element in a specified (typically small, but not necessarily constant) time. If the query time is not given, it is assumed by default to be constant.

We will use the parenthesis notation for indexing matrices, e.g. A(i,j). We will also use a straightforward notation for selecting subvectors and submatrices: for example, given a matrix A over [0:n∣0:n], we denote by A[i ₀:i ₁∣j ₀:j ₁] the submatrix defined by the given sub-intervals. A star ∗ will indicate that for a particular index, its whole range is used, e.g. A[∗∣j ₀:j ₁]=A[0:n∣j ₀:j ₁].

We will denote by A ^T the transpose of matrix A, and by A ^R the matrix obtained from A by counterclockwise 90-degree rotation. Given a matrix A over [0:n∣0:n] or 〈0:n∣0:n〉, we have

for all i,j.

We now introduce two fundamental combinatorial operations on matrices. The first operation obtains an integer-indexed matrix from a half-integer-indexed matrix by summing up, for each of the integer points, all matrix elements that lie below and to the left of the given point.

Definition 1

Let D be a matrix over 〈i ₀:i ₁∣j ₀:j ₁〉. Its distribution matrix D ^Σ over [i ₀:i ₁∣j ₀:j ₁] is defined by

for all i∈[i ₀:i ₁], j∈[j ₀:j ₁].

The second operation obtains a half-integer-indexed matrix from an integer-indexed matrix, by taking a four-point difference around each given point.

Definition 2

Let A be a matrix over [i ₀:i ₁∣j ₀:j ₁]. Its density matrix A ^□ over 〈i ₀:i ₁∣j ₀:j ₁〉 is defined by

for all $\hat{\imath}\in\langle{i_{0}:i_{1}}\rangle$, $\hat{\jmath }\in\langle{j_{0}:j_{1}}\rangle$.

The operations of taking the distribution and the density matrix are close to be mutually inverse. For any finite matrices D, A as above, and for all i, j, we have

$$\begin{aligned} &D^{\varSigma\square} = D \\ &A^{\square\varSigma}(i,j) = A(i,j) - A(i_1,j) - A(i,j_0) + A(i_1,j_0) \end{aligned}$$

When matrix A is restricted to have all zeros on its bottom-left boundary (i.e. in the leftmost column and the bottom row), the two operations become truly mutually inverse. We introduce special terminology for such matrices.

Definition 3

Matrix A will be called simple, if A(i ₁,j)=A(i,j ₀)=0 for all i, j. Equivalently, A is simple if A ^□Σ=A.

The following class of matrices plays an important role in optimisation theory (see Burkard et al. [13] for an extensive survey), and also arises in graph and string algorithms.

Definition 4

Matrix A is called a Monge matrix, if

for all i≤i′, j≤j′. Equivalently, matrix A is a Monge matrix, if A ^□ is nonnegative.

Our techniques will rely on structures that have permutations as their basic building blocks. We will be dealing with permutations in matrix form, exploiting the symmetry between indices and elements of a permutation.

Definition 5

A permutation (respectively, subpermutation) matrix is a zero-one matrix containing exactly one (respectively, at most one) nonzero in every row and every column.

Typically, permutation and subpermutation matrices will be indexed by half-integers. An identity matrix is a permutation matrix Id over an interval range 〈i ₀:i ₁∣i ₀:i ₁〉, such that $\mathit{Id}(\hat{\imath},\hat{\jmath})=1$, iff $\hat {\imath}=\hat{\jmath}$.

When dealing with (sub)permutation matrices, we will write “nonzeros” for “index pairs corresponding to nonzeros”, as long as this does not lead to confusion.

Due to the extreme sparsity of (sub)permutation matrices, it would obviously be wasteful and inefficient to store them explicitly. Instead, we will normally assume that a permutation matrix P of size n is given implicitly by the underlying permutation and its inverse, i.e. by a pair of arrays π, π ⁻¹, such that $P(\hat{\imath},\pi(\hat{\imath})) = 1$ for all $\hat {\imath}$, and $P(\pi^{-1}(\hat{\jmath}),\hat{\jmath}) = 1$ for all $\hat {\jmath}$. This compact representation has size O(n), and allows constant-time access to each nonzero of P by its row index, as well as by its column index. The implicit representation for subpermutation matrices is analogous.

The following subclasses of Monge matrices will play a crucial role in this work.

Definition 6

Matrix A is called a unit-Monge (respectively, subunit-Monge) matrix, if A ^□ is a permutation (respectively, subpermutation) matrix.

By Definitions 4, 6, any unit-Monge matrix is subunit-Monge, and any subunit-Monge matrix is Monge (since the corresponding density matrix A ^□ is a (sub)permutation matrix, and hence nonnegative).

Our particular focus will be on square matrices A that are both simple and unit-Monge. By Definitions 3, 6, this holds if and only if A=P ^Σ, where P is a permutation matrix. Matrix P can be regarded as an implicit representation of the simple unit-Monge matrix A=P ^Σ.

Example

The following matrix is simple unit-Monge:

In our algorithms, we will need to access matrix elements via incremental queries. Given an element of an implicit simple (sub)unit-Monge matrix, such a query returns the value of a specified adjacent element.

Theorem 1

Given a permutation matrix P of size n, and the value P ^Σ(i,j), i,j∈[0:n], the values P ^Σ(i±1,j), P ^Σ(i,j±1), where they exist, can be queried in time O(1).

Proof

Straightforward from the definitions; see [57] for details. □

3 Matrix Distance Multiplication

3.1 Distance Multiplication Monoids

The (min,+)-semiring of integers is one of the fundamental structures in algorithm design. In this semiring, the operators min and +, denoted by ⊕ and ⊙, play the role of addition and multiplication, respectively. The (min,+)-semiring is often called distance (or tropical) algebra. For a detailed introduction into this and related topics, see e.g. Rote [54], Gondran and Minoux [30], Butković [14]. An application of the distance algebra to string comparison has been previously suggested by Comet [16].

Throughout this section, vectors and matrices will be indexed by integers beginning from 0, or half-integers beginning from $0^{+} = \frac{1}{2}$. All our definitions and statements can easily be generalised to indexing over arbitrary integer or half-integer intervals.

Multiplication in the (min,+)-semiring of integers can be naturally extended to integer matrices.

Definition 7

Let A, B, C be matrices over [0:n ₁∣0:n ₂], [0:n ₂∣0:n ₃], [0:n ₁∣0:n ₃] respectively. The matrix distance product A⊙B=C is defined by

for all i∈[0:n ₁], k∈[0:n ₃].

We now consider three different monoids of integer matrices with respect to matrix distance multiplication.

Monoid of All Nonnegative Matrices

Consider the set of all square matrices with elements in [0:+∞] over a fixed index range. This set forms a monoid with zero with respect to distance multiplication. The identity and the zero element in this monoid are respectively the matrices

for all i, j. For any matrix A, we have

Monge Monoid

It is well-known (see e.g. [6]) that the set of all Monge matrices is closed under distance multiplication.

Theorem 2

Let A, B, C be matrices, such that A⊙B=C. If A, B are Monge, then C is also Monge.

Proof

Let A, B be over [0:n ₁∣0:n ₂], [0:n ₂∣0:n ₃], respectively. Let i′,i″∈[0:n ₁], i′≤i″, and k′,k″∈[0:n ₃], k′≤k″. By definition of matrix distance multiplication, we have

$$\begin{aligned} &C\bigl(i',k''\bigr) = \min _j \bigl(A\bigl(i',j\bigr) + B \bigl(j,k''\bigr)\bigr) \\ &C\bigl(i'',k'\bigr) = \min _j \bigl(A\bigl(i'',j\bigr) + B \bigl(j,k'\bigr)\bigr) \end{aligned}$$

Let j′, j″ respectively be the values of j on which these minima are attained. Suppose j′≤j″. We have

$$\begin{aligned} &C\bigl(i',k'\bigr) + C\bigl(i'',k'' \bigr)\quad \mbox{(definition of $\odot$)} \\ &\quad{}=\min_j \bigl(A\bigl(i',j\bigr) + B \bigl(j,k'\bigr)\bigr) + \min_j \bigl(A \bigl(i'',j\bigr) + B\bigl(j,k'' \bigr)\bigr)\quad \mbox{(minimisation over $j$)} \\ &\quad{}\leq\bigl(A\bigl(i',j'\bigr) + B \bigl(j',k'\bigr)\bigr) + \bigl(A\bigl(i'',j'' \bigr) + B\bigl(j'',k''\bigr) \bigr) \quad \mbox{(term rearrangement)} \\ &\quad{}=\bigl(A\bigl(i',j'\bigr) + A \bigl(i'',j''\bigr)\bigr) + \bigl(B\bigl(j',k'\bigr) + B\bigl(j'',k'' \bigr)\bigr) \quad \mbox{($A$ is Monge)} \\ &\quad{}\leq\bigl(A\bigl(i',j''\bigr) + A \bigl(i'',j'\bigr)\bigr) + \bigl(B \bigl(j',k'\bigr) + B\bigl(j'',k'' \bigr)\bigr) \quad \mbox{(term rearrangement)} \\ &\quad{}=\bigl(A\bigl(i',j''\bigr) + B \bigl(j'',k''\bigr)\bigr) + \bigl(A\bigl(i'',j'\bigr) + B \bigl(j',k'\bigr)\bigr)\quad \mbox{(definition of $j'$, $j''$)} \\ &\quad{}=C\bigl(i',k''\bigr) + C \bigl(i'',k'\bigr) \end{aligned}$$

The case j′≥j″ is treated symmetrically, making use of the Monge property of B. Hence, matrix C is Monge. □

Theorem 2 implies that the set of all square nonnegative Monge matrices over a fixed index range forms a submonoid (the Monge monoid) in the distance multiplication monoid of all nonnegative matrices (where the range of elements has to be formally extended by +∞).

The ambient monoid’s identity Id _⊙ and zero O _⊙ are inherited by the Monge monoid. Indeed, in the expansion of their density matrices $\mathit{Id}_{\odot}^{\square}$ and $O_{\odot}^{\square}$ by Definition 2, all indeterminate expressions of the form +∞−∞ can be formally considered to be nonnegative. Therefore, matrices Id _⊙ and O _⊙ can be formally considered to be Monge matrices.

Unit-Monge Monoid

It is somewhat surprising, but crucial for the development of our techniques, that the set of all simple (sub)unit-Monge matrices is also closed under distance multiplication.

Theorem 3

Let A, B, C be matrices, such that A⊙B=C. If A, B are simple unit-Monge (respectively, simple subunit-Monge), then C is also simple unit-Monge (respectively, simple subunit-Monge).

Proof

Let A, B be simple unit-Monge matrices over [0:n∣0:n]. We have $A = P_{A}^{\varSigma}$, $B = P_{B}^{\varSigma}$, where P _A , P _B are permutation matrices. It is easy to check that matrix C is simple, therefore $C = P_{C}^{\varSigma}$ for some matrix P _C .

We now have $P_{A}^{\varSigma}\odot P_{B}^{\varSigma}= P_{C}^{\varSigma}$, and we need to show that P _C is a permutation matrix. Clearly, matrices C and P _C are both integer. Furthermore, matrix C is Monge by Theorem 2, and therefore matrix C ^□=P _C is nonnegative.

Since P _B is a permutation matrix, we have

for all j∈[0:n]. Hence

$$\begin{aligned} &C(i,0) = \min_j \bigl(P_A^\varSigma(i,j) + P_B^\varSigma(j,0)\bigr) = \min_j \bigl(P_A^\varSigma(i,j) + 0\bigr) = 0 \\ &C(i,n) = \min_j \bigl(P_A^\varSigma(i,j) + P_B^\varSigma(j,n)\bigr) = \min_j \bigl(P_A^\varSigma(i,j) + n - j\bigr) = n-i \end{aligned}$$

for all i∈[0:n], since the minimum is attained respectively at j=0 and j=n. Therefore, we have

$$\begin{aligned} &\sum_{\hat{k}} P_C(\hat{\imath},\hat{k}) \quad \mbox{(definition of $\varSigma$ and $\square$)} \\ &\quad{}=\sum_{\hat{k}} \bigl(C\bigl(\hat{\imath}^+, \hat{k}^-\bigr) - C\bigl(\hat{\imath}^-,\hat{k}^-\bigr) - C\bigl(\hat{\imath}^+, \hat{k}^+\bigr) + C\bigl(\hat{\imath}^-,\hat{k}^+\bigr)\bigr)\quad \mbox{(term cancellation)} \\ &\quad{}=C\bigl(\hat{\imath}^+,0\bigr) - C\bigl(\hat{\imath}^-,0\bigr) - C\bigl( \hat{\imath}^+,n\bigr) + C\bigl(\hat{\imath}^-,n\bigr) \\ &\quad{}= 0 - 0 - \bigl(n-\hat{\imath}^+\bigr) + \bigl(n-\hat{\imath}^-\bigr) = 1 \end{aligned}$$

for all $\hat{\imath}\in\langle{0:n}\rangle$. Symmetrically, we have

for all $\hat{k}\in\langle{0:n}\rangle$. Taken together, the above properties imply that matrix P _C is a permutation matrix. Therefore, C is a simple unit-Monge matrix.

Finally, let A, B be simple subunit-Monge matrices over [0:n ₁∣0:n ₂], [0:n ₂∣0:n ₃], respectively. We have $A = P_{A}^{\varSigma}$, $B = P_{B}^{\varSigma}$, where P _A , P _B are subpermutation matrices. As before, let $C=P_{C}^{\varSigma}$, for some matrix P _C ; we have to show that P _C is a subpermutation matrix. Suppose that for some $\hat{\imath}$, row $P_{A}(\hat{\imath},*)$ contains only zeros. Then, it is easy to check that the corresponding row $P_{C}(\hat{\imath},*)$ also contains only zeros, and that upon deleting rows $P_{A}(\hat{\imath},*)$ and $P_{C}(\hat {\imath},*)$ from the respective matrices, the equality $P_{A}^{\varSigma}\odot P_{B}^{\varSigma}= P_{C}^{\varSigma}$ still holds. Symmetrically, a zero column $P_{B}(*,\hat{k})$ results in a zero column $P_{C}(*,\hat{k})$, and upon deleting both these columns from the respective matrices, the equality $P_{A}^{\varSigma}\odot P_{B}^{\varSigma}= P_{C}^{\varSigma}$ still holds. Therefore, we may assume without loss generality that n ₁≤n ₂, n ₂≥n ₃, and that subpermutation matrix P _A (respectively, P _B ) does not have any zero rows (respectively, zero columns).

Let us now extend matrix P _A to a square n ₂×n ₂ matrix , where the top n ₂−n ₁ rows are filled by zeros and ones so that the resulting matrix is a permutation matrix. Likewise, let us extend matrix P _B to an n ₂×n ₂ permutation matrix . We now have

where is an n ₂×n ₂ permutation matrix, with matrix P _C occupying its lower-left corner. Hence, matrix P _C is a subpermutation matrix, and the original matrix C is a simple subunit-Monge matrix. □

Theorem 3 implies that the set of all simple unit-Monge matrices over a fixed index range forms a submonoid (the unit-Monge monoid) in the Monge monoid.

Without loss of generality, let the matrices be over [0:n∣0:n]. The Monge monoid’s identity Id _⊙ and zero O _⊙ are neither simple nor unit-Monge matrices, and therefore are not inherited by the unit-Monge monoid. Instead, its identity and zero elements are given respectively by the matrices

(recall that Id ^R is the matrix obtained by 90-degree rotation of the identity permutation matrix Id). For any permutation matrix P, we have

Theorem 3 gives us the basis for performing distance multiplication of simple (sub)unit-Monge matrices implicitly, by taking the density (sub)permutation matrices as input, and producing a density (sub)permutation matrix as output. It will be convenient to introduce special notation for such implicit distance matrix multiplication.

Definition 8

Let P _A , P _B , P _C be (sub)permutation matrices. The implicit matrix distance product P _A ⊡P _B =P _C is defined by $P_{A}^{\varSigma}\odot P_{B}^{\varSigma}= P_{C}^{\varSigma}$.

The set of all permutation matrices over 〈0:n∣0:n〉 is therefore a monoid with respect to implicit distance multiplication ⊡. This monoid has identity element Id and zero element Id ^R, and is isomorphic to the unit-Monge monoid. Note that, although defined on the set of all permutation matrices of size n, this monoid is substantially different from the symmetric group $\mathcal{S}_{n}$, defined by standard permutation composition (equivalently, by standard multiplication of permutation matrices). In particular, the implicit distance multiplication monoid has a zero element Id ^R, whereas $\mathcal{S}_{n}$, being a group, cannot have a zero. More generally, the implicit distance multiplication monoid has plenty of idempotent elements (defined by involutive permutations), whereas $\mathcal{S}_{n}$ has the only trivial idempotent Id. However, both the implicit distance multiplication monoid and the symmetric group $\mathcal{S}_{n}$ still share the same identity element Id.

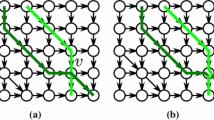
Example

Figure 1a shows a triple of 6×6 permutation matrices P _A , P _B , P _C , such that P _A ⊡P _B =P _C . Nonzeros are indicated by green² circles.

Fig. 1

Implicit matrix distance product P _A ⊡P _B =P _C

3.2 Seaweed Braids

Further understanding of the unit-Monge monoid (and, by isomorphism, of the implicit distance multiplication monoid of permutation matrices) can be gained via an algebraic formalism closely related to braid theory. While this formalism is not necessary for obtaining the main results of this paper, we believe it to be of substantial independent interest. We refer the reader to [38] for the background on classical braid theory.

Consider two sets of n nodes each, drawn on two parallel horizontal lines in the Euclidean plane. We put the two node sets into one-to-one correspondence by connecting them pairwise, in some order, with continuous monotone curves. (Here, a curve is called monotone, if its vertical projection is always directed downwards.) These curves will be called seaweeds.³ We call the resulting configuration a seaweed braid of width n.

Example

Figure 1b shows three different seaweed braids.

There is remarkable similarity between seaweed braids and classical braids. However, there is also a crucial difference: all crossings between seaweeds are “level crossings”, i.e. a pair of crossing seaweeds are not assumed to pass under/over one another as in classical braids. We will also assume that all crossings are between exactly two seaweeds, hence three or more seaweeds can never meet at a single point.

In a seaweed braid, a given pair of seaweeds may cross an arbitrary number of times. We call a seaweed braid reduced, if every pair of its seaweeds cross at most once (i.e. either once, or not at all).

Similarly to classical braids, two seaweed braids of the same width can be multiplied. The product braid is obtained as follows. First, we draw one braid above the other, identifying the bottom nodes of the top braid with the top nodes of the bottom braid. Then, we join up each pair of seaweeds that became incident in the previous step. Note that, even if both original seaweed braids were reduced, their product may in general not be reduced.

Example

In Fig. 1b, the left-hand side is a product of two reduced seaweed braids. In this product braid, some pairs of seaweeds cross twice, hence it is not reduced.

Seaweed braids can be transformed (and, in particular, unreduced braids can be reduced) according to a specific set of algebraic rules. These rules are incorporated into the following formal definition.

Definition 9

The seaweed monoid $\mathcal{T}_{n}$ is a finitely presented monoid on n generators: id (the identity element), g ₁, g ₂, …, g _n−1. The presentation of monoid $\mathcal{T}_{n}$ consists of the idempotence relations

$$\begin{aligned} g_t^2 = g_t \quad t \in[1:n-1] \end{aligned}$$

(1)

the far commutativity relations

$$\begin{aligned} g_t g_u = g_u g_t\quad t,u \in[1:n-1],\ u-t \geq2 \end{aligned}$$

(2)

and the braid relations

$$\begin{aligned} g_t g_u g_t = g_u g_t g_u\quad t,u \in[1:n-1], u-t = 1 \end{aligned}$$

(3)

Traditionally, this structure is also known as the 0-Hecke monoid of the symmetric group $H_{0}(\mathcal{S}_{n})$, or the Richardson–Springer monoid (for details, see e.g. Denton et al. [20], Mazorchuk and Steinberg [49], Deng et al. [19]).

The correspondence between elements of the seaweed monoid and seaweed braids is as follows. The monoid multiplication (i.e. concatenation of words in the generators) corresponds to the multiplication of seaweed braids. The identity element id corresponds to a seaweed braid where the top nodes are connected to the bottom nodes in the left-to-right order, without any crossings. Each of the remaining generators g _t corresponds to an elementary crossing, i.e. to a seaweed braid where the only crossing is between a pair of neighbouring seaweeds in half-integer positions t ⁻ and t ⁺. Figure 2 shows the defining relations of the seaweed monoid (1)–(3) in terms of seaweed braids.

Fig. 2

Defining relations of the seaweed monoid

Example

In Fig. 1b, the left-hand side is an unreduced product of two seaweed braids. We now comb the seaweeds by running through all their crossings, respecting the top-to-bottom partial order of the crossings. For each crossing, we check whether the two crossing seaweeds have previously crossed above the current point. If this is the case, then we undo the current crossing by removing it from the braid and replacing it by two non-crossing seaweed pieces. The correctness of this combing procedure is easy to prove by the seaweed monoid relations (1)–(3). After all the crossings have been combed, we obtain a reduced seaweed braid shown in the middle of Fig. 1b. Another equivalent reduced seaweed braid in shown in the right-hand side.

A permutation matrix P over 〈0:n∣0:n〉 can be represented by a seaweed braid as follows. The row and column indices correspond respectively to the top and the bottom nodes, ordered from left to right. A nonzero $P(\hat{\imath},\hat{\jmath})=1$ corresponds to a seaweed connecting top node $\hat{\imath}$ and bottom node $\hat{\jmath}$. For a given permutation, it is always possible to draw the seaweeds so that the resulting seaweed braid is reduced. In general, this reduced braid will not be unique; however, it turns out that all the reduced braids corresponding to the same permutation are equivalent. We formalise this observation by the following lemma.

Lemma 1

The seaweed monoid $\mathcal{T}_{n}$ consists of at most n! distinct elements.

Proof

It is straightforward to see that any seaweed braid can be transformed into a reduced one, using relations (1)–(3). Then, any two reduced seaweed braids corresponding to the same permutation can be transformed into one another, using far commutativity (2) and the braid relations (3). Therefore, each permutation corresponds to a single element of $\mathcal{T}_{n}$. This mapping is surjective, therefore the number of elements in $\mathcal{T}_{n}$ is at most the total number of permutations n!. □

We now establish a direct connection between elements of the seaweed monoid and permutation matrices. The identity generator id corresponds to the identity matrix Id. Each of the remaining generators g _t corresponds to an elementary transposition matrix G _t , defined as

Lemma 2

The set $\{G_{t}^{\varSigma}\}$, t∈[1:n−1], generates the full distance multiplication monoid of simple unit-Monge matrices.

Proof

Let P be a permutation matrix. Consider an arbitrary reduced seaweed braid corresponding to P, and let t be the position of its first elementary crossing. Consider the truncated seaweed braid, obtained by removing this seaweed crossing. This braid is still reduced, and such that the pair of seaweeds originating in t ⁻, t ⁺ do not cross. Let this pair of seaweeds terminate at indices $\hat{k}_{0}$, $\hat{k}_{1}$, where $\hat{k}_{0} < \hat{k}_{1}$. Let Q be the permutation matrix corresponding to the truncated seaweed braid. We have

$$\begin{aligned} &P\bigl(t^-,\hat{k}_1\bigr) = P\bigl(t^+, \hat{k}_0\bigr) = 1 \\ &Q\bigl(t^-,\hat{k}_0\bigr) = Q\bigl(t^+,\hat{k}_1 \bigr) = 1 \end{aligned}$$

We will now show that P=G _t ⊡Q or, equivalently $P^{\varSigma}= G_{t}^{\varSigma}\odot Q^{\varSigma}$. The lemma statement then follows by induction.

Note that $G_{t}^{\varSigma}(i,j) = \mathit{Id}^{\varSigma}(i,j)$ and Q ^Σ(i,j)=P ^Σ(i,j) for all i∈[0:n], i≠t, and for all j∈[0:n]. Therefore, we have

for all i∈[0:n], i≠t, and for all k∈[0:n].

It remains to consider the case i=t. Note that $G_{t}^{\varSigma}(t,j) = \mathit{Id}^{\varSigma}(t,j)$ for all j∈[0:n], j≠t. Let k∈[0:n]. We have

(4)

By definition of the distribution matrix (Definition 1), we have

$$\begin{aligned} &G_t^\varSigma(t,t-1) = 0 \\ &G_t^\varSigma(t,t) = G_t^\varSigma(t,t+1) = 1 \\ &0 \leq Q^\varSigma(t-1,k) - Q^\varSigma(t,k) \leq1 \\ &0 \leq Q^\varSigma(t,k) - Q^\varSigma(t+1,k) \leq1 \end{aligned}$$

Hence, we have

$$\begin{aligned} G_t^\varSigma(t,t) + Q^\varSigma(t,k) =& 1 + Q^\varSigma(t,k) \\ \geq& 0 + Q^\varSigma(t-1,k) = G_t^\varSigma(t,t-1) + Q^\varSigma(t-1,k) \end{aligned}$$

and, analogously,

We have established that the value under the minimum operator in (4) for j=t is always no less than the values for both j=t−1 and j=t+1. Therefore, the minimum is never attained solely at j=t, so we may assume j≠t. We now consider two cases: either j∈[0:t−1], or j∈[t+1:n].

For j∈[0:t−1], we have $G_{t}^{\varSigma}(t,j) = 0$. Therefore,

$$\begin{aligned} &\min_{j \in[0:t-1]} \bigl(G_t^\varSigma(t,j) + Q^\varSigma(j,k)\bigr) \\ &\quad{}=\min_{j \in[0:t-1]} \bigl(0 + Q^\varSigma(j,k)\bigr) \quad\mbox{(attained at $j=t-1$)} \\ &\quad{}=Q^\varSigma(t-1,k) = P^\varSigma(t-1,k) \end{aligned}$$

Similarly, for j∈[t+1:n], we have $G_{t}^{\varSigma}(t,j) = j-t$. Therefore,

$$\begin{aligned} &\min_{j \in[t+1:n]} \bigl(G_t^\varSigma(t,j) + Q^\varSigma(j,k)\bigr) \\ &\quad{}=\min_{j \in[t+1:n]} \bigl(j-t + Q^\varSigma(j,k)\bigr) \quad\mbox{(attained at $j=t+1$)} \\ &\quad{}=1 + Q^\varSigma(t+1,k) = 1 + P^\varSigma(t+1,k) \end{aligned}$$

Substituting into (4), we now have

Recall that $P(t^{-},\hat{k}_{1}) = P(t^{+},\hat{k}_{0}) = 1$. We have

$$\begin{aligned} &P^\varSigma(t-1,k) = P^\varSigma(t,k) = P^\varSigma(t+1,k) \quad \text{for $k < \hat{k}_{0}$} \\ &P^\varSigma(t-1,k) = P^\varSigma(t,k) = 1 + P^\varSigma(t+1,k) \quad \text{for $\hat{k}_{0} < k < \hat{k}_{1}$} \\ &P^\varSigma(t-1,k) - 1 = P^\varSigma(t,k) = 1 + P^\varSigma(t+1,k) \quad \text{for $\hat{k}_{1} < k$} \end{aligned}$$

In all three above cases, we have

which completes the proof. □

We are now able to establish a formal connection between the unit-Monge monoid and the seaweed monoid.

Theorem 4

The distance multiplication monoid of n×n simple unit-Monge matrices is isomorphic to the seaweed monoid $\mathcal{T}_{n}$.

Proof

We have already established a bijection between the generators of both monoids: a generator simple unit-Monge matrix $G_{t}^{\varSigma}$ corresponds to a generator g _t of the seaweed monoid $\mathcal{T}_{n}$. It is straightforward to check that relations (1)–(3) are verified by matrices $G_{t}^{\varSigma}$, therefore the bijection on the generators defines a homomorphism from the seaweed monoid to the unit-Monge matrix monoid. By Lemma 2, this homomorphism is surjective, hence the cardinality of $\mathcal{T}_{n}$ is at least the number of all simple unit-Monge matrices of size n, equal to n!. However, by Lemma 1, the cardinality of $\mathcal{T}_{n}$ is at most n!. Thus, the cardinality of $\mathcal{T}_{n}$ is exactly n!, and the two monoids are isomorphic. □

Example

In Fig. 1, the seaweed braids shown in Fig. 1b correspond to the implicit matrix distance product P _A ⊡P _B =P _C in Fig. 1a.

The seaweed monoid is closely related to some other well-known algebraic structures:

• by replacing the idempotence relations (1) with involution relations $g_{t}^{2} = \mathit{id}$, we obtain the Coxeter presentation of the symmetric group;

• by removing the idempotence relations (1), and keeping far commutativity (2) and braid relations (3), we obtain the classical positive braid monoid (see e.g. [38, Sect. 6.5]);

• by removing the braid relations (3), and keeping idempotence (1) and far commutativity (2), we obtain the locally free idempotent monoid [67] (see also [24]);

• by introducing the generators’ inverses $g_{t}^{-1}$, and replacing the idempotence relations (1) with cancellation relations $g_{t} g_{t}^{-1} = \mathit{id}$, we obtain the classical braid group.

A generalisation of the seaweed monoid is given by 0-Hecke monoids of general Coxeter groups, also known as Coxeter monoids. These monoids arise naturally as subgroup monoids in groups. The theory of Coxeter monoids can be traced back to Bourbaki [11], and was developed in [12, 26, 53, 66]. A further generalisation to $\mathcal{J}$ -trivial monoids has been studied by Denton et al. [20]. The contents of this and the following sections can be regarded as the first step in the algorithmic study of such general classes of monoids.

3.3 Fast Implicit Distance Multiplication

For generic, explicitly presented matrices, direct application of Definition 7 gives an algorithm for matrix distance multiplication of size n, running in time O(n ³). Slightly subcubic algorithms for this problem have also been obtained. The fastest currently known algorithm is by Chan [15], running in time $O(\frac{n^{3} (\log\log n)^{3}}{\log^{2} n})$.

For Monge matrices, distance multiplication can easily be performed in time O(n ²), using the standard row-minima searching technique of Aggarwal et al. [1] to perform matrix-vector multiplication in linear time (see also [6, 57]). Alternatively, an algorithm with the same quadratic running time can be obtained directly by the divide-and-conquer technique (see e.g. [5]).

While the quadratic running time is trivially optimal for explicit matrices, it is possible to break through this time barrier in the case of implicitly represented matrices. Subquadratic distance multiplication algorithms for implicit simple (sub)unit-Monge matrices were given in [58, 61], running in time O(n ^1.5). We now show an even faster algorithm for this problem.

Theorem 5

Let P _A , P _B , P _C be n×n permutation matrices, such that P _A ⊡P _B =P _C . Given the nonzeros of P _A , P _B , the nonzeros of P _C can be computed in time O(nlogn).

Proof

Let P _A , P _B , P _C be permutation matrices over 〈0:n∣0:n〉. The algorithm follows a divide-and-conquer approach, in the form of recursion on n.

Recursion base: n=1.:

The computation is trivial.

Recursive step: n>1.:

Assume without loss of generality that n is even. Informally, the idea is to split the range of index j in the definition of matrix distance product (Definition 7) into two sub-intervals of size $\frac{n}{2}$. For each of these half-sized sub-intervals of j, we use the sparsity of the input permutation matrix P _A (respectively, P _B ) to reduce the range of index i (respectively, k) to a (not necessarily contiguous) subset of size $\frac{n}{2}$; this completes the divide phase. We then call the algorithm recursively on the two resulting half-sized subproblems. Using the subproblem solutions, we reconstruct the output permutation matrix P _C ; this is the conquer phase.

We now describe each phase of the recursive step in more detail.

Divide phase.:

By Definition 8, we have

Consider the partitioning of matrices P _A , P _B into subpermutation matrices

where P _A,lo , P _A,hi , P _B,lo , P _B,hi are over $\langle{0:n \mid0:\frac{n}{2}}\rangle$, $\langle{0:n \mid\frac{n}{2}:n}\rangle$, $\langle{0:\frac{n}{2} \mid0:n}\rangle$, $\langle{\frac{n}{2}:n \mid0:n}\rangle$, respectively; in each of these matrices, we maintain the indexing of the original matrices P _A , P _B . We now have two implicit matrix multiplication subproblems

where P _C,lo , P _C,hi are of size n×n. Each of the subpermutation matrices P _A,lo , P _A,hi , P _B,lo , P _B,hi , P _C,lo , P _C,hi has exactly $\frac{n}{2}$ nonzeros.

Recall from the proof of Theorem 3 that a zero row in P _A,lo (respectively, a zero column in P _B,lo ) corresponds to a zero row (respectively, column) in their implicit distance product P _C,lo . Therefore, we can delete all zero rows and columns from P _A,lo , P _B,lo , P _C,lo , obtaining, after appropriate index remapping, three $\frac{n}{2} \times\frac{n}{2}$ permutation matrices. Consequently, the first subproblem can be solved by first performing a linear-time index remapping (corresponding to the deletion of zero rows and columns from P _A,lo , P _B,lo ), then making a recursive call on the resulting half-sized problem, and then performing an inverse index remapping (corresponding to the reinsertion of the zero rows and columns into P _C,lo ). The second subproblem can be solved analogously.

Conquer phase.:

We now need to combine the solutions for the two subproblems to a solution for the original problem. Note that we cannot simply put together the nonzeros of the subproblem solutions. The original problem depends on the subproblems in a more subtle way: some elements of $P_{A}^{\varSigma}$ depend on elements of both P _A,lo and P _A,hi , and therefore would not be accounted for directly by the solution to either subproblem on its own. A similar observation holds for elements of $P_{B}^{\varSigma}$. However, note that the nonzeros in the two subproblems have disjoint index ranges, and therefore the direct combination of subproblem solutions P _C,lo +P _C,hi , although not a solution to the original problem, is still a permutation matrix.

In order to combine correctly the solutions of the two subproblems, let us consider the relationship between these subproblems in more detail. First, we split the range of index j in the definition of matrix distance product (Definition 7) into a “low” and a “high” sub-interval, each of size $\frac{n}{2}$.

$$\begin{aligned} P_C^\varSigma(i,k) &= \min_{j \in[0:n]} \bigl(P_A^\varSigma(i,j) + P_B^\varSigma(j,k) \bigr) \\ &= \min\Bigl( \min_{j \in[0:\frac{n}{2}]} \bigl(P_A^\varSigma(i,j) + P_B^\varSigma(j,k)\bigr), \min_{j \in[\frac{n}{2}:n]} \bigl(P_A^\varSigma(i,j) + P_B^\varSigma(j,k) \bigr)\Bigr) \end{aligned}$$

(5)

for all i,k∈[0:n]. Let us denote the two arguments in (5) by M _lo (i,k) and M _hi (i,k), respectively:

(6)

for all i,k∈[0:n]. The first argument in (5), (6) can be expressed via the solutions of the two subproblems as follows:

$$\begin{aligned} M_{\mathit{lo}}(i,k) =& \min_{j \in[0:\frac{n}{2}]} \bigl(P_A^\varSigma(i,j) + P_B^\varSigma(j,k) \bigr) \quad\mbox{(definition of $\varSigma$)} \\ =&\min_{j \in[0:\frac{n}{2}]} \biggl(P_{A,\mathit{lo}}^\varSigma(i,j) + P_{B,\mathit{lo}}^\varSigma(j,k) + P_{B,\mathit{hi}}^\varSigma\biggl( \frac{n}{2},k\biggr)\biggr) \\ &\mbox{(term rearrangement)} \\ =& \min_{j \in[0:\frac{n}{2}]} \bigl(P_{A,\mathit{lo}}^\varSigma(i,j) + P_{B,\mathit{lo}}^\varSigma(j,k)\bigr) + P_{B,\mathit{hi}}^\varSigma \biggl(\frac{n}{2},k\biggr) \\ &\mbox{(definition of $\odot$)} \\ =& P_{C,\mathit{lo}}^\varSigma(i,k) + P_{C,\mathit{hi}}^\varSigma(0,k) \end{aligned}$$

(7)

Here, the final equality is due to

$$\begin{aligned} P_{C,\mathit{hi}}^\varSigma(0,k) =& \min_{j \in[\frac{n}{2}:n]} \bigl(P_{A,\mathit{hi}}^\varSigma(0,j) + P_{B,\mathit{hi}}^\varSigma(j,k) \bigr) \\ =&\min_{j \in[\frac{n}{2}:n]} \biggl(j - \frac{n}{2} + P_{B,\mathit{hi}}^\varSigma(j,k)\biggr) = P_{B,\mathit{hi}}^\varSigma \biggl(\frac{n}{2},k\biggr) \end{aligned}$$

since the minimum is attained at $j = \frac{n}{2}$. The second argument in (5), (6) can be expressed analogously as

$$\begin{aligned} M_{\mathit{hi}}(i,k) =& \min_{j \in[\frac{n}{2}:n]} \bigl(P_A^\varSigma(i,j) + P_B^\varSigma(j,k) \bigr) \\ =&P_{C,\mathit{hi}}^\varSigma(i,k) + P_{C,\mathit{lo}}^\varSigma(i,n) \end{aligned}$$

(8)

The minimisation operator in (5), (6) is equivalent to evaluating the sign of the difference of its two arguments:

$$\begin{aligned} \delta(i,k) =& M_{\mathit{lo}}(i,k) - M_{\mathit{hi}}(i,k) \quad \mbox{(by (7), (8))} \\ =&\bigl(P_{C,\mathit{lo}}^\varSigma(i,k) + P_{C,\mathit{hi}}^\varSigma(0,k) \bigr) - \bigl(P_{C,\mathit{hi}}^\varSigma(i,k) + P_{C,\mathit{lo}}^\varSigma(i,n) \bigr) \\ &\mbox{(term rearrangement)} \\ =&\bigl(P_{C,\mathit{hi}}^\varSigma(0,k) - P_{C,\mathit{hi}}^\varSigma(i,k) \bigr) - \bigl(P_{C,\mathit{lo}}^\varSigma(i,n) - P_{C,\mathit{lo}}^\varSigma(i,k) \bigr) \\ &\mbox{(definition of $\varSigma$)} \\ =&\sum_{\hat{\imath}\in\langle{0:i}\rangle,\hat{k}\in\langle {0:k}\rangle} P_{C,\mathit{hi}}(\hat{ \imath},\hat{k}) - \sum_{\hat{\imath}\in\langle{i:n}\rangle,\hat{k}\in\langle {k:n}\rangle} P_{C,\mathit{lo}}(\hat{ \imath},\hat{k}) \\ &\mbox{(definition of $\varSigma$, $R$)} \\ =&P_{C,\mathit{hi}}^{R\varSigma}(n-k,i) - P_{C,\mathit{lo}}^{RRR\varSigma}(k,n-i) \end{aligned}$$

Since P _C,lo , P _C,hi are subpermutation matrices, and P _C,lo +P _C,hi a permutation matrix, it follows that function δ is unit-monotone increasing in each of its arguments.

The sign of function δ determines the positions of nonzeros in P _C as follows. Let us fix some half-integer point $\hat{\imath},\hat{k}\in\langle {0:n}\rangle$ in P _C , and consider the signs of the four values $\delta(\hat{\imath}^{\pm},\hat{k}^{\pm})$ at neighbouring integer points. Due to the unit-monotonicity of δ, only three cases are possible.

Case $\delta(\hat{\imath}^{\pm},\hat{k}^{\pm}) \leq0$ for all four sign combinations.:

We have

for each sign combination taken consistently on both sides of the inequality, and, by (6),

Hence, we have

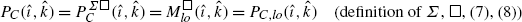
Thus, in this case $P_{C}(\hat{\imath},\hat{k}) = 1$ is equivalent to $P_{C,\mathit{lo}}(\hat{\imath},\hat{k}) = 1$. Note that this also implies $\delta(\hat{\imath}^{-},\hat{k}^{-}) < 0$, since otherwise we would have $\delta(\hat{\imath}^{\pm},\hat{k}^{\pm}) = 0$ for all four sign combinations, and hence, by symmetry, also $P_{C,\mathit{hi}}(\hat{\imath},\hat {k}) = 1$. However, that would imply $P_{C,\mathit{lo}}(\hat{\imath},\hat {k})+P_{C,\mathit{hi}}(\hat{\imath},\hat{k}) = 1+1 = 2$, which is a contradiction to P _C,lo +P _C,hi being a permutation matrix.

Case $\delta(\hat{\imath}^{\pm},\hat{k}^{\pm}) \geq0$ for all four sign combinations.:

Symmetrically to the previous case, we have

Thus, in this case $P_{C}(\hat{\imath},\hat{k}) = 1$ is equivalent to $P_{C,\mathit{lo}}(\hat{\imath},\hat{k}) = 1$, and implies $\delta(\hat{\imath}^{+},\hat{k}^{+}) > 0$.

Case $\delta(\hat{\imath}^{-},\hat{k}^{-}) < 0$, $\delta(\hat{\imath}^{-},\hat{k}^{+}) = \delta(\hat{\imath}^{+},\hat {k}^{-}) = 0$, $\delta(\hat{\imath}^{+},\hat{k}^{+}) > 0$.:

By (6), we have

$$\begin{aligned} &P_C^\varSigma\bigl(\hat{\imath}^-,\hat{k}^-\bigr) = M_{\mathit{lo}}\bigl(\hat {\imath}^-,\hat{k}^-\bigr) \\ &P_C^\varSigma\bigl(\hat{\imath}^+,\hat{k}^-\bigr) = M_{\mathit{lo}}\bigl(\hat {\imath}^+,\hat{k}^-\bigr) \\ &P_C^\varSigma\bigl(\hat{\imath}^-,\hat{k}^+\bigr) = M_{\mathit{lo}}\bigl(\hat {\imath}^-,\hat{k}^+\bigr) \\ &P_C^\varSigma\bigl(\hat{\imath}^+,\hat{k}^+\bigr) = M_{\mathit{hi}}\bigl(\hat {\imath}^+,\hat{k}^+\bigr) < M_{\mathit{lo}}\bigl( \hat{\imath}^+,\hat{k}^+\bigr) \end{aligned}$$

Hence,

Since both P _C and P _C,lo are zero-one matrices, the strict inequality implies that $P_{C}(\hat{\imath},\hat{k})=1$ and $P_{C,\mathit{lo}}(\hat{\imath},\hat{k})=0$. Symmetrically, also $P_{C,\mathit{hi}}(\hat{\imath},\hat{k})=0$.

Summarising the above three cases, we have $P_{C}(\hat{\imath},\hat{k})=1$, if and only if one of the following conditions holds:

$$\begin{aligned} &\delta\bigl(\hat{\imath}^-,\hat{k}^-\bigr) < 0\quad \mbox{and}\quad P_{C,\mathit{lo}}(\hat{\imath},\hat{k})=1 \end{aligned}$$

(9)

$$\begin{aligned} &\delta\bigl(\hat{\imath}^+,\hat{k}^+\bigr) > 0\quad \mbox{and}\quad P_{C,\mathit{hi}}(\hat{\imath},\hat{k})=1 \end{aligned}$$

(10)

$$\begin{aligned} &\delta\bigl(\hat{\imath}^-,\hat{k}^-\bigr) < 0\quad \mbox{and}\quad \delta\bigl( \hat{\imath}^+,\hat{k}^+\bigr) > 0 \end{aligned}$$

(11)

By the discussion above, these three conditions are mutually exclusive.

In order to check the conditions (9)–(11), we need an efficient procedure for determining the sign of function δ in points of the integer square [0:n∣0:n]. Informally, low (respectively, high) values of both i and k correspond to negative (respectively, positive) values of δ(i,k). By unit-monotonicity of δ, there must exist a pair of monotone rectilinear paths from the bottom-left to the top-right corner of the half-integer square 〈−1:n+1∣−1:n+1〉, that separate strictly negative and nonnegative (respectively, strictly positive and nonpositive) values of δ.

We now give a simple efficient procedure for finding such a pair of separating paths. By symmetry we only need to the consider the lower separating path. For all integer points (i,k) above-left (respectively, below-right) of this path, we have δ(i,k)<0 (respectively, δ(i,k)≥0).

We start at the bottom-left corner of the square, with $(\hat{\imath},\hat{k}) = (n^{+},0^{-})$ as the initial point on the lower separating path. We have $\delta(\hat{\imath}^{-},\hat{k}^{+}) = \delta(n,0) = 0$.

Let $(\hat{\imath},\hat{k})$ now denote any current point on the lower separating path, and suppose that we have evaluated $\delta(\hat{\imath}^{-},\hat{k}^{+})$. The sign of this value determines the next point on the path:

$$\begin{aligned} &(\hat{\imath},\hat{k}+1) \quad\text{if } \delta\bigl(\hat{\imath}^-,\hat{k}^+ \bigr) < 0 \\ &(\hat{\imath}-1,\hat{k}) \quad\text{if } \delta\bigl(\hat{\imath}^-,\hat{k}^+ \bigr) \geq0 \end{aligned}$$

Following this choice, we then evaluate either $\delta(\hat{\imath}^{-},(\hat{k}+1)^{+})$, or $\delta((\hat {\imath}-1)^{-},\hat{k}^{+})$ from $\delta(\hat{\imath}^{-},\hat{k}^{+})$ by an incremental query of Theorem 1 in time O(1). The computation is now repeated with the new current point.

The described path-finding procedure runs until either $\hat{\imath}= 0^{-}$, or $\hat{k}= n^{+}$. We then complete the path by moving in a straight horizontal (respectively, vertical) line to the final destination $(\hat{\imath},\hat{k}) = (0^{-},n^{+})$. The whole procedure of finding the lower separating path runs in time O(n). A symmetric procedure with the same running time can be used to find the upper separating path, for which we have δ(i,k)≤0 on the above-left, and δ(i,k)>0 on the below-right.

Given a value d∈[−n+1:n−1], let us now consider the set of points $(\hat{\imath},\hat{k})$ with $\hat{k}-\hat{\imath}=d$; such a set forms a diagonal in the half-integer square. Let $(\hat{\imath}_{\mathit{lo}},\hat{k}_{\mathit{lo}})$, where $\hat {k}_{\mathit{lo}}- \hat{\imath}_{\mathit{lo}}= d$, be the unique intersection point of the given diagonal with the lower separating path. Let $r_{\mathit{lo}}(d) = \hat{\imath}_{\mathit{lo}}+ \hat{k}_{\mathit{lo}}$. Define r _hi (d) analogously, using the upper separating path. Conditions (9)–(11) can now be expressed in terms of arrays r _lo , r _hi as follows:

$$\begin{aligned} &\hat{\imath}+\hat{k}\leq r_\mathit{lo}(\hat{k}-\hat{\imath})\quad \mbox{and}\quad P_{C,\mathit{lo}}(\hat{\imath},\hat{k})=1 \end{aligned}$$

(12)

$$\begin{aligned} &\hat{\imath}+\hat{k}\geq r_\mathit{hi}(\hat{k}-\hat{\imath})\quad \mbox{and}\quad P_{C,\mathit{hi}}(\hat{\imath},\hat{k})=1 \end{aligned}$$

(13)

$$\begin{aligned} &\hat{\imath}+\hat{k}= r_\mathit{lo}(\hat{k}-\hat{\imath}) = r_\mathit{hi}(\hat{k}-\hat{\imath}) \end{aligned}$$

(14)

Here, we make use of the fact that $\hat{\imath}+\hat{k}\leq r_{\mathit{lo}}(\hat{k}-\hat{\imath})$ is equivalent to $\hat{\imath}^{-} + \hat{k}^{-} < r_{\mathit{lo}}(\hat {k}-\hat{\imath})$, and $\hat{\imath}+\hat{k}\geq r_{\mathit{hi}}(\hat{k}-\hat{\imath })$ to $\hat{\imath}^{+} + \hat{k}^{+} > r_{\mathit{hi}}(\hat{k}-\hat {\imath})$.

The nonzeros of P _C satisfying either of the conditions (12), (13) can be found in time O(n) by checking directly each of the nonzeros in matrices P _C,lo and P _C,hi . The nonzeros of P _C satisfying condition (14) can be found in time O(n) by a linear sweep of the points $(\hat{\imath},\hat{k})$ on the two separating paths. We have now obtained all the nonzeros of matrix P _C .

(End of recursive step)

Time analysis.:

The recursion tree is a balanced binary tree of height logn. In the root node, the computation runs in time O(n). In each subsequent level, the number of nodes doubles, and the running time per node decreases by a factor of 2. Therefore, the overall running time is O(nlogn).  □

Example

Figure 3 illustrates the proof of Theorem 5 on a problem instance with a solution generated by the Wolfram Mathematica software. Figure 3a shows a pair of input 20×20 permutation matrices P _A , P _B , with nonzeros indicated by green circles. Figure 3b shows the partitioning of the implicit 20×20 matrix distance multiplication problem into two 10×10 subproblems. The nonzeros in the two subproblems are shown respectively by filled red squares and hollow blue squares. Figure 3c shows a recursive step. The lower and the upper separating paths are shown respectively in red and in blue (note that the lower path is visually above the upper one; the lower/upper terminology refers to the relative values of δ, rather than the visual position of the paths). The nonzeros in the output matrix P _C satisfying (12), (13), (14) are shown respectively by filled red squares, hollow blue squares, and green circles; note that overall, there are 20 such nonzeros, and that they define a permutation matrix. Figure 3d shows the output matrix P _C .

Fig. 3

Proof of Theorem 5: P _A ⊡P _B =P _C

Having proved Theorem 5, it is natural to ask whether a similar fast algorithm exists for implicit distance multiplication of general (not necessarily simple) unit-Monge matrices. Unfortunately, there does not appear to be an easy reduction from this more general problem to the case of simple matrices. A related problem is the distance multiplication of an implicit simple unit-Monge matrix by an arbitrary vector. Even this, more basic problem appears to be highly non-trivial. An optimal algorithm for this problem, running in time O(n), was recently given by Gawrychowski [28].

3.4 Bruhat Order

Given a permutation, it is natural to ask how well-sorted it is. In particular, a permutation may be either fully sorted (the identity permutation), or fully anti-sorted (the reverse identity permutation), or anything in between. More generally, given two permutations, it is natural to ask whether, in some sense, one is “more sorted” than the other.

Let P _A , P _B be permutation matrices over 〈0:n∣0:n〉. A classical “degree-of-sortedness” comparison is given by the following partial order (see e.g. Bóna [10], Hammett and Pittel [33], and references therein).

Definition 10

Matrix P _A is lower than matrix P _B in the Bruhat order, P _A ⪯P _B , if P _A can be transformed to P _B by a sequence of anti-sorting steps. Each such step substitutes a (not necessarily contiguous) submatrix of the form by a submatrix of the form .

Informally, P _A ⪯P _B , if P _A defines a “more sorted” permutation than P _B . More precisely, P _A ⪯P _B , if the permutation defined by P _A can be transformed into the one defined by P _B by successive pairwise anti-sorting between arbitrary pairs of elements. Symmetrically, the permutation defined by P _B can be transformed into the one defined by P _A by successive pairwise sorting (or, equivalently, by an application of a comparison network; see e.g. Knuth [39]).

Bruhat order is an important group-theoretic concept, which can be generalised to arbitrary Coxeter groups (see Björner and Brenti [9], Denton et al. [20] for more details and further references).

Many equivalent definitions of the Bruhat order on permutations are known; see e.g. [9, 22, 31, 36, 71] and references therein. A classical combinatorial characterisation of the Bruhat order, known as Ehresmann’s criterion or dot criterion, is as follows.

Theorem 6

We have P _A ⪯P _B , if and only if $P_{A}^{\varSigma}\leq P_{B}^{\varSigma}$ elementwise.

Proof

Straightforward from the definitions; see e.g. [9]. □

Example

We have

Note that the permutation matrix on the right can be obtained from the one on the left by anti-sorting the 2×2 submatrix at the intersection of the top two rows with the leftmost and rightmost columns.

We also have

The above two permutation matrices are incomparable in the Bruhat order.

Theorem 6 immediately gives one an algorithm for deciding whether two permutations are Bruhat-comparable in time O(n ²). To the author’s knowledge, no asymptotically faster algorithm for deciding Bruhat comparability has been known so far.

To demonstrate an application of our techniques, we now give a new characterisation of the Bruhat order in terms of the unit-Monge monoid (or, equivalently, the seaweed monoid). This characterisation will give us a substantially faster algorithm for deciding Bruhat comparability.

Intuitively, the connection between the Bruhat order and seaweeds is as follows. Consider matrix P _A and the rotated matrix $P_{A}^{R}$. The matrix rotation induces a one-to-one correspondence between the nonzeros of $P_{A}^{R}$ and P _A , and therefore also between individual seaweeds in their reduced seaweed braids. A pair of seaweeds cross in a reduced braid of $P_{A}^{R}$, if and only if the corresponding pair of seaweeds do not cross in a reduced braid of P _A . Now consider the product braid $P_{A}^{R} \boxdot P_{A}$, where each seaweed is made up of two mutually corresponding seaweeds from $P_{A}^{R}$ and P _A , respectively. Every pair of seaweeds in braid $P_{A}^{R} \boxdot P_{A}$ either cross in the top sub-braid $P_{A}^{R}$, or in the bottom sub-braid P _A , but not in both. Therefore, the product braid is a reduced seaweed braid, in which every pair of seaweeds cross exactly once. Thus, we have $P_{A}^{R} \boxdot P_{A} = \mathit{Id}^{R}$.

Now suppose P _A ⪯P _B . By Theorem 6, we have $P_{A}^{\varSigma}\leq P_{B}^{\varSigma}$ elementwise. Therefore, by Definition 7, $P_{A}^{R\varSigma} \odot P_{A}^{\varSigma}\leq P_{A}^{R\varSigma} \odot P_{B}^{\varSigma}$ elementwise, hence by Theorem 6, we have $P_{A}^{R} \boxdot P_{A} \preceq P_{A}^{R} \boxdot P_{B}$. However, as argued above, $P_{A}^{R} \boxdot P_{A} = \mathit{Id}^{R}$, which is the highest possible permutation matrix in the Bruhat order, corresponding to the reverse identity permutation. Therefore, $P_{A}^{R} \boxdot P_{B} = \mathit{Id}^{R}$. We thus have a necessary condition for P _A ⪯P _B . It turns out that this condition is also sufficient, giving us a new, computationally efficient criterion for Bruhat comparability.

Theorem 7

We have P _A ⪯P _B , if and only if $P_{A}^{R} \boxdot P_{B} = \mathit{Id}^{R}$.

Proof

Let i,j∈[0:n]. We have

$$\begin{aligned} &P_A^{R\varSigma}(i,j) + P_B^\varSigma(j,n-i) \quad\mbox{(definition of $R$)} \\ &\quad{}=\bigl(n-i - P_A^\varSigma(j,n-i)\bigr) + P_B^\varSigma(j,n-i) \quad\mbox{(term rearrangement)} \\ &\quad{}=\bigl(P_B^\varSigma(j,n-i) - P_A^\varSigma(j,n-i)\bigr) + n-i \end{aligned}$$

(15)

We now prove the implication separately in each direction.

Necessity.:

Let P _A ⪯P _B . By (15) and Theorem 6, we have

This lower bound is attained at j=0 (and, symmetrically, j=n): we have $P_{A}^{R\varSigma}(i,0) + P_{B}^{\varSigma}(0,n-i) = 0+(n-i) = n-i$. Therefore,

$$\begin{aligned} &\bigl(P_A^R \boxdot P_B \bigr)^\varSigma(i,n-i) \quad\mbox{(definition of $\boxdot$)} \\ &\quad{}=\min_j \bigl(P_A^{R\varSigma}(i,j) + P_B^\varSigma(j,n-i)\bigr) = n-i \quad\mbox{(attained at $j=0$)} \end{aligned}$$

It is now easy to prove (e.g. by induction on n) that $P_{A}^{R} \boxdot P_{B} = \mathit{Id}^{R}$ is the only permutation matrix satisfying the above equation for all i.

Sufficiency.:

Let $P_{A}^{R} \boxdot P_{B} = \mathit{Id}^{R}$. By Definition 7, we have

for all i. Therefore, for all i, j, $P_{A}^{R\varSigma}(i,j) + P_{B}^{\varSigma}(j,n-i) \geq n-i$. By (15), this is equivalent to $P_{B}^{\varSigma}(j,n-i) - P_{A}^{\varSigma}(j,n-i) \geq0$, therefore $P_{A}^{\varSigma}(j, n-i) \leq P_{B}^{\varSigma}(j, n-i)$, hence by Theorem 6, we have P _A ⪯P _B .  □

The combination of Theorems 5 and 7 gives us an algorithm for deciding Bruhat comparability of permutations in time O(nlogn).

4 Applications in String Comparison

The longest common subsequence (LCS) problem is a classical problem in computer science. Given two strings a, b of lengths m, n respectively, the LCS problem asks for the length of the longest string that is a subsequence of both a and b. This length is called the strings’ LCS score. The classical dynamic programming algorithm for the LCS problem [51, 68] runs in time O(mn); the best known algorithms improve on this running time by some (model-dependent) polylogarithmic factors [8, 17, 47, 70]. We refer the reader to monographs [18, 32] for the background on this problem and further references.

The semi-local LCS problem is a generalisation of the LCS problem, arising naturally in the context of string comparison. Given two strings a, b as before, the semi-local LCS problem asks for the LCS score of each string against all substrings of the other string, and of all prefixes of each string against all suffixes of the other string.

In [60, 61], we introduced the semi-local LCS problem, described its connections with unit-Monge matrices and seaweed braids, and gave a number of its algorithmic applications. Many of these applications use distance multiplication of simple unit-Monge matrices as a subroutine. In these cases, we can immediately obtain improved algorithms by plugging in the new multiplication algorithm given by Theorem 5. The rest of this section gives a few examples of such improvements. For further applications of our method, we refer the reader to [57].

4.1 Semi-Local LCS Between Permutations

An important special case of string comparison is where each of the input strings a, b is a permutation string, i.e. a string that consists of all distinct characters. Without loss of generality, we may assume that m=n, and that both strings are permutations of a given totally ordered alphabet of size n. The semi-local LCS problem on permutations is equivalent to finding the length of the longest increasing subsequence (LIS) in every substring of a given permutation string.

In [61], we gave an algorithm for the semi-local LCS problem on permutation strings, running in time O(n ^1.5). By using the algorithm of Theorem 5, the running time improves to O(nlog² n).

4.2 Cyclic LCS Between Permutations

The cyclic LCS problem on permutation strings is equivalent to the LIS problem on a circular string. This problem has been considered by Albert et al. [2], who gave a Monte Carlo randomised algorithm, running in time O(n ^1.5logn) with small error probability.

In [61], we gave an algorithm for the cyclic LCS problem on permutation strings, running in deterministic time O(n ^1.5). By using the algorithm of Theorem 5, the running time improves to O(nlog² n).

4.3 Maximum Clique in a Circle Graph

A circle graph [25, 29] is defined as the intersection graph of a set of chords in a circle, i.e. the graph where each node represents a chord, and two nodes are adjacent, whenever the corresponding chords intersect. We consider the maximum clique problem on a circle graph.

The interval model of a circle graph is obtained by cutting the circle at an arbitrary point and laying it out on a line, so that the chords become (closed) intervals. The original circle graph is isomorphic to the overlap graph of its interval model, i.e. the graph where each node represents an interval, and two nodes are adjacent, whenever the corresponding intervals intersect but do not contain one another.

Figure 4 shows an instance of the maximum clique problem on a six-node circle graph. Figure 4a shows the set of chords defining a circle graph, with one of the maximum cliques highlighted in bold red. The cut point is shown by scissors. Figure 4b shows the corresponding interval model; the dotted diagonal line contains the intervals, each defined by the diagonal of a square. The squares corresponding to the maximum clique are highlighted in bold red.

Fig. 4

A circle graph and its maximum clique

It has long been known that the maximum clique problem in a circle graph on n nodes is solvable in polynomial time [27]. A number of algorithms have been proposed for this problem [4, 35, 48, 55]; the problem has also been studied in the context of line arrangements in the hyperbolic plane [23, 37]. Given an interval model of a circle graph, the running time of the above algorithms is O(n ²) in the worst case, i.e. when the input graph is dense.

In [59, 61], we gave an algorithm running in time O(n ^1.5). By using the algorithm of Theorem 5, the running time improves to O(nlog² n).

4.4 Compressed String Comparison

String compression is a classical paradigm, touching on many different areas of computer science. From an algorithmic viewpoint, it is natural to ask whether compressed strings can be processed efficiently without decompression. Early examples of such algorithms were given e.g. by Amir et al. [3] and by Rytter [56].

We consider the following general model of compression. Let t be a string of length n (typically large). String t will be called a grammar-compressed string (GC-string), if it is generated by a context-free grammar, also called a straight-line program (SLP). An SLP of length $\bar{n}$, $\bar{n} \leq n$, is a sequence of $\bar{n}$ statements. A statement numbered k, $1 \leq k \leq\bar{n}$, has one of the following forms:

$$\begin{aligned} &t_k = \alpha \quad\text{where $\alpha$ is an alphabet character} \\ &t_k = t_i t_j \quad\text{where $1 \leq i,j < k$} \end{aligned}$$

We identify every symbol t _r with the string it expands to; in particular, we have $t = t_{\bar{n}}$. In general, the plain string length n can be exponential in the GC-string length $\bar{n}$.

As a special case, grammar compression includes the classical LZ78 and LZW compression schemes by Ziv, Lempel and Welch [69, 73]. It should also be noted that certain other compression methods, such as e.g. LZ77 [72] and run-length compression, do not fit directly into the grammar compression model.

The LCS problem on two GC-strings has been considered by Lifshits and Lohrey [45, 46], and proven to be PP-hard (and therefore NP-hard).

We consider the LCS problem between a plain (uncompressed) pattern string p of length m, and a grammar-compressed text string t of length n, generated by an SLP of length $\bar{n}$. In the special case of LZ77 or LZW compression of the text, the algorithm of Crochemore et al. [17] solves the LCS problem in time $O(m \bar{n})$. Thus, LZ77 or LZW compression of one of the input strings only slows down the LCS computation by a constant factor relative to the classical dynamic programming LCS algorithm, or by a polylogarithmic factor relative to the best known LCS algorithms.

The general case of an arbitrary GC-text appears more difficult. A GC-text is a special case of a context-free language, which consists of a single string. Therefore, the LCS problem between a GC-text and a plain pattern can be regarded as a special case of the edit distance problem between a context-free language given by a grammar of size $\bar{n}$, and a pattern string of size m. For this more general problem, Myers [50] gave an algorithm running in time $O(m^{3} \bar{n} + m^{2} \cdot\bar{n} \log\bar{n})$. In [62], we gave an algorithm for another generalisation of LCS problem between a GC-text and a plain pattern, running in time $O(m^{1.5} \bar{n})$. Lifshits [44] asked whether the LCS problem in the same setting can be solved in time $O(m \bar{n})$. Our new method gives an algorithm for the LCS problem between a GC-string and an uncompressed string running in time $O(m \log m \cdot\bar{n})$, thus approaching an answer to Lifshits’ question within a logarithmic factor.

Hermelin et al. [34] and Gawrychowski [28] refined the application of our techniques as follows. They consider the rational-weighted alignment problem (equivalently, the LCS or Levenshtein distance problems) on a pair of GC-strings a, b of total compressed length $\bar{r} = \bar{m} + \bar{n}$, parameterised by the strings’ total plain length r=m+n. The algorithm of [34] runs in time $O(r \log(r/\bar{r}) \cdot\bar{r})$, which is improved in [28] to $O(r \log^{1/2} (r/\bar{r}) \cdot\bar{r})$. In both cases, our algorithm of Theorem 5 is used as a subroutine.

5 Conclusion

In this work, we have given a fast algorithm for distance multiplication of simple unit-Monge matrices, running in time O(nlogn). The only known lower bound is trivial Ω(n). Therefore, Landau’s question whether the problem can be solved in time O(n) is still open, although we have now approached an answer within a logarithmic factor.

Our approach unifies and gives improved solutions to a number of algorithmic problems. It is likely that the scope of the applications can be widened still further, e.g. by considering new kinds of approximate matching and approximate repeat problems in strings.

The algebraic structure underlying our method is the distance-multiplication monoid of simple unit-Monge matrices, which we call the seaweed monoid. Traditionally, this structure is known as the 0-Hecke monoid of the symmetric group; it is a special case of a Coxeter monoid. Therefore, one may expect implications of our work in computational (semi)group theory. There are also potential connections with tropical mathematics, e.g. the tropical rank theory (see e.g. [21]).

In [40], we used distance multiplication of simple unit-Monge matrices to obtain the first parallel LCS algorithm with scalable communication. It would be interesting to see whether the fast distance multiplication algorithm given in the current work can be efficiently parallelised, and whether this can be used to achieve further improvement in the communication efficiency of parallel LCS computation.