Hardness of Approximation for Crossing Number

Abstract

We show that, if $\mathrm{P}\not=\mathrm{NP}$, there is a constant c ₀>1 such that there is no c ₀-approximation algorithm for the crossing number, even when restricted to 3-regular graphs.

1 Introduction

A drawing of a graph G is a mapping $\mathcal {D}$ associating a point $\mathcal {D}(v)\in \mathbb{R}^{2}$ to each vertex v∈V(G) and a simple, polygonal path $\mathcal {D}(e)$ to each edge e∈E(G) with the following properties:

• for any two distinct vertices u,v∈V(G), $\mathcal {D}(u)\not= \mathcal {D}(v)$;

• for every edge uv∈E(G), the endpoints of the path $\mathcal {D}(uv)$ are $\mathcal {D}(u)$ and $\mathcal {D}(v)$;

• for every edge e∈E(G) and every vertex u∈V(G), the (relative) interior of the path $\mathcal {D}(e)$ is disjoint from $\mathcal {D}(u)$.

A crossing in a drawing $\mathcal {D}$ of a graph G is a pair ({e,e′},p), where e and e′ are distinct edges of G, and p∈ℝ² is a point that belongs to the interior of the paths $\mathcal {D}(e)$ and $\mathcal {D}(e')$. The number of crossings of a drawing $\mathcal {D}$ is denoted by $\hbox {\texttt {cr}}(\mathcal {D})$ and is called the crossing number of the drawing. The crossing number cr(G) of a graph G is the minimum $\hbox {\texttt {cr}}(\mathcal {D})$ taken over all drawings $\mathcal {D}$ of G. A drawing without crossings is an embedding.

Garey and Johnson [10] showed that the following optimization problem is NP-hard.

CrossingNumber

Instance: A graph G.

Feasible solutions: Drawings of G.

Measure: Crossing number of the drawing.

Goal: Minimization.

This result has been extended in several directions. Hliněný [12] proved that the problem remains NP-hard for cubic graphs (3-regular graphs). This was reproved using crossing numbers with rotation systems by Pelsmajer et al. [16]. In a recent paper with Mohar [4] we have shown that computing the crossing number for near-planar graphs is NP-hard. A graph is near-planar if it is obtained from a planar graph by adding one edge.

None of the these proofs implies inapproximability of CrossingNumber under the assumption that $\mathrm{P}\not=\mathrm{NP}$. However, under stronger assumptions, inapproximability can be obtained from known results. More precisely, the NP-hardness proof of Garey and Johnson [10] is from LinearArrangement, and it implies that any inapproximability result for LinearArrangement carries into an inapproximability result for CrossingNumber. Ambühl et al. [1] have recently shown that there is no polynomial-time approximation scheme (PTAS) for LinearArrangement, unless NP-complete problems can be solved in randomized subexponential time. (The precise assumption is that Satisfiability cannot be solved in probabilistic time $2^{n^{\epsilon}}$ for any constant ϵ>0.) This directly implies that there is no PTAS for CrossingNumber, unless NP-complete problems can be solved in randomized subexponential time. Although the NP-hardness proofs for cubic graphs by Hliněný [12] and Pelsmajer et al. [16] also use reductions from LinearArrangement, they do not imply any inapproximability because the value of the optimal linear arrangement is a lower-order term in the crossing number of the graphs constructed in the reduction.

In this paper we show that, if $\mathrm{P}\not=\mathrm{NP}$, there is some constant c ₀>1 such that there is no c ₀-approximation for CrossingNumber. The result holds also for cubic graphs. Therefore, we strengthen the result mentioned in the previous paragraph by weakening the hypothesis. Moreover, our reduction also implies inapproximability for cubic graphs, which was not known before under any assumption. We also provide a conceptually new proof of NP-hardness because we reduce from MultiwayCut. As noted by Hliněný [12], for cubic graphs, the minor crossing number is equal to the crossing number. Thus, we also obtain inapproximability results for the minor crossing number.

On the positive side, the best approximation algorithm for CrossingNumber, by Chuzhoy [6], has an approximation factor of $O(n^{9/10}\operatorname{poly}(\Delta \log n))$ for graphs with n vertices and maximum degree Δ. It is worth noting that computing the crossing number is fixed-parameter tractable with respect to the crossing number itself [11, 14]. Research on crossing number has been very active. Vrt’o [17] lists over 600 references.

2 Preliminaries

Edge Weights

Our construction will be easier to describe if we work with weighted edges. The weights will always be positive integers. Assume that G is an edge-weighted graph where the weight of each edge e is denoted by w _e ∈ℕ. The intuition is that w _e tells how many parallel edges are represented by e. The crossing number of a drawing for such an edge-weighted graph is defined by taking the sum of w _e ⋅w _e′, over all crossings ({e,e′},p) of the drawing. Again, the crossing number of such an edge-weighted graph is defined as the minimum of the crossing numbers over all drawings.

Let G be an edge-weighted graph. We can construct an unweighted graph ϕ(G) from G by replacing each edge uv∈E(G) with a family P _uv of w _e parallel paths of length 2 that connect u to v. It is easy to see that cr(G)=cr(ϕ(G)). Indeed, any drawing $\mathcal {D}_{G}$ of G gives rise to a drawing $\mathcal {D}_{\phi(G)}$ of ϕ(G) with $\hbox {\texttt {cr}}(\mathcal {D}_{\phi(G)})=\hbox {\texttt {cr}}(\mathcal {D}_{G})$ by drawing each family P _e within a small neighborhood of $\mathcal {D}_{G}(e)$. On the other hand, any drawing $\mathcal {D}_{\phi(G)}$ of ϕ(G) can be used to construct a drawing $\mathcal {D}_{G}$ of G with $\hbox {\texttt {cr}}(\mathcal {D}_{G})\le \hbox {\texttt {cr}}(\mathcal {D}_{\phi(G)})$ by drawing each edge e∈E(G) along the path of P _e that participates in fewer crossings.

When the weights w _e ∈ℕ, e∈E(G), are all bounded by a polynomial in |V(G)|, then the graph ϕ(G) can be constructed from G in polynomial time.

Rotation Systems

A rotation system in a graph G is a list π=(π _v ) _v∈V(G), where each π _v is a cyclic ordering of the edges of G incident to v. A drawing $\mathcal {D}$ of a graph G agrees with the rotation system π if, for each vertex v∈V(G), the clockwise ordering around $\mathcal {D}(v)$ of the drawings of the edges incident to v is the same as the cyclic ordering π _v . For a graph G and a rotation system π in G, we define cr(G,π) as the minimum of the crossing numbers over all drawings of G that agree with π. This concept can easily be extended to edge-weighted graphs.

If G is an edge-weighted graph and π is a rotation system in G, we can define a rotation system ϕ _π (G,π) in ϕ(G): for each edge uv∈E(G), we replace in π _u the edge uv by the edges of P _uv incident to u in such a way that the cyclic ordering of the paths in P _uv are opposite at u and v. This implies that the paths of P _uv can be drawn without crossings among themselves. The same argument that was used above shows that cr(G,π)=cr(ϕ(G),ϕ _π (G,π)). The rotation ϕ _π (G,π) can be computed in polynomial time, provided that the edge-weights of G are bounded by a polynomial in |V(G)|.

A combinatorial embedding of a graph G is a rotation system π such that some embedding $\mathcal {D}$ of G agrees with π. Whitney’s theorem states that a 3-connected, planar graph has a unique combinatorial embedding [9, Chap. 4].

Consider any graph G and any rotation system π in G. In an optimal drawing of G that agrees with π, each pair of edges participates in at most one crossing. Indeed, if the edges e and e′ would participate in two crossings ({e,e′},p) and ({e,e′},p′), we could obtain another drawing with fewer crossings: we exchange the portions of D(e) and D(e′) between p and p′ and then perturb the drawing around p and p′ slightly to avoid the intersection. In particular, for any rotation system π of the complete graph K _t , we have cr(K _t ,π)≤t ⁴.

Multiway Cut

Our reduction will be from the following optimization problem about connectivity:

MultiwayCut

Instance: A pair (G,T) where G is a connected graph and T⊂V(G).

Feasible solutions: Sets of edges F⊆E(G) such that, for each distinct t,t′∈T, there is no path in G−F connecting t to t′.

Measure: Cardinality of F.

Goal: Minimization.

The set T is the set of terminals. Dahlhaus et al. [8] proved that MultiwayCut is MAX SNP-hard even when restricted to instances with 3 terminals.¹ This implies that there is a constant c _M >1 such that there is no c _M -approximation algorithm for MultiwayCut with 3 terminals, unless $\mathrm{P}\not=\mathrm{NP}$. (In particular, the problem is APX-hard for 3 terminals; see [2].) We will only use instances (G,T) of MultiwayCut with |T|=3. We denote by mwc(G,T) the size of an optimal solution for (G,T).

Notation

We use [3]={1,2,3}, and, for the rest of the paper, the indices depending on i are always taken modulo 3.

3 From Multiway Cut to Crossing Number

Let A be the graph defined by

The graph A is shown in Fig. 1, where it is clear that A is planar. Furthermore, it is a subdivision of a 3-connected graph, and thus it has a unique combinatorial embedding.

Fig. 1

The graph A

Consider any instance (G,T) to MultiwayCut with |T|=3. We will use n=|V(G)| and n ² as a rough upper bound to |E(G)|. We construct an edge-weighted graph H=H(G,T) as follows:

• (i) Construct A and assign weight n ⁵ to its edges.

• (ii) Construct the graph H′=G∪A, where the edges of G have weight 1.

• (iii) We identify each vertex of T with a distinct vertex x _i of A. That is, if T={t ₁,t ₂,t ₃}, then, for each i∈[3], identify x _i and t _i .

This finishes the construction of H. See Fig. 2 for an example. Let π be any rotation system for H such that:

• the restriction of π to A is the unique combinatorial embedding of A.

• for each i∈[3], the edges x _i a _i−1 and x _i a _i+1 are consecutive in the cyclic ordering $\pi_{x_{i}}$. That is, any edge of H−E(A) incident to x _i is between x _i a _i+1 and x _i a _i−1 in the rotation system $\pi_{x_{i}}$.

Fig. 2

Left: a graph G with vertices T={t ₁,t ₂,t ₃} marked with filled-in squares. Right: the corresponding graph H=H(G,T). Thicker edges have weight n ⁵=30⁵, and the other edges have weight 1. The rotation system of the drawing is a possible π

In the next two lemmas we obtain bounds relating cr(H) and cr(H,π) to mwc(G,T). Our bounds are not tight, but this does not affect our eventual results.

Lemma 1

We have

$$\hbox {\texttt {cr}}(H,\pi) \le n^5\cdot \hbox {\texttt {mwc}}(G,T) + 3 n^4. $$

Proof

Let F be an optimal solution to MultiwayCut for (G,T). Thus, we have |F|=mwc(G,T). For each i∈[3], let G _i be the connected component of G−F that contains x _i . By the optimality of F, we have G=(⋃ _i∈[3] G _i )+F. Indeed, if there would be another connected component, any edge of F connecting that component to any other connected component could be removed from F and obtain a better solution.

We construct a drawing $\mathcal {D}$ of H as follows. Firstly, take an embedding A without any crossings; such embedding is shown in Fig. 1. Then, for each i∈[3], draw the component of G _i inside the region limited by x _i a _i−1 a ₄ a _i+1 x _i respecting the rotation system π and with the minimum number of crossings. Finally, draw each edge of F optimally in the current drawing. In such drawing, an edge connecting G _i to G _j will be drawn crossing the edge a ₄ a _k , where $k\not= i,j$. See Fig. 3 for a sketch. Let $\mathcal {D}$ be the resulting drawing.

Fig. 3

Sketch of the drawing in Lemma 1. The dashed arcs represent edges of F

We now bound the number of crossings in the drawing $\mathcal {D}$. The restriction $\mathcal {D}(A)$ has no crossings by construction. For each i∈[3], the restriction $\mathcal {D}(G_{i})$ has at most |V(G _i )|⁴ crossings because, as mentioned in Sect. 2, for any rotation system π′ of the complete graph K _t , we have cr(K _t ,π′)≤t ⁴. Each single edge of F can be drawn with n ⁵+2n ² crossings. Indeed, if v _i v _j ∈F connects G _i to G _j and we denote by k the element of [3]∖{i,j}, there is an arc from v _i to any point on $\mathcal {D}(a_{4} a_{k})$ that crosses at most |E(G _i )|+|F| edges, and there is an arc connecting any point in $\mathcal {D}(a_{4} a_{k})$ to v _j with at most |E(G _j )|+|F| crossings. The described drawing of v _i v _j has, using a very rough estimate,

$$\bigl( \big|E(G_i)\big|+|F| \bigr) + n^5+ \bigl( \big|E(G_j)\big|+|F| \bigr) \le n^5 + 2 \big|E(G)\big| \le n^5 + 2 n^2 $$

crossings. We conclude that

 □

The following result is independent of rotation systems.

Lemma 2

From any drawing $\mathcal {D}$ of H we can obtain a feasible solution F to MultiwayCut(G,T) such that $|F|\le \hbox {\texttt {cr}}(\mathcal {D}) /n^{5}$ in time that is polynomial in the size of the description of  $\mathcal {D}$. In particular,

$$n^5\cdot \hbox {\texttt {mwc}}(G,T) \le \hbox {\texttt {cr}}(H). $$

Proof

Consider any drawing $\mathcal {D}$ of H. We can compute $\hbox {\texttt {cr}}(\mathcal {D})$ in time that is polynomial in the size of the description of $\mathcal {D}$. If $\hbox {\texttt {cr}}(\mathcal {D})$ is larger than n ⁷, we can just take F=E(G) because it satisfies $|F|\le n^{2}\le \hbox {\texttt {cr}}(\mathcal {D})/n^{5}$. If $\hbox {\texttt {cr}}(\mathcal {D})$ is smaller than n ⁷, we proceed as follows. The restriction of $\mathcal {D}$ to A is an embedding because each edge of A has weight n ⁵. For each i∈[3], let C _i denote the cycle a ₄ a _i−1 b _i−1 b _i+1 a _i+1 a ₄. In the embedding $\mathcal {D}(A)$ the cycle C _i separates x _i =t _i from x _j =t _j whenever $i\not= j$.

Define the set of edges

$$F = \bigl\{ e\in E(G)\mid \mathcal {D}(e)\ \mbox{intersects}\ \mathcal {D}(C_1), \mathcal {D}(C_2)\ \mbox{or}\ \mathcal {D}(C_3)\bigr\}. $$

Note that F can be computed in polynomial time from $\mathcal {D}$. Since each edge of F crosses (at least once) some edge of A, we have

$$\hbox {\texttt {cr}}(\mathcal {D}) \ge n^5 \cdot |F|. $$

Furthermore, F is a feasible solution to MultiwayCut for (G,T) because, for each path P in G that connects t _i to t _j , $i\not= j$, the drawing $\mathcal {D}(P)$ has to cross the cycle $\mathcal {D}(C_{i})$ and thus P has an edge in F.

The bound n ⁵⋅mwc(G,T)≤cr(H) is obtained by considering an optimal drawing $\mathcal {D}^{*}$ of H. Such a drawing $\mathcal {D}^{*}$ gives a feasible solution F that satisfies

$$n^5\cdot \hbox {\texttt {mwc}}(G,T) \le n^5\cdot |F| \le \hbox {\texttt {cr}}\bigl(\mathcal {D}^* \bigr) = \hbox {\texttt {cr}}(H). $$

The result follows. □

We next explain how to construct a cubic graph $\tilde{H}=\tilde{H}(G,T)$ such that

$$n^5\cdot \hbox {\texttt {mwc}}(G,T) \le \hbox {\texttt {cr}}(\tilde{H}) \le n^5\cdot \hbox {\texttt {mwc}}(G,T) + 3 n^4. $$

The idea is a straightforward adaptation of the technique used by Pelsmajer et al. [16]; we include the details for the sake of completeness.

In a first step, we construct the unweighted graph H′=ϕ(H) and the rotation system π′=ϕ _π (H(G,T),π) in H′, as described in Sect. 2. It holds that cr(H′)=cr(H) and cr(H′,π′)=cr(H,π).

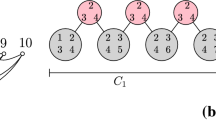
In a second step, we replace each vertex v∈H′ by a cubic grid $\mathcal{C}_{v}$ of width deg _H′(v) and height 8n ⁷; see Fig. 4. (The cubic grid of width d and height h is obtained from a regular, rectangular grid of width 2d and height h where the vertical edge connecting (i,j) to (i,j+1) is removed whenever i+j is odd.) If $e^{v}_{1},\dots,e^{v}_{\deg_{H'}(v)}$ are the edges incident to v in H′ ordered as in the cyclic ordering $\pi'_{v}$, then we attach the edges $e^{v}_{1},\dots,e^{v}_{\deg_{H'}(v)}$ to the degree-two consecutive vertices of the cubic grid $\mathcal{C}_{v}$ that are on the higher row. Finally, we make the graph cubic by removing vertices of degree 1 and contracting some edges incident to vertices of degree 2. This finishes the construction of $\tilde{H}=\tilde{H}(G,T)$. Note that the construction of $\tilde{H}$ can be made in polynomial time because the weight of each edge of H is bounded by n ⁵.

Fig. 4

The solid edges form a cubic grid of width 6 and height 6. The dashed edges show how the edges $e^{v}_{1},e^{v}_{2},\dots$ get attached to $\mathcal{C}_{v}$

Lemma 3

We have

$$n^5\cdot \hbox {\texttt {mwc}}(G,T) \le \hbox {\texttt {cr}}(\tilde{H}) \le n^5\cdot \hbox {\texttt {mwc}}(G,T) + 3 n^4. $$

Furthermore, from any drawing $\tilde{\mathcal {D}}$ of $\tilde{H}$ we can obtain a feasible solution F to MultiwayCut(G,T) such that $|F|\le \hbox {\texttt {cr}}(\tilde{\mathcal {D}}) /n^{5}$ in time that is polynomial in the size of the description of $\tilde{\mathcal {D}}$.

Proof

It is clear that any drawing $\mathcal {D}'$ of H′ with rotation system π′ can be converted into a drawing of $\tilde{H}$ by a local replacement around $\mathcal {D}'(v)$, for each v∈V(H′), without introducing additional crossings. Therefore,

$$\hbox {\texttt {cr}}(\tilde{H}) \le \hbox {\texttt {cr}}\bigl(H',\pi'\bigr) = \hbox {\texttt {cr}}(H, \pi) \le n^5\cdot \hbox {\texttt {mwc}}(G,T) + 3 n^4 $$

because of Lemma 1.

To see the other inequality, consider an optimal drawing $\tilde{\mathcal {D}}$ of $\tilde{H}$. The first part of the proof implies that $\hbox {\texttt {cr}}(\tilde{\mathcal {D}})<4n^{7}$. Therefore, in each cubic grid $\mathcal{C}_{v}$, v∈V(H′), there is at least one horizontal row, let us call it R _v , that does not participate in any crossing of $\tilde{\mathcal {D}}$. For each vertex v∈V(H′), there are deg _H′(v) vertex-disjoint paths $P^{v}_{i}$ in $\mathcal{C}_{v}$, i=1,…,deg _H′(v), connecting the endvertex of $e^{v}_{i}$ to a vertex of R _v . We contract the row R _v to a point and remove from the drawing all the edges of $\mathcal{C}_{v}$, but those participating in the paths $P^{v}_{1},\dots, P^{v}_{\deg_{H'}(v)}$. Repeating this for each vertex v∈V(H′), we obtain a drawing $\mathcal {D}'$ of a subdivision of H′ with at most $\hbox {\texttt {cr}}(\tilde{\mathcal {D}})$ crossings. This implies that $\hbox {\texttt {cr}}(H)=\hbox {\texttt {cr}}(H') \le \hbox {\texttt {cr}}(\tilde{D}) = \hbox {\texttt {cr}}(\tilde{H})$. By Lemma 2 it follows that

$$\hbox {\texttt {cr}}(\tilde{H}) \ge \hbox {\texttt {cr}}(H) \ge n^5\cdot \hbox {\texttt {mwc}}(G,T). $$

To obtain from a drawing $\tilde{\mathcal {D}}$ of $\tilde{H}$ a feasible solution F with $|F|\le \hbox {\texttt {cr}}(\tilde{\mathcal {D}}) /n^{5}$, we proceed as follows. We compute $\hbox {\texttt {cr}}(\tilde{\mathcal {D}})$ in time that is polynomial in the size of the description of $\tilde{\mathcal {D}}$. If $\hbox {\texttt {cr}}(\tilde{\mathcal {D}})\ge n^{7}$, we just return F=E(G). Otherwise we construct the drawing $\mathcal {D}'$ of H′ from $\tilde{\mathcal {D}}$, as described above. As discussed in Sect. 2, from the drawing $\mathcal {D}'$ of H′=ϕ(H) we can obtain a drawing $\mathcal {D}$ of H with $\hbox {\texttt {cr}}(\mathcal {D})\le \hbox {\texttt {cr}}(\mathcal {D}')$. Finally, from the drawing $\mathcal {D}$ of H we can use Lemma 2 to extract a feasible solution F to MultiwayCut(G,T) such that

$$|F|\le \hbox {\texttt {cr}}(\mathcal {D}) /n^5 \le \hbox {\texttt {cr}}\bigl(\mathcal {D}' \bigr)/n^5 \le \hbox {\texttt {cr}}(\tilde{\mathcal {D}}). $$

Since all the steps can be carried out in polynomial time, the result follows. □

Theorem 4

There is a constant c ₀>1 such that, if $\mathrm{P}\not=\mathrm{NP}$, there is no c ₀-approximation algorithm for CrossingNumber, even when restricted to cubic graphs.

Proof

Let c _M >1 be a constant such that it is NP-hard to compute a c _M -approximation to MultiwayCut when |T|=3. (See the discussion in Sect. 2.) Take c ₀=c _M −ε for an arbitrary constant ε with 0<ε<c _M −1. We will see that it is NP-hard finding a c ₀-approximation to CrossingNumber in cubic graphs.

Assume, for the sake of contradiction, that there is a c ₀-approximation algorithm for CrossingNumber in cubic graphs. We can then obtain a c _M -approximation to MultiwayCut(G,T) in polynomial time as follows. Let n=|V(G)|. If n is smaller than 3c ₀/ε, which is a constant, we run any brute force algorithm. Otherwise, we construct in polynomial time the cubic graph $\tilde{H}=\tilde{H}(G,T)$, as described above, use the c ₀-approximation algorithm to compute a drawing $\tilde{\mathcal {D}}$ of $\tilde{H}$ with $\hbox {\texttt {cr}}(\tilde{\mathcal {D}})\le c_{0}\cdot \hbox {\texttt {cr}}(\tilde{H})$, use Lemma 3 to find a feasible solution F to MultiwayCut(G,T), and return F. We next argue that this algorithm is a c _M -approximation algorithm for MultiwayCut.

Because of Lemma 3, F is a feasible solution with $|F|\le \hbox {\texttt {cr}}(\tilde{\mathcal {D}}) /n^{5}$. On the other hand, $\hbox {\texttt {cr}}(\tilde{\mathcal {D}}) \le c_{0}\cdot \hbox {\texttt {cr}}(\tilde{H})$ because $\mathcal {D}$ is a c ₀-approximation to $\hbox {\texttt {cr}}(\tilde{H})$. Using Lemma 3, we obtain

Thus, returning F, we obtain a c _M -approximation to mwc(G,T), which is not possible unless $\mathrm{P}\not=\mathrm{NP}$. □

Bokal et al. [3] introduced the concept of minor crossing number. Hliněný [12] noted that for cubic graphs, the crossing number and the minor crossing number have the same value. We thus obtain the following.

Corollary 5

There is a constant c ₀>1 such that, if $\mathrm{P}\not=\mathrm{NP}$, there is no c ₀-approximation algorithm for the minor crossing number.

4 Conclusions

Since there are constant-factor approximation algorithms for MultiwayCut, a more careful reduction from MultiwayCut will not bring us beyond hardness of constant-factor approximations. Nevertheless, it seems hard to believe that there is an O(1)-approximation algorithm for CrossingNumber. As mentioned in the introduction, the currently best approximation factor is roughly O(n ^9/10).

A natural approach to improve the inapproximability result would be to reduce from a problem that is known to be harder. The problems 0-extension and MetricLabeling are generalizations of MultiwayCut, and stronger inapproximability results are known [7, 13, 15]. However, we have not been able to obtain fruitful reductions from those problems to CrossingNumber.

It remains a tantalizing open problem whether CrossingNumber can be solved in polynomial time for graphs with bounded treewidth. An obstacle is that we do not know whether LinearArrangement is NP-hard for graphs of bounded treewidth. If that were the case, then the reduction of Garey and Johnson [10] would increase the treewidth by a constant. On the other hand, MultiwayCut is solvable in polynomial-time for graphs of bounded treewidth: Chopra and Rao [5] discuss treewidth 2, and Dahlhaus et al. [8] note that it works for any bounded treewidth. Thus, the approach of this paper cannot lead to an NP-hardness proof of CrossingNumber for graphs of bounded treewidth.