Characterizing the Universal Rigidity of Generic Frameworks

Abstract

A framework is a graph and a map from its vertices to ${\mathbb E}^d$ (for some $d$). A framework is universally rigid if any framework in any dimension with the same graph and edge lengths is a Euclidean image of it. We show that a generic universally rigid framework has a positive semi-definite stress matrix of maximal rank. Connelly showed that the existence of such a positive semi-definite stress matrix is sufficient for universal rigidity, so this provides a characterization of universal rigidity for generic frameworks. We also extend our argument to give a new result on the genericity of strict complementarity in semidefinite programming.

1 Introduction

In this paper we characterize generic frameworks which are universally rigid in $d$-dimensional Euclidean space. A framework is universally rigid if, modulo Euclidean transforms, there is no other framework of the same graph in any dimension that has the same edge lengths. A series of papers by Connelly [8–10] and later Alfakih [2, 3] described a sufficient condition for a generic framework to be universally rigid. In this paper we show that this is also a necessary condition.

Universally rigid frameworks are especially relevant when applying semidefinite programming techniques to graph embedding problems. Suppose some vertices are embedded in ${\mathbb E}^d$ and we are told the distances between some of the pairs of vertices. The graph embedding problem is to compute the embedding (up to an unknown Euclidean transformation) from the data. This problem is computationally difficult as the graph embeddablity question is in general NP-HARD [27], but because of its utility, many heuristics have been attempted. One approach is to use semidefinite programming to find an embedding [20], but such methods are not able to find the solutions that are specifically $d$-dimensional, rather than embedded in some larger dimensional space. However, when the underlying framework is, in fact, universally rigid, then the distance data itself automatically constrains the dimension, and therefore the correct answer will be (approximately) found by the semidefinite program. The connection between rigidity and semi-definite programming was first explored by So and Ye [30].

We also discuss the more general topic of strict complementarity in semidefinite programming. Strict complementarity is a strong form of duality that is needed for the fast convergence of many interior point optimization algorithms. Using our arguments from universal rigidity, we show that if the semidefinite program has a sufficiently generic primal solution, then it must satisfy strict complementarity. This is in distinction with previous results on strict complementarity [1, 24] that require the actual parameters of the program to be generic. In particular, our result applies to programs where the solution is of a lower rank than would be found generically.

1.1 Rigidity Definitions

Definition 1.1

A graph $\Gamma$ is a set of $v$ vertices ${\mathcal V}(\Gamma )$ and $e$ edges ${\mathcal E}(\Gamma )$, where ${\mathcal E}(\Gamma )$ is a set of two-element subsets of ${\mathcal V}(\Gamma )$. We will typically drop the graph $\Gamma$ from this notation. A configuration $p$ is a mapping from ${\mathcal V}$ to ${\mathbb E}^v$. Let $C({\mathcal V})$ be the space of configurations. For $p\in C({\mathcal V})$ and $u \in {\mathcal V}$, let $p(u)$ denote the image of $u$ under $p$. Let $C^d({\mathcal V})$ denote the space of configurations that lie entirely in the ${\mathbb E}^d$, contained as the first $d$ dimensions of ${\mathbb E}^v$. A framework $(p,\Gamma )$ is the pair of a graph and a configuration of its vertices. For a given graph $\Gamma$ the length-squared function $\ell _\Gamma :C({\mathcal V})\rightarrow {\mathbb R}^e$ is the function assigning to each edge of $\Gamma$ its squared edge length in the framework. That is, the component of $\ell _\Gamma (p)$ in the direction of an edge $\{u,w\}$ is ${|p(u)-p(w) |}^2$.

Definition 1.2

A configuration in $C^d({\mathcal V})$ is proper if it does not lie in any affine subspace of ${\mathbb E}^d$ of dimension less than $d$. It is generic if its first $d$ coordinates (i.e., the coordinates not constrained to be $0$) do not satisfy any algebraic equation with rational coefficients.

Remark 1.3

A generic configuration in $C^d({\mathcal V})$ with at least $d+1$ vertices is proper.

Definition 1.4

The configurations $p, q$ in $C({\mathcal V})$ are congruent if they are related by an element of the group of ${{\mathrm{Eucl}}}(v)$ of rigid motions of ${\mathbb E}^v$.

A framework $(p,\Gamma )$ with $p\in C^d({\mathcal V})$ is universally rigid if any other configuration in $C({\mathcal V})$ with the same edge lengths under $\ell _{\Gamma }$ is a configuration congruent to $p$.

A graph $\Gamma$ is generically universally rigid in ${\mathbb E}^d$ if any generic framework $(p,\Gamma )$ with $p\in C^d({\mathcal V})$ is universally rigid.

Essentially, universal rigidity means that the lengths of the edges of $p$ are consistent with essentially only one embedding of $\Gamma$ in any dimension, up to $v$. (In general, a configuration in any higher dimension can be related by a rigid motion to a configuration in ${\mathbb E}^v$.) This is stronger than global rigidity, where the lengths fully determine the embedding in the smaller space ${\mathbb E}^d$. And global rigidity is, in turn, stronger than (local) rigidity, which only rules out continuous flexes in ${\mathbb E}^d$ that preserve edge lengths.

Remark 1.5

Universal rigidity or closely related notions have also been called dimensional rigidity [2], uniquely localizable [30], and super stability [9].

Remark 1.6

In Definition 1.4, it would be equivalent to require that $(p,\Gamma )$ be (locally) rigid in ${\mathbb E}^v$ since by a result of Bezdek and Connelly [6] any two frameworks with the same edge lengths can be connected by a smooth path in a sufficiently large dimension.

Remark 1.7

Universal rigidity, unlike local and global rigidity, is not a generic property of a graph: for many graphs, some generic frameworks are universally rigid and others are not. For instance, an embedding of a 4-cycle in the line ${\mathbb E}^1$ is universally rigid iff one side is long in the sense that its length is equal to the sum of the lengths of the others. On the other hand, some graphs, such as a simplex, and any trilateration graph [14] are generically universally rigid in ${\mathbb E}^d$. (A $d$-trilateration graph has the property that one can order its vertices such that the following holds: the first $d+2$ vertices are part of a simplex in $\Gamma$ and each subsequent vertex is adjacent in $\Gamma$ to $d+1$ previous vertices.) We do not know a characterization of generically universally rigid graphs.

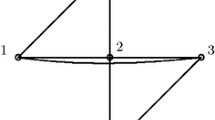
See Fig. 1 for examples of embedded graphs with increasing types of rigidity.

Fig. 1

Planar graph embeddings with increasing types of rigidity. From left to right, generically locally flexible graph, generically locally rigid graph, generically globally rigid graph, generic universally rigid framework, generically universally rigid graph. (More precisely, the fourth framework is not itself generic, but it and any generic framework close to it are universally rigid.) This paper focuses on frameworks of the type of the fourth one. The fifth graph is generically universally rigid as it is a 2-trilateration graph

1.2 Equilibrium Stresses

Definition 1.8

An equilibrium stress matrix of a framework $(p,\Gamma )$ is a matrix $\Omega$ indexed by ${\mathcal V}\times {\mathcal V}$ so that

• (1) for all $u,w \in {\mathcal V}$, $\Omega (u,w) = \Omega (w,u)$;

• (2) for all $u,w \in {\mathcal V}$ with $u \ne w$ and $\{u,w\} \not \in {\mathcal E}$, $\Omega (u,w) = 0$;

• (3) for all $u \in {\mathcal V}$, $\sum _{w\in {\mathcal V}} \Omega (u,w) = 0$; and

• (4) for all $u \in {\mathcal V}$, $\sum _{w\in {\mathcal V}} \Omega (u,w)p(w) = 0$.

(The last condition is the equilibrium condition.) Let $S_\Gamma (p)$ be the linear space of equilibrium stress matrices for $(p,\Gamma )$.

Conditions (3) and (4) give us:

$$\begin{aligned} \forall u \in {\mathcal V}\;\; \sum _{\{w \in {\mathcal V}\mid \{u,w\} \in {\mathcal E}\}}\!\!\Omega (u,w)(p(w) - p(u)) = 0. \end{aligned}$$

(1.1)

The kernel of an equilibrium stress matrix $\Omega$ of a framework $(p,\Gamma )$ always contains the subspace of ${\mathbb R}^v$ spanned by the coordinates of $p$ along each axis and the vector ${\mathbf {\vec {1}}}$ of all $1$’s. This corresponds to the fact that any affine image of $p$ satisfies all of the equilibrium stresses in $S_\Gamma (p)$. If $p$ is a proper $d$-dimensional configuration, these kernel vectors span a $(d+1)$-dimensional space, so for such frameworks ${{\mathrm{rank}}}\Omega \le v-d-1$.

Definition 1.9

We say that the edge directions of $(p,\Gamma )$ with $p\in C^d({\mathcal V})$ are on a conic at infinity if there exists a symmetric $d$-by-$d$ matrix $Q$ such that for all edges $(u,v)$ of $\Gamma$, we have

$$\begin{aligned}{}[p(u)-p(v)]^t Q [p(u)-p(v)] = 0, \end{aligned}$$

where the square brackets mean the projection of a vector in ${\mathbb E}^v$ to ${\mathbb E}^d$ (i.e., dropping the $0$’s at the end of $p(u)$).

Remark 1.10

If the edges of $(p,\Gamma )$ are not on a conic at infinity in $C^d({\mathcal V})$, then in particular $p$ is proper.

A framework has edges on a conic at infinity iff there is a continuous family of $d$-dimensional non-orthonormal affine transforms that preserve all of the edge lengths. However, if the configuration is not proper, this family of affine transforms might all be congruent to the original one.

1.3 Results

Connelly in a series of papers has studied the relationship between various forms of rigidity and equilibrium stress matrices. In particular he proved the following theorem that gives a sufficient condition for a framework to be universally rigid.

Theorem 1.11

(Connelly) Suppose that $\Gamma$ is a graph with $d+2$ or more vertices and $p$ is a (generic or not) configuration in $C^d({\mathcal V})$. Suppose that there is an equilibrium stress matrix $\Omega \in S_\Gamma (p)$ that is positive semidefinite (PSD) and that ${{\mathrm{rank}}}\Omega = v-d-1$. Also suppose that the edge directions of $p$ do not lie on a conic at infinity. Then $(p,\Gamma )$ is universally rigid.

Connelly also proved a lemma that allows him to ignore the conic at infinity issue when $p$ is generic.

Lemma 1.12

(Connelly) Suppose that $\Gamma$ is a graph with $d+2$ or more vertices and $p$ is a generic configuration in $C^d({\mathcal V})$. Suppose that there is an equilibrium stress matrix $\Omega \in S_\Gamma (p)$ with rank $v-d-1$. Then the edge directions of $p$ do not lie on a conic at infinity.

Putting these together, we can summarize this as

Corollary 1.13

Suppose that $\Gamma$ is a graph with $d+2$ or more vertices and $p$ is a generic configuration in $C^d({\mathcal V})$. Suppose that there is a PSD equilibrium stress matrix $\Omega \in S_\Gamma (p)$ with ${{\mathrm{rank}}}\Omega = v-d-1$. Then $(p,\Gamma )$ is universally rigid.

The basic ideas for the proof of Theorem 1.11 appear in [8] where they were applied to show the universal rigidity of Cauchy polygons. It is also described in [9] and stated precisely in [10, Theorem 2.6]. Lemma 1.12 can be derived from the proof of Theorem 1.3 in [11]. Corollary 1.13 in two dimensions is summarized in Jordán and Szabadka [19].

A different set of sufficient conditions for the related concept of dimensional rigidity were described by Alfakih [2]. In [3] he showed that these conditions were equivalent to the existence of a PSD equilibrium stress matrix of maximal rank. In [3] he also showed that a generic dimensionally rigid framework (with $v \ge d+2$) must be universally rigid; this has the same effect as Lemma 1.12, and thus results in Corollary 1.13. In these papers, he also conjectured that for a generic universally rigid framework, a maximal rank PSD equilibrium stress matrix must exist.

In the related context of frameworks with pinned anchor vertices, So and Ye [30] showed the appropriate analogue of Theorem 1.11 follows from complementarity in semidefinite programming (see Sect. 5 below for more on this).

In this paper our main result is the converse to Corollary 1.13:

Theorem 1

A universally rigid framework $(p,\Gamma )$, with $p$ generic in $C^d({\mathcal V})$ and having $d+2$ or more vertices, has a PSD equilibrium stress matrix with rank $v-d-1$.

Remark 1.14

Alfakih has given an example [2, Example 3.1] showing that Theorem 1 is false if we drop the assumption that $p$ is generic. For any universally rigid framework (generic or not), it’s not hard to see that there is a non-zero PSD equilibrium stress matrix. (See [4, Theorem 5.1].) The difficulty in Theorem 1 is finding a stress matrix of high rank.

Theorems 1.11 and 1 compare nicely with the situation for global rigidity, where a framework is generically globally rigid iff it has an equilibrium stress matrix of rank $v-d-1$ (with no PSD constraint). Sufficiency was proved by Connelly [11], and necessity was proved by the authors together with Alex Healy [15].

Question 1.15

For a graph $\Gamma$ that is generic globally rigid ${\mathbb E}^d$, is there always a generic framework in $C^d({\mathcal V})$ that is universally rigid?

In this paper, we also prove more general versions of Theorem 1 in the general context of convex optimization and strict complementarity in semidefinite programming. See Theorem 2 in Sect. 4 and Theorem 3 in Sect. 5.

2 Algebraic Geometry Preliminaries

We start with some preliminaries about semi-algebraic sets from real algebraic geometry, somewhat specialized to our particular case. For a general reference, see, for instance, the book by Bochnak et al. [7].

Definition 2.1

An affine real algebraic set or variety $V$ contained in ${\mathbb R}^n$ is a subset of ${\mathbb R}^n$ that is defined by a set of algebraic equations. It is defined over ${\mathbb Q}$ if the equations can be taken to have rational coefficients. An algebraic set has a dimension $\dim (V)$, which we will define as the largest $t$ for which there is an open subset of $V$ (in the Euclidean topology) homeomorphic to ${\mathbb R}^t$.

Definition 2.2

A semi-algebraic set $S$ is a subset of ${\mathbb R}^n$ defined by algebraic equalities and inequalities; alternatively (by a non-trivial theorem), it is the image of an algebraic set (defined only by equalities) under an algebraic map. It is defined over ${\mathbb Q}$ if the equalities and inequalities have rational coefficients. Like algebraic sets, a semi-algebraic set has a well defined (maximal) dimension $t$.

We next define genericity in larger generality and give some basic properties.

Definition 2.3

A point in a (semi-)algebraic set $V$ defined over ${\mathbb Q}$ is generic if its coordinates do not satisfy any algebraic equation with coefficients in ${\mathbb Q}$ besides those that are satisfied by every point on $V$.

A point $x$ on a semi-algebraic set $S$ is locally generic if for small enough $\varepsilon$, $x$ is generic in $S \cap B_\varepsilon (x)$.

Remark 2.4

A semi-algebraic set $S$ will have no generic points if its Zariski closure over ${\mathbb Q}$ is reducible over ${\mathbb Q}$. In this case all points in each irreducible component will satisfy some specific equations not satisfied everywhere over $S$. But even in this case, almost every point in the set will be generic within its own component. Such points will still be locally generic in $S$.

We will need a few elementary lemmas on generic points in semi-algebraic sets.

Lemma 2.5

If $X$ and $Y$ are both semi-algebraic sets defined over ${\mathbb Q}$, with $X\subset Y$ and $X$ dense in $Y$ (in the Euclidean topology), then $X$ contains all of the locally generic points of $Y$.

Proof

Due to the density assumption, $Y\backslash X$ must be a semi-algebraic set defined over ${\mathbb Q}$ with dimension less than that of $Y$. The Zariski closure of a semi-algebraic set maintains its dimension, thus all points in $Y\backslash X$ must satisfy some algebraic equation that is non-zero over $Y$ and thus these points must be non-generic. To see that a point $y \in Y \setminus X$ is not locally generic either, apply this argument in an $\varepsilon$-neighborhood of $y$. (That is, apply the argument to $Y \cap B_\varepsilon (y)$ and $X \cap B_\varepsilon (y)$.)$\square$

Lemma 2.6

Let $V$ be a semi-algebraic set, $f$ be an algebraic map from $V$ to a range space $X$, and $W$ be an semi-algebraic set contained in the image of $f$, with $V$, $W$, and $f$ all defined over ${\mathbb Q}$. If $x_0\in V$ is generic and $f(x_0) \in W$, then $f(x_0)$ is generic in $W$.

Proof

Let $\phi$ be any algebraic function on $X$ with rational coefficients so that $\phi (f(x_0)) = 0$. Then $\phi \circ f$ vanishes at $x_0$, which is generic in $V$, so $\phi \circ f$ vanishes identically on $V\!$. This implies that $\phi$ vanishes on $W$. Thus any algebraic function defined over ${\mathbb Q}$ that vanishes at $f(x_0)$ must vanish on all of $W\!$. This proves that $f(x_0)$ is generic in $W\!$.$\square$

3 The Geometry of PSD Stresses

We now turn to the main construction in our proof.

3.1 The Measurement Set

Definition 3.1

The $d$-dimensional measurement set $M_d(\Gamma )$ of a graph $\Gamma$ is defined to be the image of $C^d({\mathcal V})$ under the map $\ell _\Gamma$. These are nested by $M_d(\Gamma ) \subset M_{d+1}(\Gamma )$ and eventually stabilize at $M_{v-1}(\Gamma )$, also called the absolute measurement set $M(\Gamma )$.

Since $M_d(\Gamma )$ is the image of $C^d({\mathcal V})$ under an algebraic map, by Lemma 2.6, if $p$ is generic in $C^d({\mathcal V})$ then $\ell _\Gamma (p)$ is generic in $M_d(\Gamma )$ (which must be irreducible).

Lemma 3.2

The set $M(\Gamma )$ is convex.

Proof

The squared edge lengths of a framework $p$ are computed by summing the squared edge lengths of each coordinate projection of $p$, so $M_d(\Gamma )$ is the $d$-fold Minkowski sum of $M_1(\Gamma )$ with itself. Since $M_1(\Gamma )$ is invariant under scaling by positive reals, $M_d(\Gamma )$ can also be described as an iterated chord variety, and in particular $M(\Gamma )$ is the convex hull.$\square$

A particular case of interest is $M(\Delta _v)$, the absolute measurement set of the complete graph on the vertices. It is a cone in ${\mathbb R}^{\left( {\begin{array}{c}v\\ 2\end{array}}\right) }$.

Lemma 3.3

The measurement set $M_d(\Delta _v)$ is isomorphic (as a subset of the linear space ${\mathbb R}^{\left( {\begin{array}{c}v\\ 2\end{array}}\right) }$) to the set of PSD $(v-1)\times (v-1)$ matrices of rank at most $d$.

Proof

There is a standard linear map from $M(\Delta _v)$ to the convex cone of $v-1$ by $v-1$ positive semidefinite matrices, which we recall for the reader. (See, e.g., [16, 28].) For a point $x \in M_d(\Delta _v)$, by the universal rigidity of the simplex, up to $d$-dimensional Euclidean isometry there is a unique $p\in C^d({\mathcal V})$ with $x= \ell _\Delta (p)$. If we additionally constrain the last vertex to be at the origin, then $p$ is unique up to an orthonormal transform. Think of such a constrained $p$ as a $(v-1) \times d$ matrix, denoted $\varrho$. The map sends $x$ to the matrix $\varrho \varrho ^t$, which has rank at most $d$. (The rank of $\varrho \varrho ^t$ is less than $d$ if $p$ has an affine span of dimension less than $d$.) It is easy to check that $\varrho \varrho ^t$ does not change if we change $\varrho$ by an orthonormal transform, and that in fact the entries of $\varrho \varrho ^t$ are linear combinations of the squared lengths of edges, so the map is well-defined and linear.$\square$

Definition 3.4

Let $K$ be a non-empty convex set in an affine space. The dimension of $K$ is the dimension of the smallest affine subspace containing $K$. A point $x\in K$ is in the relative interior ${{\mathrm{Int}}}(K)$ of $K$ if there is a neighborhood $U$ of $x$ in ${\mathbb E}^{e}$ so that $U\cap K\cong {\mathbb R}^{\dim K}$. (It is easy to see that the relative interior of $K$ is always non-empty.)

The face $F(x)$ of a point $x\in K$ is the (unique) largest convex set contained in $K$ so that $x \in {{\mathrm{Int}}}(F(x))$. The faces of $K$ are the sets $F(x)$ as $x$ ranges over $K$. (In Sect. 4.1 we will see more characterizations of $F(x)$.) Let $f(x)$ be the dimension of $F(x)$.

Lemma 3.5

Let $x = \ell _\Delta (p)$ with $p\in C^d({\mathcal V})$. Then $F(x) = \ell _\Delta ({{\mathrm{Aff}}}_d(p)) = \ell _\Delta ({{\mathrm{\textit{GL}}}}_d(p))$. When $p$ is proper, $f(x) = \left( {\begin{array}{c}d+1\\ 2\end{array}}\right)$.

Here ${{\mathrm{\textit{GL}}}}_d$ is the group of $d$-dimensional linear transforms, and ${{\mathrm{Aff}}}_d$ is the corresponding affine group.

Proof

By Lemma 3.3, this reduces to understanding the faces of the cone of $v-1$ by $v-1$ PSD matrices, which is well understood (see, e.g., [23, Theorem A.2]). In particular, for $\varrho$ a $(v-1)\times d$ matrix, the points in $F(\varrho \varrho ^t)$ in the semidefinite cone are those matrices of the form $\varrho L^t L \varrho ^t$ for some $d\times d$ matrix $L$. But each such $\varrho L^t L \varrho ^t$ maps under our isometry to $\ell _\Delta (\sigma )$ where $\sigma \in C^d({\mathcal V})$ is obtained from $p$ by a $d$-dimensional affine transform, with linear part described by $L$. When $p$ has an affine span of dimension $d$, $\varrho$ is of rank $d$. This implies that $F(\varrho \varrho ^t)$ has dimension $\left( {\begin{array}{c}d+1\\ 2\end{array}}\right)$, as we can see by computing the dimension of ${{\mathrm{\textit{GL}}}}_d/O_d$, the linear transforms modulo the orthonormal transforms.$\square$

3.2 Dual Vectors and PSD Stresses

Definition 3.6

Let us index each of the coordinates of ${\mathbb R}^{\left( {\begin{array}{c}v\\ 2\end{array}}\right) }$ with an integer pair $ij$ with $1 \le i<j \le v$. Given $\phi$, a functional in the dual space $\bigl ({\mathbb R}^{\left( {\begin{array}{c}v\\ 2\end{array}}\right) }\bigr )^*$, define the $v$-by-$v$ matrix $M(\phi )$ as follows: for $i \ne j$, $M(\phi )_{ij}= M(\phi )_{ji}{:=}-\phi _{ij}$ and $M(\phi )_{ii} {:=} -\sum _{j\ne i} M(\phi )_{ij}$

Lemma 3.7

Let $\phi$ be a dual vector in $\bigl ({\mathbb R}^{\left( {\begin{array}{c}v\\ 2\end{array}}\right) }\bigr )^*$ and let $\Omega {:=} M(\phi )$ be the corresponding matrix. Let $p\in C^d({\mathcal V})$. Then

$$\begin{aligned} \langle \phi , \ell _\Delta (p) \rangle = \tfrac{1}{2}\sum _{k=1}^d (p^k)^t \Omega p^k. \end{aligned}$$

(3.1)

Here we use the notation $p^k$ for vector in ${\mathbb R}^v$ describing the component of $p$ in the $k$’th coordinate direction of ${\mathbb E}^d$.

Proof

Both sides are equal to $\sum _k \sum _{i,j \mid i < j} (p^k_i-p^k_j)^2 \phi _{ij}$.$\square$

Definition 3.8

For $K\subset {\mathbb R}^n$ a convex set and $\phi$ a functional in the dual space $({\mathbb R}^n)^*$, we say that $\phi$ is tangent to $K$ at $x \in K$ if for all $y\in K$, $\langle \phi , y\rangle \ge 0$ while $\langle \phi , x\rangle =0$.

Lemma 3.9

Let $\phi$ be a dual vector in $\bigl ({\mathbb R}^{\left( {\begin{array}{c}v\\ 2\end{array}}\right) }\bigr )^*$ that is tangent to $M(\Delta _v)$ at $\ell _\Delta (p)$ for some $p\in C({\mathcal V})$. Let $\Omega {:=} M(\phi )$ be the corresponding matrix. Then $\Omega$ is a PSD equilibrium stress matrix for $(p,\Delta _v)$.

Proof

Conditions (1) and (3) in Definition 1.8 are automatic by definition of $\Omega$, and condition (2) is vacuous for the complete graph $\Delta _v$. It remains to check condition (4) and that $\Omega$ is PSD.

By Lemma 3.7, $\langle \phi , \cdot \rangle$ can be evaluated as a quadratic form using the matrix $\Omega$. Since $\langle \phi , \cdot \rangle$ is not negative anywhere on $M(\Delta _v)$, $\Omega$ must be PSD. Because $\Omega$ is positive semidefinite and $\sum _{k=1} (p^k)^t \Omega p^k=0$, it must also be true that for each $k$, $(p^k)^t \Omega p^k = 0$ and so $\Omega p^k =0$, which is the last necessary condition to show $\Omega$ is an equilibrium stress matrix.$\square$

Lemma 3.10

In the setting of Lemma 3.9, suppose furthermore that $\phi$ is only tangent to points in $F(\ell _\Delta (p))$, and suppose the affine span of $p$ has dimension $d$.

Then $\Omega$ is a PSD equilibrium stress matrix for $(p,\Delta _v)$ with rank $v-d-1$.

Proof

From Lemma 3.9, $\Omega$ is a PSD equilibrium stress matrix for $(p,\Delta _v)$. By assumption, its kernel is spanned by the coordinates of frameworks that map under $\ell _\Delta$ to $F(\ell _\Delta (p))$. From Lemma 3.5, such frameworks are $d$-dimensional affine transforms of $p$. Thus the kernel is spanned by the $d$ coordinates of $p$ and the all-ones vector. Since the kernel has dimension $d+1$, $\Omega$ has rank $v-d-1$.$\square$

Lemma 3.11

In the setting of Lemma 3.10, suppose furthermore that $\phi _{ij}=0$ for $\{i,j\} \not \in {\mathcal E}(\Gamma )$ for a graph $\Gamma$.

Then $\Omega$ is a positive semidefinite equilibrium stress matrix for $(p,\Gamma )$ with rank $v-d-1$.

Proof

$\Omega$ must have zeros in all coordinates corresponding to non-edges in $\Gamma$, thus it will be an equilibrium stress matrix for $\Gamma$ as well as for $\Delta _v$. The rest follows from Lemma 3.10.$\square$

To be able to use Lemma 3.11, we want to find a dual vector $\phi$ that is only tangent to points in $F(\ell _\Delta (p))\subset M(\Delta _v)$. Additionally we need that $\phi _{ij}=0$ for $\{i,j\} \not \in {\mathcal E}$. As we will see, this will correspond to finding a dual vector in $({\mathbb R}^e)^*$ that is only tangent to points in $F(\ell _\Gamma (p)) \subset M(\Gamma )$. The proper language for this kind of condition is the notion of convex extreme and exposed points, which we turn to next.

4 Convex Sets and Projection

We will prove our main theorems in the more general setting of closed convex cones. Our goal is the following general theorem about projections of convex sets, which will quickly imply Theorem 1. (See Definitions 4.1, 4.6, and 4.11 for the terms used.)

Theorem 2

Let $K$ be a closed line-free convex semi-algebraic set in ${\mathbb R}^m$, and $\pi : {\mathbb R}^m \rightarrow {\mathbb R}^n$ a projection, both defined over ${\mathbb Q}$. Suppose $x$ is locally generic in ${{\mathrm{ext}}}_k(K)$ and universally rigid under $\pi$. Then $\pi (x)$ is $k$-exposed.

4.1 Extreme Points

Definition 4.1

Let $K$ be a non-empty, convex set. A point $x\in K$ is $k$ -extreme if $f(x) \le k$. (Recall from Definition 3.4 that $f(x)$ is the dimension of the face of $K$ containing $x$.) Let ${{\mathrm{ext}}}_k(K)$ be the set of $k$-extreme points in $K$.

We will also use the following elementary propositions (see for example the exercises in chapter 2.4 of [17].)

Proposition 4.2

For $K$ a convex set and $x \in K$, the following statements are equivalent:

• $f(x) \le k$, and

• $x$ is not in the relative interior of any non-degenerate $(k+1)$-simplex contained in $K$.

Proposition 4.3

For $K$ a convex set and $x\in K$, the face $F(x)$ is the set of points $z \in K$ so that there is an $z' \in K$ with $x$ in the relative interior of the segment $[z', z]$.

Remark 4.4

One special case of Proposition 4.3 is when $z=x$, in which case we also take $z'=x$ and the segment consists of a single point.

Corollary 4.5

For $K$ a convex set, the faces of $K$ are the convex subsets $F$ of $K$ such that every line segment in $K$ with a relative interior point in $F$ has both endpoints in $F$.

4.2 Exposed Points

Definition 4.6

A point $x\in K$ is $k$ -exposed if there is a closed half-space $H$ containing $x$ so that $\dim H \cap K \le k$. Let $\exp _k(K)$ be the set of $k$-exposed points in $K$.

See Fig. 2 for some examples of $k$-extreme and $k$-exposed points, including a case where they differ. If $x$ is $k$-exposed, it is also $k$-extreme, as any simplex containing $x$ in its relative interior is contained in any supporting hyperplane.

Fig. 2

Examples of extreme and exposed points. For the racetrack shape illustrated (bounded by semi-circles and line segments), $a$ is $0$-extreme and $0$-exposed, $b$ is $1$-extreme and $1$-exposed, $c$ is $2$-extreme and $2$-exposed, and $d$ is $0$-extreme and $1$-exposed

The following theorem is a crucial tool in our proof.

Theorem 4.7

(Asplund [5]) For $K$ a closed convex set, the $k$-exposed points are dense in the $k$-extreme points.

Remark 4.8

Asplund only states and proves Theorem 4.7 for compact convex sets. The result follows for any closed convex set $K$ as follows. For $x\in {{\mathrm{ext}}}_k(K)$, fix $R > 0$ and consider the compact convex set $K' {:=} K \cap \overline{B}_R(x)$. Then Asplund’s theorem says we can find $k$-exposed points $z$ in $K'$ that are arbitrarily close to $x$. If $z$ is sufficiently close to $x$ (say, within $R/2$ of $x$), it will also be $k$-exposed in $K$, as desired.

Theorem 4.7 is an extension of a theorem of Straszewicz [29], who proved it in the case $k=0$. There are several improvements of Theorem 4.7, replacing “dense” with various stronger assertions. In our applications we will consider semi-algebraic sets $K$ defined over ${\mathbb Q}$. Note that for any such set $K$, ${{\mathrm{ext}}}_k(K)$ and $\exp _k(K)$ are also semi-algebraic over ${\mathbb Q}$, as the $k$-extreme and $k$-exposed conditions can be phrased algebraically.

Corollary 4.9

Let $K$ be a closed, convex, semi-algebraic set. If $x$ is locally generic in ${{\mathrm{ext}}}_k(K)$, then $x$ is $k$-exposed.

Proof

This follows from an application of Lemma 2.5 to the inclusion $\exp _k(K) \subset {{\mathrm{ext}}}_k(K)$ in a small neighborhood around $x$.$\square$

4.3 Projection

The two convex sets $M(\Delta _v)$ and $M(\Gamma )$ are related by a projection from ${\mathbb R}^{\left( {\begin{array}{c}n\\ 2\end{array}}\right) }$ to ${\mathbb R}^e$. We will consider this situation more generally.

Throughout this section, fix two Euclidean spaces, ${\mathbb E}^m$ and ${\mathbb E}^n$, with a surjective projection map $\pi : {\mathbb E}^m \rightarrow {\mathbb E}^n$ and a closed convex set $K \subset {\mathbb E}^m$. We will work with the image $\pi (K) \subset {\mathbb E}^n$. Let $\pi _K$ be the restriction of $\pi$ to $K$.

Remark 4.10

In general, $\pi (K)$ need not be closed, even if $K$ is. We continue to work with $\pi (K)$ and its “faces” as defined in Definition 3.4, even if it is not closed.

Definition 4.11

We say that $x\in K$ is universally rigid (UR) under $\pi$ if $\pi _K^{-1}(\pi (x))$ is the single point $x$.

Note that for $y \in \pi (K)$, $\pi _K^{-1}(y)$ is always a convex set in its own right.

Lemma 4.12

Let $K$ be a convex set and $\pi$ a projection. For any $x\in K$, $\pi (F(x)) \subset F(\pi (x))$.

Proof

The set $\pi (F(x))$ is a convex set containing $\pi (x)$ in its relative interior, so by definition is contained in $F(\pi (x))$.$\square$

A point that is $0$-extreme in a convex set is called a vertex of the set. A convex set is line free if it contains no complete affine line. Recall that a non-empty, closed, line-free convex set has a vertex (see e.g., [17, 2.4.6]). Our convex sets of interest, $M(K_\Delta )$ and $M(\Gamma )$, are closed and also automatically line free, as the length-squared takes only positive values and any line contains both positive and negative values in at least one coordinate.

Proposition 4.13

Let $K$ be a convex set and $\pi$ a projection. For any $y \in \pi (K)$ and $x$ a vertex of $\pi _K^{-1}(y)$, $F(x)$ maps injectively under $\pi _K$ into $F(y)$. In particular, $f(x) \le f(y)$. If $K$ is closed and line free, then for every $y \in \pi (K)$ there is a $x \in \pi ^{-1}(y)$ so that $f(x) \le f(y)$.

Proof

Let $A(x)$ be the smallest affine subspace containing $F(x)$. Suppose $A(x)$ contained a direction vector $v$ in the kernel of $\pi$. Then, since $x$ is in the relative interior of $F(x)$ for small enough $\varepsilon$, we would have the segment $[x+\varepsilon v,x-\varepsilon v]$ contained in $F(x)$ and also in $\pi _K^{-1}(y)$. This would contradict the assumption that $x$ is a vertex of $\pi _K^{-1}(y)$. Thus $F(x)$ maps injectively under $\pi _K$.

From Lemma 4.12 we see that $f(x) \le f(y)$. For the last part of the lemma, observe that if $K$ is closed and line free, so is $\pi _K^{-1}(y)$, and so $\pi _K^{-1}(y)$ has a vertex, which is the desired point $x$ by the first part.$\square$

Proposition 4.14

Let $K$ be a convex set and $\pi$ a projection. For any $y \in \pi (K)$ and $x$ in the relative interior of $\pi _K^{-1}(y)$, $F(x) = \pi _K^{-1}(F(y))$. In particular, $f(x) \ge f(y)$.

Proof

By Lemma 4.12, we already know that $F(x) \subset \pi _K^{-1}(F(y))$, so we just need to show the other inclusion. Pick any $y_1 \in F(y)$ and $x_1 \in \pi _K^{-1}(y_1)$. We must show that $x_1 \in F(x)$. Since $y_1 \in F(y)$, by Proposition 4.3 there is an $y_2 \in \pi (K)$ so that $y \in {{\mathrm{Int}}}([ y_1,y_2])$. Let $x_2 \in \pi _K^{-1}(y_2)$. Let $x' \in K$ be the (unique) point of intersection of $[x_1, x_2]$ with $\pi _K^{-1}(y)$. Since $x \in {{\mathrm{Int}}}(\pi _K^{-1}(y))$, there is a point $x''\in \pi _K^{-1}(y)$ with $x \in {{\mathrm{Int}}}([x', x''])$. But then $x$ is in the interior of the simplex $[x_1, x_2, x'']$, which implies that $x_1\in F(x)$.$\square$

In order to be able to apply Asplund’s theorem at $\pi (x)$ we need $\pi (x)$ to be locally generic in ${{\mathrm{ext}}}_k(\pi (K))$. The following lemma will assist us.

Lemma 4.15

Let $K$ be a closed, convex set in ${\mathbb R}^m$ and let $\pi _K: K \rightarrow {\mathbb R}^n$ be a projection. Let $x\in K$ be universally rigid under $\pi$. Then for any $\varepsilon$ there is a $\delta > 0$ so that $\pi _K^{-1}(B_\delta (\pi (x))) \subset B_\varepsilon (x) \cap K$.

Intuitively, the only points in $K$ that map close to $\pi (x)$ are close to $x$.

Proof

Suppose not. Then there is an $\varepsilon$ and a sequence of points $x_i$ with the following property: $\pi (x_i)$ approach $\pi (x)$, while $d(x,x_i) > \varepsilon$. Let $x_i'$ be the point on the interval $[x,x_i]$ that is a distance exactly $\varepsilon$ from $x$. By convexity $x_i' \in K$. Then the $x_i'$ are in a bounded and closed set and therefore have an accumulation point $x'\in K$, which will also have distance $\varepsilon$ from $x$. By the linearity of $\pi$ the $\pi (x'_i)$ also approach $\pi (x)$. So by continuity $\pi (x')=\pi (x)$. This contradicts the universal rigidity of $x$.$\square$

And now we can prove the following.

Lemma 4.16

Let $K$ be a closed line-free convex semi-algebraic set in ${\mathbb R}^m$ and $\pi : {\mathbb R}^m \rightarrow {\mathbb R}^n$ a projection, both defined over ${\mathbb Q}$. Suppose $x$ is locally generic in ${{\mathrm{ext}}}_k(K)$ and universally rigid under $\pi$. Then $\pi (x)$ is locally generic in ${{\mathrm{ext}}}_k(\pi (K))$.

Proof

By Proposition 4.13, ${{\mathrm{ext}}}_k(\pi (K)) \subset \pi ({{\mathrm{ext}}}_k(K))$. By Proposition 4.14 and the universal rigidity of $x$, we have that $\pi (x)$ is in ${{\mathrm{ext}}}_k(\pi (K))$.

Let $V {:=} {{\mathrm{ext}}}_k(K) \cap B_\varepsilon (x)$ and $W{:=} {{\mathrm{ext}}}_k(\pi (K)) \cap B_\delta (\pi (x))$. For sufficiently small $\varepsilon$, by local genericity, $x$ is generic in $V$. Meanwhile, $W \subset \pi ({{\mathrm{ext}}}_k(K))$, and, from Lemma 4.15, for small enough $\delta$, we have $\pi _K^{-1}(W) \subset B_\varepsilon (x)$ and thus $W \subset \pi (V)$.

Thus from Lemma 2.6, we have $\pi (x)$ generic in $W$. Thus $\pi (x)$ is locally generic in ${{\mathrm{ext}}}_k(\pi (K))$.$\square$

Remark 4.17

In our special case where $K$ is the cone of positive semidefinite matrices, $x$ is in fact generic in ${{\mathrm{ext}}}_k(K)$ (which is irreducible), and thus the second paragraph in the above proof (and in turn Lemma 4.15) are not needed.

Finally, in order to be able to apply Asplund’s theorem to $\pi (K)$ we need $\pi (K)$ to be a closed set. In the graph embedding case, we can use the fact that $\pi$ is a proper map whenever $\Gamma$ is connected, and thus $\pi (K)$ must be closed. In the setting of a general $K$ and $\pi$ we can argue closedness using standard techniques.

Definition 4.18

A direction of recession $v$ for a convex set $K$ is a vector such that for every (equivalently, any) $x \in K$ and every $\lambda \ge 0$ we have $x + \lambda v \in K$ (see e.g. [26, Chapter 8]).

A sufficient condition for closedness is given by the following theorem [26, Theorem 9.1].

Theorem 4.19

Let $K$ be a line free closed convex set and $\pi$ a projection. If $K$ does not have a direction of recession $v$ with $\pi (v)=0$, then then $\pi (K)$ is closed.

Corollary 4.20

Let $K$ be a line free closed convex set and $\pi$ a projection. If there is a point $x\in K$ that is universally rigid under $\pi$, then $\pi (K)$ is closed.

Proof

Suppose there was a direction of recession $v$ for $K$ with $\pi (v)=0$. Then $\pi (x + v) = \pi (v)$ with $x+v$ in $K$. This would contradict the universal rigidity of $x$. $\square$

Putting this all together, we can deduce Theorem 2.

Proof

(Proof of Theorem 2) From Corollary 4.20, $\pi (K)$ is closed. From Lemma 4.16, $\pi (x)$ is locally generic in ${{\mathrm{ext}}}_k(\pi (K))$. Thus by Corollary 4.9, $\pi (x)$ is $k$-exposed.$\square$

4.4 Proof of Main Theorem

We are now in position to complete the proof of Theorem 1. Recall that we have a universally rigid framework $(p,\Gamma )$ with $p$ generic in $C^d({\mathcal V})$. Let $K$ be $M(\Delta _v)$, and $\pi$ be its projection to $M(\Gamma )$, $k$ be $\left( {\begin{array}{c}d+1\\ 2\end{array}}\right)$. and $x \in M_d(\Delta _v) \subset K$ be $\ell _\Delta (p)$. The assumption that $p$ is generic in $C^d({\mathcal V})$ implies that $x$ is generic in $M_d(\Delta _v) = {{\mathrm{ext}}}_k(K)$.

From Theorem 2, $\pi (x)$ is $k$-exposed. So there must be a closed halfspace $H$ in ${\mathbb R}^e$ whose intersection with $\pi (K)$ is exactly $F(\pi (x))$.

The preimage $\pi ^{-1}(H)$ is a closed halfspace in ${\mathbb R}^{\left( {\begin{array}{c}v\\ 2\end{array}}\right) }$ whose intersection with $K$ is exactly $\pi _K^{-1}(F(\pi (x)))$, which by Proposition 4.14 is $F(x)$. Since $K$ is a cone, $\pi ^{-1}(H)$ must also include the origin. When $v>d+1$, then $F(x)$ is not the entire measurement cone $M(\Delta _v)$, and the halfspace $\pi ^{-1}(H)$ must not include any interior points of $M(\Delta _v)$.

Thus $\pi ^{-1}(H)$ is represented by a dual vector $\phi \in \bigl ({\mathbb R}^{\left( {\begin{array}{c}v\\ 2\end{array}}\right) }\bigr )^*$, in the sense that $\pi ^{-1}(H) \!=\! \bigl \{\,x \in {\mathbb R}^{\left( {\begin{array}{c}v\\ 2\end{array}}\right) } \mathbin {\big \vert } \phi (x) \!\le \! 0\,\bigr \}$. Moreover, this $\phi$ is tangent to $M(\Delta _v)$ exactly at $F(x)$.

Since we started with a halfspace in ${\mathbb R}^e$, $\phi _{ij} =0$ for $\{i,j\} \not \in {\mathcal E}$. From Lemma  3.11, then, $\Omega {:=} M(\phi )$ must be a positive semi-definite equilibrium stress matrix of $(p,\Gamma )$ with rank $v-d-1$.

5 Relation to Semidefinite Programming

Theorem 1 can be interpreted as a strict complementarity statement about a particular semidefinite program (SDP) and its associated dual program, as we will now explain. For a general survey on semidefinite programming see Vandenberghe and Boyd [31]. Our notation is similar to that of Pataki and Tunçel [24]. For a related discussion on universal rigidity, semidefinite programming and complementarity, see, for instance, the paper by So and Ye [30].

5.1 Semidefinite Programming

We first recall the basic definitions of semidefinite programming. Let $S^n$ be the linear space of all symmetric $n$-by-$n$ matrices and $S^n_+ \subset S^n$ be the cone of positive semidefinite matrices. A semidefinite program is given by a triple $(L,b,\beta )$ where $L \subset S^n$ is a linear subspace, $b \in S^n$ is a matrix, and $\beta \in (S^n)^*$ is a dual to a matrix (which we can also view as a matrix, using the natural inner product $\langle A, B \rangle = {{\mathrm{tr}}}(A^t B) = \sum _{i,j} A_{ij} B_{ij}$). This describes a primal constrained optimization problem:

$$\begin{aligned} \inf _x \big \{\langle \beta ,x\rangle \mid x \in (L+b) \cap S^n_+ \big \}. \end{aligned}$$

That is, we optimize a linear functional over all symmetric positive semidefinite matrices $x$, subject to the constraint that $x$ lies in a chosen affine space.

Associated with every primal SDP is the (Lagrangian) dual program

$$\begin{aligned} \inf _\Omega \big \{\langle \Omega ,b\rangle \mid \Omega \in (L^{\perp }+\beta ) \cap (S^n_+)^*\big \}. \end{aligned}$$

Since the cone of PSD matrices is self-dual, elements of $(S^n_+)^*$ also correspond to PSD matrices, so this dual program can be thought of as a semidefinite program itself.

Definition 5.1

We say a pair of primal/dual points $(x,\Omega )$ with $x \in S^n_+$ and $\Omega \in (S^n_+)^*$ are a complementary pair for the program $(L,b,\beta )$ if both are feasible points for the respective programs and $\langle \Omega ,x\rangle =0$.

A calculation shows that for any feasible primal/dual pair of points $(x,\Omega )$, we have $\langle \beta ,b\rangle -\langle \Omega ,b\rangle \le \langle \beta ,x\rangle$ and that complementarity implies $\langle \beta ,b\rangle -\langle \Omega ,b\rangle = \langle \beta ,x\rangle$.

Thus, writing the dual problem in the alternative form

$$\begin{aligned} \sup _\Omega \big \{ \langle \beta ,b\rangle -\langle \Omega ,b\rangle \mid \Omega \in (L^{\perp }+\beta ) \cap (S^n_+)^*\big \} \end{aligned}$$

we see that a complementary pair must represent optimal solutions to the primal and dual SDPs respectively.

Definition 5.2

We say that an SDP problem $(L,b,\beta )$ is gap free if it has complementary pairs of solutions.

Gap freedom is typically seen as a fairly mild constraint on an SDP problem.

For every complementary pair $(x,\Omega )$ we have [1]

$$\begin{aligned} {{\mathrm{rank}}}(x) + {{\mathrm{rank}}}(\Omega ) \le n. \end{aligned}$$

(5.1)

Definition 5.3

A complementary pair $(x,\Omega )$ is said to be strictly complementary if we have ${{\mathrm{rank}}}(x) + {{\mathrm{rank}}}(\Omega )= n$.

There is a rich theory on when SDPs have strictly complementary solution pairs. (See [1, 22, 24]; see also Sect. 5.8.) In particular, certain SDP algorithms converge more quickly on problems that satisfy strict complementarity [21]. The linear programming counterpart of strict complementarity is strict complementary slackness [13]. In the linear case, strict complementarity is always achieved. By contrast, for SDP problems it depends on the particular problem.

5.2 Graph Embedding as an SDP

In the context of graph embedding, suppose we are looking for a configuration of unconstrained dimension, $p\in C^{v}({\mathcal V})/{{\mathrm{Eucl}}}(v)$, such that the framework of $\Gamma$ is constrained to have a set of squared edge lengths $d^2_{ij}$ for $ij\in {\mathcal E}(\Gamma )$. It is well known that we can set up this graph embedding problem as a semidefinite program [20], as we will now review.

To a configuration $p$ we can associate a $v \times v$ Gram matrix $x$, with $x_{ij} = p(i) \cdot p(j)$. The Gram matrix of $p$ is unchanged by elements of $O(v)$ (although it does change when $p$ is translated). The matrix rank, $r$, of such an $x$ is the dimension of the linear span of the associated configuration $p$. This will be typically be $d+1$; one greater than the affine span, $d$, of the framework.

In the graph embedding SDP, we set $n{:=} v$ and take the Gram matrix $x$ as our unknown. The distance constraint at an edge $ij$ can be expressed as the linear constraint $x_{ii}+x_{jj}-2x_{ij}=(d_{ij})^2$. The collection of matrices satisfying these constraints for all edges forms an affine space; we choose $L$ and $b$ such that $L+b$ is this affine space. In our context, we are only interested in feasibility, and thus have no objective function, so we set $\beta {:=} 0$. Note that semidefinite programs do not allow us to explicitly constrain the rank of the solution (which is related to the dimension of the configuration).

Let us now look at the dual program to our graph embedding SDP problem. In the primal problem, the linear space $L$ corresponds to symmetric matrices $x$ with $x_{ii}+x_{jj}-2x_{ij}=0$ for all $\{i,j\} \in {\mathcal E}(\Gamma )$. Thus the space $L^\perp$, when represented as matrices, is spanned by a basis elements $B_{ij} = -e_{ii}+e_{ij}+e_{ji}-e_{jj}$ for $\{i,j\}\in {\mathcal E}(\Gamma )$, where $e_{ij}$ is the elementary matrix with a $1$ in the $ij$ entry and $0$ elsewhere. The space $L^\perp$ is therefore those matrices $\Omega$ with row-sums of zero and with $\Omega _{ij} = 0$ for all $i \ne j$, $\{i,j\} \notin {\mathcal E}(\Gamma )$. That is, $L^\perp$ is the space of all (not necessarily equilibrium) stress matrices. We also have $\beta =0$, so we optimize over these matrices.

Minimizing $\langle \Omega , b\rangle$ imposes the further constraint that the solution be an equilibrium stress matrix. This can be seen as follows. Since $\beta =0$, the all-zeros matrix is dual feasible. Whenever there is some primal feasible $x$ corresponding to a configuration $p$, the SDP must be gap free as $\langle 0, x\rangle =0$, and the optimal $\Omega$ are the feasible $\Omega$ with $\langle \Omega , x\rangle =0$. For any $\Psi \in (S^n_+)^*$ we have $\langle \Psi , x\rangle = \tfrac{1}{2}\sum _{k=1}^r (p^k)^t \Psi p^k$. (Here we use the notation $p^k$ for vector in ${\mathbb R}^n$ describing the component of $p$ in the $k$’th coordinate direction of ${\mathbb R}^r$.) And thus, as in Lemma 3.9, the feasible $\Omega$ with $\langle \Omega , x\rangle =0$ are the PSD equilibrium stress matrices for $(p,\Gamma )$.

In this language we can restate Theorem 1 as follows.

Proposition 5.4

Let $p$ be generic in $C^d({\mathcal V})$, let $(p,\Gamma )$ be universally rigid in $E^d$, and let $(L,b,0)$ be the associated SDP using the graph $\Gamma$ and the distances of the edges in $(p,\Gamma )$. Then $(L,b,0)$ has a strictly complementary solution pair $(x,\Omega )$.

Proof

Simply let $x$ be the Gram matrix corresponding to a translation of $p$ such that its affine span does not include the origin. Thus $x$ will have rank $d+1$. Let $\Omega$ be a PSD equilibrium stress matrix of rank $v-d-1$, which exists by Theorem 1. Then ${{\mathrm{rank}}}x + {{\mathrm{rank}}}\Omega = v$.$\square$

5.3 SDP Feasibility

Our discussion of universal rigidity and equilibrium stress matrices carries over directly to any SDP feasibility problem $(L,b,0)$ (i.e., where $\beta =0$). To see this we first set up some notation. Pick an integer $r > 0$ and let $k{:=} \left( {\begin{array}{c}r+1\\ 2\end{array}}\right)$. Then, as in Lemma 3.5, ${{\mathrm{ext}}}_k(S^n_+)$ is the set of the PSD matrices of rank less than or equal to $r$, which we will denote $S^n_{+r}$. Let $\pi$ be projection from $S^n$ to $S^n/L$, and $\pi _+$ its restriction to $S^n_+$. A point $x \in S^n_+$ is a solution to the feasibility problem iff $\pi (x) = \pi (b)$, or $x \in \pi _+^{-1}(\pi (b))$.

We say that a point $x \in S^n_+$ is universally rigid under $\pi$ iff $\pi _+^{-1}(\pi (x))$ is a single point: A universally rigid feasible point is the unique feasible solution to $(L,b,0)$. As we vary $b$ with fixed $L$, we will see as solutions all points in $S^n_+$; it may happen that for some $b$ there is a unique, generic feasible solution.

Proposition 5.5

Let $(L,b,0)$ be an SDP feasibility problem, where $L$ has rational coefficients. Suppose there is a unique feasible solution $x$ which is generic in $S^n_{+r}$. Then there exists an optimal dual solution $\Omega$ such that $(x,\Omega )$ is a strictly complementary pair.

Proof

Since $x$ is generic in $S^n_{+r} = {{\mathrm{ext}}}_k(S^n_+)$, by Theorem 2 $\pi (x)$ is $k$-exposed. Thus there is a PSD matrix $\Omega$ in $(S^n/L)^*=L^\perp$ that is tangent to $\pi (S^n_+)$ at $\pi (x)$, with contact $F(\pi (x))$. Since $\Omega \in L^\perp$, it is a feasible point of the dual SDP. Since $\Omega$ is tangent to $\pi (S^n_+)$ at $\pi (x)$, it is also tangent to $S^n_+$ at $x$; thus $\langle \Omega , x\rangle =0$ and $\Omega$ is a complementary and therefore optimal dual solution.

The tangency of $\Omega$ to $S^n_+$ at $x$ has contact $\pi ^{-1}_+(F(\pi (x))$ which, by Proposition 4.14, is $F(x)$. Let $p$ be an $r$-dimensional configuration of $n$ points with Gram matrix $x$. From the facial stucture of the PSD cone we see that $F(x)$ consists only of Gram matrices of $r$-dimensional linear transforms of $p$. We also have the relation $\langle \Omega , x\rangle = \tfrac{1}{2}\sum _{k=1}^r (p^k)^t \Omega p^k = 0$. Thus we see that $\Omega$ must have a kernel of dimension $r$ and have rank $n-r$.$\square$

5.4 SDP Optimization

We can apply the approach above to a more general SDP problem $(L,b,\beta )$, where $\beta \ne 0$. Specifically, we prove the following.

Theorem 3

Let $(L,b,\beta )$ be a gap-free SDP problem, with $L$ and $\beta$ rational. Suppose there is a unique optimal solution $x$ which is generic in $S^n_{+r}$. Then there exists a strictly complementary pair $(x, \Omega )$.

We will prove the theorem by reducing to the $\beta =0$ case. For any SDP optimization problem $(L,b,\beta )$ with an optimal solution $x$, there is an associated SDP feasibility problem $(L', b', 0)$, where $L' + b'$ is $\{ y \in L + b \mid \langle \beta , y\rangle = \langle \beta , x\rangle \}$. In particular, $L'$ is $L \cap \ker \beta$ (which is still rational) and the dual space $L'^\perp$ is $L^\perp + \langle \beta \rangle$. Then feasible solutions to $(L', b', 0)$ correspond to optimal solutions to $(L, b, \beta )$.

Lemma 5.6

Let $(L,b,\beta )$ be an SDP problem, with $L$ and $\beta$ rational. Suppose there is a unique optimal solution $x$ which is generic in $S^n_{+r}$. Then there exists a PSD $\Omega$ such that ${{\mathrm{rank}}}\Omega = n-r$, with $\Omega \in L^\perp + \langle \beta \rangle$ and $\langle \Omega ,x\rangle =0$.

Proof

Apply Proposition 5.5 to the feasibility problem $(L', b', 0)$ constructed above. This gives a $\Omega \in L'^\perp = L^\perp + \langle \beta \rangle$ that is strictly complementary to $x$.$\square$

Note that we have not yet proved Theorem 3, as Lemma 5.6 gives $\Omega$ in the linear space $L^\perp + \langle \beta \rangle$ rather than the desired affine space $L^\perp + \beta$.

Proof

(Proof of Theorem 3) Let $\Omega _1$ be the PSD matrix given by Lemma 5.6. From the assumption of gap freedom there exists a PSD $\Omega _2$ with $\Omega _2 \in L^\perp + \beta$ and $\langle \Omega _2,x\rangle =0$. Thus for any positive scalars $\lambda _1$ and $\lambda _2$, the matrix $\Omega {:=} \lambda _1 \Omega _1 + \lambda _2 \Omega _2$ is PSD, has ${{\mathrm{rank}}}$ no less than $n-r$, and has $\langle \Omega ,x\rangle =0$. By adjusting $\lambda _1$ and $\lambda _2$ we can achieve $\Omega \in L^\perp + \beta$. By Equation (5.1), we in fact have ${{\mathrm{rank}}}\Omega = n-r$.$\square$

We note though that for a given $(L,\beta )$ and rank $r$, as we vary $b$, there may be no unique solutions with rank $r$. Even if there are such $x$, they may all be non-generic. In such cases, Theorem 3 is vacuous, as there are no choices of $(L, b, \beta )$ satisfying the hypotheses.

5.5 Genericity

In the context of SDP optimization, the hypothesis in Theorem 3 that $L$ and $\beta$ be rational may seem a little unnatural. This hypothesis can be relaxed if we work with points that are generic over a field that is larger than ${\mathbb Q}$.

Definition 5.7

Let ${\mathbf {k}}$ be a field containing ${\mathbb Q}$ and contained in ${\mathbb R}$. A semi-algebraic set $S \subset {\mathbb R}^n$ is defined over ${\mathbf {k}}$ if there is a set of equalities and inequalities defining $S$ with coefficients in ${\mathbf {k}}$. If $S$ is defined over ${\mathbf {k}}$, a point $x \in S$ is generic over ${\mathbf {k}}$ if the coordinates of $x$ do not satisfy any algebraic equation with coefficients in ${\mathbf {k}}$ beyond those that are satisfied by every point in $S$. Similarly, $x$ is locally generic over ${\mathbf {k}}$ if for small enough $\varepsilon$, $x$ is generic in $S \cap B_\varepsilon (x)$.

A defining field of a semi-algebraic set $S$, written ${\mathbb Q}[S]$, is any field over which it is defined. (There is a unique smallest field for algebraic sets by a result of Weil [32, Corollary IV.3]. For our purposes, we can use any field over which $S$ is defined.) Similarly, if $f : X \rightarrow Y$ is a map between semi-algebraic sets, then ${\mathbb Q}[f]$ is a field over which it is defined (or, equivalently, a field over which the graph of $f$ is defined).

For instance, if $S$ is a single point $x$, we can take ${\mathbb Q}[S]$ to be the same as ${\mathbb Q}[x]$, the smallest field containing all the coordinates of $x$. Also, if $x$ is generic over ${\mathbb Q}$, then $y$ is generic over ${\mathbb Q}[x]$ iff the pair $(x,y)$ is generic over ${\mathbb Q}$.

With this definition, Theorems 2 and 3 can be improved to allow non-rational sets and projections.

Theorem 2

Let $K$ be a closed line-free convex semi-algebraic set in ${\mathbb R}^m$, and $\pi : {\mathbb R}^m \rightarrow {\mathbb R}^n$ a projection. Suppose $x$ is locally generic over ${\mathbb Q}[K,\pi ]$ in ${{\mathrm{ext}}}_k(K)$ and universally rigid under $\pi$. Then $\pi (x)$ is $k$-exposed.

Theorem 3

Let $(L,b,\beta )$ be a gap-free SDP problem. Suppose there is a unique optimal solution $x$ which is generic over ${\mathbb Q}[L,\beta ]$ in $S^n_{+r}$. Then there exists a strictly complementary pair $(x, \Omega )$.

The proofs follow exactly the proofs of the versions given earlier. For instance, in Theorem $3'$, we apply Theorem $2'$ to the cone $S^n_+$ (which is defined over ${\mathbb Q}$) and the projection onto $S^n/(L + \langle \beta \rangle )$, which is defined over whatever field is needed to define $L$ and $\beta$.

5.6 Relation to Previous Results

A fundamental result of [1, 24] on strict complementarity can be summarized as follows.

Theorem 5.8

Suppose $(L,b,\beta )$ is a generic SDP program that is gap free. Then $(L,b,\beta )$ admits a strictly complementary pair of solutions.

This result is neither stronger nor weaker than our Theorem 3. In particular Theorem 5.8 requires that all parameters be generic. In contrast, Theorem 3 does not assume genericity of any of the parameters but rather assumes genericity of the solution within its rank. Indeed, in our application to rigidity of graphs, $\beta =0$, which is obviously not generic. (The parameter $b$ is also not usually generic.) In fact, there are very few situations where both theorems can apply, as the following proposition shows.

Proposition 5.9

In an SDP problem $(L,b,\beta )$ with $\dim L = D$ and primal solution $x$ of rank $r$, if Theorem 5.8 applies, then

$$\begin{aligned} \left( {\begin{array}{c}n-r+1\\ 2\end{array}}\right) \le D. \end{aligned}$$

On the other hand, if Theorem 3 applies, then

$$\begin{aligned} \left( {\begin{array}{c}n-r+1\\ 2\end{array}}\right) \ge D. \end{aligned}$$

Proof

For a given $(L,b,\beta )$, if $b$ is generic over ${\mathbb Q}[L]$, then $r$ satisfies the first inequality, as described in [1, Theorem 12] and [22, Proposition 5]. In particular, for generic $b$, the intersection of $L+b$ with $S^n_{+r}$ must be transversal, which from a dimension count gives the first inequality. This takes care of the first part of the proposition. (If $\beta$ is generic over ${\mathbb Q}[L]$, as in Theorem 5.8, there is also an upper bound on $r$: $\left( {\begin{array}{c}r+1\\ 2\end{array}}\right) \le \left( {\begin{array}{c}n+1\\ 2\end{array}}\right) -D$. But we do not need this.)

For the second part, recall that if Theorem 3 applies, there is a point $x$, generic over ${\mathbb Q}[L,\beta ]$ in $S^n_{+r}$ which is the unique solution to the SDP problem $(L, b, \beta )$. Recall that there is an associated feasibility problem $(L', b', 0)$. Let $\pi : S^n \rightarrow S^n/L'$ be the associated projection and $\pi _+$ its restriction to $S^n_+$. Since $x$ is unique (in both $(L,b,\beta )$ and $(L',b',0)$), $x$ is the only point in $S^n_+$ mapping to $\pi (x)$, and $\pi (x) \in {\partial }\pi (S^n_+)$. Moreover, since $x$ is generic in $S^n_{+r}$, there is an open neighborhood $U$ of $x$ in $S^n_{+r}$ with these properties. In particular, $U$ maps injectively by $\pi$ to ${\partial }\pi (S^n_+) \subset S^n/L'$.

$S^n_{+r}$ has dimension $\left( {\begin{array}{c}n+1\\ 2\end{array}}\right) -\left( {\begin{array}{c}n-r+1\\ 2\end{array}}\right)$. On the other hand, $\dim (S^n/L') \le \left( {\begin{array}{c}n+1\\ 2\end{array}}\right) -D+1$ (with equality iff $\beta \not \in L^\perp$ or equivalently $L' \ne L$), so $\dim (\partial \pi (S^n_+))\le \left( {\begin{array}{c}n+1\\ 2\end{array}}\right) -D$. If there is a smooth injection from $S^n_{+r}$ to $\partial \pi (S^n_+)$, we must have $\left( {\begin{array}{c}n-r+1\\ 2\end{array}}\right) \ge D$, as desired.$\square$

5.7 Complexity of Universal Rigidity

Assuming $(p,\Gamma )$ is not at a conic at infinity and is translated so that its affine span does not include $0$, $(p,\Gamma )$ is UR iff there is no higher rank solution to the SDP than $p$ [2]. Thus, to test for universal rigidity, the main step is to test if there is a feasible solution with rank higher than that of a known input feasible solution $p$ (given say as integers). Numerically speaking, SDP optimization algorithms that use interior point methods produce approximate solutions of the highest possible rank [12, 18] and so in practice one could try such a method to produce a guess about the universal rigidity of $(p,\Gamma )$.

The complexity of getting a definitive answer is a trickier question, even assuming one could reduce the UR question to one of “yes-no” SDP feasibility. In particular, an approximate solution to an SDP optimization problem can be found in polynomial time but the complexity of the SDP feasibility problem remains unknown, even with strict complementarity. See [25] for formal details.

Theorem 1 tells us that for generic inputs, the UR question can be answered by finding the highest rank dual optimal solution. (A framework with integer coordinates will not be generic; however, if the integers are large enough we are likely to avoid all special behavior, as in [15, Sect. 5].) This does not appear to be any help in determining the complexity of testing algorithmically for universal rigidity.