A new visualization scheme of chemical energy density and bonds in molecules

Abstract

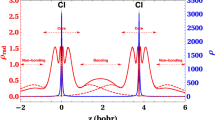
Covalent bond describes electron pairing in between a pair of atoms and molecules. The space is partitioned in mutually disjoint regions by using a new concept of the electronic drop region R _D , atmosphere region R _A , and the interface S (Tachibana in J Chem Phys 115:3497–3518, 2001). The covalent bond formation is then characterized by a new concept of the spindle structure. The spindle structure is a geometrical object of a region where principal electronic stress is positive along a line of principal axis of the electronic stress that connects a pair of the R _D s of atoms and molecules. A new energy density partitioning scheme is obtained using the Rigged quantum electrodynamics (QED). The spindle structure of the stress tensor of chemical bond has been disclosed in the course of the covalent bond formation. The chemical energy density visualization scheme is applied to demonstrate the spindle structures of chemical bonds in H₂, C₂H₆, C₂H₄ and C₂H₂ systems.

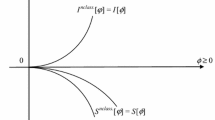
Figure Field theory of the energy density.

Appendix

In the Rigged QED theory, the interaction of a system and its environment is tractable using regional charge and current densities.

Let a system A be embedded in the environment medium M. The corresponding gauge potentials [2] are the regional integrals of the charge and transversal current densities, defined as follows

$$ \hat A_{0_{\text{A}} } (\vec r) = \int\limits_{\text{A}} {{\text{d}}^3 \vec s\frac{{\hat \rho (\vec s)}} {{\left| {\vec r - \vec s} \right|}}} , $$

(100)

$$ \hat A_{0_{\text{M}} } (\vec r) = \int\limits_{\text{M}} {{\text{d}}^3 \vec s\frac{{\hat \rho (\vec s)}} {{\left| {\vec r - \vec s} \right|}}} , $$

(101)

and

$$ \hat {\vec A}_{\text{A}} (\vec r) = \frac{1} {c}\int\limits_{\text{A}} {{\text{d}}^3 \vec s\frac{{\hat {\vec j}_{\text{T}} (\vec s,u)}} {{\left| {\vec r - \vec s} \right|}},} $$

(102)

$$ \hat {\vec A}_{\text{M}} (\vec r) = \frac{1} {c}\int\limits_{\text{M}} {{\text{d}}^3 \vec s\frac{{\hat {\vec j}_{\text{T}} (\vec s,u)}} {{\left| {\vec r - \vec s} \right|}}} , $$

(103)

where the subscript A or M of the integral sign denotes the regional integrals confined to the region A or M, respectively.

Since the regions A and M altogether span the whole space, we have

$$ \hat A_0 (\vec r) = \hat A_{0_{\text{A}} } (\vec r) + \hat A_{0_{\text{M}} } (\vec r), $$

(104)

$$ \hat {\vec A}(\vec r) = \hat {\vec A}_{\text{A}} (\vec r) + \hat {\vec A}_{\text{M}} (\vec r) + \hat {\vec A}_{{\text{radiation}}} (\vec r), $$

(105)

where $\hat {\vec A}_{{\text{radiation}}} (\vec r)$ denotes that portion of the radiation field.

The electric field $\hat {\vec E}(\vec r)$ is decomposed into the electric displacement $\hat {\vec D}(\vec r)$ of the medium M and the polarization $\hat {\vec P}(\vec r)$ of the system A, defined, respectively, as

$$ \hat {\vec D}(\vec r) = - {\text{grad}}\hat A_{0_{\text{M}} } (\vec r) - \frac{1} {c}\frac{\partial } {{\partial t}}\hat {\vec A}_{\text{M}} (\vec r), $$

(106)

$$ \hat {\vec P}(\vec r) = \frac{1} {{4\pi }}{\text{grad}}\hat A_{0_{\text{A}} } (\vec r) + \frac{1} {{4\pi c}}\frac{\partial } {{\partial t}}\hat {\vec A}_{\text{A}} (\vec r), $$

(107)

so that we have

$$ \hat {\vec E}(\vec r) = - {\text{grad}}\hat A_0 (\vec r) - \frac{1} {c}\frac{\partial } {{\partial t}}\hat {\vec A}(\vec r) = \hat {\vec D}(\vec r) - 4\pi \hat {\vec P}(\vec r) - \frac{1} {c}\frac{\partial } {{\partial t}}\hat {\vec A}_{{\text{radiation}}} (\vec r). $$

(108)

Likewise, let the magnetic field $\hat {\vec H}(\vec r)$ of the medium M and the magnetization $\hat {\vec M}(\vec r)$ of the system A be defined, respectively, as

$$ \hat {\vec H}(\vec r) = {\text{rot}}\hat {\vec A}_{\text{M}} (\vec r), $$

(109)

$$ \hat {\vec M}(\vec r) = \frac{1} {{4\pi }}{\text{rot}}\hat {\vec A}_{\text{A}} (\vec r), $$

(110)

then we have

$$ \hat {\vec B}(\vec r) = {\text{rot}}\hat {\vec A}(\vec r) = \hat {\vec H}(\vec r) + 4\pi \hat {\vec M}(\vec r) + {\text{rot}}\hat {\vec A}_{{\text{radiation}}} (\vec r). $$

(111)

The regional charge densities are then represented, respectively, as

$$ \hat \rho _{\text{A}} (\vec r) = - \frac{1} {{4\pi }}\Delta \hat A_{0_{\text{A}} } (\vec r), $$

(112)

$$ \hat \rho _{\text{M}} (\vec r) = - \frac{1} {{4\pi }}\Delta \hat A_{0_{\text{M}} } (\vec r), $$

(113)

and hence

$$ \hat \rho (\vec r) = \hat \rho _{\text{A}} (\vec r) + \hat \rho _{\text{M}} (\vec r). $$

(114)

Likewise, the regional current densities are represented as

$$ \hat {\vec j}_{\text{A}} (\vec r) = \frac{c} {{4\pi }}\left( {\frac{1} {c}{\text{grad}}\frac{\partial } {{\partial t}}\hat A_{0_{\text{A}} } (\vec r) + \square \hat {\vec A}_{\text{A}} (\vec r)} \right) = \frac{\partial } {{\partial t}}\hat {\vec P}(\vec r) + c{\text{rot}}\hat {\vec M}(\vec r), $$

(115)

$$ \hat {\vec j}_{\text{M}} (\vec r) = \frac{c} {{4\pi }}\left( {\frac{1} {c}{\text{grad}}\frac{\partial } {{\partial t}}\hat A_{0_{\text{M}} } (\vec r) + \square \hat {\vec A}_{\text{M}} (\vec r)} \right), $$

(116)

and hence

$$ \hat {\vec j}(\vec r) = \hat {\vec j}_{\text{A}} (\vec r) + \hat {\vec j}_{\text{M}} (\vec r) = \frac{\partial } {{\partial t}}\hat {\vec P}(\vec r) + c{\text{rot}}\hat {\vec M}(\vec r) + \hat {\vec j}_{\text{M}} (\vec r). $$

(117)

The regional decomposition of the longitudinal and transversal components of the current densities are represented as follows

$$ \hat {\vec j}(\vec r) = \hat {\vec j}_{\text{L}} (\vec r) + \hat {\vec j}_{\text{T}} (\vec r), $$

(118)

with

$$ \hat {\vec j}_{\text{L}} (\vec r) = \hat {\vec j}_{{\text{L}}_{\text{A}} } (\vec r) + \hat {\vec j}_{{\text{L}}_{\text{M}} } (\vec r), $$

(119)

$$ \hat {\vec j}_{\text{T}} (\vec r) = \hat {\vec j}_{{\text{T}}_{\text{A}} } (\vec r) + \hat {\vec j}_{{\text{T}}_{\text{M}} } (\vec r), $$

(120)

where

$$ \hat {\vec j}_{{\text{L}}_{\text{A}} } (\vec r) = \frac{c} {{4\pi }} \cdot \frac{1} {c}{\text{grad}}\frac{\partial } {{\partial t}}\hat A_{0_{\text{A}} } (\vec r), $$

(121)

$$ \hat {\vec j}_{{\text{L}}_{\text{M}} } (\vec r) = \frac{c} {{4\pi }} \cdot \frac{1} {c}{\text{grad}}\frac{\partial } {{\partial t}}\hat A_{\text{M}} (\vec r), $$

(122)

$$ \hat {\vec j}_{{\text{T}}_{\text{A}} } (\vec r) = \frac{c} {{4\pi }} \cdot \square \hat {\vec A}_{\text{A}} (\vec r), $$

(123)

$$ \hat {\vec j}_{{\text{T}}_{\text{M}} } (\vec r) = \frac{c} {{4\pi }} \cdot \square \hat {\vec A}_{\text{M}} (\vec r). $$

(124)

Using Eqs. 121, 122, 123 and 124, we have the alternative forms of Eqs. 16 and 17, respectively, as

$$ \hat {\vec j}_{\text{A}} (\vec r) = \hat {\vec j}_{{\text{L}}_{\text{A}} } (\vec r) + \hat {\vec j}_{{\text{T}}_{\text{A}} } (\vec r), $$

(125)

$$ \hat {\vec j}_{\text{M}} (\vec r) = \hat {\vec j}_{{\text{L}}_{\text{M}} } (\vec r) + \hat {\vec j}_{{\text{T}}_{\text{M}} } (\vec r). $$

(126)

The linear response properties of the system A under the interaction with the environment medium M may formally be represented with obvious notation as follows

$$ \hat {\vec D}(\vec r) = \left( {1 + 4\pi \hat {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\chi }} _{\text{e}} (\vec r)} \right)\hat {\vec E}(\vec r) = \hat {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\varepsilon }} (\vec r)\hat {\vec E}(\vec r), $$

(127)

$$ \hat {\vec B}(\vec r) = \left( {1 + 4\pi \hat {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\chi }} _m (\vec r)} \right)\hat {\vec H}(\vec r) = \hat {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\mu }} (\vec r)\hat {\vec H}(\vec r), $$

(128)

$$ \hat {\vec j}(\vec r) = \hat {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {G}} (\vec r)\hat {\vec E}(\vec r). $$

(129)