Abstract
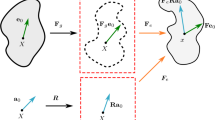
In this paper, a hyperelastic and thermodynamically consistent model for soft tissue is developed that is able to describe the change of the initial orientation of the collagen fibres. Full numerical implementation is considered as well. The collagen architecture is assumed to reorient driven by a specific thermodynamical force. The anisotropy is described by a strain energy function, which is decomposed into a part related to the matrix and a part related to the fibres. The initial fibre orientation is defined by a structural tensor, while the current orientation is described by a time-dependent structural tensor, which results from the initial one by a rotational transformation. The rotation tensor is obtained via an integration process of a rate tensor, which depends on an adequately defined thermodynamical force. The integration is achieved via an exponential map algorithm, where it is shown that the rotation is necessarily a two-parametric one. Efficiency of the proposed formulation is demonstrated using some numerical examples.
Similar content being viewed by others
References
Choquet-Bruhat Y, DeWitt-Morette C, Dillard-Bleick M (1982) Analysis, manifolds and physics part I. North-Holland, Amsterdam
Driessen NJB, Peters GWM, Huyghe JM, Bouten CVC, Baaijens FPT (2003) Remodelling of continuously distributed collagen fibres in soft connective tissues. J Biomech 36: 1151–1158
Driessen NJB, Wilson W, Bouten CVC, Baaijens FPT (2004) A computational model for collagen fiber remodelling in the arterial wall. J Theor Biol 226: 53–64
Dubrovin B, Fomenko A, Novikov S (1984) Modern geometry-methods and applications i. Springer, New York
Eterovic AL, Bathe K-J (1990) A hyperelastic-based large strain elasto-plastic constitutive formulation with combined isotropic-kinematic hardening using the logaritmic stress and strain measures. Int J Num Meth Eng 30: 1099–1114
Flory PJ (1961) Thermodynamic relations for highly elastic materials. Trans Faraday Soc 57: 829–838
Fung YC (1993) Biomechanics—mechanical properties of living tissues. Springer, Berlin
Gasser TC, Ogden RW, Holzapfel GA (2006) Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. J R Soc Interface 3: 15–35
Hariton I, deBotton G, Gasser TC, Holzapfel GA (2007) Stress-driven collagen fiber remodelling in arterial walls. Biomechan Model Mechanobiol 6: 163–175
Holzapfel GA, Ogden RW (2003) Biomechanics of soft tissue in cardiovascular systems, vol. 441. CISM Courses and Lectures. Springer, Heidelberg
Holzapfel GA, Weizsäcker HW (1998) Biomechanical behaviour of the arterial wall and its numerical characterization. Comput Biol Med 27: 377–392
Holzapfel GA, Gasser TC, Ogden RW (2000) A new constitutive framework for arterial wall mechanics and a comparative study of material models. J Elast 61: 1–48
Humphrey JD (2002) Cardiovascular solid mechanics. Springer, Berlin
Humphrey JD, Rajagopal KR (2002) A constrained mixture model for growth and remodeling of soft tissues. Math Methods Mod Appl Sci 12: 407–430
Klinkel S, Sansour C, Wagner W (2005) An anisotropic finite elastic-plastic model for fibre-matrix materials. Comput Mech 35: 409–417
Kuhl E, Garikipati K, Arruda EM, Grosh K (2005) Remodeling of biological tissue: mechanically induced reorintation of a transversely isotropic chain network. J Mech Phys Solids 53: 1552–1573
Menzel A (2007) A fibre reorientation model for orthotropic multiplicative growth configurational driving stresses, kinematics-based reorientation, and algorithmic aspects. Biomech Modeling Mechanobiol 6: 303–320
Nedjar B (2007) An anisotropic viscoelastic fibrematrix model at finite strains: Continuum formulation and computational aspects computer. Comput Methods Appl Mech Eng 196: 1745–1756
Ogden RW (1978) Nearly isochoric elastic deformations: application to rubberlike solids. J Mech Phys Solids 26: 37–57
Rachev A (2003) Remodeling of arteries in response to changes in their mechanical environment. In: Holzapfel GA, Ogden RW (eds.) In 441 CISM course and lectures: Biomechanics of soft tissue in cardiovascular systems, pp 221–273
Sansour C, Kollmann FG (1998) Large viscoplastic deformation of shells. Theory and finite element formulation. Comput Mech 21: 512–525
Sansour C, Wagner W (2001) A model of finite strain viscoplasticity based on unified constitutive equations. Theoretical and computational considerations with applications to shells. Comp Meth Appl Mech Eng 191: 423–450
Schulze-Bauer CAJ, Auer M, Holzapfel GA (2003) Passive biaxial mechanical response of aged human iliac arteries. J Bioemch Eng 125: 395–406
Treloar LRG (1975) The physics of rubber elasticity, 3rd edn. Clarendon Press, Oxford
Zulliger MA, Fridez P, Hayashi K, Stergiopulos N (2004) A strain energy function for arteries accounting for wall composition and structure. J Biomech 37: 989–1000
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Karšaj, I., Sansour, C. & Sorić, J. The modelling of fibre reorientation in soft tissue. Biomech Model Mechanobiol 8, 359–370 (2009). https://doi.org/10.1007/s10237-008-0142-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10237-008-0142-1